Anti-Fatigue Design for Powered Roof Supports Volume 1 - Issue 4

Tadeusz Łagoda¹*, Monika Polak-Micewicz²

• ¹Faculty of Mechanical Engineering, Department of Mechanics and Machine Design, Opole University of Technology, Poland
• ²Famur Institute, Katowice, Poland

Received: March 18, 2021   Published: March 26, 2021

Corresponding author: Tadeusz Łagoda, Faculty of Mechanical Engineering, Department of Mechanics and Machine Design, Opole University of Technology, Poland

DOI: 10.32474/JOMME.2021.01.000119

 

Abstract PDF

Abstract

A powered roof support is defined a set of support sections arranged next to each other, which creates space for mining and transportation machines and also for staff. The housing protects the newly discovered ceiling by moving a distance equal to the width of the mining body. The powered roof supports (PRS) must keep roof in variable cycle loads in mine and then it can lead to a complex combination of physical occurrences and changes in the construction. Micro-damages arising as a result of cyclical loads gradually develop and accumulate, leading to fatigue cracking. This paper presents an approach for the complexity of powered roof supports design taking into account fatigue life. In the work there can also be found some information on existing notches and how they are taken into account in the calculation. The main purpose of the work was to develop such an anti-fatigue design methodology to make calculations using the elastic model, and then at critical points apply the local elastic-plastic model methods using the Neuber model. Next there were adopted the appropriate fatigue criteria to determine fatigue life wall housing. To obtain the final form of the algorithm in this paper there are different fatigue tests presented, including: tests of wall casings with strain gauges and numerical analyzes using finite element method. Based on the tested main subassemblies of the PRS, the most effective method was defined taking into account the average values of cycle amplitudes, and the next step determined the degree of damage for all load supports. The results from experiments allow determining durability of critical places for the main subassemblies of the PRS and determining the most stressed components. Due to the shortage of systematic procedures and guidelines for the strength calculations of PRS enclosure which would take into account fatigue life, the proposed method meets the expectations of a correct and full recognition of static and fatigue strength analyzes.

Keywords: Life-Time; S-N Curve; Stress Concertation; FEM

Introduction

The movement of a powered roof support section behind the progressing coalface results in a cyclical change of its load. During each technological cycle in the wall we can discern the following stages of load: expanding, propping the load from the rock mass, caving. This cycle is repeated during coal mining, which leads to variable stresses in the powered roof support structure. It should be remembered that caving occurs behind the roof support, i.e. the collapse of rocks, which may also cause the appearance of dynamic effects on the anti-collapse support, which is omitted during laboratory tests. The fatigue strength of roof support components should be determined at the design stage, as they are not expected to be replaced during their lifetime inside a mine. It is therefore necessary to correctly estimate the number of cycles beyond which damage may occur in the stress concentration area of a given roof support component. The basic legal instruments ensuring safety are directives and standards: European (EN 1804- 1:2001+A1:2011), American (CONSOL method) or Russian (GOST R 52152-2003), which describe in detail the testing plan, including loads and number of fatigue cycles, which are carried out at a test stand in an accredited certification laboratory.
Fatigue testing of the prototype section of the longwall powered roof support is mainly based on laboratory tests. Nowadays, tendencies among domestic clients are observed to increase the number of cycles up to 60,000 cycles. After testing according to a European standard, the number of cycles for each support block is proportionally increased to reach the expected number of cycles. Bench tests allow to recognize the mechanism of crack formation and precisely determine the durability of the structure, therefore the measurement data from strain gauges are recorded, thus enabling to recognize the nature of strain in the predicted area of crack initiation. The most popular and simplest approach to determining the fatigue limit is to know the dependence of stress amplitude on the number of cycles, so called Wöhler’s or Basquin’s diagram. However, relying solely on these diagrams in the case of the powered roof support is a very large simplification, which omits, among other things, geometric notches, structural notches and average values of cycles. A literature review on multiaxial cyclic fatigue shows that there is no single universal stress criterion for different load conditions. Therefore, one of the main objectives of this work is to attempt durability assessment using numerical analysis based on the finite element method and to adopt an appropriate fatigue criterion in order to determine the most exposed area on this basis, while at the same time identifying the component most exposed to potential failure.

Characteristics of powered roof support tests

Experimental research on the powered roof support was carried out in the Technical Laboratory in Opava (Figure 1) and lasted until the moment of visible damage to the structure. The appearance of cracks threatening the safety of continued testing resulted in stopping the tests and the final determination of the durability. The research method was presented in the works [1 - 9], and the applied criterion of multi-axial fatigue was described in the work [10]. It should be emphasized that although laboratory tests do not fully reflect the actual conditions in the mine underground, the variety of supporting actions and the number of cycles in the stress tests usually exceeds the actual operation of the powered roof support. Such a conclusion was reached after long-term observations of the powered roof support during its examination, operation and servicing.
The results obtained from experimental studies were used to determine elastic and elastic-plastic strain according to the formula below:

Results

The vegetation diversity and ecological spectrum of rare plant species

Post-industrial particular post-mineral exploitation sites, especially those subjected to spontaneous succession are characterized by specific habitat conditions, and thus unique biocoenoses arise on those habitats [18]. They are often characterized by a high number of species (biodiversity). Over 500 plant species were recorded on the post-coal mine heaps and sedimentation [18, 23-25]. Apart from the post-coal mine sites the vascular plant species flora of quarries, gravel and sand pits, post coal-mine heaps and dumps present high floristic richness, including the occurrence of rare and endangered species.
The long term study on the conditions influencing of the diversity of spontaneous vegetation on post coal-mine heaps in Upper Silesia have shown that vegetation diversity is changing in time. The spontaneous vegetation is most diverse in the initial stages of post-coal mine heaps ecosystem development (Figure 1).

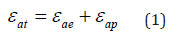
where:
ε_at - amplitude of total strain,
ε_ae - amplitude of elastic strain,
ε_ap - amplitude of plastic strain.
In the cycle of alternating stresses sinusoidally one can distinguish: maximum stresses of the cycle σ_max, minimum stresses of the cycle σ_min, stress amplitude σ_a, average stress of the cycle σ_m, stress change interval T or frequency f. Each stress amplitude σ_a or maximum stress σmax shall be matched by the number of destructive cycles Nf until the stress amplitude σ_a drops to the fatigue limit at the specified number of Nf.
In the first step, from the Ramberg-Osgood equation, the curve of cyclic strain is determined:

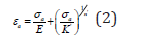
where:
E- Young’s modulus,
σ_a –stress amplitude,
K’ - the coefficient of cyclic strain hardening,
n’ - the exponent of cyclic strain hardening.
The next step is to determine the extremes of the function waveforms for a given type of supporting action, followed by stress amplitudes and mean values according to the following formula:
- stress amplitude σ_a

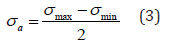
- average value σ_m

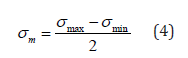
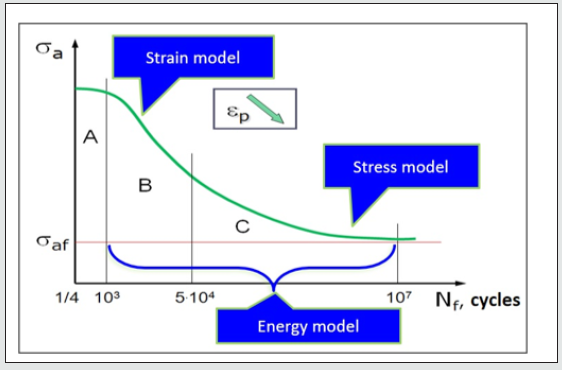
Based on the characteristics prepared from Basquin correlation and material data, the fatigue limit with respect to the crack area can be most easily determined. Thus, three areas can be distinguished depending on stress levels and number of cycles: quasi-static, low cycle (LCF) and high cycle (HCF), for which appropriate multi-axial fatigue criteria are used: strain, stress and energy model combining the two previously mentioned factors (Figure 2).

It should be remembered that there are no clearly defined boundaries between quasi-static and low cycle or low cycle and high cycle strength. Experience shows that the first cracks may occur primarily in the weld areas [11] and that these places should be properly designed using available tools such as numerical programs (e.g. ANSYS, ABAQUS), Welding Institute guidelines [12], or British standards describing permissible fatigue stresses in welded joints [13].
Welded joints are classified as notched elements. Their evaluation is hindered not only by the local geometry but also by the microstructure and residual stresses caused by the welding process[10]. The methods used to estimate the durability of notched elements, and welded joints undoubtedly belong to notched elements, can be divided into local and non-local (global). Both methods can be further divided into those based on stress using the elastic body material model and those using the elasticplastic body model dependencies. When considering the initiation of fracture, it is most often assumed that the initiation takes place at the notch surface. At this point, local stress usually takes on high values and calculated durability often indicates significantly fewer cycles to failure [14, 15]. Global methods most often use the fatigue factor of notch effect K_f whose dependence is based on fatigue characteristics determined in laboratory tests.
For welded joints, the average stress value can be considered to have no significant effect on fatigue life. Łagoda in the work [16] presents the results of welded joint tests. They produced practically identical fatigue diagrams for symmetrical and pulsating loads. This is probably due to the existing high residual stresses. Fatigue strength is relatively slightly dependent on the type of welded joint being analyzed, but is more affected by the type of load, the quality of the weld and its size.
One of many methods of determining the durability of notched elements is to determine the theoretical factor of notch effect K_f (αk - according to Polish literature). This parameter is based on the stress or strain at points of the concentration of stress or strain.

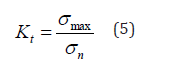
where:
σ_max, ε_max - maximum stress or strain in the notch,
σ_n, ε_n - nominal stress or strain.
If elastic-plastic strain is present in the notch, the Kt factor shall be determined as the geometric mean according to the Neuber rule by means of factors of stress and strain concentration.

while e p max ε − and e p max σ − are the local maximum elastic-plastic strain and the normal stress in the elastic-plastic model respectively [16]. In order to estimate the fatigue life of components containing both geometric and structural notches, methods based on the fatigue coefficient of notch effect Kf can be used, the value of which can be determined from the correlation:

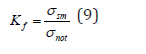
where:
σ_sm - amplitude of nominal stresses in elements without geometric notch,
σ_not - amplitude of nominal stresses in notched elements.

On the basis of fatigue tests carried out for medium strength steels such as S355N, Biłous in the paper [17] proved that for the range of a large number of cycles these steels weaken, and highstrength steels (e.g. S690Q) tend to strengthen with the increasing number of cycles. This conclusion can have a significant impact on the design and selection of the welded joint, especially in the area of the leg pockets.

Example of fatigue life assessment of roof supports

To determine the fatigue life, the degree of failure must be calculated using one of the many damage accumulation hypotheses. In this paper, Palmgren-Miner linear rule [18] was applied, in which it was assumed that each fatigue cycle with specified parameters gives failure equal to the inverse of the total number of cycles causing failure. This function can be written in the form:

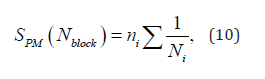
where:
- N_i is the number of cycles for subsequent supporting actions,
- n_i is the number of repetitions of tests for subsequent supporting actions.
According to this hypothesis, damage occurs when the total portions of damage reaches the value of 1.
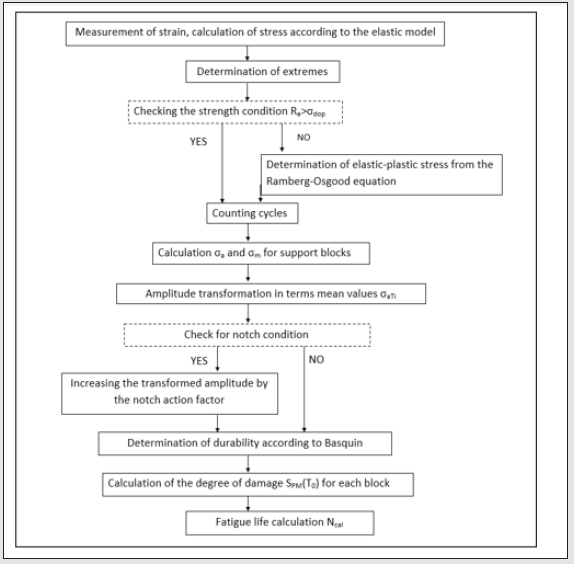
The following is a general algorithm [19] for fatigue life determination using Basquin characteristics (Figure 3).

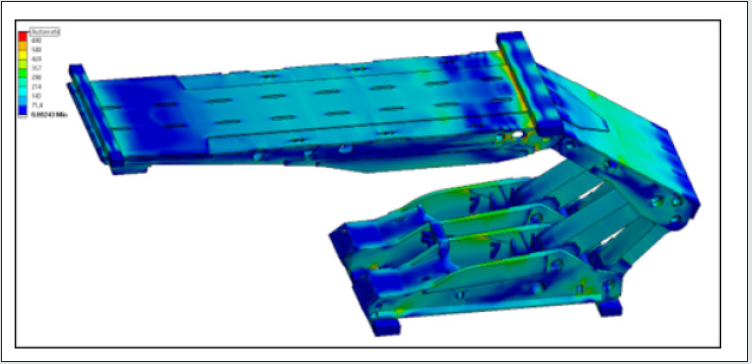
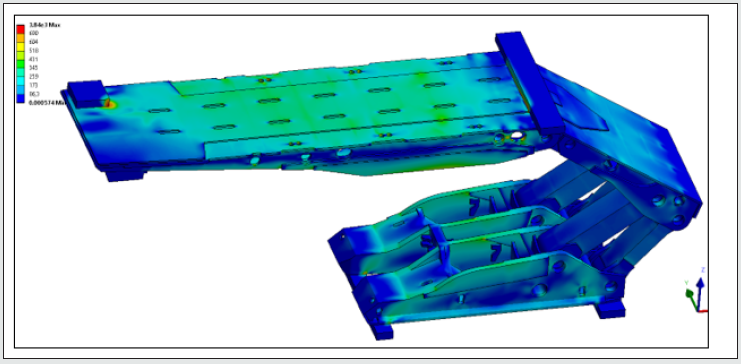
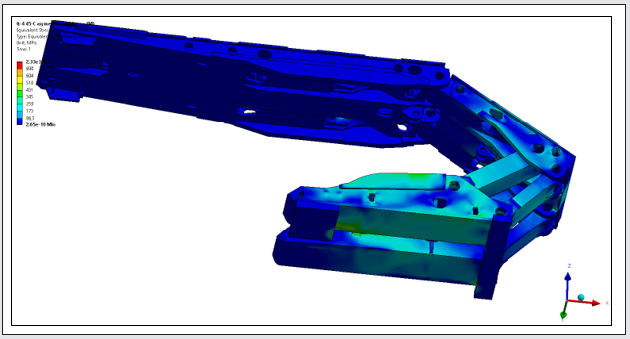
The calculation of effective support stresses, especially in the areas of welded joints, requires the use of FEM. In previous works [20], calculations were carried out for individual structural elements. An attempt was made to determine fatigue life based on the FEM results of the structure as a whole, with appropriate contact points and coefficients of friction between the bending loading blocks (Figures 4 - 6).

Simulation tests carried out on all types of propping actions for the standard prototype roof support in the laboratory showed that the designed structure will last more than 100,000 cycles. Calculated life values showed that the design would meet the high fatigue strength requirements for an increased number of cycles, and that local cracks may occur due to other factors unrelated to the manufacture of the powered roof support.

Conclusion

The presented method and conclusions resulting from the simulation calculations are only a fragment of a complex methodology of predicting the durability of a longwall powered roof support. The strength analyses are continuously modified on the basis of further laboratory tests in order to be able to precisely determine the degree of damage in the individual areas of the structure in the future and to optimize them.
Determination of critical points of the components of powered roof support section and further determination of fatigue life may constitute a significant step towards the development of a methodology for tailoring a longwall roof support according to the client’s requirements and for increasingly difficult mining and geological conditions in which it will be used. It may also allow not only to update the methodology of roof support selection in Poland, in line with the development of knowledge and tools currently available in the world, but may also be a step ahead of the solutions existing in the best scientific and research centers worldwide concerning the selection and reliability for powered roof supports.

References

1. Jaszczuk M, Markowicz J, Szweda S (2009) Ocena wytężenia elementów podstawowych sekcji obudowy zmechanizowanej przy różnym sposobie jej obciążenia, Komtech, Innowacyjne, bezpieczne oraz efektywne techniki i technologie dla górnictwa człowiek - maszyna - środowisko, Gliwice, pp. 347-355.
2. Okrajni J, Plaza M, Markowicz J (2010) Opis procesu odkształcenia elementów obudowy zmechanizowanej, XXIII Sympozjum Zmęczenie i Mechanika Pękania, Bydgoszcz-Pieczyska, pp. 351-352.
3. Hussein MA, Ibrahim AR, Imbaby SS (2013) Load calculations and selection of the powered support basedon rock mass classification and other formulae for Abu-Tartur longwall phosphate mining conditions, Journal of Engineering Science 41(4): 1728 – 1742.
4. Jesiulek D (2019) Monitoring the operational parameters of a power roof support. Journal of Machine Construction and Maintenance pp.109-115.
5. Yetkin ME, Simsir F, Ozfirat MK, Ozffirat PM, Yenice H (2016) A fuzzy approach to selecting supports in longwall mining. South Africa Journal of Industrial Engineering 27(1): 162-177.
6. Rajwa S, Janoszek T, Prusek S (2019) Influence of canopy ratio of powered roof support on longwall working stability – A case study. Int J of Mining Science and Technology 29(4): 591-598.
7. Kumar C(2014) Behavior of shield support in longwall mining, National Institute of Technology, Rourkela, India p. 56.
8. Szurgacz D, Brodny J (2019) Application of a roof support monitoring system for analysis of work parameters of a powered longwall system. E3S Web of Conferences 105: 1-7.
9. Michalak M (2007) Modelling of powered roof support work. Int J of Environmental and Ecological Engineering 5: 603-608.
10. Michalak M (2014) Gradual-randomized model of powered roof supports working cycle, Computer Science and Information Technology, Eds. NMeghanathan et al. p.15-24.
11. Polak- Micewicz M, Łagoda T, Khair Abdul W (2012) Determination of the Strength of Powered Roof Supports According for Fatigue Life. USA – 31st International Conference on Ground Control in Mining, West Virginia University, United States.
12. Łagoda T (2008) Lifetime estimation of welded joint. Springer.
13. Savaidis G, Vormwald(2000) MHot-spot stress evaluation of fatigue in welded structural connections supported by finite element analysis. Int J Fatigue 22(2): 85-91.
14. Łukasik T, Szubryt M (2008) Wytrzymałość zmęczeniowa konstrukcji spawanych - metody nowego podejścia, Materiały szkoleniowe, Instytut spawalnictwa, Gliwice 52(1): 1-5.
15. (1959) BS 7608:2014+A1:2015, Code of practice for fatigue design and assessment of steel structures Peterson R.E., in “Metal Fatigue”, Ed.G.Sines, Mc Grawe-Hill pp.293-306.
16. Weixing Y, Kaiquan X, Yi G (1995) On the fatigue notch factor, Kf. Int J Fatigu 17(4): 245-251.
17. Łagoda T, Biłous P, Blacha Ł (2017) Investigation on the effect of geometric and structural notch on the fatigue notch factor in steel welded joints. Int J Fatigue 101(part II): 224-231.
18. Biłous P, Łagoda T (2009) Structural notch effect in steel welded joints, Materials and design 30: 4562-4564.
19. Palmgren A (1924) Die Lebensdauer Von Kugellagern. VDI-Z 68: 339-341.
20. Polak-Micewicz (2012) Łagoda T.: Szacowanie trwałości zmęczeniowej obudowy ścianowej Fazos. Modelowanie Inżynierskie pp. 237-244
21. Polak-Micewicz M, Łagoda T, (2014) Trwałość zmęczeniowa zmechanizowanych obudów górniczych, Wieloosiowe zmęczenie losowe elementów maszyn i konstrukcji, Część XVI, Studia i Monografie z. 376, Opole,poland.