Neuroimaging Contributions to the Understanding of Neuropsychological Cognitive Processing for Numeracy and Mathematics Volume 3 - Issue 4

John Gountas¹* and Marcela Moraes²

• ¹Department of neurology, Notre Dame University, Australia
• ²Department of neurology, Curtin University of Technology, Australia

Received: January 06, 2020;   Published: January 22, 2020

Corresponding author: John Gountas, Department of neurology, Notre Dame University, Fremantle, WA, Australia

DOI: 10.32474/SJPBS.2020.03.000166

Abstract PDF

Introduction

Numerical and mathematical processing skills has a long history from the ancient classical Greeks Plato, Aristotle Frank, Mendel [1] to the birth of modern psychology, with John Dewey [2], Conant [3], O’Shea [4], suggesting that children learn numerical concepts by reinforcement, not in an abstract way, by identifying similarities, differences of empirical individual units, forming general concepts. This essay follows through the recent evolution of neuroimaging studies debate, sets the theoretical context of three dominant theories that influenced the context of research tools/methods; and how neuroscientific research has contributed uniquely to the understanding of numerosity. The essay concludes with a cogent argument that alternative research tools are necessary, complimentary, and multidisciplinary research generates different types/levels of new hypotheses, ensuing more reliable and valid information which benefits individuals, educationalists and society at large. Numerical processing (referring to arithmetic, mathematics, geometry and advanced computation) is huge. The paper is an eclectic review of the neurotypical findings of general numerical processing only but excludes dyscalculia Menon [5].

Numeracy Importance

The overwhelming research suggest that, numeracy is essential for progress in all aspects of life. Understanding numbers is the basis for developing arithmetic and mathematical skills of all levels and types of applications Dehaene [6], Hurford [7]. Major longitudinal research studies in the UK Bynner, Parsons [8], Donato [9], documented the phenotypic and behavioural outcomes of poor numerical skills and highlight the negative consequences on men’s and women’s, employment opportunities, health outcomes, social-civic involvement and overall quality of life Parsons, Banner [10]. Finding out if specific numerical processing is actually an observable brain process or not, is important to make stronger correlational claims, regarding relationships of numerosity and language.

Theories and Neuroimaging

New neuroimaging tools are used to test existing and emerging new theories and collect data that are impossible with surveys, and experiments. However, without multimethod, multiparadigm comparisons to make valid, reliable and nomological evaluations of competing claims Goya, Pitre [11], Hsee [12], Hsee [13], Hagger [14]. Three theoretical strands attempt to explain the development of number processing, using different research approaches. The first theory suggests that language is innate, culturally constructed and absence impedes learning numerical concepts and knowledge Chomsky [15], Hurford [16], Wiese [17], Spelke [18]. Their position without neuroscientific data, is not supported empirically, of how, when, and where language underpins numerical development. The second theory suggests that children learn numerical concepts as part of lexical acquisition and development of Theory of Mind (TOM) Bloom [19], Clark [20-22]. TOM facilitates multiple perspective taking, conceptual differentiation, through social interactions, enabling nuanced meaning differentiation between words, symbols, and number associations. However, Bloom and Clark, provide weak empirical evidence that brain processing occurs this way, and fail to account for alternative hypotheses.

The third theoretical position postulates a biological, evolutionary, ontogenetic Carey [23], innate ability of ‘number sense’ and processed in distinct brain areas Dehaene [24]. Innate, numerical processing is present in all cultures with and without dedicated number words Pica et al., 2004; Lasne [25]. Dehaene and co-researchers, Dehaene [26], Dehaene & Cohen [27], Dehaene [28] using neuroimaging data proposed that different numerical formats are processed in different brain regions. First, visual Arabic numbers are processed by bilateral activity in inferior ventral occipito-temporal areas; secondly, the inferior parietal areas process analogical size, and approximate volume; and thirdly, word numbers are processed in the left perisylvian areas Dehaene [29]. Dehaene and colleagues, during a period of 20 years, carried out extensive neuroscientific research to disentangle the effects of language-dominant or spatial iconic representation of numerical processing and whether there are specific brain regions innately dedicated to non-verbal numerical processing Dehaene [29], Dehaene [28], Pica et al., 2004; Agrillo [30], Lasne [25].

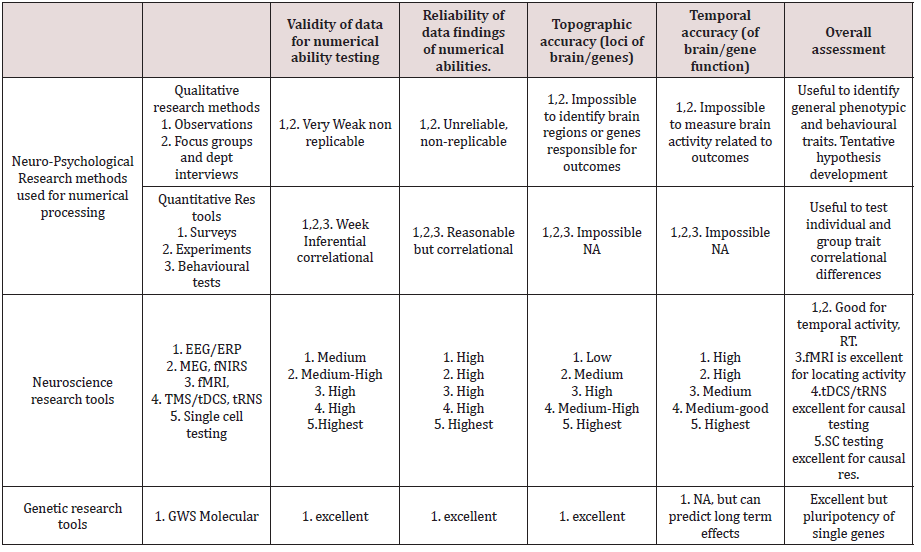
They claim that, innate numerical ability theory is evolutionary Dehaene [28] Pica et al., 2004, and studied systematically using different tasks to understand the conceptual processes of numerical approximation, estimation, and manipulation related to concrete examples, in non-numerically literate (Amazonian Munduruku tribe) and literate western cultures McCrink [31]. To support their theory, that numbers are language-independent representations, Dehaene and colleagues, focused on the dedicated biological brain networks, which are putatively responsible for basic number processing. Their multimethod research produced diverse but supporting evidence of evolutionary innate abilities in animals, infants and adult humans, independent of other abilities. Their neuroscientific research using a range of neuroscientific tools, fMRI, MEG, EEG, and brain legions, suggests that the inferior parietal region is implicated in number processing Dehaene [28]; King & Dehaene, 2014. This level of specificity of explanatory power is only possible with neuroimaging and multimethod approaches. The tripartite model by Dehaene [28] implicating the horizontal segment of IPS, the left AG related to the perisylvian areas, and the bilateral PPS, was further re-tested by Piazza [32], Cohen Kardes [33], using fMRI, fMRA and ERP tools. These multimethod findings have provided convergent validity evidence that the left IPS processes numerical quantities irrespective of format (Arabic, word, and mixed format), but the right IPS processes quantities of Arabic numerals only. Nieder, Jacob [34,35], tested numerical processing of magnitudes and Approximate Number Systems, with primates using single cell-neuron methods and found converging evidence that humans and animals can process numbers without words, but using approximate estimates, activating different populations of neurons bilaterally in the IPS and lateral PFC. Rosenberg-Lee [36], investigated the PPC in detail to identify the specific cytoarchitecture for four calculations (+, -, *, %), and found differences in processing these basic arithmetic tasks by the IPS, SPL and AG. Converging neuroimaging findings using different neuroimaging tools, augment the credibility of prior theoretical positions. Hyde [37], using fNIRS, found that 6 months old babies’ right parietal areas, are specialised for number processing, before language development and that this ability is lateralized with environmental experiences. Artemenko [38] in a longitudinal fNIRS study found that fronto-parietal network brain networks for arithmetic are well established for adolescents. Amalric [39] found that blind mathematicians process advanced mathematics in similar brain networks as sighted without the visual experience. These fine-grained differences of numerical developmental processing, time duration, age differentiation, format presentation (numerals, words), provide new information and new hypotheses, and models which are impossible to test without neuroimaging (Table 1).

Future Directions

The meta-analysis by Arsalidou [40], found that the core brain regions for numerical processing are indeed the parietal regions (IPS and precuneus), the insula, claustrum, the frontal cortex (e.g., superior and medial frontal gyri), and cingulate. However, the developmentally changing networks and the function of typical and atypical brains regarding all interconnected areas (bilateral frontal (DLPFC, VLPFC), parietal (IPS, AG, SMG), occipito-temporal and medial temporal, including HC areas) are not well understood yet, according to Peters and De Smedt [41]. New ways of investigating brain network hubs using resting-state fMRI can fine tune our understanding of numerical connectivity Van Den Heuvel [42].

Educational Implications

The impressive neuroscientific discoveries so far have identified more brain areas and networks involved using, multimethod neuroimaging approaches to discover causal relationships (Amalrick et al., 2018). Glen [43] found that neuroplasticity and active epigenetic input of numerical exposure/talk, can improve and reverse some numerical deficiencies (Michels, et al., 2019). De Muoi, et al., (in press), eye tracking can help educationalists to identify appropriate individualised teaching methods to cope with time pressure. Dillon [44] suggest that developing relevant games to teach children numerical skills, and approximate number systems have positive and long-lasting improvements Khanum [45]. Researchers using tRNS, found improvements in brain connectivity and numerical performance Popescu [46], Pasqualotto [47]. Scientific advances are usually made sequentially Kuhn [48], Lakatos [49], Popper [50]. Investigating genetic, and epigenetics Kovas [51] are essential additions to neuroscientists. Neuroimaging is essential but not sufficient, to achieve nomological validity Hagger [52]. Combining new genetics with neuroscientific research provide more power to advance our understanding and models which can explain provisionally the etiology of genetic and phenotypic numerical behaviours [53,54-75].

References

1. Frank E (1940) The Fundamental Opposition of Plato and Aristotle. The American Journal of Philology 61(2): 166-185.
2. Dewey J (1896) Psychological Review 3(3): 326-329.
3. Conant LL (1896) The Number Concept: Its Origin and Development. Macmillan, New York and London.
4. O'Shea MV (1901) The psychology of number: a genetic view. Psychological Review 8(4): 371-383.
5. Menon V (2016) Working memory in children's math learning and its disruption in dyscalculia. Current Opinion in Behavioral Science 10: 125-132.
6. Dehaene S (1997) The Number Sense: How the Mind Creates Mathematics. Oxford University Press, NY, USA.
7. Hurford JR (1987) Language and Number: The Emergence of a Cognitive System. Blackwell, Oxford, UK.
8. Bynner J, Parsons S (1997) Does Numeracy Matter? Evidence from the National Child Development Study on the Impact of Poor Numeracy on Adult Life. Basic Skills Agency, England, UK.
9. Donati G, Meaburn EL, Dumontheil I (2019) The specificity of associations between cognition and attainment in English, maths and science during adolescence. Learning and Individual Differences 69: 84-93.
10. Bynner J, Parsons S (2006) New Light on Literacy and Numeracy. National Research and Development Centre for Adult Literacy and Numeracy.
11. Gioia DA, Pitre E (1990) Multiparadigm Perspectives on Theory Building. Academy of Management Review 15(4): 584-602.
12. Hsee CK (1996) Attribute Evaluability: Its Implications for Joint-Separate Evaluation Reversals and Beyond. Organizational Behavior and Human Decision Processes 67(3): 247-257.
13. Hsee CK, Loewenstein GF, Blount S, Bazerman MH (1999) Preference reversals between joint and separate evaluation of options: A review and theoretical analysis. Psychological Bulletin 125(5): 576-590.
14. Hagger MS, Giscard DF, Chatzisarantis N (2017) On Nomological Validity and Auxiliary Assumptions: The Importance of Simultaneously Testing Effects in Social Cognitive Theories Applied to Health Behavior and Some Guidelines. Front Psychol8: 1900-1933.
15. Chomsky N (1988) Language and the Problems of Knowledge. MIT Press, Cambridge, Massachusetts, London, England.
16. Wiese H (2003) Numbers, Language, and the Human Mind. Cambridge University Press, Cambridge, England.
17. Spelke ES (2017) Core Knowledge, Language, and Number. Language Learning and Development 13(2): 147-170.
18. Bloom P (2000) How Children Learn the Meanings of Words. MIT Press, Cambridge, England.
19. Clark EV (1990) On the pragmatics of contrast. Journal of Child Language 17: 417-431.
20. Clark EV (1993) The lexicon in acquisition. Cambridge University Press, Cambridge, England.
21. Clark EV (1997) Conceptual perspective and lexical choice in acquisition. Cognition 64(1): 1-37.
22. Carey S (1998) Knowledge of Number: Its Evolution and Ontogeny. Science 282(5389): 641-642.
23. Lasne G, Piazza M, Dehaene S, Kleinschmidt A, Eger E (2019) Discriminability of numerosity-evoked fMRI activity patterns in human intra-parietal cortex reflects behavioral numerical acuity. Cortex 114: 90-101.
24. Dehaene S (1992) Varieties of numerical abilities. Cognition 44(1-2): 1-42.
25. Dehaene S, Cohen L (1995) Towards an anatomical and functional model of number processing. Mathematical Cognition 1: 82-120.
26. Dehaene S, Piazza M, Pniel P, Cohen L (2003) Three Parietal Circuits for Number Processing. Cogn Neuropsychol 20(3): 487-506.
27. Agrillo C, Piffer L, Bisazza A, Butterworth B (2012) Evidence for Two Numerical Systems That Are Similar in Humans and Guppies. PLoS ONE 7(2): e31923.
28. McCrink K, Spelke ES, Dehaene S, Pica P (2012) Non-symbolic halving in an Amazonian indigene group. Dev Sci 16(3): 451-462.
29. Piazza M, Pinel P, Le Bihan D, Dehaene S (2007) A Magnitude Code Common to Numerosities and Number Symbols in Human Intraparietal Cortex. Neuron 53(2): 293-305.
30. Cohen Kadosh R, Cohen Kadosh K, Kaas A, Henik A, Goebel R (2007) Notation-Dependent and -Independent Representations of Numbers in the Parietal Lobes. Neuron 53(2): 307-314.
31. Jacob SN, Valentín D, Nieder A (2012) Relating magnitudes: the brain’s code for proportions. Trends in Cognitive Sciences 16(3): 157-166.
32. Nieder A, Diester I, Tudusciuc O (2006) Temporal and Spatial Enumeration Processes in the Primate Parietal Cortex. Science 313(5792): 1431-1435.
33. Rosenberg Lee M, Chang TT, Young CB, Wu S, Menon V (2011) Functional dissociations between four basic arithmetic operations in the human posterior parietal cortex: A cytoarchitectonic mapping study. Neuropsychologia 49(9): 2592-2608.
34. Hyde DC, Boas DA, Blair C, Carey S (2010) Near-infrared spectroscopy shows right parietal specialization for number in pre-verbal infants. Neuroimage 53(2): 647-52.
35. Artemenko C, Soltanlou M, Ehlis AC, Nuerk HC, Dresler T (2018) The neural correlates of mental arithmetic in adolescents: a longitudinal fins study. Behavioral and Brain Functions 14(1): 1-13.
36. Amalric M, Denghien I, Dehaene S (2018) On the role of visual experience in mathematical development: Evidence from blind mathematicians. Developmental Cognitive Neuroscience 30: 314-323.
37. Arsalidou M, Pawliw Levaca M, Sadeghia M, Pascual Leone J (2018) Brain areas associated with numbers and calculations in children: Meta analyses of fMRI studies. Dev CognNeurosci30: 239-250.
38. Peters L, DeSmedt B (2018) Arithmetic in the developing brain: A review of brain imaging studies. Developmental Cognitive Neuroscience 30: 265-279.
39. Van Den Heuvel MI, Turke E, Manninga JH, Hect J, Hernandez Andrade E, et al. (2018) Hubs in the human fetal brain network. Dev Cogn Neurosci 30: 108-115.
40. Glenn DE, Demir Lira OE, Gibson DJ, Congdon EL, Levine SC (2018) Resilience in mathematics after early brain injury: The roles of parental input and early plasticity. Dev Cogn Neurosci 30: 304-313.
41. Dillon MR, Kannan H, Joshua T, Dean JT, Elizabeth S (2017) Cognitive science in the field: A preschool intervention durably enhances intuitive but not formal mathematics. Science 357(6346): 47-55.
42. Khanum S, Hanif R, Spelke ES, Bartolutti I, Hyde DC (2016) Effects of Non-Symbolic Approximate Number Practice on Symbolic Numerical Abilities in Pakistani Children. PLoS ONE 11(10): e0164436.
43. Adams JW, Barmby P, Mesoudi A (2017) The Nature and Development of Mathematics: Cross Disciplinary Perspectives on Cognition, Learning and Culture. Routledge, London.
44. Amalric M, Dehaene S (2019) A distinct cortical network for mathematical knowledge in the human brain. Neuroimage 189: 19-31.
45. Anobile G, Tomaiuolo F, Campana S, Cicchini GM (2019) Three-systems for visual numerosity: A single case study. Neuropsychology 136: 107-259.
46. Arsalidou M, Taylor MJ (2011) Is 2 + 2 = 4? Meta-analyses of brain areas needed for numbers and calculations. NeuroImage 54(3): 2382-2393.
47. Brewer L (2013) Enhancing youth employability: What? Why? and How? Guide to core work skills: International Labour Organization.
48. Brookman Byrne A, Mareschal D, Tolmie AK, Dumontheil I (2019) The Unique Contributions of Verbal Analogical Reasoning and Nonverbal Matrix Reasoning to Science and Math Problem-Solving in Adolescence. Mind, Brain, and Education 13(3): 211-223.
49. Brookman Byrne A, Mareschal D, Tolmie AK, Dumontheil Iroise (2018) Inhibitory control and counter intuitive science and maths reasoning in adolescence. PLoS One 13(6): 1-19.
50. Butterworth B, Kovas Y (2013) Understanding Neurocognitive Developmental Disorders Can Improve Education for All. Science 340(6130): 300-305.
51. Bynner J, Parsons S (1998) Use it or Lose it? The Basic Skills Agency. London, UK.
52. Campbell JI (1994) Architectures for numerical cognition. Cognition 53: 1-44.
53. Care E, Kim H, Anderson K, Gustafsson Wright E (2017) Skills for a Changing World: National Perspectives and the Global Movement. DC: The Brookings Institution Washington, US.
54. Carey S, Barner D (2019) Ontogenetic Origins of Human Integer Representations. Trends in Cognitive Sciences 23(10): 823-835.
55. Cattell JM (1898) The reaction-time of counting. Psychological Review 5(1): 70-71.
56. Cicchini GM, Anobile G, Burr DC (2019) Spontaneous representation of numerosity in typical and dyscalculic development. Cortex 114: 151-163.
57. Cirino PT, Tolar TD, Fuchs LS, Huston Warren E (2016) Cognitive and numerosity predictors of mathematical skills in middle school. J Exp Child Psychol 145: 95-119.
58. Crollen V, Lazzouni L, Rezk M, Bellemare A, Lepore F, et al. (2019) Recruitment of the occipital cortex by arithmetic processing follows computational bias in the congenitally blind. NeuroImage 186: 549-556.
59. Day M, Boardman MC, Krueger NF (2017) Handbook of Research Methodologies and Design in Neuroentrepreneurship. Edward Elgar Publishing Ltd. Cheltenham, UK.
60. Dehaene S (2011) The Number Sense: How the Mind Creates Mathematics, Revised and Updated Edition. Oxford University Press, NY, USA.
61. De Mooij SMM, Kirkham NZ, Raijmakers M, Van Der Maas HLJ, Dumontheil I (2019) Should online maths learning environments be tailored to individuals’ cognitive profiles? Journal of Experimental Child Psychology 191: 104-220.
62. Harris J, Ciorciari J, Gountas J (2018) Consumer Neuroscience for Marketing Researchers. Journal of Consumer Behavior 17(3): 239-252.
63. Kovas Y, Petrill SA, Plomin R (2007) The Origins of Diverse Domains of Mathematics: Generalist Genes but Specialist Environments. J Educ Psychol 99(1): 128-139.
64. Kuhn TS (1970) The Structure of Scientific Revolutions, Chicago: University of Chicago Press. Second edition, London.
65. Lakatos I (1970) Falsification and the methodology of scientific research programmer. In: Criticism and the Growth of Knowledge, Lakatos I, Musgrave A (Edt.), Cambridge University Press, Cambridge, England.
66. McCloskey M (1992) Cognitive mechanisms in numerical processing: evidence from acquired dyscalculia. Cognition 44(1-2): 107-157.
67. McCrink K, Spelke ES (2016) Non-symbolic division in childhood. JExp Child Psychol142: 66-82.
68. OECD (2016) The Survey of Adult Skills: Reader’s Companion. (2^nd), OECD Skills Studies, OECD Publishing, Paris, France.
69. Pasqualotto A (2016) Transcranial random noise stimulation benefits arithmetic skills. NeurobiolLearn Mem 133: 7-12.
70. Pedro Pinheiro Chagas P, Piazza M, Dehaene S (2019) Decoding the processing stages of mental arithmetic with magnetoencephalography. Cortex 114: 124-139.
71. Popescu T, Krause B, Terhune DB, Twose O, Page T, et al. (2016) Transcranial random noise stimulation mitigates increased difficulty in an arithmetic learning task. Neuropsychologia 81: 255-264.
72. Popper K (2002) The Logic of Scientific Discovery. Routledge, New York, USA.
73. Rotondaro F, Ponticorvo M, Gigliotta O, Pinto M, Pellegrino M, et al. (2019) The Number Interval Position Effect (NIPE) in the mental bisection of numerical intervals might reflect the influence of the decimal-number system on the Gaussian representations of numerosities: A combined developmental and computational-modelling study. Cortex 114: 164-175.
74. Sabates R, Parsons S (2012) The contribution of basic skills to health-related outcomes during adulthood: evidence from the BCS70. Department for Business, Innovation and Skills, London, England.
75. Vandala NG (2019) The transformative effect of correctional education: A global perspective. Cogent Social Sciences 5: 1-15.