Seismic Time Fractal Dimension for Characterizing Shajara Reservoirs of The Permo – Carboniferous Shajara Formation, Saudi Arabia Volume 2 - Issue 1

Khalid Elyas Mohamed Elameen Alkhidir*

• Department of Petroleum and Natural Gas Engineering, college of Engineering, King Saud University, Riyadh, Saudi arabia

Received: July 18, 2018;   Published: July 26, 2018

Corresponding author: Khalid Elyas Mohamed Elameen Alkhidir, Department of Petroleum and Natural Gas Engineering, college of Engineering, King Saud University, Riyadh, Saudi arabia

DOI: 10.32474/MAOPS.2018.02.000128

Abstract PDF

Abstract

The quality and assessment of a reservoir can be documented in detail by the demonstration of seismic time. This research aims to calculate fractal dimension from the relationship among seismic time, maximum seismic time and wetting phase saturation and to approve it by the fractal dimension derived from the relationship among capillary pressure and wetting phase saturation. In this research, porosity was measured on real collected sandstone samples and permeability was calculated theoretically from capillary pressure profile measured by mercury intrusion contaminating the pores of sandstone samples in consideration. Two equations for calculating the fractal dimensions have been employed. The first one defines the functional relationship between wetting phase saturation, seismic time, maximum seismic time and fractal dimension. The second equation involves to the wetting phase saturation as a function of capillary pressure and the fractal dimension. Two procedures for obtaining the fractal dimension have been utilized. The first procedure was done by plotting the logarithm of the ratio between seismic time and maximum seismic time versus logarithm wetting phase saturation. The slope of the first procedure = 3- Df (fractal dimension). The second procedure for obtaining the fractal dimension was determined by plotting the logarithm of capillary pressure versus the logarithm of wetting phase saturation. The slope of the second procedure = Df -3. Based on the obtained results of the fabricated stratigraphic column and the attained values of the fractal dimension, the sandstones of the Shajara reservoirs of the Shajara Formation were divided here into three units. The gained units from bottom to top are: Lower Shajara seismic time Fractal Dimension Unit, Middle Shajara seismic time Fractal dimension Unit, and Upper Shajara seismic time Fractal Dimension Unit. The results show similarity between seismic time fractal dimension and capillary pressure fractal dimension. It was also noted that samples with wide range of pore radius were characterized by high values of fractal dimensions due to an increase in their connectivities. In our case, and as conclusions the higher the fractal dimension, the higher the heterogeneity, the higher the permeability, the better the reservoir characteristics.

Introduction

The wetting phase saturation can be described as function of capillary pressure and fractal dimension was demonstrated by [1]. The Purcell model was found to be the best fit to the experimental data of the wetting phase relative permeability for the cases if the measured capillary pressure curve had the same residual saturation as the relative permeability curve was described by [2]. A theoretical model to correlate capillary pressure and resistivity index based on the fractal scaling theory was reported by [3]. The fractal dimension resulting from longer transverse NMR relaxation times and lower capillary pressure reflects the volume dimension of larger pores was described by [4]. The fractal dimension derived from the short NMR relaxation times is like the fractal dimension of the internal surface was described by [4]. The fractal dimensions can be used to represent the complexity degree and heterogeneity of pore structure, and the coexistence of dissolution pores and large intergranular pores of Donghetang sandstones contributes to a heterogeneous pore throat distribution and a high value of fractal dimension was reported by [5]. The relationship among capillary pressure (PC), nuclear magnetic transverse relaxation time (T2) and resistivity index (I) was studied by [6]. An increase of bubble pressure fractal dimension and pressure head fractal dimension and decreasing pore size distribution index and fitting parameters m*n due to possibility of having interconnected channels was confirmed by [7]. An increase of fractal dimension with increasing arithmetic, geometric relaxation time of induced polarization, permeability and grain size was investigated by [8-10]. An increase of seismo electric and fractal dimensions with increasing permeability and grain size was described by [11].

Materials and Methods

Porosity was measured on collected sandstone samples and permeability was calculated from the measured capillary pressure by mercury intrusion techniques. Two procedures for obtaining the fractal dimension have been developed. The first procedure was completed by plotting the logarithm of the ratio between seismic time and maximum seismic time versus logarithm wetting phase saturation. The slope of the first procedure = 3- Df (fractal dimension). The second procedure for obtaining the fractal dimension was concluded by plotting the logarithm of capillary pressure versus the logarithm of wetting phase saturation. The slope of the second procedure = Df -3.

The seismic time can be scaled as

Sw=[ST/ST_max]^[3-Df] (1)

Where Sw the wetting phase saturation, ST the seismic time in second, ST_max the maximum seismic time in second, and Df the fractal dimension. Equation 1 can be proofed from the frequency dependent filtration velocity

V=[(k*ρ*ω²*U_s)/μ] (2)

Where V the filtration velocity in meter / second, k the permeability in square meter, ρ the fluid density in kilo gram / cubic meter, ω the angular frequency, U_s the seismic displacement in meter, and μ the fluid viscosity in pascal* second.

But; ω=2*π*f (3)

Where f the seismic frequency in second_-1

Insert equation 3 into equation 2

V=[(k*ρ*4*π²*f²*U^s)/μ] (4)

But;f=1/ST (5)

Where ST the seismic time in second

Insert equation 5 into equation 4

V=[(k*ρ*4*π²*U_s)/(μ*〖ST〗²)] (6)

The density ρ can be scaled as

ρ=[(〖reff〗²*C_E)/(8*σ*μ*C_s)] (7)

Where ρ the density in kilo gram / cubic meter, reff the effective pore radius in meter, C_E the electro osmotic coefficient in pascal / volt, σ the fluid conductivity in Siemens / meter, μ the fluid viscosity in pascal * second and C_S the streaming potential coefficient in volt / pascal.

Insert equation 7 into equation 6

If the pore radius r is introduced, equation 8 will become

V=[(k*r²*C_E*4*π²*U_s)/(8*σ*μ*C_S*μ*〖ST〗² )] (9)

Equation 9 after rearranging the pore radius will become

r²=[(V*8*σ*μ*C_S*μ*〖ST〗²)/(k*C_E*4*π²*U_s)] (10)

r_max²=[(V*8*σ*μ*C_S*μ*〖ST〗_max²)/(k*C_E*4*π²*U_s)] (11)

Where ST_max the maximum seismic time

Divide equation 10 by equation 11

[r²/(r_max²)]=[((V*8*σ*μ*C_S*μ*〖ST〗²)/(k*C_E*4*π²*U_s))/((V*8*σ*μ*C_S*μ*〖ST〗_max²)/(k*C_E*4*π²*U_s))] (12)

Equation 12 after simplification will become

[r/r_max]=[ST/〖ST〗_max] (13)

Take the logarithm of equation 13

log[r/r_max]=log〖[ST/〖ST〗_max]〗 (14)

But;log[r/r_max]=logSw/([3-Df]) (15)

Insert equation 15 into equation 14

logSw/([3-Df])=log〖[ST/〖ST〗_max]〗 (16)

Equation 16 after log removal will become

Sw=[ST/〖ST〗_max]^[3-Df] (17)

Equation 17 the proof of equation 1 which relates the water saturation, the seismic time, the maximum seismic time and the fractal dimension.

Results and Discussion

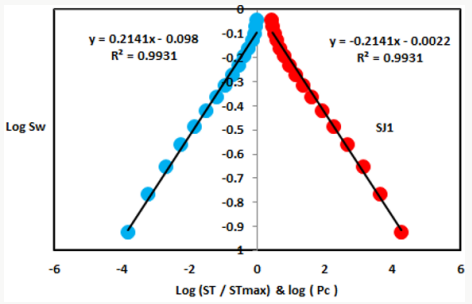
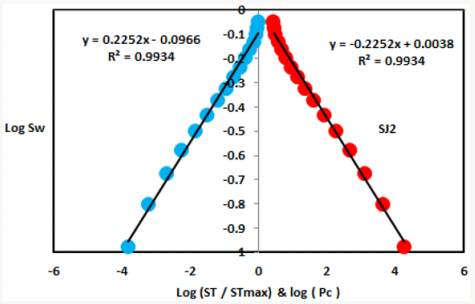
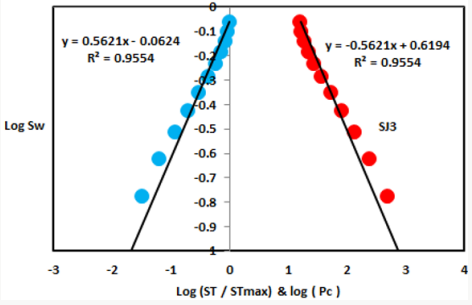
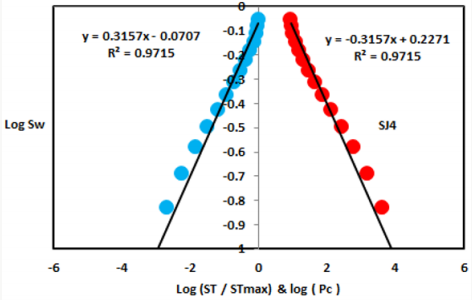
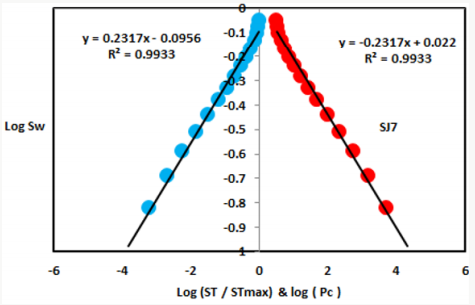
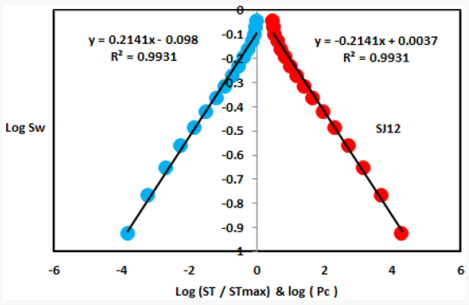
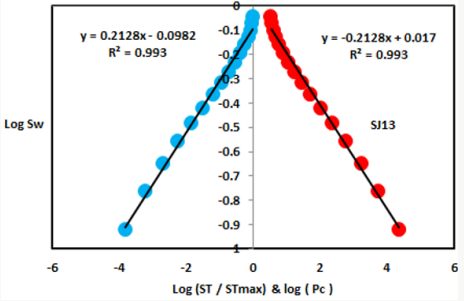
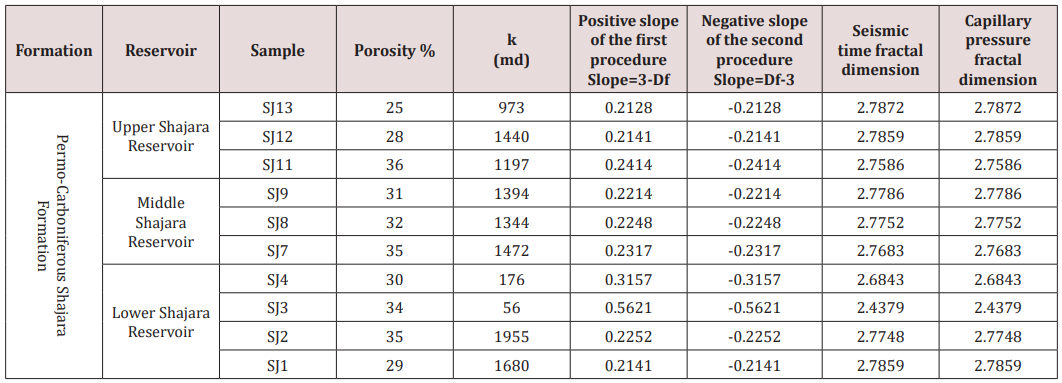
Based on field observation the Shajara Reservoirs of the PermoCarboniferous Shajara Formation were divided here into three units as described in Figure 1. These units from bottom to top are: Lower, Middle, and Upper Shajara Reservoir. Their attained results of the seismic time fractal dimension and capillary pressure fractal dimension are demonstrated in Table 1. Based on the accomplished results it was found that the seismic time fractal dimension is equal to the capillary pressure fractal dimension. The maximum value of the fractal dimension was found to be 2.7872 allocated to sample SJ13 from the Upper Shajara Reservoir as confirmed in Table 1. Whereas the minimum value of the fractal dimension 2.4379 was reported from sample SJ3 from the Lower Shajara reservoir as showed in table 1. The seismic time fractal dimension and capillary pressure fractal dimension were noted to increase with increasing permeability as proofed in Table1 owing to the possibility of having interconnected channels. The Lower Shajara reservoir was represented by six sandstone samples (Figure 1), four of which label as SJ1, SJ2, SJ3 and SJ4 as confirmed in Table1 were nominated for capillary measurements. Their positive slopes of the first procedure (log of the ratio of seismic time to maximum seismic time versus log wetting phase saturation) and negative slopes of the second procedure (log capillary pressure versus log wetting phase saturation are delineated in Figures 2- 5 and Table 1. As we proceed from sample SJ2 to SJ3 a noticeable reduction in permeability due to compaction was reported from 1955 md to 56 md which reflects decrease in seismic time fractal dimension from 2.7748 to 2.4379 as identified in Table 1. Again, an increase in grain size and permeability was proved from sample SJ4 whose seismic time fractal dimension and capillary pressure fractal dimension was found to be 2.6843 as described in Table 1.

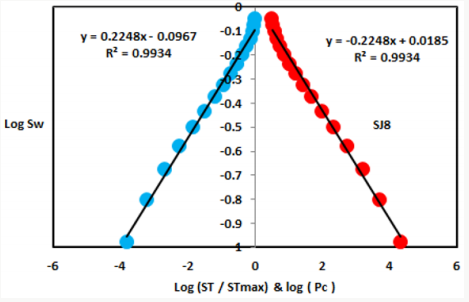
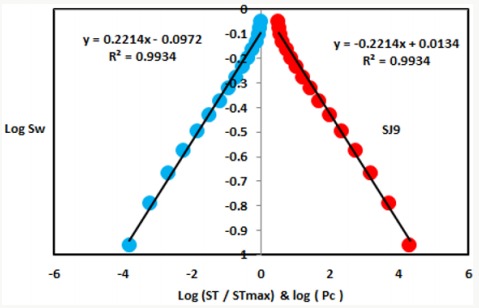
In contrast, the Middle Shajara reservoir which is separated from the Lower Shajara reservoir by an unconformity surface as shown in Figure 1. It was designated by four sandstone samples (Figure 1), three of which namely SJ7, SJ8, and SJ9 as clarified in Table1 were preferred to perform capillary pressure measurements. Their positive slopes of the first procedure and negative slopes of the second procedure are shown in Figures 6-8 and Table 1. Moreover, their seismic time fractal dimensions and capillary pressure fractal dimensions show similarities as delineated in Table 1. Their fractal dimension values are higher than those of samples SJ3 and SJ4 from the Lower Shajara Reservoir due to an increase in their permeability as described in Table 1.

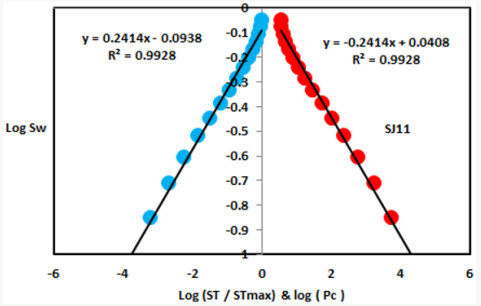
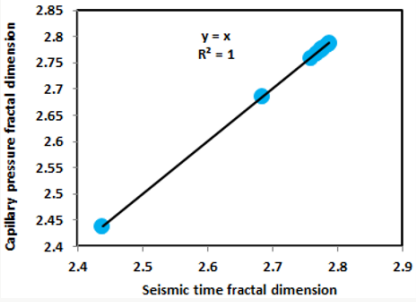
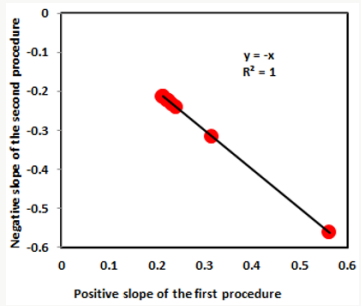
On the other hand, the Upper Shajara reservoir is separated from the Middle Shajara reservoir by yellow green mudstone as shown in Figure 1. It is defined by three samples so called SJ11, SJ12, SJ13 as explained in Table 1. Their positive slopes of the first procedure and negative slopes of the second procedure are displayed in Figures 9-11 and Table 1. Furthermore, their seismic time fractal dimension and capillary pressure fractal dimension are also higher than those of sample SJ3 and SJ4 from the Lower Shajara Reservoir owing to an increase in their permeability as explained in Table 1. Overall a plot of seismic time fractal dimension versus capillary pressure fractal dimension as shown in Figure 12 defines three permeable zones of varying petrophysical properties. These reservoir zones were also proofed by plotting slopes of the first procedure versus the slopes of the second procedure as shown in Figure 13. Such variation in fractal dimension can account for heterogeneity which is a key parameter in reservoir quality assessment.

Table 1: Petrophysical model showing the three Shajara Reservoir Units with their corresponding values of seismo electric transfer function fractal dimension and capillary pressure fractal dimension.

Conclusion

a) The sandstones of the Shajara Reservoirs of the permoCarboniferous Shajara formation were divided here into three units based on seismic time fractal dimension.

b) The Units from bottom to top are: Lower Shajara seismic time Fractal dimension Unit, Middle Shajara Seismic time Fractal Dimension Unit, and Upper Shajara Seismic time Fractal Dimension Unit.

c) These units were also proved by capillary pressure fractal dimension.

d) The fractal dimension was found to increase with increasing grain size and permeability.

Introduction

The author would like to thank King Saud University, college of Engineering, Department of Petroleum and Natural Gas Engineering, Department of Chemical Engineering, Research Centre at College of Engineering, and King Abdullah Institute for Research and Consulting Studies for their supports.

References

1. Toledo GT, Navy RA, Davis HT, Scriven LE (1994) Capillary pressure, water relative permeability, electrical conductivity and capillary dispersion coefficient of fractal porous media at low wetting phase saturation. SPE advanced technology Series 2: 136-141.
2. Li K, Horne RN (2002) Experimental verification of methods to calculate relative permeability using capillary pressure data. SPE 76757, Proceedings of the 2002 SPE Western Region Meeting/AAPG Pacific Section Joint Meeting held in Anchorage, Alaska
3. Li K, Willams W (2007) Determination of capillary Pressure function from resistivity data. Transp. Porous Media 67(1): 1-15.
4. Zhang Z, Weller A (2014) Fractal Dimension of Pore-Space Geometry of Eocene sandstone formation. Geophysics 79(6): D377-D387
5. Wang Z, Pan M, Shi Y, Liu L, Xiong F, et al. (2018) Fractal analysis of Donghetangs and stones using NMR measurements. Energy & Fuels 32(3): 2973-2982.
6. Guo Yu hang, Pan Bao zhi, Zhang Li hua, Fang Chuan hui (2018) Research and application of the relationship between transverse relaxation time and resistivity index in tight sandstone reservoir. Journal of petroleum Science and Engineering 160: 597-604.
7. AlKhidir KEME (2017) Pressure head fractal dimension for characterizing Shajara Reservoirs of the Shajara Formation of the Permo-Carboniferous Unayzah Group, Saudi Arabia. Archives of Petroleum and Environmental Biotechnology 1-7.
8. Alkhidir KEME (2018) Arithmetic relaxation time of induced polarization fractal dimension for characterizing Shajara Reservoirs of the Shajara Formation. Nanoscience and Nanotechnology 2(1):1-8
9. Alkhidir KEME (2018) Geometric relaxation time of induced polarization fractal dimensionfor characterizing Shajara Reservoirs of the Shajara formation of the Permo-Carboniferous Unayzah GroupPermo. International Journal of Petro chemical Research 2(1): 105-108.
10. Alkhidir KEME (2018) Geometric relaxation time of induced polarization fractal dimensionfor characterizing Shajara Reservoirs of The Shajara Formation of the Permo-Carboniferous Unayzah Group, Saudi Arabia. SiFed Journal of Petroleum 2(1): 1-6.
11. AlKhidir KEME (2018) Seismo Electric field fractal dimension for characterizing Shajara Reservoirs of the Permo-Carboniferous Shajara Formation, Saudi Arabia. Petroleum Petro Chemical Engineering Journal 2(4): 1-8.