Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2637-6652
Research Article(ISSN: 2637-6652) 
Hall Effects on MHD Convective Flow Through a Porous Medium Between Two Vertical Plates in Slip Flow Regime Volume 3 - Issue 2
VeeraKrishna M1*, Subba Reddy G1 and Ali J Chamkha2,3
- 1Department of Mathematics, Rayalaseema University, India
- 2Department of Mechanical Engineering, Prince Mohammad Bin Fahd University, Kingdom of Saudi Arabia
- 3RAK Research and Innovation Center, American University of Ras Al Khaimah, United Arab Emirates
Received: November 21, 2019 Published: December 11, 2019
Corresponding author: VeeraKrishna M, Department of Mathematics, Rayalaseema University, India
DOI: 10.32474/MAOPS.2019.03.000158
Abstract
In this paper, a probe on the impact of Hall effects on the flow of an oscillatory convective MHD viscous, incompressible, radiating and electrically conducting second-grade fluid in a vertical porous rotating channel in a slip flow regime is carried out. The fluid is assumed to be gray, absorbing and emitting radiation in a non-scattering medium. It is presupposed that MHD flow is laminar and fully developed. In order to use the regular perturbation technique, the solutions of velocity and temperature distributions for the governing flow are obtained. The profiles of velocity and temperature are presented graphically. On the other hand, the skin friction coefficient and the Nusselt number are evaluated numerically and presented in the form of tables, examined and discussed for various values of the flow parameters that govern it.
Keywords: Hall effect; radiating fluid; MHD oscillatory flow; rotating channel; slip flow regime
Introduction
Rapid efforts have been made to study the effects of various
fields in porous media by both experimentally and theoretically.
Flows through porous medium are of principal interest in the fields
of agricultural engineering, underground water resources and
seepage of water in riverbeds, filtration and purification processes
in ocean engineering, petroleum technology to study the movement
of natural gas, oil and water through the oil reservoirs. The way in
which fluid flow through porous media is of great importance for
the petroleum extraction processes. Most of the problems have
considerable practical significance besides contributing more to
the existing knowledge. Porous materials due to their inherent
capability are widely used in Ocean engineering, Mechanical
engineering, Medical appliances and Modern industrial fields.
The practical applications in geophysics and engineering promote
the study of flow in a rotating porous channel. Besides that, its
applications are extended to food processing industry, the chemical
processing industry, centrifugation filtration processes, and
rotating machinery. In addition to that, the hydrodynamic rotating
flow of electrically conducting viscous incompressible fluids has
garnered adequate consideration due to its variegated applications
in engineering and physics. In the domain of geophysics, it can be
applied to measure and study position and velocities with respect to
a fixed frame of reference on the surface of the earth, which rotates
with respect to an inertial frame in the presence of its magnetic field.
The area of geophysical dynamics, of late has become a significant
branch of fluid dynamics due to the enormous interest towards
environment and its concerns. As there is growing inquisitiveness
to study astrophysics, the research on fluid dynamics has become
vital as through it stellar and solar structures, interplanetary and
interstellar matter, solar storms, etc. can be studied. In engineering,
it finds its application in MHD generator ion propulsion, MHD
bearing, MHD pumps, MHD boundary layer control of re-entry
vehicles, etc. Several scholars [1-3] have studied such flows because
of their varied importance and applications.
The process of heat transfer is used in the cooling of nuclear
reactors, providing heat sink in turbine blades and aeronautics. There
are countless, significant engineering and geophysical applications
of channel flows through a porous medium: for example, in the field of agricultural engineering, for channel irrigation and for studying
underground water resources; and in petroleum technology, to
study the environment of natural gas, oil and water through the
oil channels/reservoirs. The transient natural convection between
two vertical walls with porous material having variable porosity
has been studied by [4]. In recent years, the effect of transversely
applied magnetic field on the flow of an electrically conducting
viscous fluid has been studied extensively owing to its astrophysics,
geophysical, and engineering applications. [5] have studied MHD
flow between the two parallel plates with heat transfer. When
the strength of magnetic field is strong, one cannot overlook or
negate the effect of Hall current. The rotating flow of an electrically
conducting fluid in the presence of a magnetic field is encountered
in geophysical and comical fluid dynamics. It is indispensable in
solar physics involved in sunspot development. The Hall effect on
unsteady MHD free and forced convection flow in a porous rotating
channel has been investigated by several researchers, including [6-
9]. Radiative convective flows have gained the attention of many
researchers in recent years. Radiation plays a crucial role in several
engineering, environment and industrial processes: for example,
heating and cooling chambers; fossil fuel combustion energy
processes; astrophysical flows; and space vehicle re-entry. [10]
studied radiation free convective flow through a porous medium
[11] have analysed the radiation effect on MHD flow through a
porous medium between infinite parallel plates in the presence
of time-dependent suction. [12] have studied the radiation effect
on the exact solution of free convective oscillatory flow through a
porous medium in a rotating porous channel.
The behaviour of the fluid under extreme confinement is of great interest from both the scientific and technological point of view. One of the great complexities and intricacies is to discover and unravel the type of boundary condition that is appropriate for solving the continuum fluid problems. Inspite of the widespread acceptance of the no-slip assumption, there has existed for many years indirect experimental evidence, based on anomalous flow in capillaries and other systems, that in some cases, a simple liquid can slip against the solid when walls are sufficiently smooth, and the no-slip boundary condition is no longer valid. The no-slip boundary condition holds good only when particles close to the surface fail to move along with the flow, i.e., when adhesion is stronger than cohesion. However, this is only true microscopically. Some other limitations of no-slip conditions are, they fail for large contact angles; they do not hold at very low pressure; they do not work for polyethylene, rubber compounds or suspensions; and they fail in hydrodynamics for hydrophobic surfaces [13]. Recently, the slip condition has become much more pronounced, and it is now reasonably sure that viscous fluid can slip against solid surfaces in the event of the surface being very smooth. The slip boundary condition has important application in lubrication, extrusion, and the medical sciences, especially in polishing article heart valves, flows through porous media, micro and nanofluids, friction studies and biological fluids [14]. On the other hand, chemical reactions have numerous applications, such as ceramic manufacturing, food processing, and polymer production. [15] has analyzed that the rate of diffusion is affected by chemical reaction. Many researchers have shown interest in propulsion engines for aircraft technology. Recently, [16] have analysed the effect of radiation on an unsteady MHD convective flow through a non-uniform horizontal channel. [17-21] investigated the Hall effect on an unsteady MHD oscillatory convective heat transfer flow of a radiating and chemically reacting fluid through a porous medium in a rotating vertical porous channel. Recently, [22] discussed the peristaltic MHD flow of an incompressible and electrically conducting Williamson fluid in a symmetric planar channel with heat and mass transfer under the effect of an inclined magnetic field. [23] discussed the theoretical and computational study of peristaltic hemodynamic flow of couple stress fluids through a porous medium under the influence of a magnetic field with wall slip condition. [24] discussed the MHD free convective rotating flow of visco-elastic fluid past an infinite vertical oscillating plate. [25] discussed the unsteady MHD convective flow of second grade fluid through a porous medium in a rotating parallel plate channel with a temperature-dependent source. [26] discussed heat and mass transfer on unsteady MHD oscillatory flow of blood through porous arteriole. In view of the above facts, in this paper, a probe or investigation is carried out of the influence of Hall effects on the flow of an oscillatory convective MHD viscous incompressible, radiating, and electrically conducting second grade fluid in a vertical porous rotating channel in slip flow regime.
Formulation and Solution of the Problem
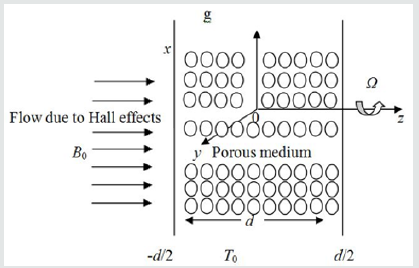
Consider the flow of a viscous, incompressible, and electrically conducting second grade fluid through a porous medium bounded by two infinite vertical insulated plates at d distance apart, under the influence of a uniform transverse magnetic field normal to the channel and taking Hall current into account. We introduce a Cartesian co-ordinate system with the x-axis oriented vertically upward along the centreline of this channel, and the z-axis taken perpendicular to the planes of the plates, which is the axis of the rotation, and the entire system comprising of the channel and the fluid are rotating as a solid body about this axis with constant angular velocity Ω. A constant injection velocity w0 is applied at the plate z = −d / 2 and the same constant suction velocity, w0 , is applied at the plate z = d / 2 . The schematic diagram of the physical problem is shown in Figure 1. Since the plates of the channel occupying the planes z = ± d / 2 are of infinite extent, all the physical quantities depend upon z and t only. Under the Boussinesq approximation, the flow of the fluid through a porous medium in a rotating channel is governed by the following equation:

When the strength of the magnetic field is very large, the generalized Ohm’s law is modified to include the Hall current, so that
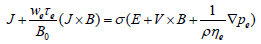 (2.7)
(2.7)In equation (2.5), the electron pressure gradient, the ion–slip effect, and the thermo-electric effect are neglected. We also assume that the electric field E=0 under assumption reduces to,

where m =τe ωe is the Hall parameter.
On solving the equations (2.8) and (2.9),
we obtain,

Using the equations (2.10) and (2.11), the equations (2.2) and (2.3) reduce:
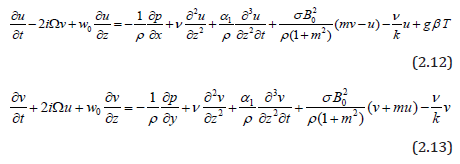
Following Cogley et al. [18], the last term in the energy equation stands for radiative heat flux, which is given by
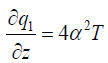 (2.14)
(2.14)whereα is the mean variation absorption coefficient.
Introducing non-dimensional variables,
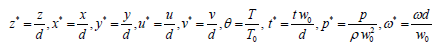
Making use of the non-dimensional variables, the equations (2.12), (2.13) and (2.4) reduce to (with the asterisks being dropped)
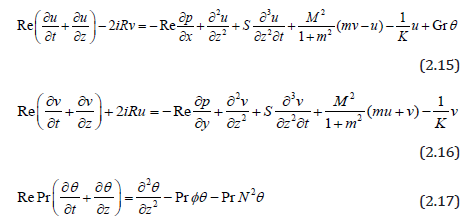
The corresponding boundary conditions in non-dimensional form are

We assume the flow under the influence of pressure gradient varying periodically with time,
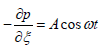 (2.21)
(2.21)Upon substitution of equation (2.21) into equation (2.20), we obtain
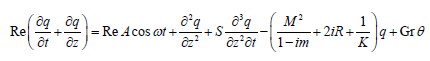 (2.22)
(2.22)The corresponding boundary conditions are
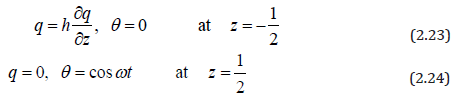
In order to solve the equations (2.22) & (2.17) with the boundary conditions (2.23) & (2.24), following Choudary et al. [19], we assume a solution of the form

Substituting the equations (2.25) and (2.26) in (2.22) and (2.17) respectively yields the following equations:
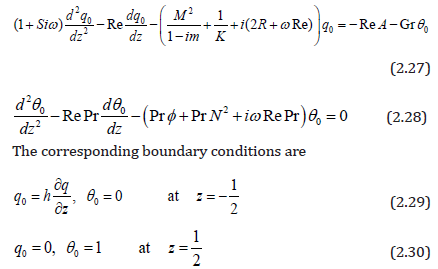
Solving the equations (2.27) and (2.28) with respect to the boundary conditions (2.29) and (2.30), we obtain the following expressions for the velocity and the temperature.
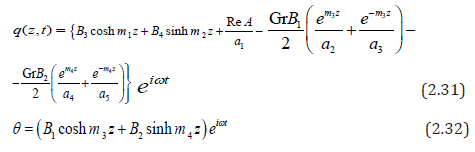
The validity and the correctness of the present solution are
verified by taking S = Gr = M = R= h = 0 and K →∞.
i.e., for the horizontal channel in the absence of rotation, slip flow and the condition of the ordinary medium so that
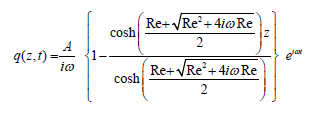 2 . 3 3 )
2 . 3 3 )This solution is reported by Schlichting and Gersten [20] for
periodic variation of the pressure gradient along axis of the channel.
We find the skin friction τL at the left plate in terms of its
amplitude and the phase angle as
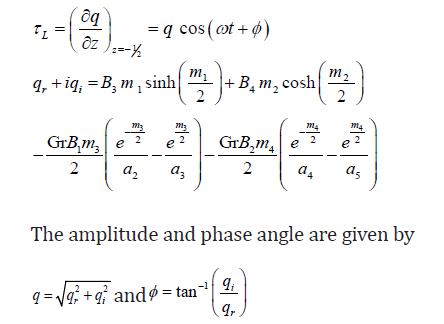
The rate of heat transfer (NU), in terms of amplitude and the phase angle, can be obtained as
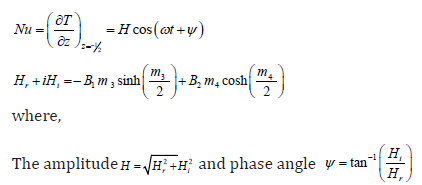
All the contents used above have been mentioned in the Appendix.
Results and Discussions
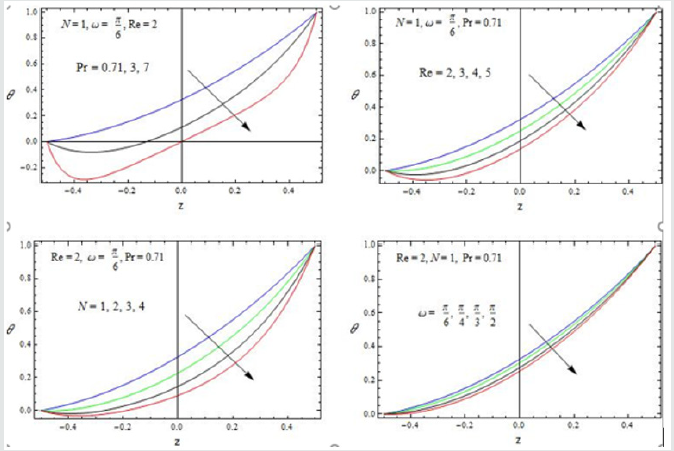
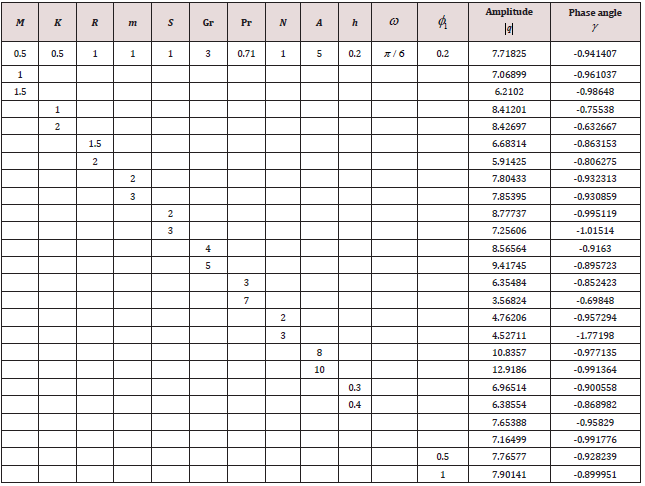
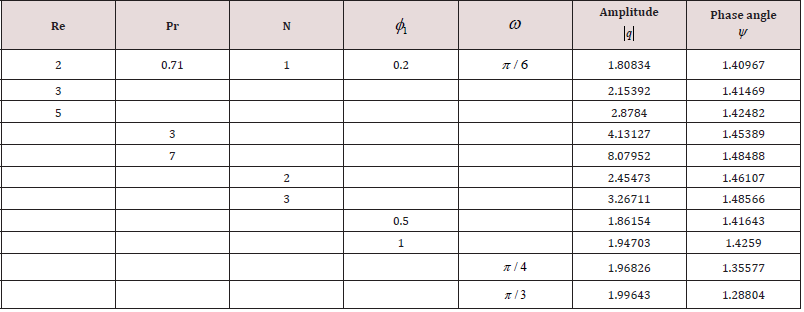
We have discussed the heat transfer on the flow of an oscillatory convective MHD viscous incompressible, radiating, and electrically conducting second grade fluid in a vertical porous rotating channel in slip flow regime, taking Hall current into account. The flow is governed by the non-dimensional parameters, namely, Re the Reynolds number, A the amplitude of pressure gradient, h the slip parameter, m the Hall parameter, R the rotation parameter, K the permeability parameter, Gr the thermal Grashof number, Pr the Prandtl number, N the Radiation parameter, φ1 the Heat absorption parameter, M the Hartmann number, S the second grade fluid parameter and ω the frequency of oscillation. The velocity profiles are depicted in Figures 2-5, while the temperature profiles are depicted in Figure 6. The skin friction and the Nusselt number are tabulated in Tables 1,2. For computational purposes, we are fixing the valuesRe = 2, t = 0.1 for the velocity profiles.
Figure 2:The velocity profiles for u and v against R, m and S with 1 Gr = 3,M = 0.5, Pr = 0.71, K = 0.5, A = 5, h = 0.2,φ1 = 0.1, N =1,ω =π
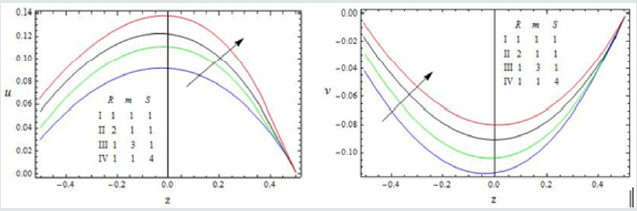
Figure 3: The velocity profiles for u and v against Gr, K and A with 1 R =1,M = 0.5, Pr = 0.71, m =1, S =1, h = 0.2,φ1 = 0.1, N =1,ω =π
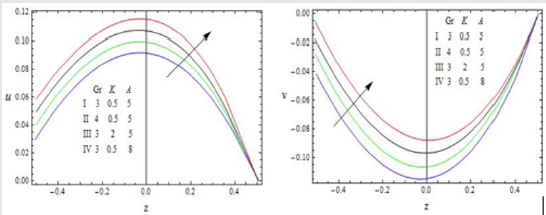
Figure 4: The velocity profiles for u and v against φ1 , h and ω with Gr = 3,M = 0.5, Pr = 0.71, K = 0.5, S =1,m =1, R =1, N =1, A = 5
Figure 5: The velocity profiles for u and v against M, Pr and N with 1 Gr = 3, S =1,m =1, R =1, K = 0.5, A = 5,h = 0.2,φ = 0.1,ω =π / 6
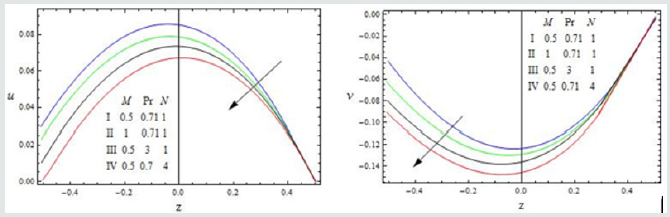
The effect of the rotation number R, the Hall parameter m, and the second-grade fluid parameter S on the velocity profile is shown in Figure 2. We notice that the magnitudes of velocity components u and v enhance with increasing values of R, m and S throughout the fluid region. A similar behaviour is observed for increasing thermal Grashof number Gr, permeability parameter K and the amplitude of the pressure gradient A Figure 3. It is observed from these Figures 4,5 that the velocity profile is diminished with the increase of all these parameters: the heat absorption parameter φ1 , the slip parameter h, the frequency of oscillationω , the Hartmann number M, the Prandtl number Pr, and the radiation parameter N. That is, it starts decreasing near the left plate of the channel. The variations in the temperature profile are presented in Figure 6. It is observed that the temperature profiles decrease with the increasing Reynolds number Re and the Prandtl number Pr. Likewise, the temperature profile is diminished with increasing the radiation parameter N and the frequency of oscillation ω .The skin friction and Nusselt number are evaluated analytically and tabulated in Tables 1,2. The amplitude and phase angle of the skin friction are shown in Table 1. The negative values in this table indicate that there is always a phase lag, and this phase goes on increasing with increasing frequency of oscillation. We notice that the amplitude |q| and phase angle γ of frictional force are enhanced with increasing the parameters S and A, and diminished with increasing h, Pr and R. The amplitude of the frictional force increases, and the phase angle of frictional force reduces with increasing the parameters K, Gr, m and φ1. The opposite behaviour is observed with increasing M, N and ω . Likewise, the amplitude of the Nusselt number and the magnitude of the phase angle increases with Re, Pr, N and φ1. The amplitude of the Nusselt number increases and the phase angle decreases with increasing ω .
Conclusions
The flow and heat transfer of an oscillatory convective MHD viscous incompressible, radiating and electrically conducting second grade fluid in a vertical porous rotating channel in slip flow regime and taking Hall current into account has been discussed.
1. The resultant velocity enhances with increasing R, m, Gr, K, A and S throughout the fluid region.
2. The velocity profile is diminished with the increase of φ1 , h, ω , M, Pr and N.
3. The temperature profiles decrease with the increasing Re, N, Prand ω .
4. The amplitude and phase angle of frictional force are enhanced with increasing S and A, and diminished with increasing h, Pr and R.
5. The amplitude of the frictional force increases, and the phase angle of frictional force reduces with increasing the parameters K, Gr, m and φ1
. The opposite behaviour is observed with increasing M, N and ω .
6. The amplitude of the Nusselt number and the magnitude of the phase angle increase with Re, Pr, N and φ1 . The amplitude of the Nusselt number increases and the phase angle decreases with increasing ω .
7. Nomenclature:
1(u, v): The velocity components along x and y directions
2P: The modified pressure
3t: Time
4: Specific heat
5B0: Electromagnetic induction
6g: Acceleration due to gravity
7K1: Thermal conductivity
8K: Permeability of the porous medium
9. Q0 : Heat absorption
10. T: Temperature of the fluid
11. f1 : Maxwell’s reflection co-efficient
12. μ : Co-efficient of viscosity
13. L : Mean free path
14. T0 : Mean temperature
15. w0 : Suction velocity
16. qsub>1 : Radiative heat
17. q: Complex velocity
18. M: Hartmann number
19. K: Permeability parameter
20. S: Second grade fluid parameter
21. E: Ekman number
22. Gr: Thermal Grashof number
23. Pr: Prandtl number
24. m: Hall parameter
7.1. Greek symbols
25. α : The mean variation absorption coefficient 26. α1: Normal stress moduli 27. θ : Dimension less temperature 28. Ù : Angular velocity 29. σ : Electrical conductivity of the fluid 30. ρ : Density of the fluid 31. ν : Kinematic viscosity 32. ω : The frequency of oscillation 33. β : The coefficient of volume expansion 34. ωe: The electron frequency 35. τe : The electron charge
7.2. Sub scripts
36. E: Electron
Appendix
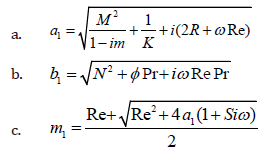

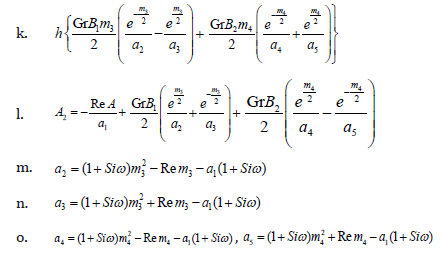
References
- Crammer KR, Pai SI (1973) Magneto fluid dynamics for engineers and applied physicists. McGraw-Hill Book Company New York.
- Ferraro VCA, Plumpton C (1966) An Introduction to Magneto Fluid Mechanics. Geophysical Journal International 12(5): 543-544.
- Shercliff JA (1965) A textbook of a magneto hydrodynamics. Journal of Fluid Mechanics 26(4): 840-843.
- Paul T, Singh AK, Misra Ak (2001) Transient natural convection between two vertical walls filled with a porous material having variable porosity. Mathematical Engineering in Industry 8(3).
- Attia HA, Kotb NA (1996) MHD Flow between Two Parallel Plates with Heat Transfer. Acta Mech 117(1-4): 215-220.
- Prasad Rao DRV, Krishna DV (1981) Hall effects on unsteady hydro magnetic flow. Indian J pure appl Math 12(2): 270-276.
- Singh KD, Kumar R (2009) Combined effects of Hall current and rotation on free convection MHD flow in a porous channel. IJPAP 47(9): 617-623.
- Singh KD, Pathak R (2012) Effect of rotation and Hall current on mixed convection MHD flow through porous medium filled in a vertical channel in presence of thermal radiation. Indian Journal of Pure and Applied Physics 50(2): 77-85.
- Ghosh SK, Beg OA, Narahari M (2009) Hall effects on MHD flow in a rotating system with heat transfer characteristics. Meccanica 44(6): 741-765.
- Raptis A (1998) Radiationand free convection flow through a porous medium. International Communications in Heat and Mass Transfer 25(2): 289-295.
- Agolia KD, Tay G, Abbey TM (1998) Radiative and free convective effects of a MHD flow through a porous medium between infinite parallel plates with time-dependent suction. Astrophysics and Space Science 260: 455-468.
- Singh KD, Kumar R (2009) Radiation effects on the exact solution of free convective oscillatory flow through porous medium in a rotating vertical channel. Journal of Rajasthan Academy of physical sciences 8(3): 295-310.
- Vinogrodova (1995) Drainage of a thin liquid-film confined between hydrophobic surfaces. Langmuir 11(6): 2213-2220.
- Blake TD (1990) Slip between a liquid and a solid: D.M. Tolstoi's (1952) theory reconsidered. Colloids and Surfaces 47: 135-145.
- Muthucumaraswamy R (2010) Chemical reaction effects on vertical oscillating plate with variable temperature. Chemical industry and Chemical Engineering Quarterly 16(2): 167-173.
- Reddy KJ, Sunitha K, Reddy MJ (2012) The radiation effect on the unsteady MHD convection flow through a nonuniform horizontal channel. Advances in Applied science and Research 3(3): 1231-1238.
- Street RE (1960) A study of a boundary condition in slip flow. Aerodynamics of rarefied Gas dynamics (FM Devienne, ed) Dergamen.
- Cogley AC, Vincenti WG, Gilles SE (1968) Differential approximation for radiative transfer in a Non-grey gas near equilibrium. AIAA Journal 6: 551-553.
- Chaudhary RC, Jha, AK, Dhayal SS (2006) Heat transfer to Magneto- hydrodynamic flow in a horizontal channel with heat source. Journal of Rajasthan Academy of physical sciences 5(2): 233-
- Schlichting H, Gersten K (2001) Boundary layer theory, (8th Edition); Springer.
- K Chand, KD Singh and S Kumar (2012) Hall effect on radiating and chemically reacting MHD oscillatory flow in a rotating porous vertical channel in slip flow regime. Advances in Applied Science Research 3(4): 2424-2437.
- Veera Krishna M, BV Swarnalathamma (2016) “Convective Heat and Mass Transfer on MHD Peristaltic Flow of Williamson Fluid with the Effect of Inclined Magnetic Field.” AIP Conference Proceedings 1728:
- Swarnalathamma B V, M Veera Krishna (2016) Peristaltic hemodynamic flow of couple stress fluid through a porous medium under the influence of magnetic field with slip effect. AIP Conference Proceedings 1728:
- VeeraKrishna M, M Gangadhar Reddy (2016) MHD free convective rotating flow of Visco-elastic fluid past an infinite vertical oscillating porous plate with chemical reaction IOP Conf. Series: Materials Science and Engineering 149:
- VeeraKrishna M, G Subba Reddy (2016) Unsteady MHD convective flow of Second grade fluid through a porous medium in a Rotating parallel plate channel with temperature dependent source IOP Conf. Series: Materials Science and Engineering 149:
- Veera Krishna M, BV Swarnalathamma, J Prakash (2018) “Heat and mass transfer on unsteady MHD Oscillatory flow of blood through porous arteriole. Applications of Fluid Dynamics Pp: 207-224.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...