Constructing a Three-Dimensional Histogram Describing Dislocation Viscous Glide and Climb Mechanisms Volume 3 - Issue 2

Furong Cao¹* and Xiaotong Zhu^1,2

• ¹School of Materials Science and Engineering, Northeastern University, PR China
• ²Huaian Dekema Semiconductor Co, Ltd., Huaian 223300, PR China

Received: August 11, 2020;   Published: September 08, 2020

*Corresponding author: Furong Cao, School of Materials Science and Engineering, Northeastern University, Shenyang 110819, PR China

DOI: 10.32474/MAMS.2020.03.000160

Abstract PDF

Abstract

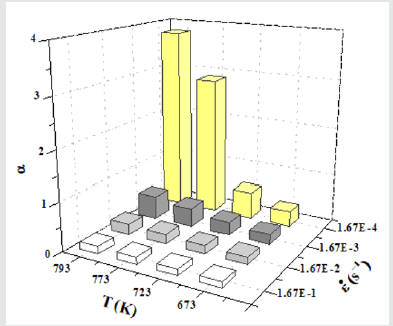
Dislocation creep is one of creep mechanisms. Elucidating creep mechanism is beneficial to understand the nature of hightemperature creep deformation and control the slow deformation of service devices at elevated temperatures and their accuracies of dimensions. In this paper, a factor α, was proposed to determine quantitatively the mechanisms of dislocation viscous glide (solute drag creep) and climb. When α>1, dislocation viscous glide or solute drag creep dominates while when α<1, dislocation climb dominates. A calculated example was given, and a three-dimensional histogram was constructed in Al-1.44Mg-1.09Y alloy tensile at elevated temperatures. The results revealed that at 773 and 793 K and at an initial strain rate of 1.67×10-4 s-1, the ratecontrolling mechanism is dislocation viscous glide or solute drag creep, whereas under other conditions, the rate-controlling mechanism is dislocation climb.

Summary

Bit-wrong creep is one of the mechanisms of creep. It is of great significance to reveal the material creep mechanism for understanding the essence of high temperature deformation of material and the precision of slow deformation control of high temperature service devices. In this paper, a judge factor of determining the misalignment of the bit viscous slip (solute drag creep) and the climbing mechanism is alpha. The misalignment of the sliding mechanism is the dominant mechanism when alpha is 1, and when alpha-lt;1, the misalignment mechanism is the dominant mechanism. An example of calculation is given and a threedimensional hele chart is constructed in the Al-1.44Mg-1.09Y alloy stretched at high temperature. The results show that under the conditions of temperature of 773K and 793K and strain rate of 1.67 x 10-4 s-1, Under conditions, the speed control mechanism is mispositioned viscosity slip or solute drag creep, and under other conditions, the speed control mechanism is the faulty climbing mechanism [1-4].

Keywords: Creep, dislocation viscous glide; dislocation climb; judging factor, three-dimensional histogram; misalignment of viscous slip; determining factors

Introduction

Creep is the process by which material occurs at high temperatures and its slow deformation process. -2 since the slow deformation of high temperature service devices under thermal coupling cooperation directly affects the accuracy -4 of instrument size, so the study of creep and its mechanism has attracted attention [to the situation. Creep mechanisms include diffusion creep, misplaced creep, and superplastic creep. Misplaced creep includes misalignment of staggered slips (solute drag creep) and misplaced climbs. Over the years, Western scholars have proposed and studied the creep mechanism, and-10] 5 [9 the. 8] constructed the. a two-dimensional deformation mechanism diagram in a singlephase and quasi-single-phase alloy, as well as a two-dimensional. deformation mechanism diagram in a two-phase alloy. Deformation mechanism diagram is a useful tool for describing deformation mechanism, the development process is detailed in the literature 1. Its scientific value lies in the quantitative rather than qualitative description of the mechanism of material creep. This is of great significance for revealing the nature of creep process in depth. The problem is that creep model parameters are more difficult to obtain and lack a more intuitive expression, thus limiting their application. The literature analysis shows that there are no three-dimensional barricades and practical computational examples in the theory of bit-wrong creep. Therefore, this paper presents a determination factor for bit misalignment sliding (solute drag creep) and bit-wrong climbing mechanism, giving calculation examples and constructing an intuitive three-dimensional heliograph. It is hoped that it will provide useful help to deepen the intuitive understanding of creep mechanism [5-9].

Model

The solid solute under the action of high temperature external force, the crystal mid-position mission slip (solute drag creep) and the bit mis-climbing, resulting in slip resistance and climbing resistance. The resistance coefficient is used in the literature. The coefficient of resistance for mispositioned viscosity slip (solute drag creep) is 12-13.

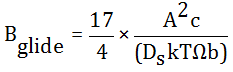(1)

Where A=(3GbΩe)/πk is the Boltzmann constant, T is the deformation temperature, e is the difference ratio of the solute and solvent atomic fraction dimensions, c is the atomic percentage of the solute, b is the Cypress vector, the o is the atomic volume, G is the shear die, and Ds is the diffusion coefficient of the solute atom.
The coefficient of resistance for the mis-climbing of the bit is 13-15

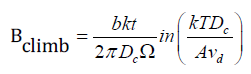(2)

Where Dc is the diffusion coefficient for misalignment and vd is the misplaced movement speed, wherein it isv_d=ε ̇/(ρb) the strain rate, and ε ̇the di location density.

We order.

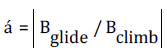(3)

The mechanism of misalignment of viscosity (solute drag creep) is the dominant mechanism when alpha is 1, and when alpha-lt;1, the misalignment mechanism is the dominant mechanism. According to [13 Soer et al], due to the sequential process of misalignment and climbing, large drag coefficients determine the speed control mechanism. Therefore, the solute and the misalignment of the solute have a strong effect on the formation of the Koch gas group, indicating the existence of solute drag creep, therefore, the speed control mechanism is bit-wrong viscosity slip or solute drag creep, stress index n3. Alpha-lt;1, the reforest, the solute and the misalignment of the ability to form the Koch gas group weakened in a secondary position, the misalignment of the position occupies the dominant position, therefore, the speed control mechanism is the misalignment mechanism, stress index ns 5.

Calculate Instances and Three-Dimensional Histograms

Study 6. Study 6. Study al-1.44Mg-1.09Y gold temperature for the gold-based monophasic gold its Mg is solute, Al is solvent, Y for the form of the two-phase added in order to pick -model (1) - (3) calculation data, first obtained the model: k-1.38-10^-23J/K, T-793 K, e'12.08%'0.1208 ,17,c and model' '1.8%'0.018 s.18'; b is the Cypress vector. For aluminum (in), b'2.86^-10 m '19', '1.66'10^-29m³ ,19 s) Ds for solute Mg diffusion coefficient, Ds'1.24-10^-4exp (-130500/RT) m²/s," R is the gas constant .8.314J/molK ;Dc is the wrong climbing diffusion coefficient, Dc'1.86'10^-4exp (143400/RT) m²/s (20c) '1.67^-10, .4s^-1' '1010 m^-2' shear module, For G, E^-2, 1, 1, 1, Pobie, on aluminum -0.34 s.19. For example, the deformation temperature of 793 K and the strain rate of 1.67 x 10^-4s^-1 conditions are calculated. The T-793K and s.34 were brought into the Model G,"""Ukal." The resulting G-value and the above data are brought in, and you get A.96 x 10A? (3Gb? e)/-30. The spread coefficient model was replaced with the T-793K model, and the Ds were obtained, with Ds. 3.14 x 10^-13m²/s and Dc-6.66 x 10^-14m²/s. Bring the misalignment density equivalent into the misplaced movement speed vd model, 5.84 x 10, v-d^-5m/s. The models A, c, k, T, Ds, O and B are replaced with models (1), and Bglide is obtained by Bglide. The parameters A, b, k, T, Dc, O, and vd are replaced into the model (2), and the Bclimb is 1.17 x 1011. Thus, according to the model (3) to obtain the alpha 3.8 1. Therefore, the deformation mechanism under the condition of strain rate of 1.67 x 10^-4s^-1 is mispositioned viscose slip (solute drag creep)[10-16].

By this, you get the alpha factor value under other conditions, and then construct a T-alpha three-dimensional ε ̇bar chart, as shown in(Figure 1).It can be seen from the three-dimensional heliogram that at temperatures of 773 K and 793 K, with strain rates of 1.67 x 10 α<1，The speed control mechanism is the fault-climbing mechanism, and the stress index is n-5-4 s^-1, under the condition.，2 data alpha-gt;1, speed control mechanisms are misplaced viscosity slip or solute drag creep, stress index nns 3;Under other conditions, 14 data. The results of the bar chart determined by the mechanical data are [16]very consistent with the prediction of the deformation mechanism diagram in the literature.The introduction of alpha determination factors and three-dimensional histograms makes the determination of the fault creep mechanism simple and straightforward, and it is expected to help to deepen the understanding of the nature of creep.

Conclusion

A criterion factor for determining the bit error viscosity slip (solute drag creep) and the climbing mechanism is proposed. The misalignment of the sliding mechanism is the dominant mechanism when alpha is 1, and when alpha-lt;1, the misalignment mechanism is the dominant mechanism. An example of calculation is given, and a three-dimensional hetle chart is constructed in the Al-1.44Mg- 1.09Y alloy stretched at high temperature. The results show that under the conditions of temperature of 773 K and 793 K and strain rate of 1.67 x 10-4 The mechanism is misplaced climbing speed control s-1, under the condition, the speed control mechanism is mispositioned viscosity slip or solute drag creep; Under other conditions, the misalignment [17-20].

Fund Projects

National Natural Science Foundation of China (No.51334006).

References

1. Kassner ME (2009) Fundamental of Creep in Metals and Alloys. Elsevier, Oxford, UK.
2. Kassner ME, Peres-Prado MT (2000) Five-Power-Law Creep in Single Phase Metals and Alloys. Progress in Materials Science 45: 1-102.
3. Langdon TG (2005) An Analysis of Flow Mechanism in High Temperature Creep and Superplasticity. Materials Transactions 46:1951-1956.
4. Spigarelli S, Paoletti C (2018) A New Model for the Description of Creep Behaviour of Aluminum-Based Composites Reinforced with Nanosized Particles. Composites Part A 112: 346-355.
5. Ashby MF (1972) A First Report on Deformation-Mechanism Maps. Acta Metallurgica 20: 887-897.
6. Mohamed FA, Langdon TG (1976) Deformation Mechanism Maps for Solid Solution Alloys. ScriptaMetallurgica 9: 137-140.
7. Langdon TG, Mohamed FA (1978) A New Type of Deformation Mechanism Map for High-temperature Creep. Materials Science and Engineering 32: 103-112.
8. Ruano OA, Wadsworth J, Sherby OD (1985) Deformation Mechanisms in an Austenitic Stainless Steel (25Cr-20Ni) at Elvated Temperature. Journal of Materials Science 20: 3735-3744.
9. Kawasaki M, Langdon TG (2012) Using Deformation Mechanism Map to Depict Flow Processes in Superplastic Ultrafine-grained Materials. Journal of Materials Science 47: 7726-7734.
10. Mohamed FA (2011) Deformation Mechanism Map for Micro-grained, Ultrafine-grained, and Nano-grained Materials. Materials Science and Engineering A 528: 1431-1435.
11. Cao Furong (2014) Metal Superplasticity. Metallurgical Industry Press, Beijing.
12. Cottrell AH, Jaswon MA (1949) Distribution of solute atoms round a slow dislocation. Proceedings of The Royal Society A 199: 104-114.
13. Soer WA, Chezan AR, HossonJThMDe (2006) Deformation and reconstruction mechanisms in coarse-grained superplastic Al-Mg alloys. Acta Materialia 54: 3827-3833.
14. Hirth JP, Lothe J (1968) Theory of dislocations. John Wiley, New York, NY, USA.
15. Takeuchi A., Argon AS (1976) Steady-state creep of alloys due to viscous motion of dislocations. Acta Metallurgica 24: 883-889.
16. Cao Furong, Zhu Xiaotong, Wang Shuncheng, Shi Lu, Xu Guangming, et al. (2017) Quasi-superplasticity of a Banded-Grained Al-Mg-Y alloy Processed by Continuous Casting-Extrusion. Materials Science and Engineering A 690: 433-445.
17. King HW (1966) Quantitative Size-Factors for Metallic Solid Solutions. Journal of Materials Science 1: 79-90.
18. Massalski TB, Okamoto H, Subramanian PR (2011) Binary Alloy Phase Diagrams, Second edition plus updates. ASM International OH.
19. Frost HJ, Ashby MF (1982) Deformation Mechanism Maps, Pergamon Press, Oxford, UK p.21.
20. Yavari P, Langdon TG (1982) An Examination of the Breakdown in Creep by Viscous Glide in Solid Solution Alloys at High Stress Levels. Acta Metallurgica 30: 2181-2196.