Random Graph Models with Non-Independent Edges

Volume 2 - Issue 1

Zohre Ranjbar Mojaveri and Andras Farago*

Received: November 24, 2020;   Published: November 30, 2020

DOI: 10.32474/CTCSA.2020.02.000130

Full Text PDF

To view the Full Article   Peer-reviewed Article PDF

Abstract

Random graph models play an important role in describing networks with random structural features. The most classical model with the largest number of existing results is the Erd˝os-R´enyi random graph, in which the edges are chosen interdependently at random, with the same probability. In many real-life situations, however, the independence assumption is not realistic. We consider random graphs in which the edges are allowed to be dependent. In our model the edge dependence is quite general, we call it p-robust random graph. Our main result is that for any monotone graph property, the p-robust random graph has at least as high probability to have the property as an Erd˝os-R´enyi random graph with edge probability p. This is very useful, as it allows the adaptation of many results from Erd˝os-R´enyi random graphs to a non-independent setting, as lower bounds.
Random networks occur in many practical scenarios. Some examples are wireless ad-hoc networks, various social networks, the web graph describing the World Wide Web, and a multitude of others. Random graph models are often used to describe and analyze such networks. The oldest and most researched random graph model is the Erd˝os-R´enyi random graph G_{n, p}. This denotes a random graph on n nodes, such that each edge is added with probability p, and it is done independently for each edge. A large number of deep results are available about such random graphs, see expositions in the books [1-4]. Below we list some examples. They are asymptotic results, and for simplicity we ignore rounding issues (i.e., an asymptotic formula may provide a non-integer value for a parameter which is defined as integer for finite graphs).

The size of a maximum clique in G_{n, p} is asymptotically 2log_1/p n .

If G_{n, p} has average degree d, then its maximum independent set has asymptotic size (2n In d) / d .

The chromatic number of n, p G is asymptotically n/log_bn, where b=1-p

The size of a minimum dominating set in G_{n, p} is asymptotically n/log_bn, where b=1/1-p

The length of the longest cycle in G_{n, p}, when the graph has a constant average degree d, is asymptotically n(1− de^−d ) .

The diameter of G_{n, p} is asymptotically log n/ log(np), when np → ∞ . (If the graph is not connected, then the diameter is defined as the largest diameter of its connected components.)

If G_{n, p} has average degree d, then the number of nodes of degree k in the graph is asymptotically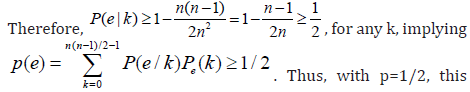

However, the requirement that the edges are independent is often a severe restriction in modelling real-life networks. Therefore, numerous attempts have been made to develop models with various dependencies among the edges, see a survey in [2]. Here we consider a general form of edge dependency. We call a random graph with this type of dependency a p-robust random graph.

Abstract| Definition 1 (p-robust random graph)| Definition 2 (Monotone Graph Property)| References|