Applying Biologically Inspired Optimization Approaches to Osmotic Dehydration Volume 7 - Issue 5

Julian Scott Yeomans*

• Schulich School of Business, York University, Canada

Received: November 16, 2019;   Published: November 22, 2019

Corresponding author: Julian Scott Yeomans, OMIS Area, Schulich School of Business, York University, Toronto, Canada

DOI: 10.32474/CIACR.2019.07.000275

Abstract PDF

Abstract

In osmotic dehydration application, the functional form of the dehydration model can be established through a response surface technique and the resulting mathematical formulation can be transformed into a non-linear goal programming model. A biologically inspired optimization algorithm for finding the best processing parameters should be considered, since the results can be shown superior to previous approaches.

Introduction

The high moisture content in many fresh fruits and vegetables renders them extremely perishable, since deterioration commences immediately upon harvesting Venturini et al. [1]. Preservation of many agricultural commodities can be accomplished by various drying combinations of heat processing and dehydration Ranganna [2]. Hot-air dried products have not received widespread acceptance due to the perceived diminished quality of the end product Venturini et al. [1]. Osmotic dehydration has been introduced as an alternative that can produce higher quality final products Rastogi et al. [3]. In osmotic dehydration, fresh produce is immersed in a hypertonic solution where the water content from the cells of the produce is transferred into the solution due to the relative differences in their solute concentrations Rastogi et al. [3]. Simultaneously, a corresponding transfer of solid materials (normally sugar and/or salt) occurs from the solution into the product Tonon et al. [4]; Nieto et al. [5]; Rastogi et al. [3]. Relative to standard hot air drying methods, osmotic dehydration causes minimal thermal degradation due to the low temperatures involved Jain et al. [6]; Rastogi et al. [3]. The quality of the subsequent product is superior due to

a. The improvements to texture of the fruits and vegetables,

b. The stability of the color pigmentation during storage, and

c. Increases in the solid gain transfer of sugar and salt from the hypertonic solution Jain et al. [6]; Venturini et al. [1].

Water removal during the dehydration process is influenced by many factors such as type and concentration of osmotic agents, temperature, circulation/agitation of solution, solution-to-sample ratio, thickness of food material, and any pre-treatments Rastogi et al. [3]. An effective analysis of the mass transport occurring within the osmosis process measured in terms of water loss and solid (sugar, salt) gains is of considerable commercial and practical relevance Nieto et al. [5]; Rastogi et al. [3]. Only limited attention has been devoted to optimizing the requisite osmotic process parameters Cao & Yeomans [7]. Biologically inspired algorithms provide optimization approaches based on (mostly successful) mechanisms in the natural world Yang [8]; Yeomans & Yang [9]. The benefits of biologically inspired, osmotic dehydration optimization can be illustrated via the papaya case of Jain et al. [6].

Functional Form Estimation and Optimization of the Osmotic Dehydration Process

In the papaya case, a syrup solution is employed for dehydration and the solid gain corresponds to the transport of sugar from the syrup into the papayas. The initial step requires the construction of a mathematical model of the responses to the three main osmotic process parameters –
a. Solution temperature,
b. Hypertonic solution concentration and
c. Duration of osmosis – on the water loss and solid gain of the papayas.
This functional representation is then used to predict the water loss and sugar gain impacts in the papayas over the requisite experimental ranges of three designated process parameters. In osmotic processes, the exact relationship between the dehydration parameters is generally not known a priori. Hence, the functional form of the osmotic dehydration process can be approximated empirically using response surface techniques Mudhar et al. [10]; Myers & Montgomery [11]; Yeomans & Yang [9]. The response model can then be used to determine the maximum water loss and optimum sugar gain achieved during the dehydration of papayas over the different experimental ranges for the process durations, syrup concentrations, and solution temperatures.
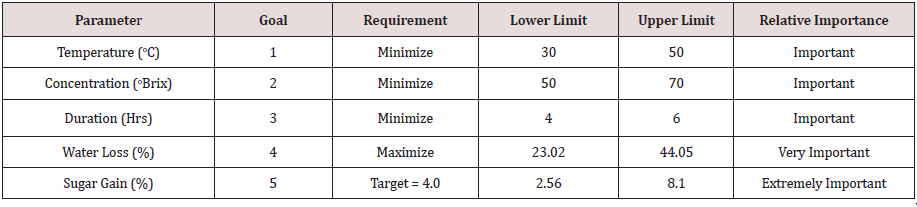
Organoleptic properties refer to the sensory aspects of food including taste, sight, smell, touch, dryness, moisture content, and stale-fresh factors. Jain et al. [6] established organoleptic ranges for the osmotic dehydration parameters and restricted the search for best parameter settings to values within these ranges. Additional organoleptic preferences can be applied to the responses and process parameters for the solution. The targets for these desired criteria are summarized in Table 1. From a hierarchical preference attainment perspective, several of these criteria can be recognized as more important attributes to satisfy than the others. Namely, from a dehydration perspective, the water loss should be as high as possible within the indicated range, while from a taste perspective, the sugar gain needs to be as close to 4.0% as possible. The relative importance for the achievement of these hierarchy targets is indicated in the last column of Table 1.

In order to find values for the osmotic dehydration parameters, Jain et al. [6] ,constructed a number of contour plots by varying the values of the three variables and observed the effect that these had on their response functions. These settings invoke responses of 28% for the water loss and 4.0% for the sugar gain see Table 2. Conversely, from a mathematical perspective, each of the desired targets could be specified as a definitive goal and the entire formulation could then be transformed into a non-linear goal programming problem Yeomans & Yang [9]. The biologically inspired, Firefly Algorithm (FA) Yang [8] is then used to find the optimal osmotic parameters for the papaya dehydration. By optimizing the goal programming problem formulation using the FA-driven procedure, best process parameters for the osmotic dehydration of the papayas were calculated and these resulting values are displayed in Table 2. In comparison to the values found by Jain et al. [6], it can be observed the temperature parameter remains essentially the same, the syrup concentration increases by 10 oBrix, while the duration of dehydration process has been reduced slightly by 0.25 hours. More importantly, in terms of the key responses, while the sugar gain essentially remains at the highly desirable target of 4%, the water loss–which is obviously the key feature of dehydration–has increased by 5%. Consequently, since the water loss response has been increased significantly from that determined by Jain et al. [6], this goal programming solution represents a significant improvement in the osmotic dehydration process.

Conclusion

An empirical response surface approach can provide the functional form required for osmotic dehydration. Using these values, the resulting optimization model can be formulated into a non-linear goal programming problem. The optimal solution to the goal programming formulation can be solved using a computationally efficient, biologically inspired procedure and the resulting best osmotic parameters can be ascertained. Since biologically inspired optimization algorithms can clearly be adapted to solve a wide spectrum of osmotic dehydration problems beyond the context of papaya, the described approach can obviously be extended into numerous other applications.

References

1. Venturini ME, Reyes JE, Rivera CS, Oria R, Blanco D (2011) Microbiological Quality and Safety of Fresh Cultivated and Wild Mushrooms Commercialized in Spain. Food Microbiology 28(8): 1492-1498.
2. Ranganna S (1986) Handbook of analysis and quality control for fruits and vegetable products. Tata McGraw Hill Publishing. New Delhi, India.
3. Rastogi NK, Raghavarao KSMS, Niranjan K, Knorr D (2002) Recent developments in osmotic dehydration: Method to enhance mass transfer. Food Science Technology 13(2):48-59.
4. Tonon RV, Baroni AF, Hubinges MD (2007) Osmotic Dehydration of Tomato in Ternary Solutions: Influence of Process Variables on Mass Transfer Kinetics and an Evaluation of the Retention of Arytenoids. Food Engineering 82(4): 509-517.
5. Nieto A, Castro MA, Alzamora A (2001) Kinetics of moisture transfer during air drying of blanched and/or osmotically dehydrated mango. Journal of Food Engineering 50(3): 175-185.
6. Jain SK, Verma RC, Murdia LK, Jain HK, Sharma GP (2011) Optimization of Process Parameters for Osmotic Dehydration of Papaya Cubes. Food Science and Technology 48(2): 211-217.
7. Cao T, and Yeomans JS (2016) The Calculation of Optimal Osmotic Dehydration Process Parameters for Mushrooms: A Firefly Algorithm. International Journal of Environmental and Agriculture Research 2(12): 52-58.
8. Yang XS (2010) Nature-Inspired Metaheuristic Algorithms (2^nd);Luniver Press. Frome, UK.
9. Yang JS, Yang XS (2014) Determining Optimal Osmotic Drying Parameters Using the Firefly Algorithm. 6^th International Conference on Applied Operational Research (ICAOR). 6: 32-39.
10. Mudhar GS, Toledo RT, Floros JD, Jen JJ (1989) Optimization of carrot dehydration process using response surface methodology. Journal of Food Science 54(3): 714-719.
11. Myers RH, Montgomery DC (1995) Response Surface Methodology: Process and Product Optimization Using Designed Experiments. John Wiley and Sons, New York, USA.