
Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6736
Review Article(ISSN: 2643-6736) 
Development of Novel Composite Biomaterials for Use as Biodegradable Adsorbents and or Bio-Carriers During Wastewater Treatments Using Galerkin’s Finite Element Analysis Volume 3 - Issue 2
Nwaiwu Uchechukwu1*, Nwasuka Cyprian Nnamdi1, Nwogu Chukwunonso Nweze2, Nwadinobi Chibundo Princewill1 and Nnamani Afamefuna Pascal3
- 1Department of Mechanical Engineering, Abia State University, Nigeria
- 2Department of Mechanical Engineering, Michael Okpara University of Agriculture Umudike, Umudike
- 3Department of Autotronics Engineering, Skill ‘G’ Nigeria Limited, Abuja
Received:July 16, 2021 Published: August 24, 2021
Corresponding author: Nwaiwu Uchechukwu, Department of Mechanical Engineering, Abia State University, PMB 2000, Uturu, Nigeria
DOI: 10.32474/ARME.2021.03.000156
Abstract
In this study, the development of novel composite biomaterials for use as biodegradable adsorbents and or bio-carriers during wastewater treatments was carried out using Galerkin’s finite element analysis. Several literatures in the past showed that the increment in number of wastewater treatment plants, made it difficult to manage the wastewater systems. Therefore, to ensure proper discharge from the wastewater treatment plants, new and stricter regulations for nutrient removal have to be incorporated. Several wastewater treatment measures that have been adapted to date includes: bio filtration, ion exchange, sedimentation, solvent extraction, chemical oxidation, membrane processes, coagulation, oxidation, Fenton process, and electro coagulation. The data used in this analysis were obtained from various literature sources and were analyzed using Galerkin’s finite element analysis method in order to develop models that would analyze the empirical parameters affecting wastewater treatments. The result obtained showed that the removal efficiencies for wet season are TDS (16), BOD (63), COD (55.8) and N (72%) respectively. The results justified the presence of high impurities as a result of influx of wastes from industries, households etc into the river body.
Introduction
Freshwater is the chief constituent of the planet and is essential for the survival of all living organisms [1-5]. The continuous addition of undesirable chemicals, agricultural wastes [11], civilization, industrial wastes, other environmental and global changes etc. reduced the quality of water resources [18]. Over the last century, major part of the world has been facing degradation of environment because of the continuous growth in population [12]. With the growing population, there is a striking increase in usage and wastage of water for domestic purposes. Domestic wastewater is usually the water discharged from household purposes such as toilets, dishwashers, showers, sinks, washing machines etc. [8]. The contamination due to organic pollutants is very dangerous due to their various side effects and carcinogenic nature. Several literatures reveal some methods for the removal of organic pollutants from water. The methods used in literature suggested that the methods might depend on their physical, chemical, electrical, thermal and biological properties [13-17].
While other researchers proposed that oxidation, reverse osmosis, ion exchange, electro-dialysis, electrolysis, adsorption as another method of wastewater removal etc. Of course, reverse osmosis, ion exchange, electro-dialysis, electrolysis and adsorption are excellent wastewater removal technologies. Several reviews were made in the past in order to determine the best wastewater removal technique. Others argued that before talking about wastewater removal technique, that it is imperative to firstly divide the wastewater treatment procedures into primary and secondary treatment processes depending on either the removal of solid particles physically by using screens or biological treatment where microorganisms consume organic matter and convert it into inorganic compounds. [6-7] Nitrogen and phosphorus removal are the major goals of wastewater treatment which can be carried out biologically in an economically feasible and environmentally friendly manner in recent years [19]. In case of phosphorus, sometimes biological methods are not efficient because of lack of carbon. Hence, to make up for the lack of carbon, some additional organic matter is added to the biological reactors which increases the cost of operation and results in generation of one more pollutant. However, there is an alternative for this problem which is the use of enhanced biological phosphorus removal which works efficiently for domestic waters with Low C/N ratio [1]. Nowadays, with the increment in number of wastewater treatment plants, it has become challenging to manage the wastewater systems. Therefore, to ensure proper discharge from the wastewater treatment plants, new and stricter regulations for nutrient removal have been incorporated. Several wastewater treatment measures that have been adapted to date include bio filtration, ion exchange, sedimentation, solvent extraction, chemical oxidation, membrane processes, coagulation, oxidation, Fenton process, and electro coagulation [1,2].
Adsorption is today regarded as the best water treatment procedure because of its universal nature, ease of operation and inexpensiveness.it has a removal capacity rate of 99.9% .The adsorption has some limits which made its removal rates not to perfect [9-20]. To comply with these limits, there is a need for modeling and operation control of wastewater treatment plants. However, the modeling of wastewater treatment systems tends to become intricate due to certain characteristics such as unusually long residence times, plenty of tunable kinetic parameters and large variations in influent component flow rates. Nevertheless, with the advancements in technology, activated sludge modeling, flow sheet simulators and computational fluid dynamics have emerged as some significant tools for modeling Wastewater treatment plants. Over the years, dynamic modeling has come across as a remarkable approach for developing operational models in process design and management. Moreover, these Models help in establishing operating policies and control strategies for the wastewater treatment plants which in turn maximizes the plant performance and comply with the required permit limits. The mathematical modeling of wastewater, the performance of the pH, dissolved oxygen demands, and other wastewater analytical parameters were not captured in literature
Mathematical Formulation:
The mathematical formulation can be carried out by considering the following assumptions
1. The evolution of the biological oxygen demand and the dissolved oxygen for freshwater treatment are governed by partial differential equations
2. The outfalls are located at points
3. The convex functions are known
4. The fluid medium is continuous.
5. The soil matrix is continuous.
6. The fluid is in mot ion.
7. The soil medium undergoes consolidation.
8. The fluid is incompressible.
9. The air phase is continuous and is at atmospheric pressure.
10. Flow is laminar and Darcy’s law is valid.
The biological oxygen demand and dissolved oxygen concentrations in a point u and a time t be denoted by ρ1(u,t) and ρ2(u,t) respectively .The boundary equations can be obtained by
Considering the following boundary value problems
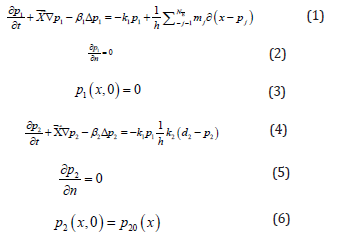
Let h(u,t) and x ⃗(u,t) be the height and the mean horizontal velocity of the fluid layer obtained as a solution of saint venant equation. ∂(x-p_J) is the dirac measure for point p_i and the parameters β1> 0, β2 >0 represents the horizontal viscosity coefficients involving the dispersion and turbulence effects. Parameters k1> 0, k2 >0 represents the kinetic coefficients related to temperature and transference of oxygen through the surface and ds is the oxygen saturation density which can be drawn from experimental measurements.
Let the existence inside the domain Q of Nz protected zones Ai be
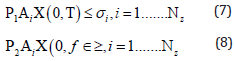
The global cost of the depuration time is given by
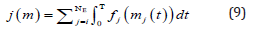
There is need to ascertain the optimal management of the depuration system by taking into cognizance the values of the biological oxygen demand m_j(t) >0, j=1…., NE throughout the time interval. Numerical approximation of the state system. Unwinding the convective term with a method of characteristics and by discretizing in time the partial differentiation would give rise to a numerical resolution of optimal control problem. The variational formulation of semi discretized problem will be approximated by means of a space discretization of lagrange-Galerkin finite elements. There is need to consider the following parameters when solving discretized problems. The parameters include: The approximated height h, horizontal mean velocity x ⃗ for each discretized time, discontinuous piecewise-constant (p_Θ) functions and piecewiselinear( p_1)
Polynomials the method of characteristics stems from the following inequality
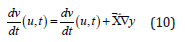
Where is the total derivative of v with respect to time t and
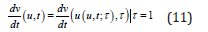
The characteristic line is a unique solution to the following differential equation
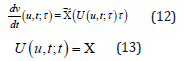
For time interval [0, T], the total derivative of v at any instant t_(n+1) can be approximated as
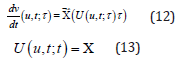
This equation leads to the following semi discretized models for each n=1,…N, there is need to ascertain functions ρ1n, ρ2n satisfying
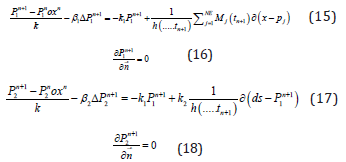
The exact solution of the quasi-linear partial differential equations [Eqs 17 and 18] subject to the initial [Eq. 16] and boundary [Eqs. 17and 18] conditions is generally not possible. Consequently, recourse to approximate solution techniques is required.
Finite Element Formulation
The first step in the numerical approximation of the quasi-linear partial differential equations is to choose the discretization strategy. This investigation is based on using a finite element discretization. Finite elements were chosen due to its ability to model irregular boundaries, mesh refinement/expansion capabilities and the ease in modelling complicated boundary conditions. The finite element discretization/formulation involves three basic steps, i.e., (1) Development of an integral relationship corresponding to the governing differential equation, (2) Definition of the element geometric forms and (3) Approximation of the unknown field variable. In this investigation, the weak Galerkin weighted residual method is used to construct the finite element integral equations. Iso-parametric quadratic triangular and quadrilateral finite elements are used to represent the flow domain and the field variable variation.
Galerkin Formulation
The Galerkin finite element formulation begins with defining the governing differential equation as
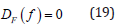
Where f signifies the pressure head h for Eq. [19] and the moisture content 9 for Eq. [20]. The next step in the Galerkin formulation is to approximate the field variable behavior, i.e.,
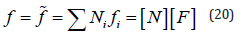
Where [N] is a row vector of shape and [f] is the column vector containing the nodal values of the appropriate field variables. Substituting f from Eq. [20] into the differential operator of Eq. [21]
Gives:
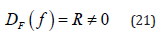
where R is the residual. If the exact solution f and the approximate solution f ⃗ are the same, then the residual of Eq. [21] would be zero. However, the approximate solution does not generally equal the exact solution resulting in the nonzero residual indicated in Eq. [23] Since the governing differential equation cannot be satisfied point wise throughout the domain ll, its satisfaction is sought in the sense of a weighted average over the domain
i.e.,
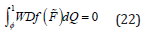
where W is the weighting function. In the finite element Galerkin formulation, the weighted integral of Eq. [24] is summed over all the· element subdomains Qe and the element level shape functions are utilized as the weight functions, i.e.,
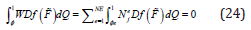
For j=1,2…., ne
Where N^e is the number of elements used to discretize the domain Q, N_j^e is the Jith is the shape function for element e, n_e is the number of element shape functions. The Galerkin formulation of Eq, III,5 possesses the disadvantages of requiring cl interelement continuity (i.e., first derivative continuity between the elements), exact satisfaction of all boundary conditions and leads to a non-symmetric system of equations. These disadvantages can be relaxed or eliminated by generating a ‘weak’ Galerkin formulation of Eq,[25]. The weak Galerkin formulation is obtained by integrating Eq,[26] by parts once using the divergence theorem to symbolically give:
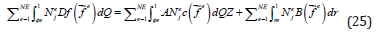
For j=1,2…., ne
The result of Eq,[26] for the pressure analysis [27] is
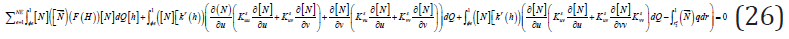
and for the moisture content analysis [27] it is
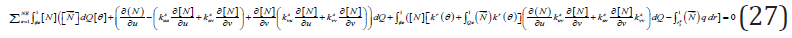
Where the superposed dot signifies time differentiation and ([N) ⃗] is the vector of element shape functions evaluated along the flux loaded element boundaryΓ_2^e. The nonlinear material coefficients F(h), k^Γ(h),Dr(θ) and k^Γ(θ) were spacially approximated using interpolation functions.
Scrutinizing Eqs. [26] and [27] reveals the modifications of the weak Galerkin versus Galerkin formulations. First, the shape functions need only be c0 inter-element continuous, i.e, function continuity between the elements. Second, the vector products which multiply the pressure and moisture content vectors are symmetric which results in a symmetric system of equations. Lastly, only the boundary conditions given by Eqs[28] and [29] must be exactly satisfied since the flux or flow boundary conditions of Eqs. [28] and Eqs[29] are included in the discretized approximation. Where Eqs. [28] And [29] can be written in matrix form
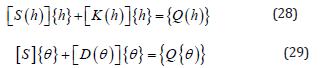
Where,
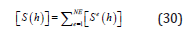
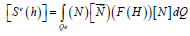 element storage matrx
element storage matrx
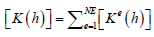 pressure dependent conductivity flow matrix.
pressure dependent conductivity flow matrix.
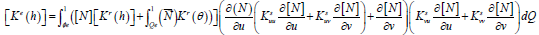 element conductivity matrix
element conductivity matrix
The quadratic triangular and quadrilateral elements of were selected. The shape functions for the six node triangle element are expressed in terms of non-dimensional coordinates known as area coordinates. The area (local) coordinate shape functions are:
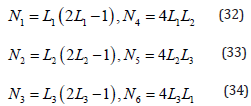
Where the element nodes and area coordinates (O ≤ L1, L2, L3 ≤1). The three area coordinates are not independent. Thus, in order to utilize an iso-parametric formulation of these shape functions, the coordinate dependence must be removed. The coordinate dependence is easily eliminated by substituting
L3=L-L1-L2 into Eq. [34]. The eight-node element are:
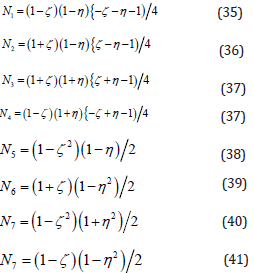
The material parameter interpolation functions, {N}, were assumed to be linear. Thus, for the triangular element
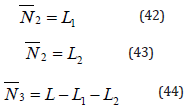
and for the quadrilateral element:
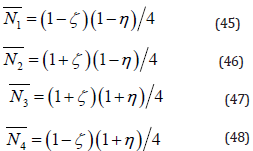
Results and Discussion
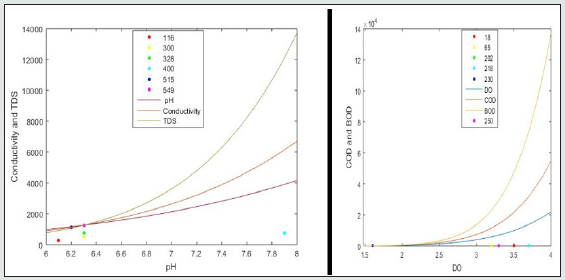
The pH values for samples A, B, C, D and E for both influent and effluent were varied with different parameters affecting wastewater treatment. The mean average pH values for wastewater according to the Table 1 were found to lie between 5.94 and 6.71 at distances 5m and 10m away from point of discharge. From the results obtained, industrial discharge and other pollution sources increased the pH values of the water as seen in Figures 1a, 2a, 3a, 4a and 5a.The electrical conductivity were also varied between 571 and 961μS.m-1. The effluent discharge increased the electrical conductivity of wastewater as seen in Figures 1a,2a,3a,4a and 5a, therefore indicating the impact on receiving water. TDS and DO were also varied in order to deduce their influent concentrations. From Figures 1b, 2b, 3b, 4b and 5b. TDS lied in-between 280 and 460mg.L-1 and DO vary at 2.3 mg.L-1 respectively. For instance, obtained mean concentration values for BOD, 194 and 152.7 mg.LG1 at influent and effluent respectively indicates 53% purification level in respect of BOD. Even with this level of performance, BOD concentrations are still extremely high in effluent, varying between 115 and 182 mg.lG1. The removal efficiencies for the following measured parameters during the dry season stand at 44% for TDS, 44% for BOD, 29% for COD and 32% for N. The removal efficiencies during different seasons for TDS, BOD, COD and N stand at 16, 63, 55.8 and 72% respectively. From the results of pollution assessment of wastewater, it is revealed that the receiving river body has been impacted negatively [22,23].
Table 1: Physio-chemical characteristics of influent and effluent during wet seasons for sample A, B, C D and E [22].
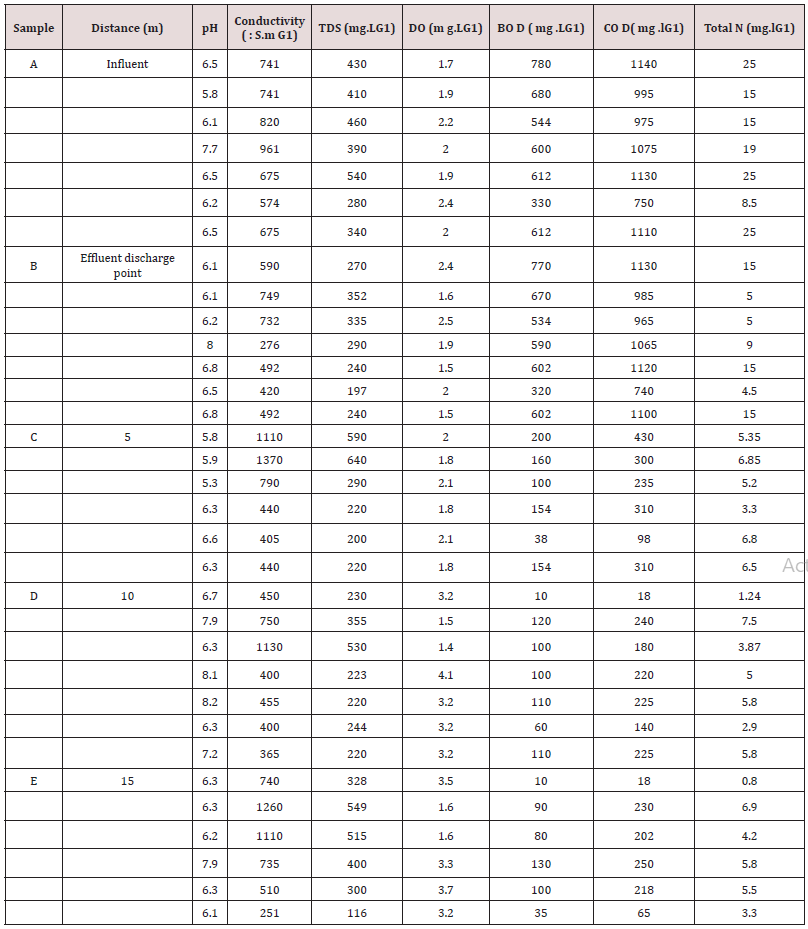
Figure 1(a & b): Graph of Physio-chemical characteristics of influent and effluent during wet seasons for sample A for COD and BOD.
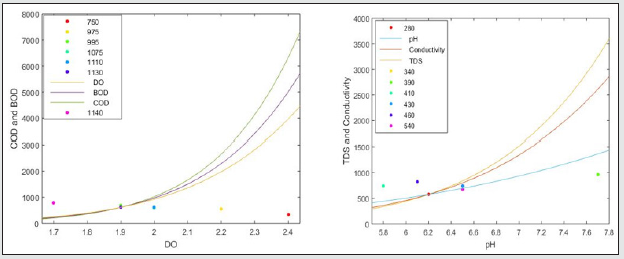
Figure 2(a & b): Graph of Physio-chemical characteristics of influent and effluent during wet seasons for sample B for COD and BOD.
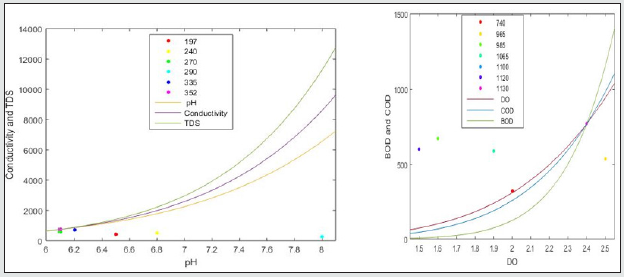
Figure 3(a & b): Graph of Physio-chemical characteristics of influent and effluent during wet seasons for sample C for COD and BOD.
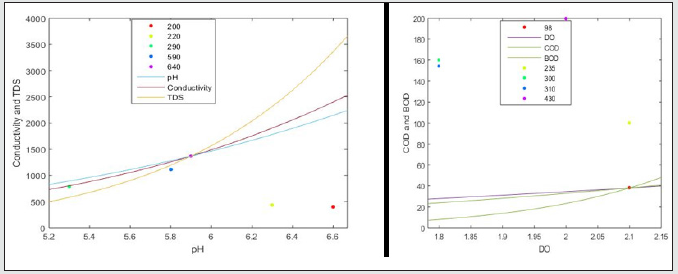
Figure 4(a & b): Graph of Physio-chemical characteristics of influent and effluent during wet seasons for sample D for COD and BOD.
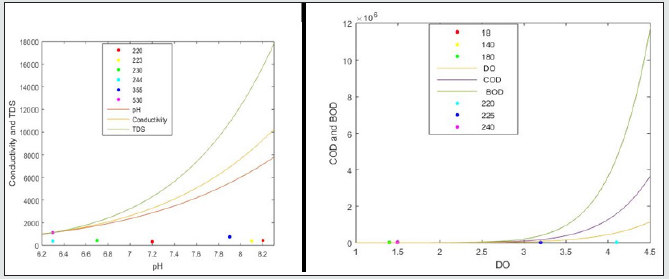
Figure 5(a & b): Graph of Physio-chemical characteristics of influent and effluent during wet seasons for sample D for COD and BOD.
Conclusion
In the study, the increment in number of wastewater treatment plants, has made it difficult to manage the wastewater systems. Therefore, to ensure proper discharge from the wastewater treatment plants, new and stricter regulations for nutrient removal have to be incorporated. Several wastewater treatment measures that have been adapted to date includes bio filtration, ion exchange, sedimentation, solvent extraction, chemical oxidation, membrane processes, coagulation, oxidation, Fenton process, and electro coagulation. Adsorption is today regarded as the best water treatment procedure because of its universal nature, ease of operation and inexpensiveness.it has a removal capacity rate of 99.9%. The adsorption has some limits which made its removal rates not to perfect. To comply with these limits, there is a need for modeling and operation control of wastewater treatment plants. However, the modeling of wastewater treatment systems tends to become intricate due to certain characteristics such as unusually long residence times, plenty of tunable kinetic parameters and large variations in influent component flow rates. The removal efficiencies during the wet season for TDS, BOD, COD and N stand at 16, 63, 55.8 and 72% respectively. From the results of pollution assessment of wastewater, it is revealed that the receiving river body has been impacted negatively.
References
- M M Manyuchi, C Mbohwa, E Muzenda (2018) Utilization of Agro waste Bio Adsorbents in Textile Wastewater Treatment. Proceedings of the International Conference on Industrial Engineering and Operations Management Pretoria / Johannesburg, South Arica.
- M Shafiq, A A Alazba; M T Amin (2018) Removal of Heavy Metals from Wastewater using Date Palm as a Biosorbent: A Comparative Review. Sains Malaysiana 47(1): 35-49
- Neethu P, M A Chinnamma (2017) Natural Adsorbents for Agricultural WasteWater Treatment. International Journal of Advanced Engineering, Management and Science (IJAEMS) 3(4).
- Md Shak Sadi, Burhan Uddin Banna, Kazi Md Hasanul Haque, Md Bright Bin Abdullah, Md Mosfaqur Rahman Khan, et al. (2018) Natural Adsorbents; an Eco-Friendly Solution for the Removal of Ph, Tds, Do, Bod & Color from the Textile Effluent.
- Grégorio Crini, Eric Lichtfouse (2018) Wastewater treatment: an overview. Green Adsorbents for Pollutant Removal Springer Nature pp: 1-22.
- Nadia Morin Crini, Eric Lichtfouse, Giangiacomo Torri, Grégorio Crini (2019) Applications of chitosan in food, pharmaceuticals, medicine, cosmetics, agriculture, textiles, pulp and paper, biotechnology, and environmental chemistry. Environmental Chemistry Letters Springer Verlag 17(4): 1667-1692.
- F Ben Rebah, S M Siddeeg (2017) Cactus an eco-friendly material for wastewater treatment: A review. Journal of Materials and Environmental Sciences ISSN: 2028-2508 8(5): 1770-1782.
- Upendra Kumar (2006) Agricultural products and by-products as a low-cost adsorbent for heavy metal removal from water and wastewater: A review. Scientific Research and Essay 1(2): 033-037.
- Imran Ali, Mohd Asim, Tabrez A Khan (2012) Review. Low-cost adsorbents for the removal of organic pollutants from wastewater. Journal of Environmental Management 170: e1830301-4797.
- Mr Rajesh Bhagat, Dr Shantanu Khandeshwar (2019) A Synoptic Review on Composite Adsorbents to Remove Heavy Metals from Industrial Wastewater. Impact Factor Value 4.046 e-ISSN: 2456-3463 National Conference on "Recent Advances in Engineering and Technology" Sammantrana 19 Organized by Government College of Engineering, Nagpur International Journal of Innovations in Engineering and Science 4(8).
- T C Mokhena, V Jacobs, A S Luyt (2015) A review on electrospun bio-based polymers for waterTreatment. eXPRESS Polymer Letters 9(10): 839-880.
- D S Malik, C K Jain, Anuj K Yadav (2017) Removal of heavy metals from emerging cellulosic low-cost adsorbents: a review. Appl Water Sci pp: 2113-2136.
- Muhammad Rahim, Mas Rosemal Hakim Mas Haris (2015) Application of biopolymer composites in arsenic removal from aqueous medium: A review. Journal of Radiation Research and Applied Sciences 8(2): 255e263.
- Peter Adeniyi Alabaa, Nurudeen Abiola Oladojac, Yahaya Mohammad Sanid, Olumide Bolarinwa Ayodelee, Isah Yakub Mohammed f, et al. (2018) Insight into wastewater decontamination using polymeric adsorbents. Journal of Environmental Chemical Engineering 6(2): 1651-1672.
- Olafadehan O A, Abhulimen K E, Adeleke A I, Njoku C V, Amoo K O (2019) Production and characterization of derived composite biosorbents from animal bone. African Journal of Pure and Applied Chemistry 13(2): 12-26.
- Kumari Shweta, Harit (2016) Jha Synthesis and characterization of crystalline carboxymethylated lignin-TEOS nano composites for metal adsorption and antibacterial activity.
- B O Opeolu, O Bamgbose, T A Arowolo, M T Adetunji (2010) Utilization of biomaterials as adsorbents for heavy metals’ removal from aqueous matrices. Scientific Research and Essays 5(14): 1780-1787.
- Jatindra N Bhakta, Yukihiro Munekage (2009) Ceramic as a Potential Tool for Water Reclamation: A Concise Review. Journal of Environmental Protection Science 3: 147-162.
- S Álvarez Torrellas, J A Peres, V Gil Álvarez, G Ovejero, J García (2017) Effective adsorption of non-biodegradable pharmaceuticals from hospital wastewater with different carbon materials. Chemical Engineering Journal 320: 319-329
- J Kandasamy, S Vigneswaran, T T L Hoang (2017) Adsorption and Biological Filtration In Wastewater Treatment. Water and Wastewater Treatment Technologies - Adsorption and Biological Filtration in Wastewater. Water And Wastewater Treatment Technologies.
- Mohsen Dehghani, Mohammad Hossein Alizadeh (2016) The effects of the natural coagulant Moringa oleifera and alum in wastewater treatment at the Bandar Abbas Oil Refinery. Environmental Health Engineering and Management Journal 3(4): 225-230
- E O Longe, A O Ogundipe (2010) Assessment of Wastewater Discharge Impact from a Sewage Treatment Plant on Lagoon Water, Lagos, Nigeria. Research Journal of Applied Sciences, Engineering and Technology 2(3): 274-282.
- Misikir Tamiru, Gabisa Bekele (2020) Various Absorbents and Parameters Affecting Removal of Water Hardness from Wastewater: Review. International Journal of Water and Wastewater Treatment ISSN 2381-5299.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...





