Theoretical Feasibility Research on 3D Printing Technology Applied to Statics Model Experiment Volume 1 - Issue 3

Zhiwei Zhang and Jinsheng Sun*

• School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China

Received: August 06, 2020   Published: October 19, 2020

Corresponding author: Jinsheng Sun, School of Chemical Engineering and Technology, Tianjin University, Tianjin 300072, China

DOI: 10.32474/JOMME.2020.01.000114

 

Abstract PDF

Abstract

3D printing is effective to manufacture experimental models widely used in analogous statics tests before practical engineering applications. Whereas, traditional statics model experiments with strict dimensionless function are hardly to be established through 3D printing items according to similarity theory. To find a solution, this paper theoretically simplifies the statics system based on reducing constrains of weight and Poisson’s ratio. This simplification is the core of a new method of additional weight and correction to identify the simplified and the original statics systems. Operation procedures are displayed through case studies using the new method. 3D printed materials for specific statics experiments are validated as well through coefficient corrections. The results will finally contribute to 3D printing technology applied to analogic static research, for not only academic but also industrial purposes.

Keywords: 3D printing; Statics model experiment; Similarity theory; Coefficient corrections

Introduction

Scale test also known as model experiment is an effective tool to simulate and investigate phenomena, which can’t be established directly [1-2]. Based on dimensional analysis and similarity theory, the similarity criteria can be formulated mathematically to obtain equivalent relationships between prototype and model [1-3]. Actually, the technique has been flourishing in applications of statics [4-8], hydromechanics [1,2, 9] and energy field [10-11]. Among them, statics model experiment is widely used to verify designs before on-site engineering for academic and designing purposes. However, traditional modeling has troubles in making complex structure as a whole in only one step. And then the indispensable post-treatments will change the state of stress, resulting in experimental errors, even at the cost of rocket high expenditure and large human labor amount. This step undermines the benefit from cheap substitution materials and reduces the efficiency of the whole optimization process.
Contrary to traditional modeling, 3D printing can detours all the above drawbacks through directly making complex geometries in one step, such as models, assembly fixtures and production molds. It is more flexible in design and fabrication of parts than traditional machining techniques [12-13]. In fact, Chandra Sekhar Tiwary et al. have used macroscale 3D printing models to analogically investigate the mechanical behavior of molecular schwartzite structures [14]. Obviously, 3D printing is potentially the best tool for statics model experiments, as it has performed well in not only industrial applications but also scientific research in the past 4 decades. It displays talents in multiple fields, such as supply chain [13,15-16], synthesis chemistry [17-20], chemical engineering [21- 26], bionics or biology [27-28], orthopedics or medicine [29-32], mechanics [33-34], optics [35], electrics [36] and even arts [37-38].
However, the accuracy and the reliability of statics model experiments strictly depend on theoretically mathematical equations [1-2]. In detail, in form of the π theorem, it enables an object or a system to be represented by a dimensionless similarity function of dimensionless parameters (π values) [1-4]. That is, objects or systems are considered completely similar for the same dimensionless parameters (π values) [1-4]. Whereas, traditional statics model experiments with strict dimensionless function are hardly to be established through 3D printing items. In other words, 3D printing statics model is restricted by printing material and scale or size of the model. Even though 3D printing materials satisfy the requirements for balancing system, too large or too small model is difficult to be built and directly used in static experiments for poor practicability and operability [1-2, 6-7], such as limited 3D printing device and test equipment. Thus, it is necessary to establish a method to make 3D printed models customized for actual testing purpose equivalent to the prototype in detailed structure and static indexes as stress, strain and displacement [6-8]. In fact, some studies have been carried out to solve above problems. Murphy proposed a strategy to relax the similarity constraints by intentionally casting the prediction equation into the more complex form [39]. Kristin L.Wood et al. provided an improved similarity method that utilizes a geometrically simple specimen pair, in order to design the prototype with more freedom [40].
To make it feasible, this paper reduces the internal constraints of the statics structural system. That is, the dimensionless similarity function is theoretically simplified based on reducing constrains of weight and Poisson’s ratio, so as to loosen the limits to 3D printing model materials. The method is interpreted through popular cases in detail,when different material and Poisson’s ratio encountered between 3D printed model and prototype. The validated pathway will methodologically benefit and enhance the accuracy of statics researches through 3D printing model experiments.

Theoretical simplification

Compensation method without gravity

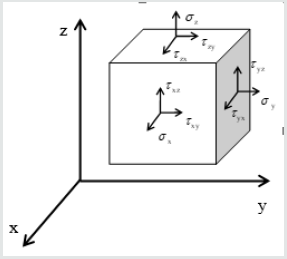
According to similarity theory or π theorem [1-4], a statics equilibrium system must satisfy a dimensionless equation. Thus, all constraint equations defining elastic microelement are investigated to make clear the physical meaning of dimensionless parameters and make general the proposed method. These definition equations are composed of equilibrium equations, geometric equations, constitutive equations and boundary conditions, individually expressed by Eq. (1) to Eq. (5). Eq. (4) represents boundary condition of displacement and Eq. (5) boundary condition of stress and surface force. The elastic microelement of statics structure is shown in Figure 1. The x axis forwards in the same direction as the acceleration of gravity.

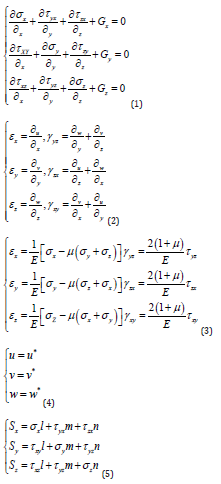
The similarity ratio Cx is defined as the ratio of the correspondent physical quantities of the prototype to the corresponding model, with the subscript x represents the homologous physical quantity. For example, is the geometric similarity ratio between lengths. Considering all constraint equations with three sub-equations in the same form, one of them can represent whole related constraint equation. Hence, equilibrium equations for prototype and model can be individually expressed, as Eq. (6) the model equilibrium equation and Eq. (7) the prototype equilibrium equation:

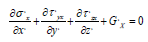(6)

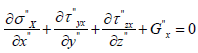(7)

ratios, as followsEq. (7) can be replaced by similarity:

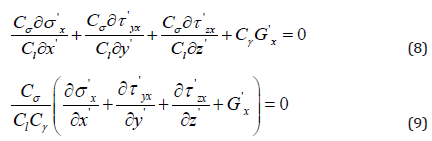
Then the first similarity criterion equation can be obtained by Eq. (6) and Eq. (9), as follows:

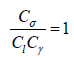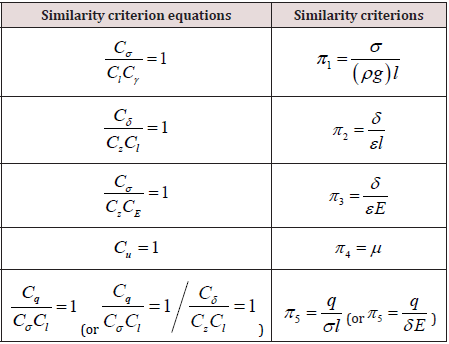
(10)

Similarly, the other similarity criterion equations can be obtained based on Eq. (2) to Eq. (5), as follows:

Eq. (14) can also be deducted from distributed force, concentrated force Zor bending moment M, with distributed force considered in this paper. Therefore, Eq. (14) can be transformed into Eq. (15). According to above similarity criterion equations, corresponding similarity criterions or dimensionless parameters are summarized in Table 1. In order to simplify subsequent analyses, new dimensionless parameters π_5 can be changed by means of taking ratio π_5 to π_2, also shown in Table 1. Regardless of prototype or model statics structures, both have the same dimensionless equation (16). Since the accuracy of the strain is determined by measurement device, the available similarity ratio of strain falls into a certain range for the sake of precise when using the same measurement device. Herein is defined as. If Poisson’s ratios of the prototype and the model materials are the same, there will be anunique statics model experiment. Furthermore, when scale of model is given, the model material must have same. However, both the above conditions are very hard to be satisfied. Obviously, the strict dimensionless equation becomes an obstacle. That is, Eq. (16) needs to be simplified to release the limits.

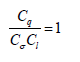(15)

(16)

First, the structure weight is regarded as an external force or load. Eq. (1) is then replaced by Eq. (17), with no similarity criterions obtained. If Poisson’s ratio is also not considered, the dimensionless equation of statics structure is transformed into Eq. (18). Certainly, compensation and correction are necessary to ensure equivalence of model experiments. Compared with the statics system of Eq. (16), the new Eq. (18) develops two more degrees of freedom. In other words, model experiment can be customized to satisfy actual application, exemplified below. (Of course, the above deduction process can also be performed based on Buckingham Π theorem, but there are difficulties to understand and expound the natural meanings of physical process).

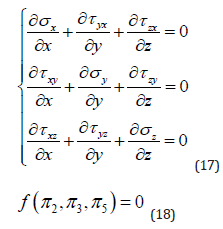
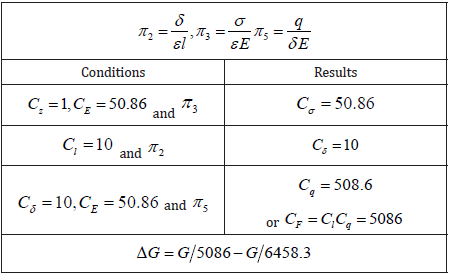
Polylactic acid (PLA), widely used 3D printing material, is selected for the model to investigate a prototype in Q345R (16Mn), one of the most common engineering materials. The parameters of the two materials are summarized in Table 2 [41]. The calculation procedure is summarized in Table 3 for similarity ratio of simplified statics system. In Table 3, changeable may as well assigned to be.

Taking gravity as force, similarity ratio of gravity in above case is equal to similarity ratio of concentrated force, or. Actually, the ratio of prototype weight to model weight is. This means the model weight is reduced and an additional weight calls for compensation, with G the weight of prototype, evenly loaded of course.

Method for inequivalent Poisson’s ratio

Material Poisson’s ratio of the 3D printed model are likely different from that of the prototype, resulting in inaccurate prediction. This calls for a method dealing within equivalent Poisson’s ratios to ensure overall equivalence of model experiments or no constraint for 3D printing application in economic testing materials.
Apparently, for model and prototype materials with the same material Poisson’s ratios, both of targets possess same dimensionless parameters or dimensionless similarity Eq. (18). Otherwise, model experiment should meet:

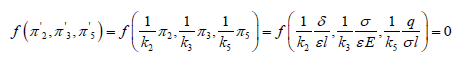(19)

where correction coefficient is used to revise dimensionless parameters of 3D printing model. According to Eq. (18) and Eq. (19), the mathematical expression Eq. (20) for correction coefficient is obtained.

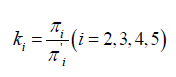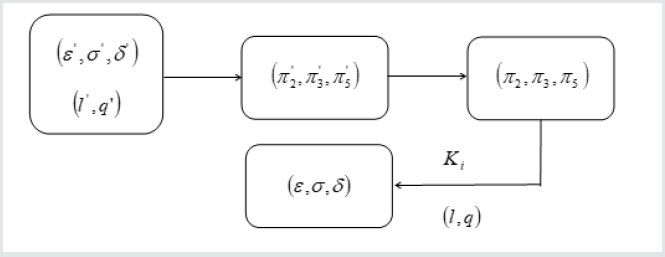
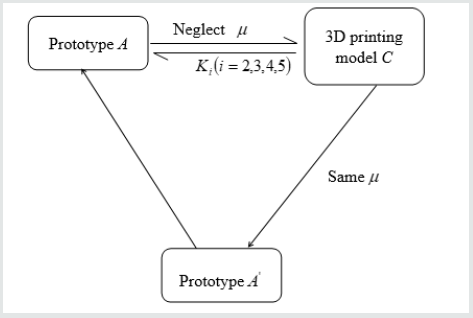
(20)

Therefore, prediction can be provided in Figure 2, of the 3D printing model experiment to substitute for the prototype one. The prototype is herein defined as A, model with same Poisson’s ratios as B and model made by 3D printing as C. The dimensionless parameters can be obtained based on the state of a known point, regardless of prototype or model structures. In Figure 2, of model C can be obtained from of a known point and Thus, for prototype A or model B can be calculated by Eq. (20). Then of the corresponding point can be obtained by combing corresponding and.

In Figure 2, the correction coefficient must be given between model C and B or prototype A. Nevertheless, model experiment of B and C must be conducted in the light of definition of correction coefficient. This paradox makes the correction coefficient meaningless and unnecessary. To jump out, computer simulation is considered to take the place of the actual model experiment. More and more advanced and reliable, simulation results sometimes can be directly used for engineering and scientific purposes. Especially, it works pretty well for the structure with the clear mathematical models or constitutive relations. As a matter of fact, computer simulation is not conflict with model experiment, but complementary with each other. Firstly, the computer simulation results can completely replace the experiment for the known field of mechanics theory; And the result is more reliable than the experimental results, to some extent. But the computer simulation can’t perfectly reflect the details of the mechanical response, especially the loading process and the structural damage.

According to Figure 2, two computer simulation experiments are required, and the 3D print model experiment needs a proportional conversion. Although the correction coefficient can be calculated, the above calculation process is still very troublesome. Therefore, the analysis of Fig. 3 simplifies the simulation process. 3D printing model C is established on the basic of simplified statics system. 3D printing model C can equivalently study prototype A by means of adjusting correction coefficient. In addition to same Poisson’s ratio, prototype is established depending on same similarity ratio as above process. Thus, 3D printing model and prototype possess same dimensionless parameters or dimensionless similarity Eq. (19). At this stage, Except for Poisson’s ratio, Prototype A and prototype is identical. Then the correction coefficient between 3D printing model C and prototype A can be found by simulating prototype A and prototype. In other words, the correction coefficient is available by regression or trail of the prototype Poisson’s ratio with the aid of computer. Furthermore, the impact can also be studied of different 3D printing materials on static prediction results through the establishment of curve. If so, the appropriate 3D printing material can be chosen for specific statics experiment.

Case analysis of correction coefficient

For simplified statics system, methods of compensation and correction ensure equivalence of modelexperiments, assisted by additional weight available through case study. Similarly, method for inequivalent Poisson’s ratio is herein expound in detail by means of a specific case analysis.
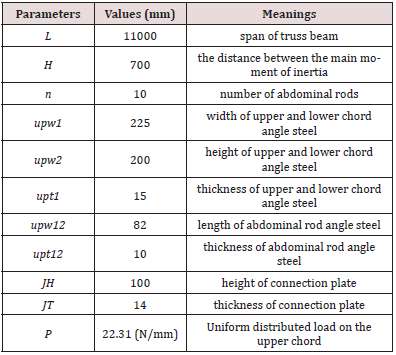
The truss beam is selected in the large column as the object of computer simulation, shown in Figure 4 [42]. Obviously, any simple statics structure here can be used to illustrate the point of the paper. Geometric parameters and load of prototype are summarized in Table 4. Properties of prototype material subjected to working conditions are summarized in Table 5. The point of measurement is recommended to select the one where stress and strain are easy to converge. Therefore, the point is the best candidate near the axis of left-and-right symmetry on truss beam. Then the simulated results of the deformation, stress and strain of the selected points are summarized in Table 6.

According to Eq. (18), Eq. (19), Eq. (20) and Figure 2, the calculation process of correction coefficient is shown as follows in Eq. (21), where denominator represents the dimensionless parameters of the prototype structure and the numerator represents the model one.

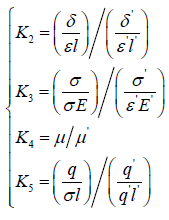(21)

Obviously, the value of l and q is equal to l' and q' , individually. So, the Eq. (21) can be transformed into Eq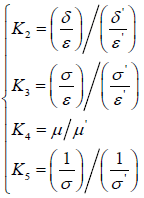. (22),

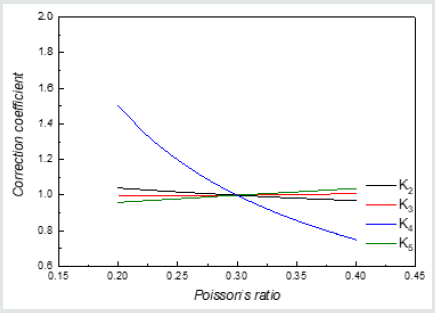
(22)

Combining with Eq. (22) and Table6, the results of correction coefficient can be summarized in Table 7 and Fig.5 under different Poisson’s ratio. Fig.5 can show the changing trend of the correction coefficient of this truss structure with Poisson’s ratio better.

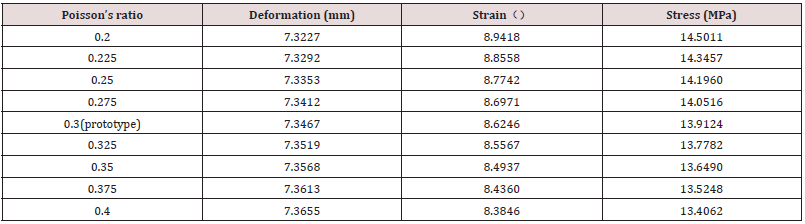
After correction coefficient is obtained, prediction process in Fig.2 can be carried out. Then 3D printing model experiment can be applied to the simplified statics system without obstacles. Actually, correction coefficient revises stress, strain and deformation of 3D printing model experiment. Further, the calculated correction coefficients can modify the relative similarity ratio, so that the calculation process of 3D printing model experiment for prototype prediction is more convenient. Mathematical expressions are displayed in Eq. (23). This method can not only obtain the corresponding correction coefficient, but also study the the influence of Poisson’s ratio on the statics system.

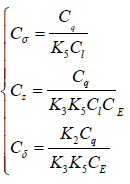(23)

Conclusion

This work simplifies statics system on the basis of theoretical analysis. To guarantee equivalence of 3D printing model experiment, weight compensation and correction are proposed of dimensionless parameters through treating weight as external applied load. Correction coefficient is calculated by computer simulation for correction of dimensionless parameters. Essentially, the correction coefficient is a modification to the stress, strain and displacement, resulted from different Poisson’s ratio between 3D printing material and prototype material. After relevant case analyses, the method is validated and illustrated. This proves the theoretical feasibility of 3D printing to be applied to static model experiment under similarity theory with different module size and materials. Obviously, the research method is strictly applicable in prediction for the elastic behavior. It can be also used to qualitatively analyze the mechanical behavior of breaking stage through 3D printing scale test. Generally speaking, the methodology will benefit analogical statics investigations in the age of 3D printing.

References

1. Howarth L (1960) "Front Matter - Similarity and Dimensional Methods in Mechanics". Physics Bulletin 11(6): 168.
2. Yalin M Selim (1971) "Theory of Hydraulic Models" Macmillan Civil Engineering Hydraulics”.
3. Rudolph Stephan (2009) "Mathematical Foundations of Non-Classical Extensions of Similarity Theory". IUTAM Symposium on Scaling in Solid Mechanics, Springer, Netherlands p. 27-35.
4. Ma Qin‐Yong, M Cai (2003) "Determination of Similarity of Explosives for a Model Experiment." Combustion Explosion & Shock Waves 39: 606-609.
5. Zhe Li, Gongxian Wang, Jiquan Hu (2014) "Predictive Coefficient Method for Establishing Similarity Model of Jumbo Container Cranes." International Conference on Vibration Engineering & Technology of Machinery Vetomac X 2014 September 9-11, 2014 University of Manchester, Uk: 901-914.
6. Li, Yong, YX Wang (2015)"Static Model Experiment Study on a Concrete-Filled Steel Tubular Arch Bridge." Key Engineering Materials 648: 61-71.
7. Ma, Hai Chun, KR Cui, FS Zha (2014) "The Dimensional Analysis and Similar Theory of Model Tests for Explosion Resisting Capacity of Tunnels." Applied Mechanics & Materials 488-489: 666-668.
8. Ju, Seok Nam, et al. (2014) "Application of similarity theory to load capacity of gearboxes." Journal of Mechanical Science & Technology 28(8): 3033-3040.
9. Zhang M, P Vardcharragosad, FAHL (2014) "The similarity theory applied to early-transient gas flow analysis in unconventional reservoirs." Journal of Natural Gas Science & Engineering 21: 659-668.
10. Xu, Guoqiang, et al. (2015) "The application of similarity theory for heat transfer investigation in rotational internal cooling channel." International Journal of Heat & Mass Transfer 85: 98-109.
11. Jin, Jian, Y Ling, Y Hao (2017) "Similarity analysis of parabolic-trough solar collectors." Applied Energy 204: 958-965.
12. Edgar, Jonathan, Tint (2015) "“Additive Manufacturing Technologies: 3D Printing, Rapid Prototyping, and Direct Digital Manufacturing”, 2nd Edition." Johnson Matthey Technology Review 59(3):193-198.
13. Macdonald, E, R Wicker (2016) "Multiprocess 3D printing for increasing component functionality." Science 353(6307): aaf2093-aaf2093.
14. Sajadi, Seyed Mohammad, et al. (2017) "Multiscale Geometric Design Principles Applied to 3D Printed Schwarzites." Advanced Materials.
15. Eckes Felix (2016) "Impact of 3D Printing on Supply Chain Relationships: A Study within the German Automotive and Logistics Sector." MS Thesis, Jonkoping University p. 58.
16. Johnson, James A (2014) "3D Printing -- The New Industrial Revolution: Innovation or Infringement." Social Science Electronic Publishing 43(1).
17. Kitson, Philip J, et al. (2016) "3D printing of versatile reactionware for chemical synthesis." Nature Protocols 11(5): 920-936.
18. Kitson, Philip J, et al. (2013) "Combining 3D printing and liquid handling to produce user-friendly reactionware for chemical synthesis and purification." Chemical Science 4(8): 3099-3103.
19. Capel AJ (2013)"Design and additive manufacture for flow chemistry. " Lab on A Chip 13(23): 4583.
20. Gong H, AT Woolley, GP Nordin(2016) "High density 3D printed microfluidic valves, pumps, and multiplexers." Lab on A Chip 16(13): 2450.
21. Poppell, Samuel W, et al. (2013) "3D printing for CO2 capture and chemical engineering design." Nanomaterials & Energy 2(5): 235-243.
22. Couck, Sarah, et al. (2017) "CO2, CH4 and N2 separation with a 3DFD-printed ZSM-5 monolith." Chemical Engineering Journal 308: 719-726.
23. Hwang, Yongha, OH Paydar, and RN Candler (2015) "3D printed molds for non-planar PDMS microfluidic channels." Sensors & Actuators A Physical 226: 137-142.
24. Mardani, Saeed, et al. (2016) "Development of a unique modular distillation column using 3D printing." Chemical Engineering & Processing Process Intensification 109: 136-148.
25. Fee, CS Nawada, S Dimartino(2014) "3D printed porous media columns with fine control of column packing morphology. " Journal of Chromatography A 1333(5): 18-24.
26. Mcdonough, JR, et al. (2017) "Effect of geometrical parameters on flow-switching frequencies in 3D printed fluidic oscillators containing different liquids." Chemical Engineering Research & Design 117: 228-239.
27. Dalaq, Ahmed S, DW Abueidda, RKA Al-Rub (2016) "Mechanical properties of 3D printed interpenetrating phase composites with novel architectured 3D solid-sheet reinforcements." Composites Part A Applied Science & Manufacturing 84: 266-280.
28. Tiwary, Chandra Sekhar, et al. (2015) "Morphogenesis and mechanostabilization of complex natural and 3D printed shapes." Science Advances 1(4).
29. Wang, Kan, et al. (2016) "Dual-material 3D printed metamaterials with tunable mechanical properties for patient-specific tissue-mimicking phantoms." Additive Manufacturing 12: 31-37.
30. Tamjid, E, and A Simchi (2015) "Fabrication of a highly ordered hierarchically designed porous nanocomposite via, indirect 3D printing: Mechanical properties and in vitro cell responses." Materials & Design 88: 924-931.
31. Sandstrom, Christian G (2016) "The non-disruptive emergence of an ecosystem for 3D Printing- Insights from the hearing aid industry's transition 1989–2008." Technological Forecasting & Social Change 102: 160-168.
32. Murr, Lawrence E, et al. (2012) "Metal Fabrication by Additive Manufacturing Using Laser and Electron Beam Melting Technologies." Journal of Materials Science & Technology 28(1): 1-14.
33. Moon, Seung Ki, et al. (2014) "Application of 3D printing technology for designing light-weight unmanned aerial vehicle wing structures." International Journal of Precision Engineering and Manufacturing-Green Technology 1(3): 223-228.
34. Smith CJ, et al. (2016)"Dimensional accuracy of Electron Beam Melting (EBM) additive manufacture with regard to weight optimized truss structures." Journal of Materials Processing Tech 229: 128-138.
35. Chanda D, et al. (2011) "Large-area flexible 3D optical negative index metamaterial formed by nanotransfer printing." Nature Nanotechnology 6(7): 402-407.
36. Isakov DV, Lei Q, Castles F, Stevens CJ, Grovenor CRM, etal. (2016) "3D printed anisotropic dielectric composite with meta-material features." Materials & Design 93: 423-430.
37. Zhang Xiaolong, yang Xia, Jiayewang, Zhouwang yang, ChangheTuetet al. (2015) "Medial axis tree-an internal supporting structure for 3D printing." Computer Aided Geometric Design 35-36: 149-162.
38. Ezair Ben, F Massarwi, G Elber, (2015)“Orientation analysis of 3D objects toward minimal support volume in 3D-printing”. Pergamon Press 51: 117-124.
39. Murphy Glenn (1971) "Models with incomplete correspondence with the prototype." Journal of the Franklin Institute 292(6): 513-518.
40. Cho, Uichung, KL Wood, RH Crawford (1998) "Online functional testing with rapid prototypes: a novel empirical similarity method." Rapid Prototyping Journal 4(3): 128-138.
41. ASME Boiler, Pressure Vessel Committee (2010)“ASME boiler and pressure vessel code. Section II, Part D: Properties (Metric) materials”. American Society of Mechanical Engineers.
42. Yanzhen Liu (2013)"Optimize truss beam in the large column by the relative stiffness similar criterion." M.S. Thesis, Tianjin University.