Overview on Model Parameter Identification Problems: Application to Modal Identification and Damage Detection Using Wavelet Transform Volume 1 - Issue 5

Pierre Argoul¹ and Michalis Fragiadakis²*

• ¹Head, EMGCU/MAST Laboratory, Univ. Gustave Eiffel, France
• ²Associate Professor, National Technical University of Athens, Greece

Received: June 16, 2021   Published: July 29, 2021

Corresponding author: Michalis Fragiadakis, Associate Professor, School of Civil Engineering, National Technical University of Athens, Greece

 

Abstract PDF

Abstract

The paper discusses the use of wavelet transform for modal identification and damage detection. The aim is to solve an inverse problem for damage detection of engineering structures using wavelet analysis. Wavelet transform is discussed within the framework of inverse problems; critical aspects and implementation issues for modal identification and damage detection are provided. A dynamic test on a masonry wall and a short example of an eight-storey steel frame building are presented to demonstrate the potential of the approach.

Keywords: Inverse Problems; Ill-Posed Problems; Wavelet Transform; Modal Identification; Damage Detection.

Introduction

Physics was built through the development of theories, that is, by solving direct problems where one goes from a model to the corresponding measurable data. The passage of the data to the parameters of the model - the resolution of a so-called “inverse” problem - is an inverse process as opposed to the natural approach of physics. The term “inverse problem” appeared in the 1960s, notably to designate in geophysics the determination, through input-output or cause-effect experiments, of unknowns in the physics equations. In France, the 1980s witnessed A. Tarantola, one of the precursors of inverse problem theory. He resolved inverse problems concerning the processing of geophysical data principally by means of probabilistic models, i.e the Bayesian approach. Tarantula is the author of several books [1,2] and of numerous articles[3] on the subject.

The goal of this work is to present the tools necessary for modal identification and damage detection from measurements of structural response. Wavelet transform is adopted to estimate the modal parameters of the structural system and detect damage. It is shown that the application of wavelet transform methods is challenging, especially in the case of transient, nonstationary, loading that does not constantly excite the primary modes of the system.

Inverse Problems

There are two kinds of inverse problems. Inverse problems either designate the best possible reconstruction of missing information to estimate the loads (source or cause reconstruction problem), or they are used to determine the values of structural parameters (parameter identification problem) [4]. The paper will focus on the latter point, where the inverse problem arises from the confrontation of experimental data with results from numerical simulations. Despite its great practical importance, the theory of inverse problems remains poorly understood. One characteristic of inverse problems is being ill-posed, or incorrectly posed, in the sense of Hadamard [5]: “the total measured data does not allow the existence of a solution to the problem, the solution is not unique, or, even further, due to disturbance in the data the solution is not stable”. Furthermore, since for an underdetermined problem there are often several possible solutions, it is necessary to specify the confidence level that one can give to each solution. For these problems, the data can also be affected by a likelihood coefficient, or they can be probabilistically weighted. A Bayesian approach is often preferred in the latter case. Finally, another definition for an inverse problem could be: “an ill-posed problem that has for its objective the inversion of a physical model by means of a partial image of that model’s effects”.

The data from measurements can, in theory, create a space of either finite or infinite dimensions, while in practice they are always finite and discrete. When the number of parameters in a model is smaller than the number of measurement data points, then the problem is called overdetermined. In this case, it may be possible to add a criterion that reduces or eliminates the effects of aberrant data. On the other hand, if the problem consists in determining continuous parameters that are thus sampled from a very large number of values, and if the number of results from the experiments is insufficient, the problem is called underdetermined. It is then necessary to use a priori information to achieve a reduced number of possible solutions, or, in the best case, only one.

The range of inverse problems is broad, involving diverse issues, a host of applications, and obviously a wide variety of methods. In 2008, a collective publication [6] aimed to create an inventory of the various inverse techniques in Mechanical and Civil Engineering, developed in the Ministry of the Environment, Energy, Sustainable Development and Territorial Planning of France. Many different inverse problems were considered: identification of mechanical parameters for a compressor, of modal parameters or of a discrete hysteretic system, identification of causes, detection and recognition of images, optimization of noise barrier walls, characterization of heterogeneities as well as various tomographic problems applied to geophysics and the close examination of art works. The numerical resolution methods proposed here range from, the now classic, optimization methods in regular or convex cases to metaheuristic methods of global optimization, for which a CD with a toolbox in Scilab was included.

Regularization Of Ill-Posed Problems

The solution obtained by regularized inversion will depend upon the data in a continuous manner, and will approach the exact solution, supposing that it exists. The regularization of an inverse problem consists of rewriting the problem and is based on two guiding principles:

a) Define a framework for considering a priori supplementary information “exterior to mathematics.”

b) Assure that the new solution is stable and will consider additional information from measurement errors

c) Several methods exist to regularize an inverse problem. These methods can be used alone, or they can be combined. Some examples are

d) Tikhonov’s regularization (the most well-known method, cf. [7,8], which works by adding a non-negative stabilizing functional into the functional to be minimized. The stabilizing functional can take the smallest possible positive values and to consider the available prior information

e) Reduction of the number of parameters, to diminish the sensitivity of the criteria to data fluctuations

f) Introduction of constraints (equalities or inequalities confirmed by the unknowns) into the functional to be minimized, to obtain physically acceptable values

g) Filtering of measurements data through techniques of signal processing (frequency filters, modified Fourier transforms, time frequency transforms, etc. [9]). Time frequency transforms, such as wavelet analysis (cf. [10, 11, 12, 13]), can be particularly suited to analyze data that change over time

h) The method of quasireversibility, initially proposed by R. Lattès and J.L. Lions [14]. This method is well-suited for Cauchy problems, such as in elliptic partial differential equations [15]. It consists of modifying the differential or partial differential operator, generally by changing the order of the derivatives that it operates on. This is performed in such a way as to obtain a new problem that is well posed for the initial data, or for the known boundaries.

Optimisation Problems

As above mentioned, an inverse problem most often boils down to a problem of minimizing the difference between calculation and experimental results, or to a problem of maximizing likelihood. The inverse problem thus leads to an optimization problem, which is often a large problem in and of itself.

The numerical techniques used to solve an optimization problem are as varied as the domains to which inverse problems themselves can be applied. Some notable examples are: linear or non-linear least squares, maximum likelihood, Monte-Carlo method, linear programming, simulated annealing, genetic or evolutionary algorithms, optimal control methods, etc. Since a detailed list of optimization methods is beyond the scope of this work, the reader can consult the vast literature on this subject, from which we mention the books of Fletcher [16] and that of Trélat [17] on control theory, the objective of which is either to stabilize the system to make it insensitive to certain disturbances (stabilization), or to determine optimal solutions for a certain optimization criterion (optimal control). The work of Culioli [18] is simple and presents the most common numerical methods, that of [19] concerns both optimization and control, while the work of Groetsch [5] is more oriented towards inverse problems. For deterministic methods and convex problems, one might consult [20], and for non-deterministic methods and discrete optimization, reference [21] is a very useful work.

Modal Analysis - Modal Identification

Modal identification is an important part of structural health monitoring and damage detection. It can also be qualified as “inverse vibrations”, following the words of H.D. Bui [22]: “How, from a vibrations test on the studied structure, to know the characteristics of the model of its mechanical behavior?”. The aim is to use only the output signals to estimate structural properties such as natural frequencies, mode shapes, energy dissipation characteristics, and strength or stiffness deterioration, mainly in the low frequency range. These structural parameter estimations can be found via the system dynamic responses in the low-frequency range [23]. Modal identification essentially requires an inverse problem to be solved from recorded measurements. It can be performed either in the time, the frequency, or more recently, in the time-frequency domain. Several approaches to perform time-domain system identification have been developed, such as state estimation using Kalman filter, stochastic analysis and modeling, recursive modeling, and least squares method. System identification and fault detection techniques have also been proposed. Modal identification methods based on the use of both input (excitation) and output (response) measurements to estimate the modal parameters are called inputoutput dynamic identification techniques. They belong to the field of traditional Experimental Modal Analysis (EMA) [24, 25, 26]. Methods in the time and frequency domain can be further divided into indirect methods (modal methods) and direct methods. The term “indirect” means that the identification is based on the modal model, i.e., on the modal parameters (natural frequencies, modal damping ratios, modal shapes amplitude and their phase). The direct method refers to the identification procedure related to the spatial model, i.e., the equilibrium matrix equation from which all the methods are deduced.

An overview of the modal input-output identification methods is presented in Figure 1. The classification follows the work of Maia et al. [24], while a new column has been added to include the timefrequency domain and the associated techniques using wavelet analysis on measured response signals of linear mechanical systems under vibration. These techniques appeared from the 1990s and were first applied to transient responses of structures to identify their modal characteristics [10]. Since the 1960s, EMA has obtained substantial progress and numerous modal identification algorithms have been developed, from single-input/single-output techniques to single-input/multi-output and MIMO techniques, either in the time domain (TD), or in the frequency domain (FD). The goal of these identification methods is to extract from measurements of structural excitation as much modal information as possible.

To predict the dynamic properties of a mechanical system, it is necessary to formulate a mathematical model, as accurately as possible, in terms of structural parameters such as the mass, the stiffness, and the damping matrices. However, since most mechanical systems are complicated, it is difficult to accurately estimate these system parameters. As a result, many studies use theoretical and experimental methods to identify the structural parameters. It must be mentioned that the type of mathematical model, e.g., based on beam elements, 2D FEM, ect should be compatible, to the extent possible, with the quantities that will be measured.

For large-scale structures, the controlled input force generation is often difficult to achieve. Thus, a set of new modal identification methods which do not require controlled input, known as “outputonly modal identification techniques” has significantly developed in recent years. These methods work satisfactorily if some, general, conditions are met. These conditions are not overly restrictive and concern the stochasticity of the input. Every year, hundreds of papers that cover a wide range of applications related to the extraction of modal properties from measurement data appear in more than two dozen mechanical, aerospace, and civil engineering journals.

For example, the method of measured frequency response functions (FRFs) can be directly used to identify the modal parameters. However, the noise effect and the matrix inverse operations create ill-posed problems since a small noise level may contaminate the identification process, as, for example, in the case of structures with bolted joints [27].

Conventional modal analysis techniques have been proven to be efficient for extracting accurate modal parameters. However, when two modes of interest are moderately close, conventional modal analysis becomes inapplicable. When damping is light and the different modal frequencies are well-separated, which is often the case in many practical situations, the assumption of “proportional damping” in which the normal modes are real and the modal damping matrix is diagonal is justified, since the influence of the off-diagonal terms is negligible. In the case of non-proportional viscous damping, a time-frequency identification technique based on wavelet transform was formulated by Erlicher and Argoul [12] and was applied to free-decay responses of linear systems. The Cauchy mother wavelet is used, while frequencies, modal damping ratios and complex mode shapes were identified from output-only free vibration signals. This identification technique has also shown to be effective when the (non-proportional) damping is significant.

Wavelet Transforms

Since its first definition in the beginning of the 1980s by French researchers, especially Grossmann and Morlet [28], the growth of wavelet research in mathematics has been first explosive with significant contributions from numerous authors. Its successful application in signal and image processing rapidly increased soon after the appearance of the method. Although wavelet analysis is becoming more and more frequently used in engineering applications, it is still far from being systematically used in civil engineering, certainly due to the insufficient knowledge of the properties of the wavelet transform. Continuous wavelets transform (CWT) is a powerful tool for identification of modal properties, but it is difficult to obtain an accurate estimation of the time instants that the structural properties are modified. The basic idea of the CWT is to use a function ψ(t) called the “mother wavelet”, which can generate a basis ψa,b(t) = (1/a)ψ[(t-b)/a] for the time-frequency domain of a function x(t). Using a mother wavelet, CWT can be used to decompose a function x(t) into the frequency-time domain as follows:

where ψ* is the conjugate of ψ. The factor 1/guarantees that the wavelet maintains constant energy. The L2 norm of Wa,b(t) is appropriate when the modulus-squared wavelet transform is desired to reflect the energy of the analyzed signal. However, it is generally more useful to describe time-localized signals by their amplitude, and for this the 1/a normalization (L1 norm) is more appropriate.

For the successful CWT decomposition, it is essential to control the time-frequency resolution of the wavelet transform of the signal. This is necessary to correctly interpret its CWT plot and to consider edge effects [10]. Referring to the conventional frequency analysis of constant-Q filters, Le and Argoul [10] introduced a parameter Qm called “quality factor” for the time-frequency resolution of the CWT. This Qm factor is defined as the ratio of the mean value f* (For L2 norm) over to two times its standard deviation Δf, i.e., it can be calculated with the aid of the expression:

Another important aspect is the extraction of ridges. The possibility of the extraction of ridges for two close eigen angular frequencies ωi and ωj, is guaranteed if the following condition is satisfied:

where cf is a constant given in reference [9], λi is the modal damping ratio of the ith mode and i and j are indexes of two neighboring modes. If the condition above is not met, the extraction of accurate ridges is not guaranteed since there are modes that are too close, and they cannot be separated if they are damped too much. If this condition is met, it does guarantee the extraction of accurate ridges, this is guaranteed by the quality factor Qm [10].

When the ridges are known, the modal shapes can be estimated through the wavelet transform of output response at point k and a reference point, e.g., the top of a building. The i-th mode, φi, is calculated as:

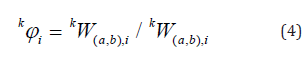
Examples

The first example focuses on vibration data that were acquired during an experimental campaign carried out on masonry wall specimens. These data were used to apply the technique described in references [29, 30] for the dynamic identification through transient responses embedded into noise responses.

The experimental campaign was carried out on UnReinforced Masonry (URM) panels subjected to Shear-Compression (SC) and ambient-vibrations tests through a system of accelerometers (Figure 2). Observing the acquired data, some of them were unusual signals as an outcome of ambient vibration excitation. In fact, they contain some discontinuities in the waveform that can be assumed as transient responses, i.e., change in the steady state of the system. These responses are probably due to the testing environment triggered by other testing machines. The implementation of CWT analysis applied to selected transient signals allows to detect spurious modes created by noise or redundant degrees of freedom of the model and to identify the presence of close modes and the related modal parameters.

Carpine et al. [30] presented an adapted modal identification method based on wavelet analysis that has been proven to be promising for the processing of free responses of nonproportionally damped systems, integrated in noise, to directly obtain complex modes. A procedure for choosing an appropriate quality factor for the time-frequency resolution, necessary to get correct identification results in the case of free responses combined with responses to ambient excitation and/or to additive noise, is detailed.

For response at each measurement point uk, a ridge ak can be extracted from the time-frequency plot, for all the modes excited by the shock [10]. A new procedure in [30] is proposed to extract a single ridge aΣ instead of several ridges ak (one for each measurement point), defined for N measurement points uk using the following formula:

The effect of the quality factor is illustrated in Figure 3 where the absolute value of is plotted. The optimal choice of Q is discussed in reference [30] to facilitate the ridge extraction and better estimate the modal parameters. This is particularly important when two Eigen frequencies are close and difficult to separate.

The second example is an eight-storey steel frame subjected to the El-Centro earthquake. Figure 4 shows the frame, the vertical loading according to the seismic load combination and the section properties. The seismic response assessment of such structures is discussed in detail in Fragiadakis et al. [32, 33]. The scalogram of the velocity of the top storey is shown in Figure 5a. It is shown that not all the modes of the structure are triggered during the seismic loading, while multiple modes are affected during the time history.

Taking a section, parallel to the frequency axis at the time when the scalogram reaches its maximum value, reveals some of the Eigen frequencies of the response. Therefore, a section at t*=12sec, allows to identify the structural modes from the peaks or the ridges (Figure 5b). Peaks that are in neighboring frequencies practically will correspond to the same mode, although this is not the case here. The modal shapes obtained are shown in Figure 5c. The modes were obtained after repeating the wavelet transform on the response signal of each story and then applying Eq. 4. If a section, like that shown in Figure 5b is taken for every signal, the first three peaks of the signals correspond to the first three modes which have efficiently identified with the aid of CWT as shown in Figure 5c. Damage identification can be performed through identifying changes of the modal shapes during the seismic loading. For this purpose, more sections parallel to the frequency axis, e.g., Figure 5b, can be considered to identify the increase in the Eigen frequencies of the building due to large inelastic displacement and rotation demand. For regular buildings of small-to-medium height the increase will affect primarily the first mode, while the higher modes will, most probably, remain linear elastic [34].

Conclusions

The paper discusses the use of wavelet transform methods for modal and damage identification of structures from their responses (transient or seismic). Two example applications have been presented: a masonry wall subjected to shocks embedded into noise excitations during shear compression tests and an eightstorey steel frame subjected to seismic loading. The two examples show the capacity of wavelet transform methods that can be used to efficiently handle inverse problems and can give valuable information for structural damage assessment.

References

1. Tarantola A, Morlet J (1982) Inverse problems quest for information. J Geophys, 50: 159-170.
2. Tarantola A (1987) Inve rse problem theory – Methods for data fitting and model parameter estimation. Elsevier Science and Technology.
3. Mosegaard K, Tarantola A (1993) Probabilistic approach to inverse problems. chapter International Handbook of Earthquake and Engineering Seismology, pages 237-265.
4. Argoul P (2012) Overview of inverse problems. Master lessons. “Introduction to parameter identification in civil engineering”, Ecole Nationale des Ponts et Chaussées, p.13.
5. Groetsch CW (1993) “Inverse Problems in Mathematical Sciences,” Vieweg Publishing, Wiesbaden,
6. P Argoul, N Point, G Dutilleux (2008) Problèmes inverses en génie civil. Coll. Etudes et Recherches des LPC, SI 15 LCPC, Paris, 265 pages + CDrom.
7. Tikhonov AN, Arsenin VY (1977) Solutions to ill-posed problems. Winston-Wiley, New-York.
8. Hanke M, Engl HW, Neubauer A (1996) Regularization of inverse problems. KAP.
9. Carmona R, Hwang WL, Torrésani B (1998) Practical time-frequency analysis. Academic Press, New York.
10. Le TP, Argoul P (2004) Continuous wavelet transform for modal identification using free decay response, Journal of Sound and Vibration 277(1-2): 73-100.
11. Argoul P, Erlicher S (2005) Mechanical modelling and computational issues in civil engineering, volume 23 of Lecture Notes in Applied and Computational Mechanics, chapter on the use of continuous wavelet analysis for modal identification, pages 359-368. Springer.
12. Erlicher S, Argoul P (2007) Modal identification of linear non-proportionally damped systems by wavelet transform, Mechanical Systems and Signal Processing 21(3): 1386-1421.
13. Rouby C, Pecol P, Rémond D, Argoul P (2009) Wavelets or Chebyshev polynomials continuous-time identification of mechanical systems, IFAC Proceedings Volumes, 42(10): 1346-1351.
14. Lattès R, Lions JL (1993) Méthode de quasi réversibilité et applications. Eds Eyrolles.
15. Bourgeois L (2007) A stability estimates for ill-posed elliptic Cauchy problems in a domain with corners. CR Acad Sci Paris, Ser I, 345(7): 385-390.
16. Practical methods of optimization. JohnWiley and Sons, 1980.
17. Trélat E (2008) Contrôle optimal: théorie et applications, 2nd edition, Vuibert, Collection “Mathématiques Concrètes”, 250 pages.
18. Culioli JC (1994) Introduction à l’optimisation. Ellipses.
19. Boyd S, Vandenberghe L (2004) Convex Optimization. Cambridge: Cambridge University Press.
20. Horst R and Pardalos PM, (1995) editors. Handbook of global optimization. Kluwer Academic Publishers.
21. Pardalos PM and Romeijn HE (2002) editors. Handbook of global optimization - Nonconvex optimization and its applications), volume 2. Springer, 1 Ed. 6.
22. Bui HD (1993) “Introduction aux problèmes inverses en mécanique des maté” Collection de la Direction des Etudes et Recherches d’Electricité de France. Eds Eyrolles.
23. Argoul P (2004) Quelques réflexions sur l’identification de paramètres en dynamique des matériaux et des structures. Hdr (In French), Claude Bernard University, Lyon 1, pp.144.
24. Maia et al., (1997) Theoretical and Experimental Modal Analysis, Research studies Pre Edts, pp. 468.
25. Ewins DJ (2000) Modal testing, 2nd edn. Research Studies Press, Baldock.
26. Cunha Á, Caetano E (2006) “Experimental Modal Analysis of Civil Engineering Structures”, Sound & Vibration, 40(6).
27. Li L, Cai A, Guo T et al. (2014) Solution of ill-posed problems for identification of the dynamic parameters of bolted joints, J Mech Sci Technol 28: 3471-3481.
28. Grossmann A, Morlet J (1984) Decomposition of hardy functions into square integrable wavelets of constant shape, SIAM, Journal on Mathematical Analysis 15 (4): 723-736.
29. Ientile S (2017) Sensitivity and dynamic identification of damaged unreinforced masonry walls, PhD Thesis, IUAV University of Venice, Venice, Italy.
30. Carpine R, Ientile S, Vacca N, Boscato G, Rospars C, et.al. (2021) “Modal identification in the case of complex modes – Use of the wavelet analysis applied to the after-shock responses of a masonry wall during shear compression tests”, Mechanical Systems and Signal Processing, 160: 107753.
31. Fragiadakis M (2014) “Response spectrum analysis of structures subjected to seismic actions”, in Encyclopedia in Earthquake Engineering, Beer, M, Kougioumtzoglou, IA., Patelli, E, Au, ISK, (Eds.), Springer-Verlag, Berlin.
32. Fragiadakis M, Vamvatsikos D, Karlaftis M, Lagaros N, Papadrakakis M et.al. (2015) “Seismic assessment of structures and lifelines”, Journal of Sound and Vibration, 334: 29-56.
33. Fragiadakis M, Vamvatsikos D, Aschheim M (2014) “Application of Nonlinear Static Procedures for Seismic Assessment of Regular RC Moment Frame Buildings”, Earthquake Spectra, 30(2): 767-794.