Modeling and Performance of an Integrated Solar Water Pumping System Volume 1 - Issue 3

Said MA Ibrahim¹*, Hamdy H El-Ghetany² and Ahmed GM Shabak¹

• ¹Mechanical Engineering Department, Faculty of Engineering, Al-Azhar University, Cairo, Egypt
• ²Solar Energy Department, National Research Centre, Dokki, 12622, Giza, Egypt

Received: February 07,2021   Published: February 26, 2021

Corresponding author: Said MA Ibrahim,Mechanical Engineering Department, Faculty of Engineering, Al-Azhar University, Cairo, Egypt

DOI: 10.32474/JOMME.2021.01.000117

 

Abstract PDF

Abstract

Solar water pumping systems provide a proper energy solution especially in rural and isolated areas where the traditional sources of power (electricity or diesel) are unavailable or very costly. Solar energy is available with abundant quantities of daily irradiance, and it is a clean and carbon free source of energy. The present work furnishes a mathematical model and performance evaluation of an integrated solar water pumping system for different water demands through a comprehensive design tool simulation program prepared and designed by the authors. The model calculates the solar radiation data for the selected cite. The simulated model, based upon the solar radiation values, can provide, for the specified water demands, the related hydraulic pump electric power for the desired pump total dynamic head, the required PV peak power and its related area requirements, and the corresponding total cost of the system components in Euro. The present program is universal and can be used to design solar water pumping systems anywhere in the word. The present results are for Cairo Egypt, for water demands range from 50-300 m3/ day. Egypt enjoys an average value of solar radiation of 5.5 kWh/m2/day. The present research offers a good accurate quick tool for designers, users, and buyers of such systems.

Keywords: Mathematical model; Solar; Water pumping system; Water demand; Efficiency; PV sizing; Cost

Introduction

To narrow the present gap between water demands and the required energy needs in the agriculture sector in Egypt as in many countries, Solar Water Pumping Systems (SWPS) are considered essential priority solution to provide the required energy for these demands. A SWPS can be a cost effective, stand-alone for serving the remote water needs, whether it is for irrigation, animal grazing, or potable use. The present research is applied to Cairo, Egypt. The need of solar pumps in Egypt is an extremely important topic that depends on the availability of solar radiation and the amount of stored underground water. The availability of underground water in the Egyptian desert is given by theNational Specialized Boards [1].Solar radiation is abundantly available since Egypt is lying in the middle of the solar belt countries with an average value of 5.5 kWh/m2/day. Solar energy is renewable and clean source of energy. Being zero carbon source, it can effectively reducehigh pollutions, global warming, and climatic changes. SWPS has low operating costs in general that gives it the advantage of being cost-effective systems. The irrigation water withdrawal is the sum of the actual water needed for irrigation, with the addition of the water that is lost in its distribution and application, which by far exceeds the consumptive use of irrigation [2]. Much research has been carried out to minimize the losses of irrigation water. Drip irrigation is the method that allows for the lowest water losses and consequently needs the least amount of water in order to sufficiently irrigate plants [3]. Most current photovoltaic (PV) pumping systems are equipped with a Maximum Power Point Tracker (MPPT). This electronic device is a DC-DC converter that is able to operate the PV array in its maximum power point for any given solar irradiation [4]. A benefit of using solar energy to power agricultural water pump systems is that the increased water requirements for livestock and irrigation tend to coincide with the seasonal increase of incoming solar energy. This means that the volume of water pumped by the SWPS in a given interval depends on the total amount of solar energy available at that time period. Specifically, the flow rate of the water pumped is determined by both the intensity of the solar energy available and the size of the PV array used to convert the solar energy into direct current (DC) electricity. The principal components of the SWPS are PV array and its supporting structure, an electrical controller, and an electric powered pump [5]. It is important that the components be designed as part of an integrated system to ensure that all the equipment are compatible and that the system operates as intended.Solar-powered pumps are characterized as either positive displacement pumps (e.g., diaphragm, piston, or helical rotor) or centrifugal pumps. Positive displacement pumps are typically used when the Total Dynamic Head (TDH) is high and low flow rate. On the other hand, centrifugal pumps are used for low TDH and high flow rates.
The scope of this research paper is to present a mathematical model and build a simulation program to evaluate the performance of the SWPS for different flow rates and TDH. Finally a complete sizing of the system components is identified and the integrated system cost, power, and land requirements are estimated. The present results are for Cairo, Egypt.

Components of The Solar Water Pumping System

It is essential to calculate the adequate power rating for a photovoltaic system to meet the total required electrical load. Prior to the design of the system, the daily average sun hour, amount of daily solar radiation falling on the horizontal surface, and the ambient temperature should be defined. The SWPS consists of the following components [6].
a) PV module which converts solar energy into electricity to run the pumps.
b) Inverter to covert DC power generated from the PV panel to AC to meet the load of pumps.
c) Battery bank to drive the pumps shortage of solar radiation and charger controller to regulate and adapt battery charging (in case of using storage system).
d) Variable speed pump to be operated according to the variable solar energy input (in case of not use storage system).
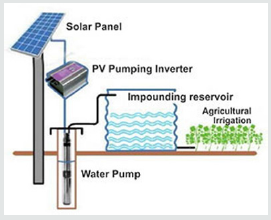
An SWPS as described above with a variable speed pump is illustrated in (Figure 1)

Theoretical Modeling of The Solar Water Pumping System

The proper design of an SWPS, for certain cite and application, requires some basic information which are:
i. The amount of solar energy incident on the horizontal and inclined surfaces.
ii. The required water demand.
iii. The total dynamic head (TDH) of the pump.
iv. Selecting a pump that satisfies both the water demand and the desired pressure.
v. Estimating the PV power to meet the demanded electric load for the chosen pump.
vi. Calculating the area of PV modules required for the system.
vii. Determination of the total SWPS cost of the integrated system.

The Present Computer Simulation Program

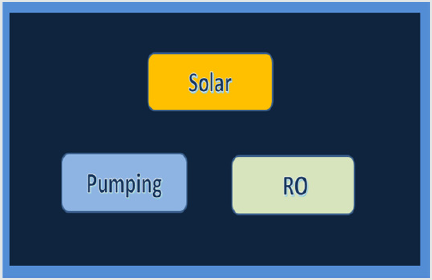
The present software package has three main routines: solar, pumping, and desalination. The program has one main input screen which presents the three main tabs of the program, solar, pumping, and desalination, as illustrated in (Figure 2) In the current work, only solar and pumping categories are used.

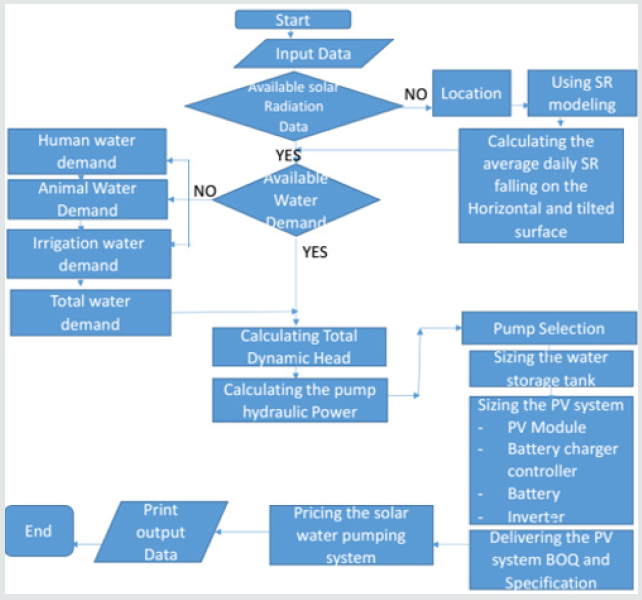
A computer simulation program was specially designed based on the mathematical model of the system components and, according to the algorithm indicated in the flow chart depicted in (Figure 3) This computer program is fed with the necessary input data, and the output lavishes all the required design results for the SWPS. The program is even capable of giving the recommended companies that can supply all the selected equipment of the system. The program is versatile enough such as it can provide different solutions to choose from based on the input data and costumer requirements and available budget. This software tool is difficult to construct, however simple in use. It is a time saver, and can help the designer or customer to study, easily and quickly, different system design cases or proposals and perform several runs without going to redesign again and again for each case. Also, it allows the designer to decide upon the main components of the system, like PV module, inverter, charge controller, and pumps from different manufacturers. The program is versatile and can provide different solutions to choose from based on the input data, costumer requirements, and budget. The present computer program acts as a solar energy recipe.

The present computer program is general in the sense that it can be used anywhere in the world, as long as the appropriate input data are used.

Calculating the Amount of Solar Energy Falling on The HorizontaL

The daily extraterrestrial radiation on a horizontal surface (Ho), at any day of the year, n (n= 1 for January 1 etc.), is calculated by [8]

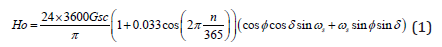
where
Gsc is the solar constant equal to 1,367 W/m2,
δ is the declination angle
s ω
is the sunset hour angle, and
φ is the latitude angle of the site.

The declination angle (δ ) can be given from Cooper’s equation [8]

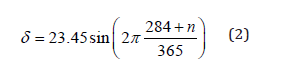
The solar hour angleis equal to zero at solar noon and varies by 15 degrees per hour from solar noon. It takes negative sign in the morning and positive sign in the afternoon.
The sunset hour angle ( ) s ω is an angle equal to the solar hour angle when the sun sets, and is determined from this equation

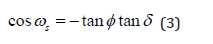
The extraterrestrial radiation on a horizontal surface for an hour period can be estimated by integrating Eq. (1) for a period between hour angles 1 ω and s ω which define an hour (where s ω is the larger) [8]

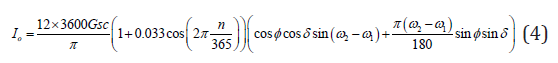
Clearness index: the monthly average clearness index, T K , is the ratio between extraterrestrial radiation and solar radiation at the surface of the earth. Values of, T K depend on the climates condition and the time of year considered. It can be calculated from this equation [8]

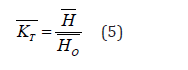
where

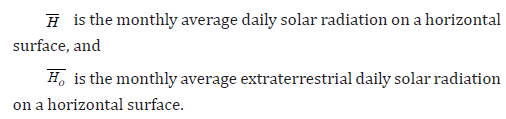
The average radiation on a slope surface can be calculated considering the beam, diffuse, and reflected radiation components by using this equation [8]

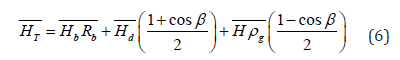
where

Rb = 0 = reflection of radiation on the surface of the earth,

ρ = ground reflectivity, when the monthly average temperature is above 00C = 0.2 and when the monthly average temperature is below -50 C = 0.7 [8], and

β = slope of the collector, and is given by [8]

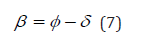
The monthly average daily beam radiation b H , is calculated from this formula

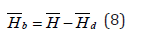
According to sunset hour angle ( ) s ω the monthly average diffuse radiation Hd can be calculated from these equations [8]

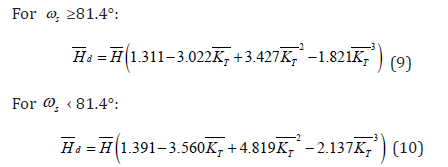
Due to the location of Egypt towards the equator in the northern hemisphere, the ratio between slope surface to the horizontal surface, Rb , is given by [8]

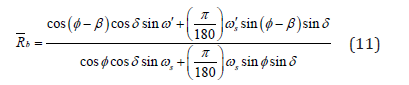
where s ω is the sunset hour angle for tilted surface and is calculated by [8]

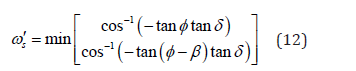
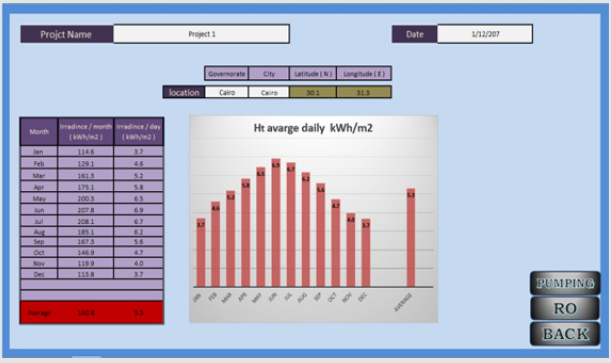
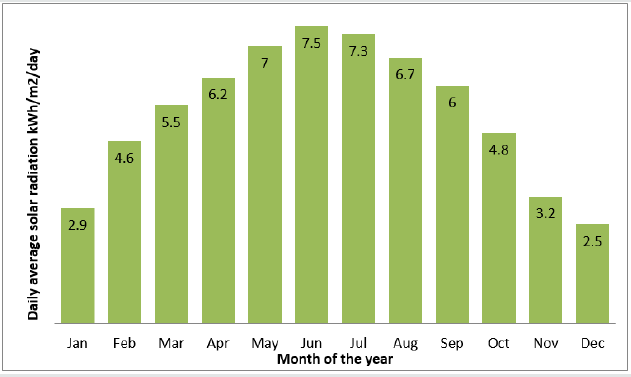
In the following (Figure 4) typical data sheet of the solar radiation data, as obtained from the present simulation computer program, for the given city of Cairo are shown.As seen, the solar radiation detection screen has input and results in the same page. System design variables are inputs in the configuration screen as shown in (Figure 4)

Inputs to the program as depicted in (Figure 4) are:

a) The project name and date are entered in the input boxes.
b) Site location by defining the Governorate, State, County or whatever applicable and the city to obtain the longitude and the latitude of the location.
The input data for Cairo, Egypt, generated the output results indicated in (Figure 4)as:
a) Longitude and latitude of the selected location.
b) Monthly and daily irradiances (kWh/m2).
c) Radiance graph for every month of the year.
This screen is of paramount importance, since all design calculations of the SWPS depend on the accuracy and reliability of the solar radiation results from this software.

Required Water Demand

Calculations of the water demand is based on many different factors like user identity (human, kind of animal, kind of plant), climate conditions for the given site, environment, method of irrigation, lifestyle for humans, and human activities (cooking, drinking, bathing, ...etc). The average total water consumption for different activities is computed based on the Egyptian standard code as [9]

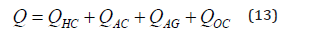
Where

Q_HC = Human water consumption (m³ / day),
Q_AC =Animal water consumption (m³ / day),
Q_AC =Agricultural water consumption (m³ / day) and
Q_OC = Other consumptions (m³ / day).

The daily water demand based on the above given parameters are calculated from the present simulation program, according to the worksheet presented in (Figure 5).

Total Dynamic Head of The Pump

The total dynamic head (TDH) is composed of the total static head (h_s), friction head losses (h_f), and minor head losses (h_m). The total static head is the difference in height between the water source inlet level (h_i) and the water outlet level (h_o). The friction head losses in the system are developed from the wall shear stress created at the interface between the fluid flowing inside the pipes and their walls. These losses are directly proportional to the pipe length (L), and inversely proportional to the inner diameter of the pipe (d). Moreover, friction head losses are related to a friction factor (f), which depends on the Reynolds number (R_e) of the flow and the relative roughness of the inner pipe walls (ε).
Minor head losses (h_m) result from the unstable turbulent flow in pipe fittings, connections, and valves. Its magnitude is quantified by a loss factor (k), which is specific to each type of fitting and independent of the fitting material [10]. The total dynamic pumping head is given as [11]

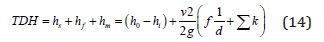
Where
V = Flow velocity (m/s),
I = Pipe length (m),
D = Pipe inside diameter (m), and
K = Loss coefficient for different components
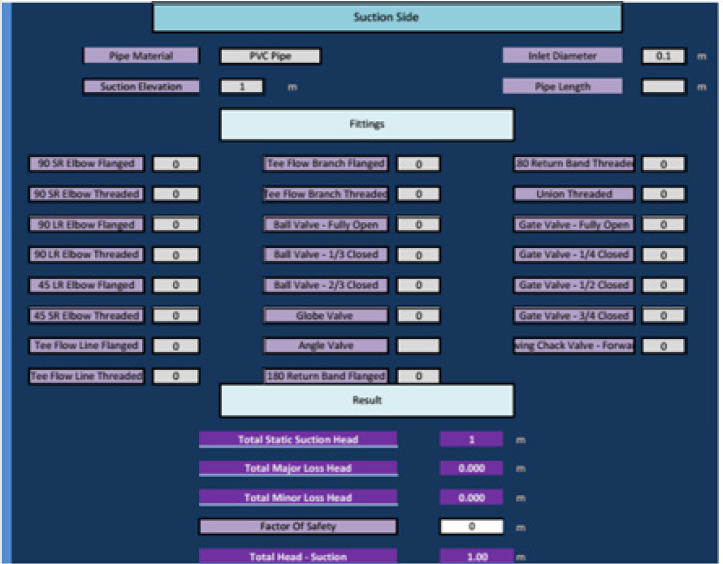
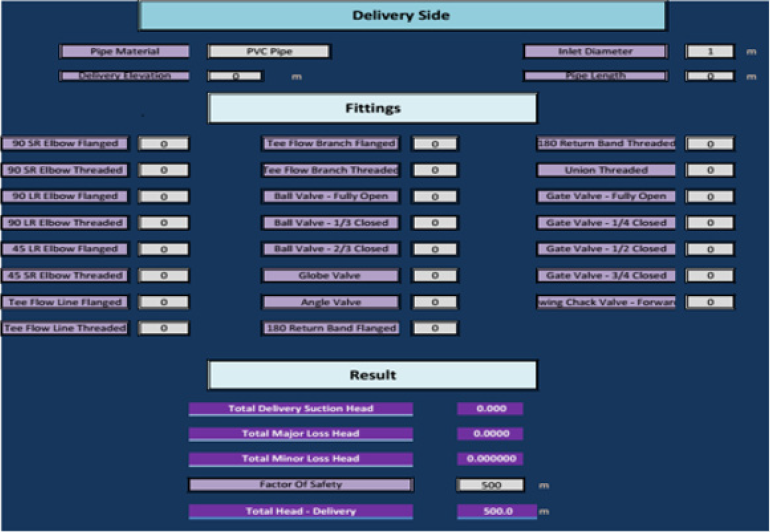
The program output worksheet for calculating the total suction head is exhibited in (Figure 6), and that for the total dynamic head is shown in (Figure 7).

Pump Selection Factors

Pump sizing calculations are based on these factors:
a) Pump flow rate (m3/day).
b) Pumping head (m).
c) Type of pump (centrifugal or positive displacement)
d) Water source (surface or submersible).
e) Different manufacturer’s manuals.

Hydraulic Pump Power

The hydraulic pump power, Ph, required to lift up a certain water volume against a total dynamic head, TDH is given by

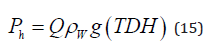
Where
ρ_w = Water density (1000 kg/m³),
g = Acceleration of gravity (9.81 m/s²), and
Q = Flow rate or volume of water lifted, in m³/s.
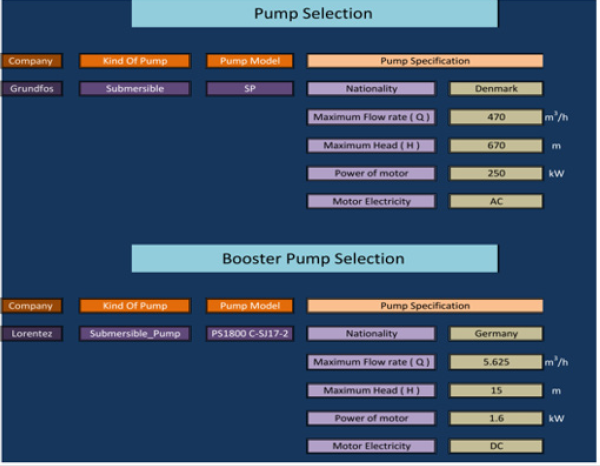
The current computer program allows for a complete selection of surface and submersible pumps as demonstrated in (Figure 8).

Area of The Pv Panels Required for The Integreted Solar Pumping System

The size of the PV system in Wp for the peak load can be defined as [12]

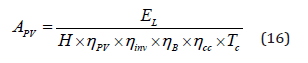
Where
A_pv = Total area of photovoltaic requirement (m²),
E_L = Peak daily required electrical energy for the SWPS (Wh/ day)
H = daily global irradiation (Wh/m²/d),
PV η , inv η , B η , cc η = efficiencies for photovoltaic, inverter, battery and charge controller, respectively, and

T_c = Temperature correction factor of the PV module.

The Pv Power for The System

The required photovoltaic modules power PV P (W), to meet the electrical load demand can be estimated as follows

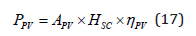
Where
H_sc =Standard solar irradiation, 1,000 W/m². After estimating the total area of PV panels (m²), the number of total modules (N_m) can be determined based on the commercially available area of a single PV panel. The number of modules can be defined as

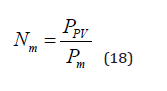
Where
P_m=is the power of the single module (W).
The actual area of all modules, and the exact peak power for all modules , are calculated by

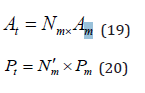
where
A_m is Area of the single module (m2), and N’_m is the corrected number of modules to the nearest integer number.

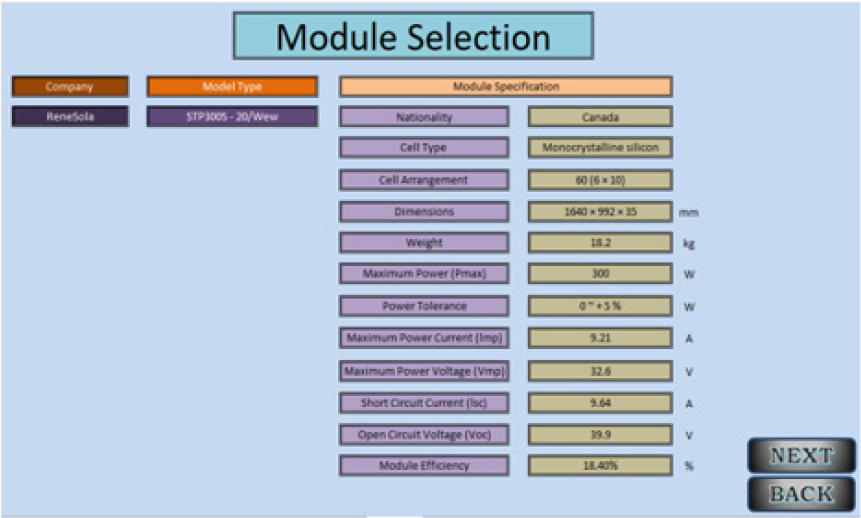
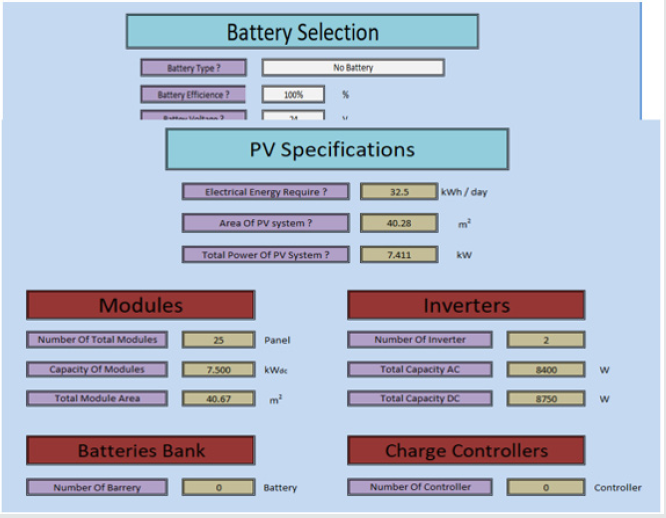
The program will give output data based on the inputs provided for it. The program will lavish data for module selection, invertor selection, battery bank and charge controller, and finally the complete design specifications for the total photovoltaic system to match and necessary to operate the SWPS under consideration. (Figures 9, 10, and 11). exhibit typical output results, for certain given inputs, for module selection, invertor selection, and the final PV system data, respectively.

Cost of The Swps

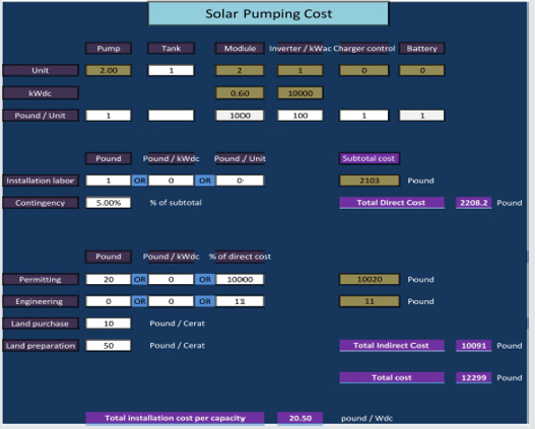
The total cost of the SWPS is determined by our computer program by considering the direct cost, indirect costs, and encountered overheads. The direct cost includes prices of land, buildings if any, and all components of the SWPS such as pumps, PV system, frame structure for the modules, piping, and wiring. The indirect costs and overheads represent land preparation, labor, taxes, levelized costs, and any item whenever applicable. A sample of the computer solar water pumping cost output sheet is illustrated in (Figure 12).

Results and Discussion

Several simulation runs were conducted for the solar water pumping system. The simulated data of the daily average solar radiation for Cairo city is shown in (Figure 13). As the water demand can vary significantly for different water applications (drinking water supply, livestock watering, irrigation, industry, and any application) at different locations in Egypt, therefore six different cases of water needs are used in the simulation model with capacities of 50, 100,150, 200, 250, and 300 (m³ / day).

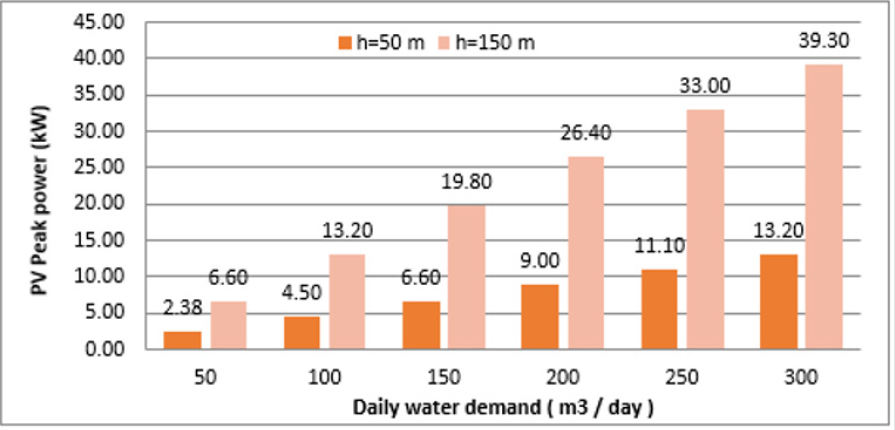
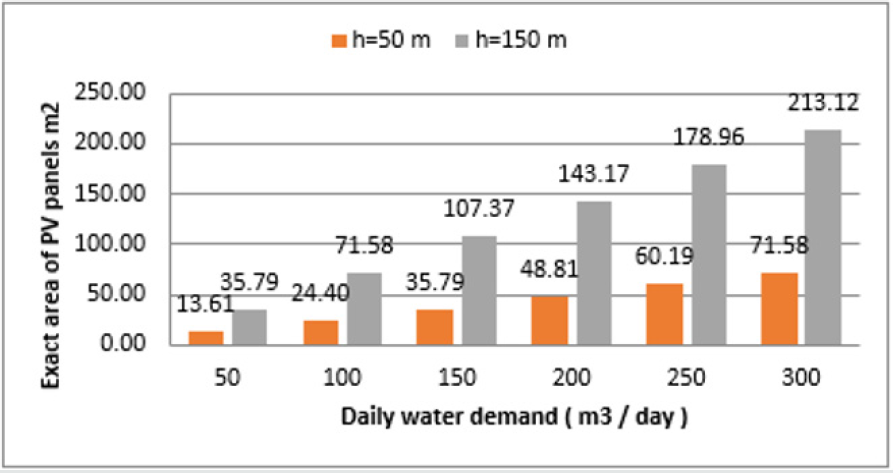
According to the average daily water demand (ranging from 50 - 300 m³/day) and TDH (50 m and 150 m), the power required for pumps in kW can be calculated. The relation between water demands and pump power for different values for TDH (m) is demonstrated in (Figure 14). The SWPS features are calculated based on the electrical power needs with specified water demands as given by Eqs. [17] and [13]. Variations of PV peak power and their related areas with the daily water demands are given in (Figures 15 and 16). The results in (Figures 14-16)are in compliance with the theoretical model equations given above.

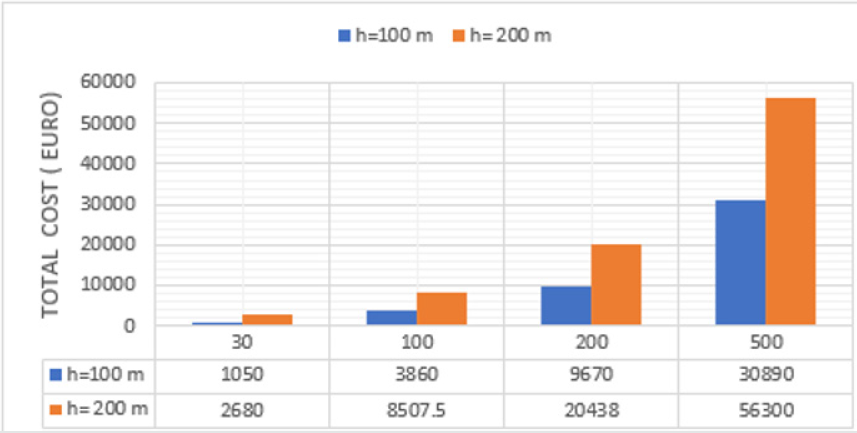
Asa case study for Cairo city several runs of the computer program were performed to get the total cost of the solar water pumping system in Euro for different water demands (m3/day)and different TDH. The obtained results are presented in (Figure 17). It is indicated that the system cost increases as the pump head and water demand increase.

Conclusions

Solar water pumping systems are found to be a good feasible solution for use in many locations and in particular in rural and isolated remote areas where conventional power sources are unavailable, or available at unaffordable cost. In addition, solar energy is a clean source, and abundantly available with an average daily radiation of about 5.5 kWh/m2/day. The present study offers a detailed mathematical modeling and performance evaluation for a complete design of an integrated SWPS, including the PV solar system components for different water demands. This is done by means of a computer program developed and designed by the authors. The program calculates accurately and quickly the pump hydraulic power, PV peak power, PV required area, and total system costs for different pump total dynamic heads and different water demands. The model was applied successfully to calculate for the city of Cairo, Egypt the solar radiation data, and design parameters for the different components of the SWPS, for water demands ranging from 50-300 m3/day. The obtained results comply with the mathematical model. This gives confidence in the present model and software program. The calculated results can be obtained for any water demand, the pump electric power at the desired total dynamic head, the required PV peak power and its related area requirements, and the corresponding total cost of the integrated system in Euro. This program, based on its scientific and commercial merit, offers a much needed powerful accurate good tool for designers, users, and customers. The program is versatile and as such furnishes several solutions for the costumer to select from according to the available budget and desires. The present computer program is quite difficult to construct, but easy to use. It also a time saver. The program is universal and can be applied to any location in the world as long as the proper solar data are supplied together with water needs, and other specific data relevant to the site and project specifications and requirements.

Nomenclatures

A_m Module area, m²

A_t Total area of all modules, m²

Q_AC Daily Animal Consumption, (m³ / day)

Q_AGC Daily Agriculture Consumption, (m³ / day)

Q_HC Daily Human Consumption, (m³ / day)

D Pipe diameter, m

E_L daily required electrical energy for pumps the Wh/d

f Friction factor

g Earth gravity, 9.8 m/^s2

H Daily irradiation ,Wh/m²/d

H_sc Standard solar irradiation, 1,000 W/m²

h_f Major loss, m

h_m Minor loss, m

h_s Total static head, m

k The loss coefficient for different component.

l Pipe length, m

N_m Number of total modules

P_h The hydraulic Power, W

P_PV PV power, W

P_m Module power, W

P_m Module power, W

P_t Total power of all modules, W

Q Total water demand per day, m³/day

TDH Total Dynamic Head, m

T_c Temperature correction factor of the PV module

V Velocity of flow, m/s

h_i , h_o Height difference between water source inlet (h_i) and level of water outlet(h_o),m

ρ Water density, kg/cm³

η_B Battery efficiency

η_C Charge controller efficiency

η_inv Inverter efficiency

η_m Motor efficiency

η_p Pump efficiency

η_pv PV efficiency

References

1. Hatem MA (1990) National specialized board reports, residential Council. The Arab Republic of Egypt 1: 1974-1989.
2. FAO (2015) Aqua stat Database. FAO.
3. Darouich HM, Pedras CMG, Gonçalves JM, Pereira LS(2014) Drip vs surface irrigation: A comparison focusing on water saving and economic returns using multi-criteria analysis applied to cotton. Bio systems Engineering 122: 74-90.
4. Mohammedi A, Mezzai N, Rekioua D, Rekioua T (2014) Impact of shadow on the performances of a domestic photovoltaic pumping system incorporating an MPPT control: A case study in Bejaia, North Algeria. Energy Conversion and Management 84: 20-29.
5. Abdalla M Kishta (2002) "Designing, modeling, and testing a solar water pump for developing countries”. Retrospective Thesis and Dissertations. State University. Paper 391.
6. Kleissl J, Deep-Well, Low-Flow Photovoltaic Water Pumping System Design.
7. Nicholle Kovach (2010) Design of Small Photovoltaic (PV) Solar-Powered Water Pump Systems, Technical Note No. 28, PORTLAND, OREGON, United state department of Agriculture, Natural Resources Conservation Service.
8. Duffie JA, Beckman WA(1991) Solar Engineering of Thermal Processes. 2^nd Edition, John Wiley & Sons, USA.
9. Hamidat A Benyoucef B, Hartani T (2003) Small-scale irrigation with photovoltaic water pumping system in Sahara regions, Renewable Energy 28(7): 1081–1096.
10. Glasnovic Z and Margeta J (2007) A model for optimal sizing of photovoltaic irrigation water pumping systems. Sol Energy 81(7): 904–916.
11. Kudela H (2015) Hydraulic Losses in Pipes, Wroclaw Univ. Sci Technol.
12. Ahmad GE (2002) Photovoltaic-powered rural zone family house in Egypt. Renewable Energy 26(3): 379–390.