Computational modelling of plate-fin and tube heat exchanger for heat transfer and pressure drop analysis Volume 1 - Issue 3

Solomon Mesfin¹², L Syam Sundar²* and Antonio CM Sousa²

• ¹Department of Mechanical Engineering, University of Gondar, Gondar, Ethiopia
• ²Centre for Mechanical Technology and Automation (TEMA–UA), Department of Mechanical Engineering, University of Aveiro, Portugal

Received: October 02, 2020   Published: October 19, 2020

Corresponding author: L Syam Sundar, Centre for Mechanical Technology and Automation (TEMA–UA), Department of Mechanical Engineering, University of Aveiro, Portugal

DOI: 10.32474/JOMME.2020.01.000113

Abstract PDF

The heat transfer and pressure drop characteristics of plate-fin and tube heat exchanger is analyzed by using computational modeling. The parameters which are considered in this analysis are space between the two fins, length of the fin and tube ellipticity. The governing equations of continuity, momentum and energy are solved using the commercially available FLUENT software. Seven different cases are considered for heat transfer and pressure drop analysis. The main findings are related to the spacing between the fins, which is critical in terms of pressure drop. The tube ellipticity provides an increase in heat transfer coefficient and reduces in pressure drop.

Keywords: plate-fin and tube exchanger; numerical analysis; tube ellipticity; pressure drop.

The plate-fin and tube heat exchanger are a cross-flow type heat exchanger, which uses plates as fins as indicated in (Figure 1); therefore, the flow external to the tubes is unmixed. Often, it is categorized as a compact heat exchanger to emphasize its relatively high heat transfer surface area to volume ratio. The plate fin and tube heat exchanger is widely used in many industries, including the aerospace industry, for its compactness and low weight. Different types of fin patterns, in addition to the plate, exist, such as louver, convex-louver, and wavy; however, in general, the plate fin tends to be the best in terms of performance and of constructional effectiveness. The tube geometry used in plate fin and tube heat exchangers is either circular or elliptical. The majority of the studies dealing with plate fin and tube heat exchangers have been conducted resorting to experiments.
Shepherd [1] analyzed early experimental data for heat transfer of plate fin and circular tube heat exchanger. Later on, Schulemberg [2] extended the analysis to plate fin and elliptical tubes. Kayansayan [3] investigated experimentally the effects of the outer surface geometry on the performance of flat plain fin and circular tube heat exchangers with four-row coils. Jang et al. [4] studied fluid flow and heat transfer over a multi row (1–6 rows) plate-fin and tube heat exchanger both numerically and experimentally. They considered effects of different geometrical parameters such as tube arrangement, tube row numbers and fin pitch (8–12 fins per inch) for the Reynolds number (based on the fin spacing and the frontal velocity) ranging from 60 to 900 and observed an average heat transfer coefficient of staggered arrangement is 15%–27% higher than that of in-lined arrangement, while the pressure drop of staggered configuration is 20%–25% higher than that of in-lined configuration. Wang et al. [5] investigated experimentally heat transfer and pressure drop for plate fin and tube heat exchanger. Beecher et al. [6] reported heat transfer data for twenty wavy geometries. Kays et al. [7] analyzed heat transfer and pressure drop of heat exchanger with louvered fins. Achaichia et al. [8] experimentally studied the heat transfer and pressure drop of tube and louvered fin surfaces; later on the same authors [9] conducted a numerical study for flow in the laminar regime. Webb et al. [10] performed a flow visualization study of the louvered fin geometry with a flat tube. Sahnoun et al. [11] developed an analytical model for predicting air-side heat exchanger performance of louvered fin geometry. Rocha et al. [12] experimentally estimated the overall heat transfer coefficient of plate fin heat exchangers by considering circular and elliptical tubes. Kundu et al. [13] conducted a dimensional optimization for plate fin and tube heat exchangers with equilateral staggered triangular and rectangular pitch. Romero-Mendez et al. [14] used numerical techniques to estimate the effect of spacing between fins on heat transfer and pressure drop for single row fin and tube heat exchanger. Wang et al. [15] experimentally analyzed the effect of tube rows, fin pitch, and tube diameter on heat transfer and pressure drop for plate fin and tube heat exchanger. Wang et al. [16] presented correlations of the Colburn and friction factors for plate fin and tube heat exchangers. Saboya et al. [17] determined the average heat transfer coefficient for plate fin and elliptic tube heat exchangers using the naphthalene sublimation technique. Torikoshi et al. [18] numerically investigated a plain fin and tube heat exchanger. Erek et al. [19] numerically investigated the effect of fin geometry on heat transfer and pressure drop for plate fin and tube heat exchangers, but they used one particular mass flow rate of the flue gas. Abu Madi et al. [20] determined the effect of geometrical parameters of flat and corrugated fins and the results are presented in terms of Colburn and friction factors.
The present work is focused on the numerical investigation estimation of heat flow, pressure drop, and temperature and velocity fields for the plate fin and tube heat exchanger with one row tube configuration; the analysis will be focused on the effect of fin spacing, ellipticity and fin height on the numerically predicted parameters.

Figure 1: Plate-fin and tube heat exchanger.

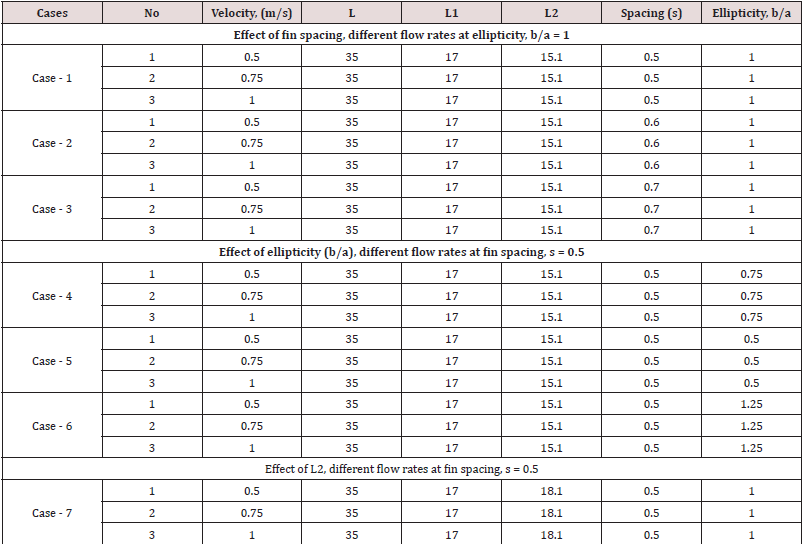
Description of the problem

The plat fin and tube heat exchanger, which is the object of the present study, is schematically depicted in (Figure 2a). The various fin geometries and its dimensions used in this analysis are shown in (Table 1). The computational flue gas flow passage is determined by the spacing of the fins and the distance between the centers of the tube for each consecutive pass. The fins are equidistant and the flow area shown in (Figure 2b,2c) is assumed to be representative of the overall flow passage. The GAMBIT software is used to model the computational domain (Figure 3a), and its meshed view is shown in (Figure 3b). The inlet boundary condition for the flue gas is given by the velocity (0.5, 0.75 and 1.0 m/s) and temperature (1000 K), and the outlet boundary condition is the pressure and no variation of the temperature in the stream wise direction. The flue gas is assumed to have the properties of air. The cooling fluid circulating in the tube is water and it is considered to be fully developed turbulent flow. The convective heat transfer between the tube and fin is calculated using Gnielinski equation [21], which is given as:

Table 1:Different fin cases used in this study.

Figure 2: Schematic representation of fin and tube heat exchanger (b) single fin with tubes arrangement (c) flow area between the fins.

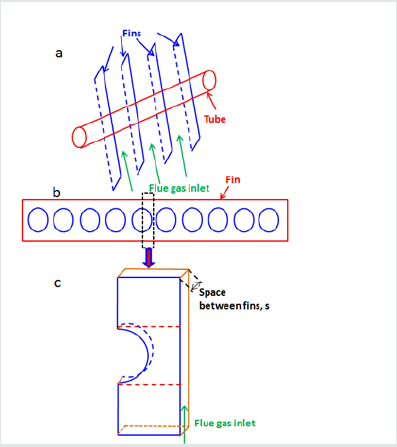
Figure 3(a): Prototype of flow passage between the fins and with dimensions developed in GAMBIT software.

Figure 3(b): Meshed view of the flow passage.

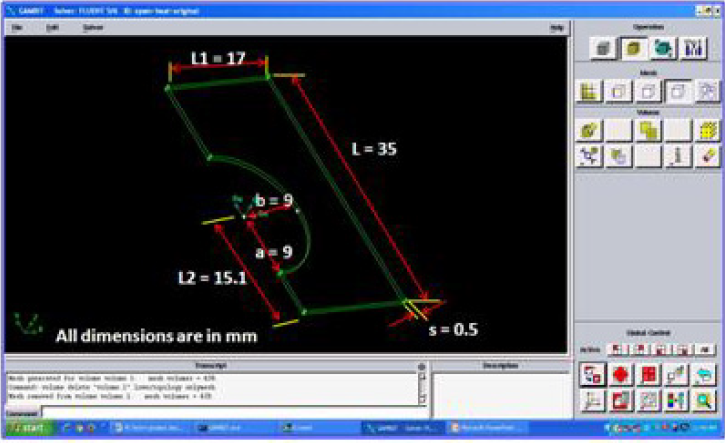
The no-slip boundary condition is applied to the tube and the plate fins. The remaining computational boundaries take a symmetry condition. The material of the tube and plate fins is assumed to be copper.

Governing equations

The process is assumed to steady state and the governing equations describing conservation of mass, momentum and energy are expressed in vector form as follows [22]:
Where, σ_k and σ_ε are the turbulent Prandtl numbers for the turbulent kinetic energy and its dissipation. Turbulent kinetic energy (k) and its dissipation rate (ε) are coupled to the governing equations via the turbulent viscosity relation (μ_t=ρC_μ k^2/ε). C_μ is not a constant value as in the standard k–ε model. The empirical constants, C_2, σ_k and σ_ε are equal to 1.9, 1.0 and 1.3, respectively [24].
The transport equations i.e. Eq. (5) and Eq. (6), after their discretization, are solved sequentially along with the discretized conservation equations. The discretization of the transport equations and conservation equations is conducted using the finite volume method [23] along with a second-order upwind scheme. The continuity equation and momentum equation are solved through an iterative scheme by using the coupling between pressure and velocity is employed through the Semi Implicit Method for Pressure Linked Equations (SIMPLE) algorithm [25]. In this paper, a finite volume based flow solver of computational fluid dynamics software FLUENT 6.0 was employed for the simulation.

Static temperature contours

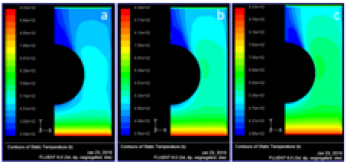
Figure 4: Static temperature contours when the tube ellipticity, a/b = 1 with effect of space between the fins (a) s = 0.5, v = 0.5 m/s (b) s = 0.5, v = 0.75 m/s (c) s = 0.5, v = 1.0 m/s (d) s = 0.6, v = 0.5 m/s (e) s = 0.6, v = 0.75 m/s (f) s = 0.6, v = 1.0 m/s (g) s = 0.7, v = 0.5 m/s (h) s = 0.7, v = 0.75 m/s (i) s = 0.7, v = 1.0 m/s.

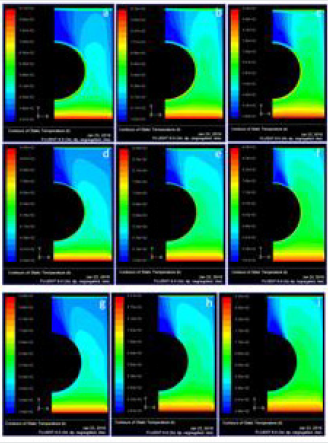
Simulations were conducted for different parameters to determine the static temperature and total pressure fields. Three different velocities of flue gas (0.5 m/s, 0.75 m/s and 1.0 m/s) for all cases studied. The static temperature field for the three velocities for fin spacing, s, equal to 0.5 mm and tube ellipticity, a/b, of 1 is reported in Figure 4 (a-c). As expected, when the velocity of flue gas increases, the outlet temperature of flue gas also increases; the outlet temperatures are 341 K, 362 K and 380 K for inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively. The effect of fin spacing is also analyzed and, to this purpose, three fin spacing are considered: the manufacturer’s standard fin spacing of 0.5 mm, 0.6 mm and 0.7 mm. The static temperature field for each of the three tested flue gas inlet velocities (0.5 m/s, 0.75 m/s and 1.0 m/s) is reported in (Figure 4) (d-f) for a fin spacing, s, 0.6 mm and tube ellipticity, a/b, equal to 1. The outlet temperatures are 343 K, 362 K and 381 K for the inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively; these results are equal or slightly higher than those for the fin spacing of 5 mm, a finding, which is physically consistent, considering the slight reduction in mixing and consequent reduction in turbulence. The static temperature field for the three inlet velocities with a fin spacing, s, of 0.7 mm and tube ellipticity, a/b, equal to 1, presents a similar trend, namely, 346 K, 367 K, and 386 K for the inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively; the results are presented in (Figure 4) (g-i). Therefore, it can be said that an increase in grid spacing will lead to a decrease of the difference between the inlet and outlet temperature.

Figure 5: Static temperature contours when the space between the fins s = 0.5 with effect of ellipicity (a) a/b = 0.75, v = 0.5 m/s (b) a/b = 0.75, v = 0.75 m/s (c) a/b = 0.75, v = 1.0 m/s (d) a/b = 0.5, v = 0.5 m/s (e) a/b = 0.5, v = 0.75 m/s (f) a/b = 0.5, v = 1.0 m/s (g) a/b = 1.25, v = 0.5 m/s (h) a/b = 1.25, v = 0.75 m/s (i) a/b = 1.25, v = 1.0 m/s

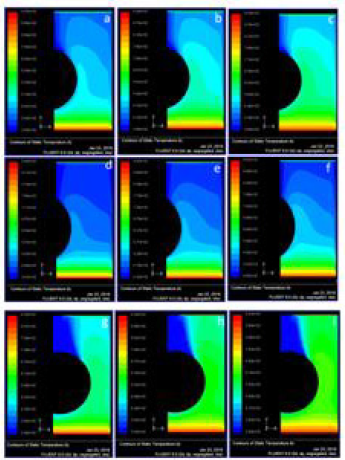
The effect of ellipticity on the temperature field is analyzed for the 0.5 mm fin spacing (s) in what follows. The results reported in Fig. 4 are for the circular tube, which has an ellipticity (a/b) of 1; the other values of tube ellipticity that are considered in this study are 0.75, 0.5 and 1.25, respectively. The static temperature field for the tested inlet velocities (0.5 m/s, 0.75 m/s and 1.0 m/s) with tube ellipticity, a/b, of 0.75 is shown in (Figure 5) (d-f); the flue gas outlet temperatures are 345 K, 365 K and 384 K for the flue gas inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively. For the ellipticity, a/b, of 0.5, the outlet temperatures are 391 K, 425 K and 455 K with the flue gas inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively; while for the ellipticity, a/b, of 1.25, the outlet temperatures are 362 K, 363 K and 363 K with the flue gas inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s, respectively. For the 5 mm fin spacing, the tube ellipticity, a/b, of 1.25 yields the lowest outlet temperature (363 K) for the inlet velocity of 1 m/s, in fact, for this ellipticity, the outlet temperature is practically independent of the inlet velocity in the tested range. The tube ellipticity of 0.5 is the one that leads to the highest outlet temperatures indicating the lowest thermal performance for the heat exchanger.
The influence of the length L2 (Figure 3a) on the temperature field is also analyzed. The change in L2 is equivalent to alter the distance between tube passes. The temperature field for the length L2 equal to 15.1 mm and fin spacing of 0.5 mm is shown in Figure 4 (a-c). The temperature field for the length L2 equal to 18.1 is reported in Figure 6 (a-c). The outlet temperatures are 333 K, 350 K and 365 K for the inlet velocities of 0.5 m/s, 0.75 m/s and 1.0 m/s. The increased length L2 is not that much suggestible, because the outlet flue gas temperature is reducing for all the velocities.

Figure 6:Static temperature contours when the space between the fins s = 0.5 with effect of L2 (a) v = 0.5 m/s (b) v = 0.75 m/s (c) v = 1.0 m/s

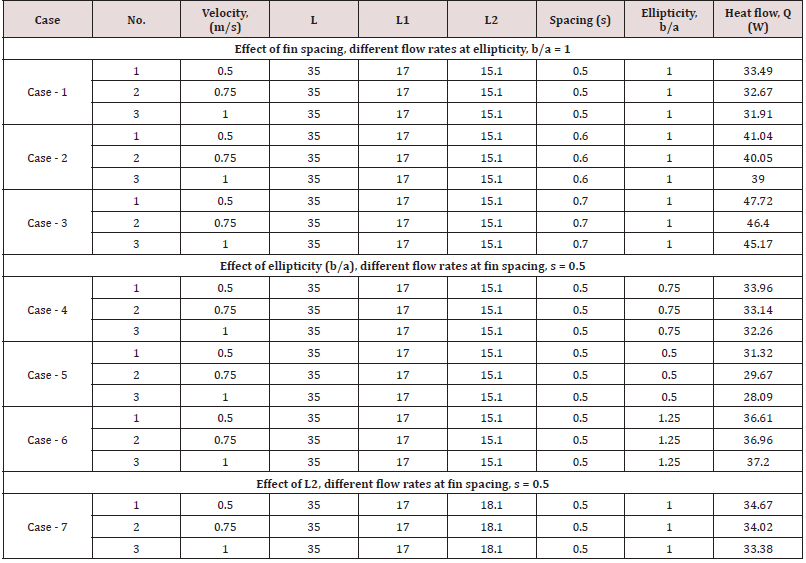
Based on the temperature profiles, the amount of heat flow through the fin is calculated from the below equation and the values are presented in (Table 2).
Q=kA(ΔT)/L (7)

Table 2: Heat flow through the fin at various fin geometry.

From the (Table 2), the ellipticity of the tube b/a = 1 and at flow rate of 0.5 m/s, the highest heat flow through fin is achieved. Whereas the ellipticity of the tube b/a = 0.5 and at flow rate of 1.0 m/s, the lowest heat flow through fin is achieved.

Figure 7: Total pressure contours when the tube ellipicity, a/b = 1 with effect of space between the fins (a) s = 0.5, v = 0.5 m/s (b) s = 0.5, v = 0.75 m/s (c) s = 0.5, v = 1.0 m/s (d) s = 0.6, v = 0.5 m/s (e) s = 0.6, v = 0.75 m/s (f) s = 0.6, v = 1.0 m/s (g) s = 0.7, v = 0.5 m/s (h) s = 0.7, v = 0.75 m/s (i) s = 0.7, v = 1.0 m/s

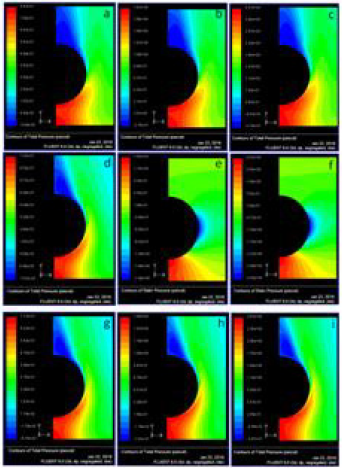
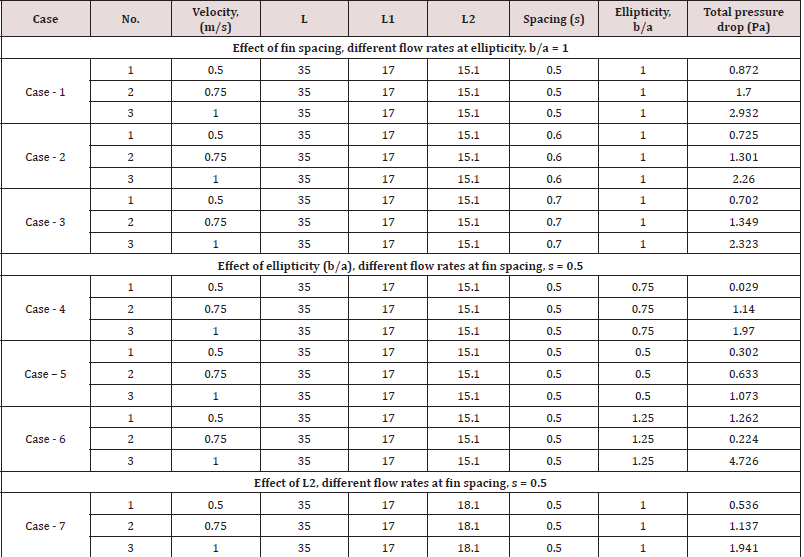
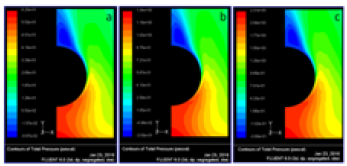
The total pressure is the pressure measured by bringing the flow to rest isentropically (without loss). The total pressure contours (Pa) at velocity of flue gases 0.5 m/s, 0.75 m/s and 1.0 m/s at fin spacing, s = 0.5 mm and at tube ellipticity, a/b = 1 were shown in (Figure 7) (a-c). It is observed from the figure, with the increase of velocity of flue gases increases, the total is decreasing. Similarly, the total pressure contours (Pa) at velocity of flue gases 0.5 m/s, 0.75 m/s and 1.0 m/s at tube ellipticity, a/b = 1 and at fin spacing, s = 0.6 mm and s = 0.7 mm were shown in Figure 7 (d-f), Figure 7 (g-i) respectively. The effect of total pressure on ellipticity is also studied. (Figure 8) (a-i) represents the total pressure contours at fin spacing s = 0.5 mm with effect of ellipticity at various velocities. (Figure 9) (a-c) represents the total pressure contours when the space between the fins s = 0.5 with effect of L2. The total pressure drop across the flow area for all the cases are summarized in (Table 3).

Figure 8: Total pressure contours when the space between the fins s = 0.5 with effect of ellipicity (a) a/b = 0.75, v = 0.5 m/s (b) a/b = 0.75, v = 0.75 m/s (c) a/b = 0.75, v = 1.0 m/s (d) a/b = 0.5, v = 0.5 m/s (e) a/b = 0.5, v = 0.75 m/s (f) a/b = 0.5, v = 1.0 m/s (g) a/b = 1.25, v = 0.5 m/s (h) a/b = 1.25, v = 0.75 m/s (i) a/b = 1.25, v = 1.0 m/s

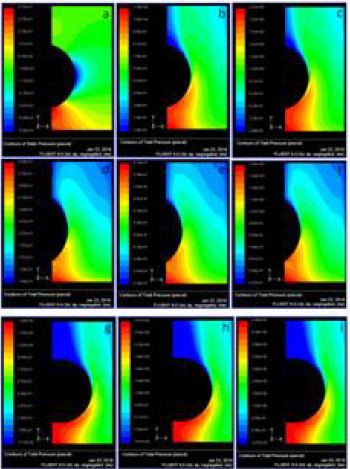
Figure 9: Total pressure contours when the space between the fins s = 0.5 with effect of L2 (a) v = 0.5 m/s (b) v = 0.75 m/s (c) v = 1.0 m/s

Table 3: Pressure drop through the fin at various fin geometry.

The present work focus on the heat flow and total pressure distribution across the plate fin and tube heat exchanger has been analyzed by using FLUENT software. The prototype of the plate fin and tube heat exchanger is designed in GAMBIT software and exported to FLUENT software for solving purpose. The study consists of several cases of fin geometry such as fin tube center, fin height; fin spacing and tube ellipticity are investigated, numerically. The following conclusions are drawn from the analysis. The distance between fins has an important effect on pressure drop. For the fin geometry with ellipticity value of 0.75 has the smallest static and total pressure drops. Since flue gas velocity is decreased, the lower pressure drop value is obtained. The ellipticity of the tube b/a = 1.25 and at flow rate of 1.0 m/s, the highest pressure drop across the fin is achieved. The ellipticity of the tube b/a = 1 and at flow rate of 0.5 m/s, the highest heat flow through fin is achieved. Whereas the ellipticity of the tube b/a = 0.5 and at flow rate of 1.0 m/s, the lowest heat flow through fin is achieved. Greater heat transfer and pressure drop values are obtained as the fin height is increased, due to the increased heat transfer surface area. The decrease in tube spacing causes the increase in heat transfer and decrease in pressure drop. As ellipticity increases in a tube, the heat transferred across a heat exchanger increases.

1. Shepherd DG (1956) Performance of one-row tube coils with thin-plate fins, low velocity forced convection, Heating, Piping Air Condition 28: 137-144.
2. Schulemberg F (1966) Finned elliptical tubes and their applications in air-cooled heat exchangers. J Eng Ind 88(2): 179-190.
3. Kayansayan N (1993) Heat transfer characterization of flat plain fins and round tube heat exchangers, Exp. Thermal Fluid Science 6(3): 263-272.
4. Jang JY, Wu MC, Chang WJ (1996) Numerical and experimental studies of three-dimensional plate fin and tube heat exchangers. Int J Heat Mass Transfer 39(14): 3057-3066.
5. Wang CC, Chang YJ, Hsieh YC, Lin YT (1996) Sensible heat and friction characteristics of plate fin-and-tube heat exchangers having plate fins. Int J Refrigeration 19(4): 223-230.
6. Beecher DT, Fagan TJ (1987) Effects of fin pattern on the air-side heat transfer coefficient in plate finned-tube heat exchangers, ASHRAE Transactions 93: 1961-1984.
7. Kays WM, London AL (1984) Compact Heat Exchangers, 3rd (Eds) McGraw-Hill, New York
8. Achaichia A, Cowell TA (1988) Heat transfer and pressure characteristics of flat tube and louvered plate fin surfaces, Exp. Thermal Fluid Science 1: 147-157.
9. Achaichia A, Cowell TA (1988) A finite difference analysis of fully developed periodic laminar flow in inclined louver arrays. In: Proceedings of the 2nd U.K. National Heat Transfer Conference, Glasgow, UK 2: 883-888.
10. Webb RL, Trauger P (1991) Flow structure in the louvered fin heat exchanger geometry, Exp. Thermal Fluid Science 4(2): 205-217.
11. Sahnoun A, Webb RL (1992) Prediction of heat transfer and friction for the louver fin geometry, J. Heat Transfer, vol. 114(4): 893-900.
12. Rocha LAO, Saboya FEM, Vargas JVC (1997) A comparative study of elliptical and circular sections in one and two row tubes and plate fin heat exchangers. Int. J. Heat Fluid Flow 18(2): 247-252.
13. Kundu B, Das PK (1997) Optimum dimensions of plate fins for fin-tube heat exchangers. Int. J. Heat Fluid Flow 18(5): 530-537.
14. Romero-Mendez R, Sen M, Yang KT, McClain R (2000) Effect of fin spacing on convection in a plate fin and tube heat exchanger, Int J Heat Mass Transfer 43(1): 39-51.
15. CC Wang, KY Chi (2000) Heat transfer and friction characteristics of plain fin-and-tube heat exchangers, part I: new experimental data, Int J Heat Mass Transfer 43(15): 2681-2691.
16. Wang CC, Chi KY, Chang CJ (2000) Heat transfers and friction characteristics of plain fin-and-tube heat exchangers, part II: Correlation, Int J Heat Mass Transfer 43(15): 2693-2700.
17. Saboya SM, Saboya FEM (2001) Experiments on elliptic sections in one and two row arrangements of plate fin and tube heat exchangers, Exp. Thermal and Fluid Science 24(1-2): 67-75.
18. Torikoshi K, Xi G, Nakazawa Y, Asano H (1994) Flow and heat transfer performance of a plate fin and tube heat exchanger (1st report: effect of fin pitch), 1994, Proc. 10th Int. Heat Transfer Conference, Brighton, UK 1: 411-416.
19. Erek A, Ozerdem B, Bilir L, Ilken Z (2005) Effect of geometrical parameters on heat transfer and pressure drop characteristics of plate fin and tube heat exchangers, Applied Thermal Engineering, vol. 25(14-15): 2421-2431.
20. Abu Madi M, Johns RA, Heikal MR (1998) Performance characteristics correlation for round tube and plate finned heat exchangers Int J Refrigeration 21(7): 507-517.
21. Gnielinski V (1976) New equations for heat and mass transfer in turbulent pipe and channel flow, International Chemical Engineering 41(1): 8-16.
22. Versteeg HK, Malalasekera W (1995) An introduction to computational fluid dynamics: The Finite Volume Method, John Wiley & Sons Inc New York
23. Shih T, Liou WW, Shabbir A, Yang Z, Zhu J, et al. (1995) A new k-ε eddy viscosity model for high Reynolds number turbulent flows. Computational Fluids, 24(3): 227-238.
24. Launder BE, Sharma BI (1974) Application of the energy-dissipation model of turbulence to the calculation of flow near a spinning disc. Letters in Heat Mass Transfer 1: 131-138.
25. Patankar SV (1980) Numerical heat transfer and fluid flow, Hemisphere Publishing Corporation, USA.