A note on the Burger’s method Volume 1 - Issue 3

Doo-Sung Lee*

• Department of Mathematics College of Education, Konkuk University, Seoul, Korea

Received: November 30,2020   Published: February 10, 2021

Corresponding author: Doo-Sung Lee, Department of Mathematics College of Education, Konkuk University Seoul, Korea

DOI: 10.32474/JOMME.2021.01.000116

 

Abstract PDF

Abstract

The existence and uniqueness of the solutions to an infinite system of nonlinear equations arising in thedynamic analysis of large deflection of a plate are discussed. Under the assumption that the rim of the plate is prevented from inplane motions, explicit equation for the coupling parameter is given.

Keywords: Existence, uniqueness, Berger’s method.1991 Mathematics Subject Classification. 46(Functional analysis),73(Mechanics of solids)

Introduction

In the analysis of classical mechanics problems, there are cases where linear mathematical model can not fully describe the phenomena. If the deflection of the plate is of order of magnitude of its thickness, the differential equations for the deflection and displacements can be written in terms of nonlinear equations. These nonlinear equations are usually difficult to obtain the solution. Thus several attempts have been tried to obviate the difficulties.
Among these attempts, it was Berger’s method which drew much attention.
Berger[1] derived a simplified nonlinear equations for a plate with large deflections by assuming that the strain energy due to the second invariants of the middle surface strains can be neglected when deriving the differential equations by energy method. Berger restricted his analysis to static and isotropic cases. Later, his procedure was generalized to dynamics of isotropic plates by Nash and Modeer [2] and to dynamic phenomena in anisotropic plates and shallow shells by Nowinski [3]. Berger’methods is dealt in recent books [5, 6].
There many are papers giving explicit solutions to various cases, however the search for the existence and uniqueness of the solution is rare, thus it is the purpose of this paper to discuss this matter.
The governing equations are

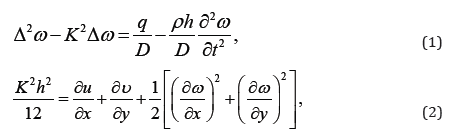
where w = deflectiom of plate in the normal direction. u, v =displacement in plane of plate.

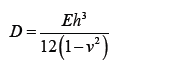
E = modulus of elasticity.
The coupling parameter is now determined from the equation (2) as follows, under the assumption that the rim of the plate is prevented from inplane motions

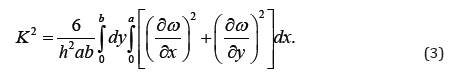
We attempt to find Fourier series solutions to (1) when q = 0 and the plate is simply supported.

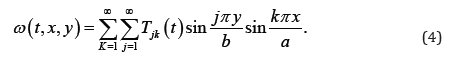
When this solution is substituted in (1) and (3) we find

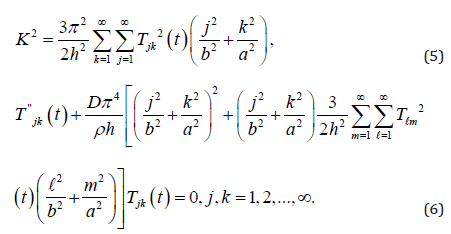
We discuss the existence and uniqueness of the solutions to above infinite system of nonlinear equations. The initial conditions on (6) will be taken as

If we multiply (6) by T’ jk and sum j, k from 1 to infinity, we can show that

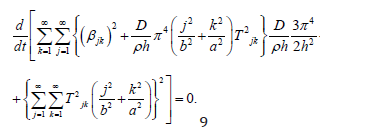
At first glance it would appear that if the initial conditions (7) and (8) satisfy a finite energy
condition, i.e.,

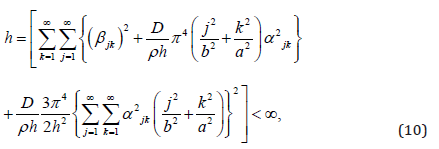
then (6) should have a solution for all t > 0. Indeed this is the case for finite system of the form

(6) since the finite system

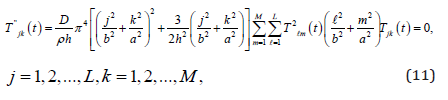
has associated with it a Lipschitz constant. Therefore, successive approximation method may be applied to prove the existence of solution to (11). However, the infinite system of equations (6) is not Lipschitz continuous since the coefficients of Tjk is unbounded as j, k → ∞. Thus the method of successive approximation fails and an alternative procedure is necessary.

In section 2, it will be shown that under the initial conditions (7) and (8) solution of the finite system (11) converge to a solution (6) as L, M → ∞. In section 3 it will be shown that the solution of (6) satisfying initial conditions (7) and (8) is unique.

Existence

To prove solution existence of (6), we define a set of functions Tjk,LM in the following way: For j, k ≤ L, M, Tjk,LM is a solution of the finite system of equations (11) satisfying the initial conditions (7) and (8) for j = 1, 2, · · · , M and k = 1, 2, · · · , L and for j > L, k > M set Tjk,LM = 0. The functions Tjk,LM are solutions of the infinite system (6),i.e.

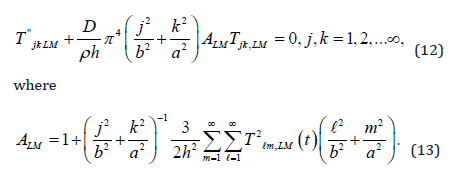
If in addition the initial data (7) and (8) satisfy the finite energy condition (10) it follows that

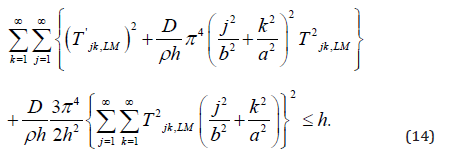
Thus there exist constants M1, M2 and M3 independent of L, M

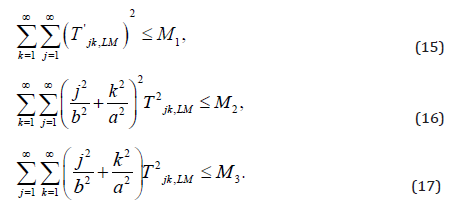
Lemma 1. |A’LM| is uniformly bounded independent of L, M where prime indicates differentiation with respect to t.
Proof. After differentiating the function ALM, if we employ Schwarz inequality we obtain

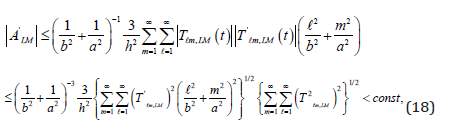
in view of the relations (15) and (16).
Lemma 2. |ALM| is uniformly bounded independent of L, M
Proof. |ALM | is uniformly bounded independent of L, M from the relation (17).
Thus ALM is uniformly bounded and equicontinuous; by Arzela’s lemma, there exists a subsequence {ALM,i} which converges uniformly to a continuous function A(t). Let Tjk be the solution of the(linear) equation

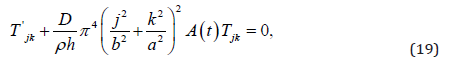
satisfying the initial conditions (7) and (8). The existence of solutions to (6) is settled by the

following theorem.

Theorem 1. The infinite system of (6) have a solution satisfying the initial data (7) and (8). Proof. It is only necessary to show that the solutions of linear system (19) furnish a solution of system (6). For this purpose it suffices to show that

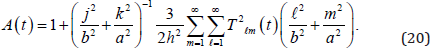
The series which occurs in (20) converges since(cf.(17))

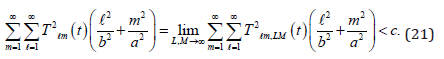
The equality in (20) follows from the estimate

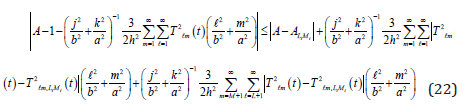
The right side of (22) can be made arbitrarily small by first choosing L, M, then choosing Li, Mi.

Uniqueness

In this section it will be shown that the infinite system (6) has at most one solution satisfying the initial conditions (7) and (8). We write (6) in the following way.

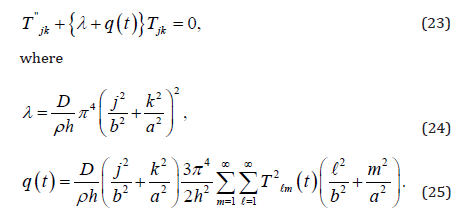
Let T_jk and S_jk be solutions of (6) satisfying the initial conditions (7) and (8) i.e. T_jk is the solution of (23) with q(t) being given by (25) and S_jk is the solution of

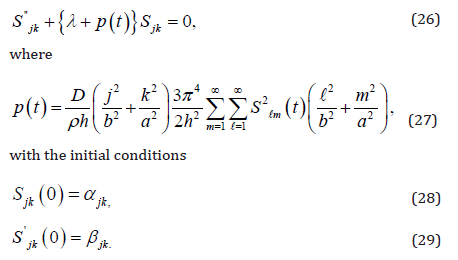
If we multiply (23) by Sjk and from the resulting equation, we substract (26) multiplied by Tjk and integrate it from zero to infinity, we get, after integrating by parts

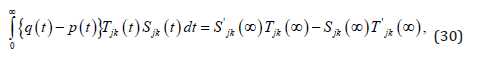
where we have used the initial conditions (7),(8),(28),(29). According to Gel’fand and Levitan[4] there exists function K(t, x) having continuous partial derivatives of first and second order such that

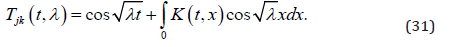
If we substitute (31) into (23),we find that the partial differential equation

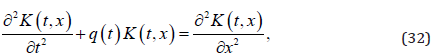
and the boundary conditions

are satisfied. Similarly,

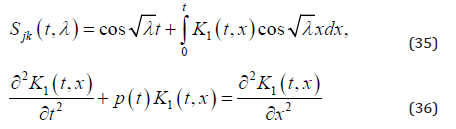
and the boundary conditions

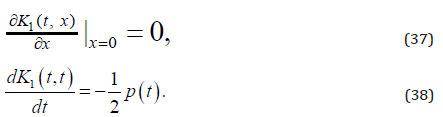
Thus if we substitute (31) and (35) into (30), we find that

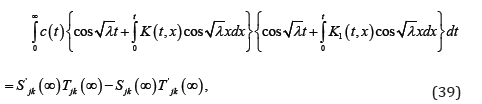
where c(t) = q(t) − p(t). Making change of variables and changing the order of integration in (39) we get

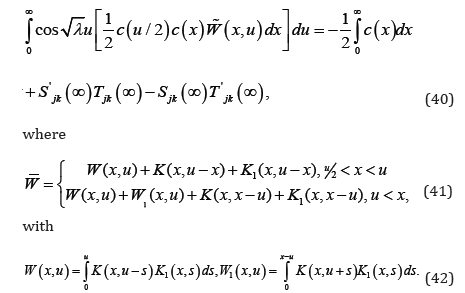
The left hand side of (40) is a function of λ,whereas right hand side is a constant. The equality holds only when both sides are equal to zero. Thus

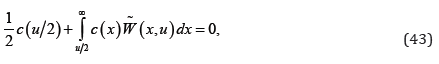
and from Gronwall’s Lemma we get c(t) = 0, i.e.,

Let U_j = K_j − S_j . We show U_j = 0 in the following. From (23) and (26) we have

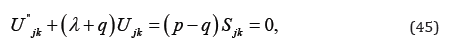
because of (44). Let us denote

Then Vjk(t) will be the solution of

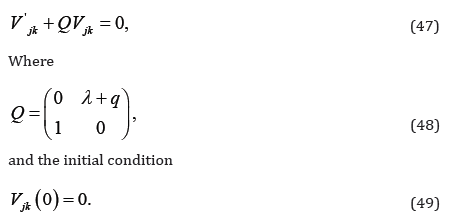
With the initial condition (49), the solution of (47) is Vjk = 0 from the semi-group theory. So we have the following theorem.
Theorem 2.The system of equations (6) have at most one solution satisfying the initial conditions (7) and (8).

References

1. HM Berger (1954) A new approach to the analysis of large deflections of plates, JApplMech. 22(1955): 465-472.
2. WANash and JR Modeer (1960) Certain approximate analyses of non-linear behavior of plates and shallow shells, ProcSymp, ThThin ElShells, Interscience, New York, USA.
3. JLNowinski (1975) Some static and dynamic problems concerning non-linear behavior of plates and shallow shells with discontinuous boundary conditions. IntJNon-Linear Mechanics 10(1): 1-14
4. IM Gel’fand and BM Levitan (1955) On the determination of a differential equation from its spectral function. Amer MathSocTrans Ser 15(4): 253-304
5. ARoy and RKBera (2019) Linear and nonlinear deformations of elastic solids. CRC press, Taylor & Francis Group.
6. FBloom and DCoffin (2000) Handbook of Thin Plate Buckling and Postbuckling, Chapman & Hall/CRC New York, USA.