Determination from First Principles of The Melting Point and Temperature Dependence of the Theoretical Strength Volume 3 - Issue 3

Zakarian D* and Khachatrian A

• Frantzevich Institute for Problems of Materials Science NAS Ukraine, Kiev

Received: October 26, 2020;   Published: November 19, 2020

*Corresponding author: Zakarian D, Frantzevich Institute for Problems of Materials Science NAS, Ukraine

DOI: 10.32474/MAMS.2020.03.000165

Abstract PDF

Abstract

A method has been developed for calculating the melting temperature of materials from first principles based on the temperature dependence of the theoretical strength. An analytical regularity of the temperature dependence of the theoretical strength of materials (metals, multielement metal alloys, borides, diamond-like covalent and ion-covalent crystals, quasi-binary eutectic systems) is obtained. The resulting ratio allows one to estimate the theoretical strength of materials in the temperature range from zero to the melting point.

Keywords: Theoretical strength; temperature dependence; melting point; pseudopotential method; quasi-harmonic approximation

Introduction

There is a scatter in the data on the melting temperature of refractory materials even in the case of sufficiently pure materials [1]. Often tabular data differ from each other by 300K or more (for example, in the case of TiB₂). Therefore, it is relevant to clarify the melting point from first principles, without using of experimental data. In this work, the method of a priori pseudopotentials [2-7] is used as the most suitable for the conditions of ab initio and computational speed. To calculate the physical characteristics, it is necessary to have the values of the energy of the electron-ion system of the material depending on the parameter of the crystal lattice or its volume. The total energy of the material can be represented as the sum U₀ of the energies of the electron-ion system at a temperature T=0 and U_T, the energy of thermal vibrations of ions at a temperature T ≠ 0

U =U₀ +U_T (1)

U₀ is calculated from first principles in the second order of perturbation theory, and the energy of thermal vibrations can be considered using one of the approximate methods - Debye or Einstein. Debye's model works better at low temperatures, while Einstein's model describes well the heat capacity of crystals at room and higher temperatures [2]. For problems concerning the problem of superconductivity, only Debye's method is suitable. When studying the temperature dependence of the mechanical characteristics of crystals, it is more convenient to use the Einstein model, especially when it comes to systems with a complex structure (multielement metal alloys and transition metal borides). According to Einstein's model, all atoms vibrate at the same frequency, which is proportional to the elastic characteristics of the material. Elastic characteristics are determined using the pseudopotential method. When calculating the energy of thermal vibrations (T ≠ 0), we use the quasi-harmonic approximation in combination with the method of a priori pseudopotential; as a result, we obtain the dependence of the energy of the electron-ion system on temperature through the volume of the unit cell

U =U (Ω (T) [4]

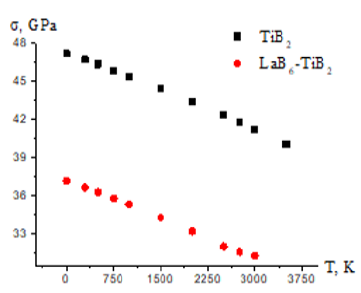
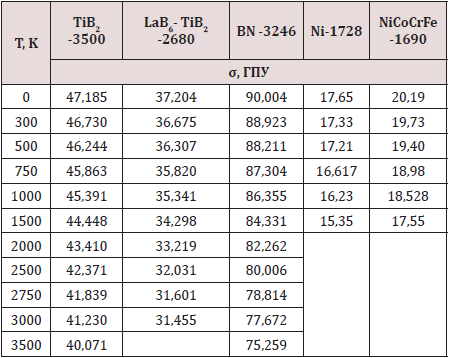
The developed model in the quasi-harmonic approximation allows, within the framework of the harmonic approximation, to calculate the parameters of the crystal lattice during thermal expansion, and then the corresponding physical and mechanical characteristics of materials. Strength and elastic characteristics represent the derivatives of the total energy with respect to the lattice parameter. To calculate the melting point of materials, we solve the inverse problem. Using the example of materials with a verified melting point, we determine the dependence of the theoretical strength on temperature using the pseudopotential method and the quasi-harmonic approximation [4]. The results of such a calculation are presented in tabular and graphical (Figure 1) form. Table 1 shows the results of calculations for representatives of the class of metals - metal alloys, borides, diamond-like materials, and eutectic systems. As the results of calculations show, for all crystalline materials (borides, carbides, metals, alloys, multielement alloys), the theoretical strength has a maximum value at temperature T = 0 K and decreases with increasing temperature. At maximum temperatures for all studied materials, the strength is 84.59 - 85.4% of the maximum strength.

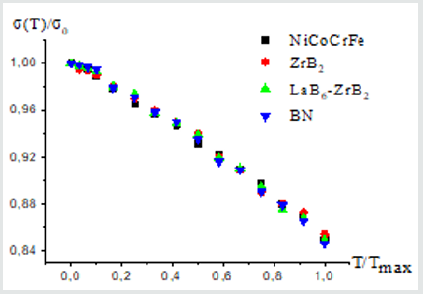
 In [1], it was experimentally proved that the high strength of boride and cermet eutectic systems is preserved up to a temperature of 0.8 T_max (T_max is the melting point), which was theoretically confirmed in our calculations from first principles [2,3]. (Figure 2) based on the calculation results (Table 1), shows the dependence of relative strength σ(T)/σ₀ on the parameter T/T_max for different materials for which the experimental values of the melting temperature (T_max) are known. According to mathematical analysis, the dependence of σ(T)/σ₀ on T/T_max can be approximated by a function of the type:

σ (T) / σ ₀ = 1 − 0,123T / T_max − 0, 027 (T / T_max)²

Here σ₀ is the strength at T = 0 K, σ (T) is the strength at the current temperature. At the melting point (T = T_max), the strength is σ(T_max) ≈ 0,85 σ₀.

Note that the T_max value is not used in the process of calculating the temperature dependence of strength from first principles. This means that with an unknown value of the melting point of the material, it is necessary to find the temperature dependence of the strength in the range (σ₀ – 0,85∙ σ₀). The corresponding temperature Т_х, at which σ (Т_х) ≈ 0,85 σ₀ will be the sought melting temperature Т_х ≈ Т_max. According to the data presented in table. for TiB₂ σ (Т3500) = 0.8492 σ₀, for the eutectic system 2500 < Т_max <2750 K, etc. As a result, formula (2) was obtained, which describes the temperature dependence of the theoretical strength of materials. The dependence of the relative theoretical strength σ(T)/σ₀ on T/T_max has the same form for different classes of materials. Knowing the melting point and the value of the theoretical strength at T = 0, using formula (2), makes it possible to calculate the strength of the material at any temperature. As for the theoretical strength σ₀, it can be calculated from first principles [5-7].

References

1. Ordanyan SS (2009) Prospects for creating new ceramics for mechanical engineering. Chemical Journal of Armenia 62(5): 547-556.
2. Zakaryan DA (2018) First-principles methods for calculating the physical characteristics of refractory binary eutectic composites. Thesis for doctor’s degree by specialty solid state physics. Institute for Problems of Materials Science of the National Academy of Science of Ukraine, Kyiv.
3. Zakarian D, Kartuzov V, Khachatrian A (2017) First principles simulation of temperature depandence of the strength in the quasi binary systems LaB₆ - MeB₂ with taking into account interfacial interaction. Metal Powder Report, Elsevier 72(3): 195-199.
4. Zakarian D, Kartuzov V, Khachatrian A (2016) Quasiharmonic approximation model in the theory of pseudopotentials. Reports of the NAS of Ukraine 4: 55-61.
5. Zakaryan DA, Kartuzov VV, Khachatryan AV (2015) Calculation of the basic physical and mechanical characteristics of highly entropic metal alloys. Mathematical models and computational experiment in materials science. 17: 56-61.
6. Zakarian D, Kartuzov V, Khachatrian A (2016) Preduction of the Mechanical Properties of LaB6 –ZrB2 Materialsin View of the Effect of Their Intercomponent Boundaries. Strenght of Materials. Springer. 48(2): 290-293,
7. Zakarian D, Kartuzov V (2006) Calculation of the theoretical strength of diamond-like materials based on the interaction energy of atomic planes. - Reports of the NAS of Ukraine. 7: 94-99.