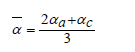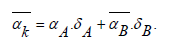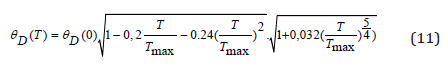Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2641-6921
Review Article(ISSN: 2641-6921) 
Calculation of Thermophysical Characteristics from First Principles Volume 3 - Issue 4
Zakarian D* and Khachatrian A
- Frantzevich Institute for Problems of Materials Science NAS, Kiev, Ukraine
Received: November 22, 2020; Published: December 10, 2020
*Corresponding author: Zakarian D, Frantzevich Institute for Problems of Materials Science NAS, Kiev, Ukraine
DOI: 10.32474/MAMS.2020.03.000167
Abstract
Using the pseudopotential method and the quasi-harmonic approximation, the following are calculated: the coefficient of linear thermal expansion (CLTE), the Debye temperature and their temperature dependencies. The temperature dependence of both characteristics, after approximation, is presented in analytical form. The results were compared with known tabular data. To check the reliability of the results, the calculations were carried out for pure metals as well. The difference between the calculated and tabular data does not exceed 7.3%. The presented model for calculating the CLTE of multielement alloys adequately reflects the results of thermal expansion of materials, considering such effects as phase transitions or the appearance of a second phase.
Keywords: Coefficient of linear thermal expansion; temperature dependence; pseudopotential method; quasi-harmonic approximation; debye temperature
Introduction
Along with hardness and strength, thermophysical characteristics (Debye temperature and coefficient of thermal expansion) are of primary importance when classifying materials by their properties. In [1], the Debye temperatures of nickel-based alloys were determined by fitting (to obtain the temperature dependence of the force constants), which have values of 150–200 K. The results of theoretical calculations of the Debye temperature for the same alloys, but with the addition of the element Cu (FeCoNiCu, FeCoNiCuCr, FeCoNiCuMn) are in the range 400-470K [2]. As is known, the physical characteristics of alloys in the first approximation can be estimated according to the rule of mixtures, from which it follows that the results obtained in [1] contradict the rule of mixtures. Also, the acceptance of the Debye temperature as a material constant is questionable, since, it is associated with quantities such as elastic moduli and lattice parameters, which are temperature dependent. A similar temperature dependence of the Debye parameter was noted in [3]. To assess the residual stresses in materials, knowledge of the values of their thermal expansion coefficient and its temperature dependence is required. Experimental determination of the thermal characteristics of materials is a problem for multi-element alloys and materials with a complex structure. There is a disagreement in the data on the temperature dependence of the physical and mechanical characteristics [1,2,4]. Often, to assess the temperature dependence of a particular physical characteristic of alloys, empirical formulas are used with the method of fitting to some known experimental data [1,2]. An analysis of the results of these works confirms the difficulty of determining the temperature dependence of the physical and mechanical characteristics of metal alloys, borides, composites, both experimentally and theoretically. The purpose of this work is to estimate the thermal expansion coefficient, Debye temperature and their dependence on temperature from first principles. The work uses the method of a priori pseudopotential [5] as the most suitable for the conditions of ab initio and speed of calculations.
Theory and Method Of Calculation
To calculate the physical characteristics of materials (metals, multi-element metal alloys, borides, eutectic composites), the value of the energy of the electron-ion system is required. The total energy of the electron-ion system of a crystalline material can be represented as the sum of U0 - the energies of the electron-ion system at a temperature T = 0 and UТ - the energy of thermal vibrations of ions at nonzero temperature. When calculating the energy of the electron-ion system of crystals at zero temperatures, the pseudopotential method is used, and the energy of thermal vibrations can be considered using the Einstein model [6]. According to Einstein's model, atoms in a crystal lattice vibrate at the same frequency, the value of which is proportional to the stiffness of the material. The average value of the lattice vibration energy is determined by the equality
where the summation is carried out over all types of oscillations, and is the oscillation frequency (according to Einstein's model, for all q).
To calculate the energy UТ, you need the value of the vibration frequency, which is associated with the dynamics of the crystal lattice.
The lattice dynamics is described using the Lagrange formalism, where the kinetic and potential energy of the vibrating atom is expressed through the displacement of the atom from the equilibrium position. When calculating the energy of thermal vibrations (T≠0), we use the quasi-harmonic approximation in combination with the method of a priori pseudopotential; as a result, we obtain the dependence of the energy of the electron-ion system on temperature through the unit cell volume U = U (Ω (T)) [7]. The developed model in the quasi-harmonic approximation allows, within the framework of the harmonic approximation, to calculate the parameters of the crystal lattice during thermal expansion, and then the corresponding physical and mechanical characteristics of materials. Strength and elastic characteristics represent the derivatives of the total energy with respect to the lattice parameter.
Calculation and Discussion
The coefficient of linear thermal expansion
The lattice parameter in the equilibrium state, depending on temperature, is determined from the minimum energy of the electron-ion system. Thermal expansion coefficient is calculated by the formula:
Here aT, a0 are the parameters of the crystal lattice at temperatures T and at zero temperature.
In the case of anisotropy, the CLTE of the material can be represented in the form of generalized curves
where and - are the CLTEs along the a and c axes, respectively.
The calculation results for some materials are presented in Table 1. For all metals, the calculated CLTE values and their temperature dependenceies are consistent with the tabular data and data from [8], except for the NiCoFe alloy. According to experimental data, the FeCoNi alloy has an almost constant CLTE at temperatures above 200 K. This is explained by the fact that FeCoNi is a two-phase alloy containing a small amount of a centered cubic body (BCC) in an FCC matrix.
According to the results of our calculations, the CLTE value of the FeCrCoNiGa alloy is in good agreement with the experimental data from [9] up to a temperature of 750K. And at temperatures above 750K a high increase in the thermal expansion coefficient is observed in the experiment, which is associated with a possible structural bcc - fcc transition [9]. Taking this factor into account, the CLTE of the FeCrCoNiGa alloy with an fcc lattice was estimated Table 1. The fcc alloy has a higher CLTE value compared to the same bcc alloy. According to the data of [9] at T = 900 K its value reaches 22.75 ∙ 10-6 K-1, and according to our calculations, α = 20.1 ∙ 10-6 K-1. The divergence of the results obtained from ab initio methods and experiment is less than 11.6%. It can be argued that the presented CLTE calculation model for multielement alloys adequately reflects the results of thermal expansion of materials, considering such effects as phase transitions or the appearance of a second phase. A relationship is observed between the calculated CLTE values and the material melting point Тмах.
Table 1: Coefficients of linear thermal expansion of alloys with fcc and bcc structure, calculated using formula (2) and experimental data (in parentheses).
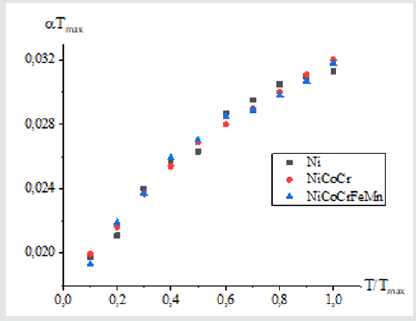
(Figure 1) shows the dependence of metals and multi-element alloys on the parameter T/Тмах. The same dependence of the function Y on the relative temperature parameter is obtained for metals and metal alloys considered in this work. As a result of mathematical analysis, two approximating functions were obtained that describe the functional dependence on x=T/Тмах:
Formula (3) is close to the empirical formula that was introduced in [10] to describe the temperature dependence of CLTE for austenitic steel in the temperature range 100-1600K, with the only difference that the Debye temperature was used instead of the parameter Тмах. The second approximation is simpler. When choosing an approximating function in the second case, the empirical relation was used to estimate the CLTE of metals with a cubic structure at room temperatures, which was proposed in [11]. The results obtained using approximations (3) and (4) agree with each other by 99%. We apply formula (4) to estimate the CLTE of borides, and in parallel calculate the CLTE from first principles. For eutectic composites, the calculation was carried out using the modified rule of mixtures [5]. In the usual rule of mixtures for calculating physical characteristics, interfacial interaction is ignored. The averaged CLTE of a composite is defined as the sum of the LCTEs of the components considering their volume fraction [12,13]:
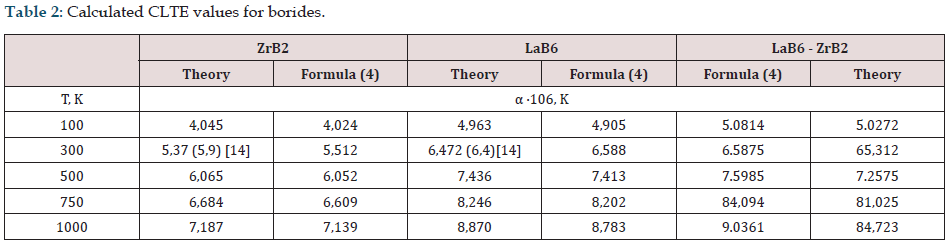
The results of CLTE calculations for borides and eutectics are presented in Table 2 For borides, the results obtained using relation (4) agree with experiment [14] and with the data obtained by us from first principles. In the case of composites, the maximum difference in CLTEs between calculated from first principles and using formula (4) is less than 7%.
Debye Temperature
In Debye’s theory, the frequency of acoustic waves is related to the speed of sound (s) and the wave number (qmax)
ωD = s.qmax (5)
The presence of optical phonons is neglected, and the Brillouin zone is replaced by a sphere of the same volume:
‘a’ is the crystal lattice parameter, and qmax represents the total number of allowed vectors in the Wigner - Seitz cell. The speed of propagation of vibrations is determined from the relation [6]
Here ρ is the density of matter, α^* - force constant, which is determined through the second derivative of the interatomic interaction energy with respect to displacements at the point of equilibrium position of the atom.
The Debye temperature is determined from the relation [6]:
Suppose that the generated elastic wave due to the vibrations of atoms propagates along the crystallographic directions (x, y or z axis), then the speed of propagation of elastic waves in isotropic bodies can be written in the form:
where ‘E’ is the modulus of elasticity at T = 0.
All physical characteristics (lattice parameter, elastic moduli, speed of sound) are determined at temperature Т0 = 0 for crystals and are presented in Tables 3,4,5. Experimental data obtained by other authors are also presented, and in parentheses there are known tabular values [8]. Calculations confirm the stability of the fcc structure for all alloys considered here Table 3 and the bcc structure Table 4. The Debye temperature for metals (Ni, Fe, Hf) was calculated using the same method. From the examples given, Hf has an hcp lattice. The calculated values of the elastic modulus and lattice parameter are consistent with experiment (the maximum difference between the calculated and experimental data is less than 7.3%) [5]. The elastic modulus for materials with a cubic crystal lattice is isotropic along the crystallographic directions (001) (along the x, y, z axes). To calculate the modulus of elasticity with an hcp lattice of Hf or TiB2, we assign these materials a cubic lattice, keeping the volume of the unit cell per two atoms for Hf or 3 in the case of TiB2. This approximation makes it possible to calculate the modulus of elasticity along the coordinate axes and obtain good results for the Debye temperature. The calculated values of the speed of sound and Debye temperature for pure metals are consistent with the tabular data.
Table 3: Calculated values of the lattice parameter, elastic modulus, speed of sound and Debye temperature for metals and multielement metal alloys with fcc crystal lattice.
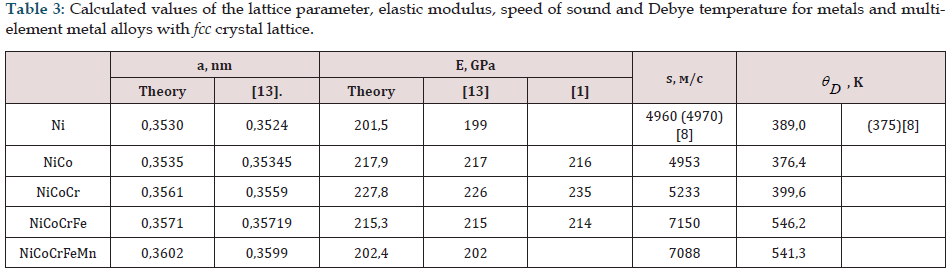
Table 4: Calculated values of the lattice parameter, elastic modulus, sound speed and Debye temperature of metals and metal alloys with a bcc crystal lattice.
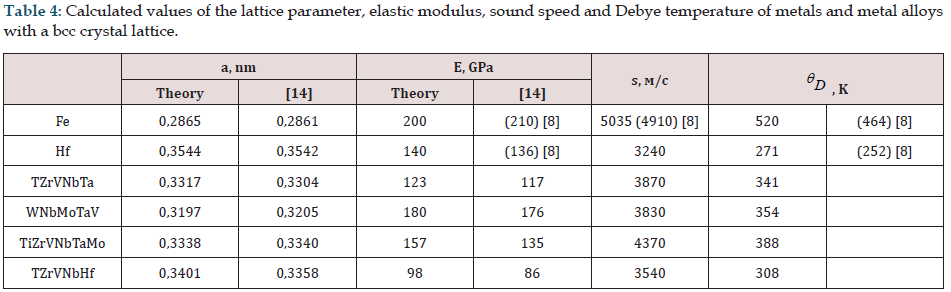
Table 5: Calculated values of the lattice parameter, elastic modulus, sound speed and Debye temperature of carbides and borides.

Debye temperature depends on temperature through the elastic modulus and lattice parameter (formulas 5-9). The calculated data Tables 3,4,5 refer to the temperature T = 0K. The temperature dependence of the Debye parameter can be represented as:
kBθD = h.s(T ).qmax (T ) (10)
or, taking into account the temperature dependence of the elastic moduli [15] and the coefficient of thermal expansion, we have:
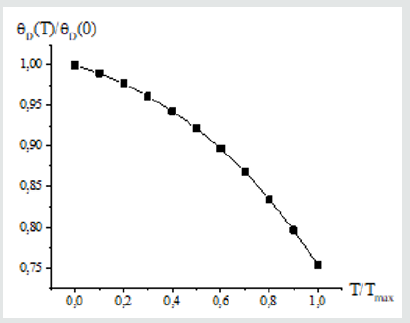
The calculation results are presented in (Figure 2). The temperature dependence of the Debye parameter depends on two competing factors arising, respectively, on Young’s modulus and lattice parameter. If the first factor decreases rapidly with increasing temperature, then the second factor slowly increases. Based on the results of our calculations of the temperature dependence of the Debye parameter (in the first approximation), only the temperature change in Young’s modulus can be considered.
Summary
The coefficient of linear thermal expansion of metals, metal multielement alloys, borides and eutectic boride-boride systems calculated from first principles (using the method of pseudopotentials and quasi-harmonic approximation) is presented in an analytical form depending on the melting point. With the help of the obtained formula, bypassing complex quantum-mechanical calculations, it becomes possible to estimate the CLTE for the family of the mentioned materials. From ab initio calculations, a formula was obtained that describes the temperature dependence of the relative Debye temperature θD(T ) /θD(0) onT / Tmax for different classes of materials.
References
- Laplanche G, Gadaud P, Bärsch C, Demtröder K, Reinhart C, et al. (2018) Elastic moduli and thermal expansion coefficients of medium-entropy subsystems of the CrMnFeCoNi high-entropy alloy. Journal of Alloys and Compounds 746: 244-255.
- Huijuan Ge, Hongquan Song, Jiang Shen, Fuyang Tian (2017) Effect of alloying on the thermal-elastic properties of 3d high-entropy alloys. Materials Chemistry and Physics 210: 320-326.
- Novikov VV, Avdashchenko DV, Mitroshenkov NV, Matovnikov AT (2014) Thermal expansion and lattice dynamics of RB compounds at low temperatures. - Physics of Solid State 56(10): 2069-2076.
- Wu, Zhenggang (2014) "Temperature and Alloying Effects on the Mechanical Properties of Equiatomic FCC. Solid Solution Alloys. " PhD diss., University of Tennessee.
- Zakarian DA (2018) First-principles methods for calculating the physical characteristics of refractory binary eutectic composites. Thesis for doctor’s degree by specialty solid state physics. - Isititue for Problems of Materials Science of the National Academy of Science of Ukraine, Kyiv.
- Ziman JM (1966) Principles of the Theory of Solids. Moscow: Mir 416 pp.
- Zakarian D, Kartuzov V, Khachatrian A (2016) Quasiharmonic approximation model in the theory of pseudopotentials. Reports of the NAS of 4: 55-61.
- Novickiy L. Kozhevnikov I (1975) Thermophysical properties of materials at low temperatures. Moscow, Mechanical engineering,
- Shuo Hang, Adam Vida, Anita Heczel, Wei Li (2017) Thermal expansion in FeCrCoNiGa high-entropy alloy from theory and experiment Applied Physics Letters 110, 241902.
- Van Bohemen SMC (2013) The nonlinear lattice expansion of iron alloys in the range 100-1600 K, Scripta Materialia 69: 315.
- Ryabukhin AG (1999) Linear coefficient of thermal expansion of metals. Physical chemistry and technology of inorganic materials 3:15-17.
- Zakarian D, Kartuzov V, Khachatrian A (2016) Production of the Mechanical Properties of LaB6 –ZrB2 Materialsin View of the Effect of Their Intercomponent Boundaries. Strength of Materials. Springer 48(2): 290-293.
- Zakarian D, Kartuzov V, Khachatrian A (2017) First principles simulation of temperature depandence of the strength in the quasi-binary systems LaB6 - MeB2 with taking into account interfacial interaction. Metal Powder Report, Elsevier 72: 195-199.
- Serebryakova TI, Neronov VA, Peshev PD (1991) High-temperature borides. - Moscow, Metallurgy 368 pp.
- Zakarian D, Khachatrian A, Firstov S (2019) Universal temperature dependence of Young’s modules. Metal Powder Report, Elsevier 74(4): 204-206.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...