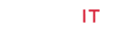On the Second Harmonic Index of Titania Nanotubes Volume 1 - Issue 1

Yingying Gao¹, Süleyman Ediz², Mohammad Reza Farahani³*, Muhammad Imran^4,5

• ¹Colleage of Pharmacy and Biological Engineering, Chengdu University, China
• ²Faculty of Education, Yuzuncu Yil University, Turkey
• ³Department of Applied Mathematics, Iran University of Science and Technology (IUST) Narmak, Iran
• ⁴Department of Mathematical Sciences, United Arab Emirates University, United Arab Emirates
• ⁵Department of Mathematics, School of Natural Sciences (SNS), National University of Sciences and Technology (NUST), Pakistan

Received: March 10, 2018;   Published: March 19, 2018

Corresponding author: Mohammad Reza Farahani, Department of Applied Mathematics, Iran University of Science and Technology (IUST) Narmak, Tehran, Iran

DOI: 10.32474/DDIPIJ.2018.01.000102

Abstract PDF

---

Abstract

Topological indices which are graph invariants derived from molecular graphs of molecules are used in QSPR researches for modeling physicochemical properties of molecules. Topological indices are important tools for determining the underlying topology of a molecule in view of theoretical chemistry. The second harmonic index has been defined recently. In this study we compute the second harmonic index of Titania nanotubes.

Keywords: Harmonic Index; Novel Harmonic Indices; Second Harmonic Index; Titania Nanotube

Introduction

Graph theory which is one of the most important branches of applied mathematics and chemistry has many applications from the basic sciences to the engineering sciences especially for solving and modeling of real world problems. Chemical graph theory is the common place for graph theory and chemistry. Topological indices are indispensable tools for QSPR researches in view of theoretical chemistry and chemical graph theory. Topological indices have been used more than seventy years predicting and modeling physicochemical properties of chemical substances. A graph G = (V,E) consists of two nonempty sets v and 2-element subsets of v namely E. The elements of v are called vertices and the elements of E are called edges. For a vertex v de^f0V) show the number of edges that incident to v. The set of all vertices which adjacent to is called the open neighborhood of and denoted by n (v). If we add the vertex v to n(v), then we get the closed neighborhood of v,n(v) . For the vertices u and v, d(u, v) denotes the distance between u and v which means that minimum number of edges between u and v. The largest distance from the vertex v to any other vertex u called the eccentricity of v and denoted by ^ev.

The first distance based topological index is the Wiener index which was defined by H. Wiener to modeling the boiling points of paraffin molecules [1]. In his study Wiener computed the all distances between the all atoms (vertices) in the molecular graph of paraffin molecules and named this graph invariant as "path number". The Wiener index of a simple connected graph G defined as follows:

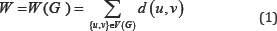
Many years later the path number renamed as "Wiener index" to honor Professor Harold Wiener for valuable contribution to mathematical chemistry. In t he same year, the first degree based topological index was proposed by Platt for modeling physical properties of alcanes [2]. The Platt index of a simple connected graph G defined as follows;

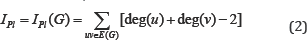
After these both studies, approximately twenty five years later the well-known degree based Zagreb indices were defined by Gutman and Trinajstić to modeling π-electron energy of alternant carbons [3]. The first Zagreb index of a simple connected graph defined as;

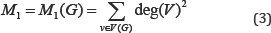
And the second Zagreb index of a simple connected graph defined as;

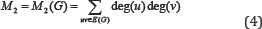
An alternative definition of the second Zagreb index of a simple connected graph is given the following formula:

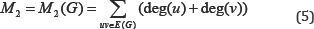
In 1975, Randić defined the "Randić index" [4] to modeling molecular branching of carbon skeleton atoms as follows:

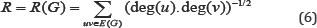
Among the all topological indices, the above mentioned topological indices have been used for QSPR researches more considerably than any other topological indices in chemical and mathematical literature. We refer the interested reader to the following citations for up to date information about these well- known and the most used topological indices [5-15].

Harmonic index of a simple connected graph G was defined by Zhong in 2012 [16] as follows

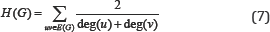
Since then, there are more than one hundred papers in mathematical and chemical literature about Harmonic index and its applications. We refer the interested reader to [17,18] and references cited in these articles.

The novel harmonic indices have been defined recently by the present authors [19]. In [19], the fifth harmonic index of H-Naphtalenic nanotube and TUC4 [m, n] nanotube were calculated.

Harmonic indices were defined in [20] as;

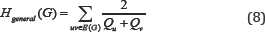
Where Qu is a unique parameter which is acquired from the vertex u ϵ (G).

The first kind of this Harmonic indices was studied by Zhong by considering ^Qu to be the degree of the vertex u:

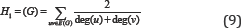
The second kind of this class was defined by considering ^Qu to be the number ⁿu of vertices of G lying closer to the vertex u than to the vertex v for the edge uv of the graph G:

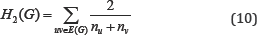
The third type of this class was defined by considering ^Qu to be the number ^mu of edges of G lying closer to the vertex v than to the vertex u for the edge uv of the graph G:

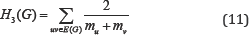
The fourth type of this class was defined by considering ^Qu to be the eccentricity of the vertex u:

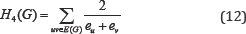
The fifth type of this class was defined by considering ^Quto be the: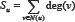

And the sixth type of this class was defined by considering Qu to be the: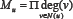

For topological indices of Titania nanotubes, we refer the interested reader [20-28] and references therein. The aim of this paper is to compute the exact value of the second harmonic index of Titania nanotubes.

Results and Discussion

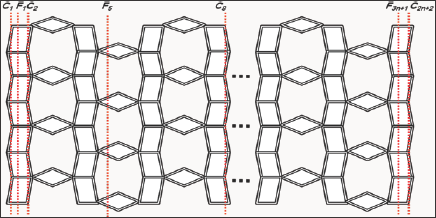
In this section we compute the exact values of the second harmonic index of Titania Nanotubes (Figure 1). Rezaei et al. [28] computed edge vertex version of Co-Pi index of Titania nanotubes [28]. The following table given the classifications of the vertices of TiO₂ [m,n] with respect to the parameter n_u . We get the results with the help of the article of Rezai et al. [30]. From the help of Table 1, we can state our main result (Figure 2).

Figure 1: A graphical figure of Titania Nano tubes TiO₂[m, n].

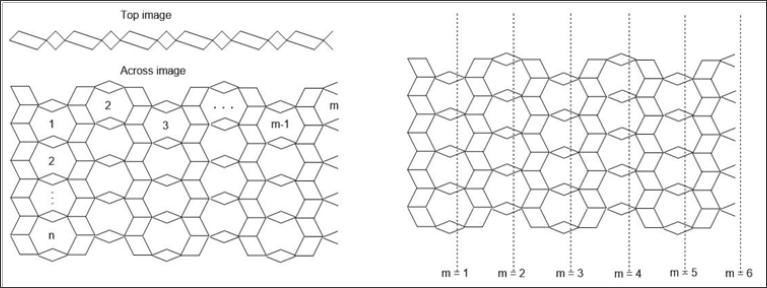
Table 1: The edge classification of the vertices of TiO2 [m, n] with respect to the parameter.

Figure 2: Orthogonal cuts representation of the Titania Nano tubes.

Theorem 1. The second harmonic index of Titania Nanotubes TiO₂[m ,n] is given as;

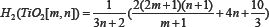
Proof. From the definition of the second harmonic index and Table 1, we can write that:

Conclusion

In this study we found the exact values of newly defined the second harmonic index of Titania nanotube. This calculation will help to predict and model some physicochemical, optical and biological properties of Titania nanotube. It can be interesting to compute the novel harmonic topological indices of some other nanotubes and networks for further studies. It can also be interesting to study the mathematical and QSPR properties of these novel harmonic indices.

References

1. Wiener H (1947) Structural Determination of Paraffin Boiling Points. J Am Chem Soc 69(1): 17-20.
2. Platt JR (1947) Influence of Neighbor Bonds on Additive Bond Properties in Paraffins. J Chem Phys 15(6): 419-420.
3. Gutman I, Trinajstić N (1972) Graph theory and molecular orbitals. Total φ-electron energy of alternant hydrocarbons. Chem Phys Lett 17(4): 535-538.
4. Randić M (1975) Characterization of molecular branching. J Am Chem Soc 97(23): 6609-6615.
5. Gutman I (2013) Degree-based topological indices. Croat. Chem Acta 86: 315-361.
6. Garcia I, Fall Y, Gomez G (2010) Using Topological Indices to Predict Anti- Alzheimer and Anti-Parasitic GSK-3 Inhibitors by Multi-Target QSAR in Silico Screening. Molecules 15(8): 5408-5422.
7. Furtula B, Gutman I, Dehmer M (2013) On structure-sensitivity of degree-based topological indices. Appl Math Comput 219(17): 89738978.
8. Hao J (2011) Theorems about Zagreb Indices and Modified Zagreb Indices. MATCH Commun. Math Comput Chem 65: 659-670.
9. Li X, Shi Y (2008) A Survey on the Randic Index 1 Introduction. MATCH Commun. Math Comput Chem 59: 127-156.
10. Xu K, Liu M, Das KC, Gutman I, Furtula B (2014) MATCH Commun. Math Comput Chem 71: 461-508.
11. Klavzar S, Deutsch E (2015) M-Polynomial and Degree-Based Topological Indices. Iran J Math Chem 6(2): 93-102.
12. Li X, Gutman I (2006) Mathematical Chemistry Monographs, University of Kragujevac, Kragujevac, Serbia.
13. Dobrynin AA, Entringer R, Gutman I (2001) Wiener Index of Trees: Theory and Applications. Acta Appl Math 66(3): 211-249.
14. Kier LB, Hall LH, (1986) John Wiley & Sons, New York, NY, USA.
15. Gutman I, Das KC (2004) The first Zagreb index 30 years after. MATCH Commun. Math Comput Chem 50: 83-92.
16. Zhong L (2012) The Harmonic Index for Graphs. Appl Math Lett 25: 561566.
17. Nazir R, Sardar MS, Zafar S, Zahid Z (2017) Edge Version of Harmonic Index and Polynomial of Some Classes of Bridge Graphs. Bull Int Math Virtual Inst 7(2): 363-371.
18. Onagh BN (2017) The harmonic index of subdivision graphs. Trans Combin 6(4): 15-27.
19. Farahani MR, Ediz S, Imran M (2017) On novel harmonic indices of certain nanotubes. International Journal of Advanced Biotechnology and Research 8(4): 277-282.
20. Gao W, Farahani MR, Jamil MK, Siddiqui MK (2016) The Redefined First, Second and Third Zagreb Indices of Titania Nanotubes TiO₂ [m,n]. The Open Biotechnology Journal 10: 272-277.
21. Farahani MR, Jamil MK, Imran M (2016) The vertex Pi index of Titania Nanotubes TiO₂ (m,n). Vertex Appl Math Nonlinear Sci 1: 170-175.
22. Farahani MR, Kumar RP, Kanna MR, Wang S (2016) The vertex Szeged index of Titania Nanotubes TiO₂(m,n) . Int J Pharm Sci Res 7: 3734-3741.
23. Farahani MR, Kanna MR, Kumar RP, Jamil MK (2016) Computing Edge Co-Padmakar-Ivan Index of Titania Nanotubes TiO₂ (m,n). Journal of Environmental Science, Computer Science and Engineering & Technology 5(3): 285-295.
24. Munir M, Nazeer W, Nizami AR, Rafique S, Kang SM (2016) M-Polynomials and Topological Indices of Titania Nanotubes. Symmetry 8(11): 117.
25. Li Y, Farahani MR, Jamil MK, YING FANG LI (2016) The Edge-Szeged index of the Titania Nanotubes TiO₂(m,n). International Journal of Biology, Pharmacy and Allied Sciences 5: 1260-1269.
26. Nadeem I, Shaker H (2016) On Eccentric Connectivity Index of TiO2 Nanotubes. Acta Chim Slov 63: 363-368.
27. Liu JB, Gao W, Siddiqui MK, Farahani MR (2016) Computing three topological indices for Titania Nanotubes TiO₂[m;n]. AKCE International Journal of Graphs and Combinatorics 13(2016): 255-260.
28. Rezaei M, Farahani MR, Kamran MJ, Kashif A, Lee DW (2016) Vertex Version of Co-PI index of Titania Nanotubes TiO₂. Advances and Applications in Mathematical Sciences 15(8): 255-262.