
Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2644-1217
Research ArticleOpen Access
Biostatistical and Mathematical Analysis on Diversion Cover Plate During Covid-19 Pandemic Volume 4 - Issue 2
Bin Zhao1* and Xia Jiang2
1School of Science, Hubei University of Technology, Wuhan, Hubei, China
2Hospital, Hubei University of Technology, Wuhan, Hubei, China
Received: October 10, 2020 Published: October 20, 2020
*Corresponding author: Dr. Bin Zhao, School of Science, Hubei University of Technology, Wuhan, Hubei, China
DOI: 10.32474/OAJCAM.2022.04.000184
Abstract
Submarine sailing under the water, because of the attack, misoperation, equipment failure, collision, fire and other factors, the risk of wreck always exists. How to escape and how to carry out effective rescue is a problem that needs to be solved for the navy of submarine owner country since submarine came into being. In order to improve the ability to float out of danger, some submarines are equipped with gas blowing equipment or hydrazine blowing equipment (two kinds of chemical liquid mixed to produce a large amount of high-pressure gas) for emergency ballast jetting, so that the submarine quickly drainage up to float. Some submarines are equipped with quick drift escape device and collective escape with buoyancy ball, buoyancy cylinder, etc. In this paper, the motion characteristics of a simplified diversion cover plate used for buoyancy ball are studied and a differential equation solution is given during COVID-19 pandemic.
Keywords: The submarine; Guide plate; Movement characteristics
Introduction
As for the release device with the buoyancy ball, the resistance of the submarine in the course of moving is generally borne by the diversion cover plate above it. In case of danger, the diversion cover plate above the buoyancy ball needs to be unlocked by the mechanical locking device and can be opened smoothly and smoothly under the action of buoyancy. Therefore, it is of great significance to study the motion characteristics of fixed axis positive buoyancy diversion cover plate under water during COVID-19 pandemic [1].
Method
Building A Mechanical Model
There is a uniform rectangular plate completely submerged in water. The length, width and thickness of the rectangular plate are respectively L1 , L2 ,and . Let’s say the h density of the rectangle is pρ and the density of the water is w ρ The rectangular edge of length is L2 articulated to the underwater base, and the rectangular plate is initially fixed horizontally. Now the horizontal fixation of the rectangular plate is removed, and the motion characteristics of the rectangular plate in water need to be solved [2].
Analysis and solutions
There is a dynamic moment formed by gravity and buoyancy for the rectangular plate rotating at a fixed axis in the water (assumed to be Ma ). When the rectangular plate moves in the water, it will be affected by the resistance of water flow and form ar esistance moment (assumed to be MR ). The inertia moment of the rectangular plate is assumed to be Mm . Then, the equation of fixed-axis motion can be expressed as:
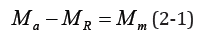
Suppose θ(t) is the rotation Angle of the rectangular plate at any time t .
For a uniform rectangular plate, the center of buoyancy coincides with the center of gravity. The dynamic moment formed by buoyancy and gravity can be expressed as:
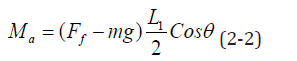
Where, Ff is buoyancy, mg is gravity of the rectangular plate, m is mass of the rectangular plate, and g is gravitational acceleration.
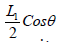

Substituting equations (2-3) and (2-4) into equation (2-2) can be obtained:
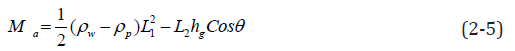
It is assumed that in the process of rotation of the rectangular plate in water, the resistance of water flow is the same at the position equidistant from the rotation center. The resistance moment formed by the resistance of water flow can be expressed as:
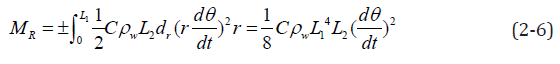
Where, is the C water resistance coefficient. Since the resistance of water flow is always opposite to the direction of motion, when
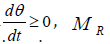
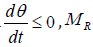
The moment of inertia of the rectangular plate can be expressed as

Where, I is the rotational inertia of the rectangular plate, which can be expressed as:
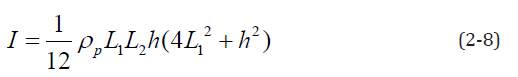
Substituting Equation (2-8) into Equation (2-9) can be obtained
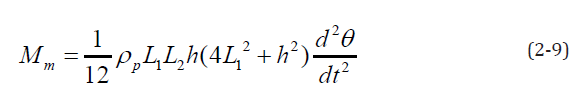
Formula (2-5), (2-6) and (2-9) are substituted into formula (2- 1) and can be obtained
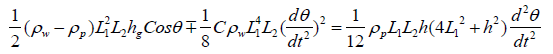
The above equation can be simplified to obtain:
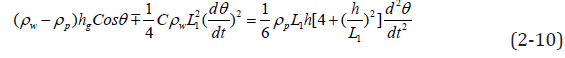
It can be seen from the above equation that the equation is independent of the width L2 of the rectangular plate, which also means that the motion characteristics of the rectangular plate in water are independent of the width of the rectangular plate. Divide both sides of equation (10) by
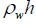
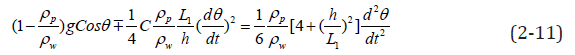
When the ratio of plate density to fluid density is
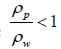
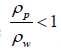
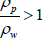
Results
The difference method is used to solve the problem. It is assumed that the time interval [0,T] is evenly divided into several time intervals, with a single interval of ΔT. Suppose that t = 0 at time(i) = t1, the initial condition is
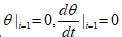
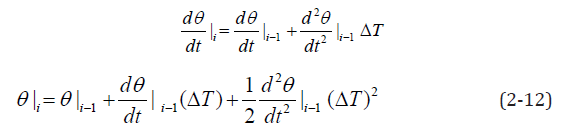
Conflict of Interest
We have no conflict of interests to disclose, and the manuscript has been read and approved by all named authors.
Acknowledgement
This work was supported by the Philosophical and Social Sciences Research Project of Hubei Education Department (19Y049), and the Staring Research Foundation for the Ph.D. of Hubei University of Technology (BSQD2019054), Hubei Province, China.
References
- Jiang Zhiqiang, Li Weijia, Pan Zhi, Jia Zhichun (2021) A Vector Control Mechanism for Nozzle of Diversion Plate Underwater Vehicle. China Water Transportation 22(4): 44-46.
- Xianlin Zeng, Yiguang Hong (2018) Distributed Algorithm for Robust Resource Allocation with Polyhedral Uncertain Allocation Parameters. Journal of Systems Science and Complexity 31(1): 103-119.
- G Wang, GB Giannakis, YC Eldar (2018) Solving Systems of Random Quadratic Equations via Truncated Amplitude Flow. IEEE Transactions on Information Theory 64 (02): 773-794.
- G Wang, L Zhang, GB Giannakis, M Akcakaya, J Chen (2018) Sparse Phase Retrieval via Truncated Amplitude Flow. IEEE Transactions on Signal Processing 66 (02): 479-491.
- Shuxin Ding, Chen Chen, Bin Xin, Jie Chen (2018) A Bi-objective Load Balancing Model in a Distributed Simulation System Using NSGA-II and MOPSO Approaches. Applied Soft Computing 63(04): 249-267.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...




