To characterize A- optimal row-column designs for complete Diallel Cross method (2) Volume 2 - Issue 5

Sharma MK* and Mohammad O Ibrahim

• Department of Statistics, Addis Ababa University, Addis Ababa

Received: May 14, 2020;   Published: June 22, 2020

*Corresponding author: M K Sharma, Department of Statistics, Addis Ababa University, Addis Ababa, Ethiopia

DOI: 10.32474/CTBB.2020.02.000146

Abstract PDF

Abstract

The purpose of this paper is to characterize A-optimal designs for complete diallel cross (CDC) method (2) for conducting an experiment with ‘p’ inbred lines when heterogeneity is to be eliminated in two directions. Some methods of construction of this design are given. AMS Subject Classification: 62 k 05

Keywords: Complete diallel cross; Latin square; Row-column design; Nested balanced incomplete block design; General combining ability; Optimality

Introduction

By a complete diallel cross (CDC) mating design is one in which a set of p inbred lines is chosen and crosses among these lines are made. The procedure gives rise to a maximum of p2 combinations. Griffing (1956) gave four classifications of CDC mating designs as : CDC method (1) mating design contains P² crosses, CDC method (2) mating design contains p( p +1) / 2 crosses, CDC method (3) mating design contains p(p-1) crosses and CDC method (4) mating design contains p( p −1) / 2 crosses. The CDC mating designs are often of interest to breeders to investigate the genetic properties and potentials of inbred lines of individuals (for application in plant breeding see, Hallaur and Miranda, 1988). When the experimenter is interested in comparisons of hybrid with their parents, it is advisable to include the parents in the experimental material in the experiment and use CDC method (1) or (2) so that comparisons of hybrid with the parents can be made [1] Suppose there are p inbred lines and it is desired to perform a CDC experiment involving v = p( p +1) / 2 crosses of the two types (i × j) and (i × j) for i, j = 0,1,....., p −1 , where cross (i × j) = ( j × i) . This is the CDC method (2) mating design of [1] with p inbred lines, having p self and p( p −1) / 2 distinct F1 crosses, who gave the detailed analysis of such mating designs laid out in a randomized complete block design. Most commonly, CDC mating design have been evaluated using completely or randomized complete block designs as environment designs. In most cases, however, the number of crosses is too large, leading to an overall inefficient experiment. It is for this reason incomplete block designs were introduced by many authors to resolve the problem of estimating the genetic parameters precisely. However, this approach is not quite appropriate if one is interested in statistical properties, like optimality, of the design. Even an optimal incomplete block design may turn out to be of poor efficiency when used for a CDC experiment. This is because, the analysis of a CDC experiment in incomplete blocks depends on the incidence of inbred lines, rather than on that of treatments or crosses in blocks. Several authors such as [2-9] investigated optimal block designs for CDC method (4) in the 1-way elimination of heterogeneity. [10,11] constructed A- optimal block design for CDC method (2) by using mutually orthogonal Latin squares and nested balanced incomplete block design, respectively, in the 1-way elimination of heterogeneity. The most of the available literature restricts to universal optimality and combinatorial aspects for CDC experiment method (4) and method (2) in the 1-way elimination of heterogeneity set up except [12-13] who studied CDC method (4) in row-column ( 2-way elimination of heterogeneity) designs. However, row-column designs for complete diallel cross method (2) have not received any attention so far in statistical literature. The primary objective of this paper is to characterize the optimal row-column designs for CDC method (2). Here we are giving some methods of construction of these designs through Latin squares and nested balanced incomplete block designs. Row-column designs control heterogeneity in the experimental material in two directions. Therefore it increases the precision of the estimates of genetic parameters. The paper is organized as follows. In section 2 we give some preliminary results. In section 3 we give the condition of characterization of these designs. In section 4 we describe the method of analysis of these designs. In section 5 we give the condition of A- optimality of these designs. In section 6 we describe the efficiency factor of these designs in comparison to randomized block designs. In section 7 we give several methods of construction of these designs.

Preliminaries

Suppose that we wish to conduct the diallel cross experiments involving p inbred lines giving rise to a total of nc = p( p +1) / 2 distinct crosses of the types i × i and (i × j) for i, j = 0,1, 2,....., p −1 , where cross (i × j) = ( j × i) , in a row-column design with a ≥ p rows and b ≥ p columns. This is the complete diallel cross (CDC) method (2) of [1], having p self and p( p −1) / 2 distinct F1 crosses, where p is a prime or power of a prime or prime factors , who gave the detailed analysis of such mating designs laid out in a randomized complete block design. Assume that only one cross of the type i×j = j ×i and i×i , where i, j = 0,1, 2,....., p −1 , are applied in each of the N = a b plots. We assume the usual fixed-effects additive linear model.

y_{(i j)} kl = μ + g_i + g_j + β_k + γ_l + e_(ij) k l (4.1)

Let y_{(i j)}kl = be the observation on (i × j) cross applied in the kth row and lth column, μ is grand mean effect, gi (gj) is the ith (jth) line gca effect, βk is the kth row effect, γ_l is the lth column effect and the e(ij) k l are uncorrelated random errors with zero mean and constant variance. The various effects are assumed to satisfy the side conditions.

It is of interest to estimate the general combining ability contrast between ith and jth lines g j , i, j = 0,1,. . . p −1. In order for these contrast to be estimable, a necessary condition is that v ≤ ab, where v = p ( p +1) / 2. Let, (i, j = 0, 1, . . ., p −1)denote the corresponding least squares estimators of g_j , i, j = 0,1,. . . p −1

Definition: On the above criterion , a design in which p( p +1) / 2 crosses are allocated in an a × b array, is a design for CDC method (2) if the least square estimators of gca effects of ith and jth lines gi - gj contrast, i, j = 0,1,....., p −1 , satisfy

Var(gˆ_i-gˆ_j) = δ² σ² i j = … p − (4.2)

where δ2 is some constant and depend on the particular design employed.

Characterization of CDC Method (2) Design

Consider a row-column design d having mik incidences of ith line in the kth row and nil incidences of ith line in the lth column (0 ≤ i ≤ p −1, 1 ≤ k ≤ a, 1 ≤ l ≤ b). Let M = {m_ik}and N = {nil }denote row and column incidence matrices, respectively. Further let ri = be the number of replication of ith r=(r₁,r₂,...r_p) treatment, is a row vector of the replications, r ii′ is the number of crosses in d in which i and i′ lines appear together and

We then have the following theorem.

Theorem: A design in which p( p +1) / 2 crosses are allocated in an a × b array is a design for CDC method (2) if the least square estimators of the difference of gca′s of two lines, say, i and j i.e gi - gj , i, j = 0,1,....., p −1 , contrasts satisfy

Proof. Consider a diallel cross experiment method (2) involving p lines in a row-column design d with k rows and l columns. The model (2.1) can be written in the matrix form as

Y = μ l_n+ Δ′₁ g + Δ′₂ β + Δ′₃ γ+e (5.1)

Where Y is an N × 1 vector of observed responses, μ is the general mean, g , β and γ are the column vectors of p general combining ability (gca) parameters, a row effects and l column effects, respectively, are the corresponding design matrices, respectively Ä_′(N × p), Ä₂′(N×k), Ä₃′(N×l) and e denotes the vector of independent random errors having mean 0 and covariance matrix σ 2 IN. The various effects are assumed to satisfy the side conditions

Let G_d = Δ₁ Δ₁′ = (g_dii'),g_dii' = s_di=r_i i.e the number of times ith line occurs in the crosses in the whole design d and for i ≠ i , gdii′ is the number of crosses in d in which i and i′ lines appear together, M = Δ₁Δ′₂ be the p × k incidence matrix of lines vs rows, N = Δ₁Δ′₃ be the p × l incidence matrix of treatments vs columns and Δ₂Δ′₃ = 1_l1′_l. Let r dc denote the number of times the c th cross appears in the design d, c = 1, 2, . . . , v and similarly ri denote the number of times the ith line occurs in the design d, i = 0, 1, . . . p-1 . Under (4.1), it can be shown that the reduced normal equations for estimating the treatment effects, after eliminating the effect of rows and columns, are

Where
Where Cd is a p × p information matrix of the lines and G_d = Δ₁ Δ₁′ = (g_dii), M = (m_ik) is the number of times the line i occurs in row k of d , N = (n_il ), is the number of times the cross i occurs in the column l. Thus, the entries of Cd are

Using equations (4.3) and (4.4), we get variance of (gˆ_i − gˆ_j ) as given below.

Hence theorem is proved.

Analysis of CDC Method (2) Design

We next consider the analysis aspects of CDC method (2) designs. Let

Note that these designs are not orthogonal but are variance balanced. Hence the analysis of these designs is simple. The analysis of variance (ANOVA) for CDC method (2) is given below in Table 1.

Note: The specific combining effects and its sums of squares can also be obtained by using above row-column design for CDC method (2) design [10]

Condition of A-Optimality CDC Method (2) Design

It is not easy to construct A-optimal CDC method (2) design. It is easier to construct CDC method (2) designs that possess some additional symmetry properties e.g. (i) Designs must be equireplicate in lines. (ii) The number of crosses in which two lines appear together must be equal. (iii) In addition the number of rows and columns should be equal. Let us take a Latin square of standard form with p symbols [14]. If we identify the symbols of a Latin square as lines of a CDC method (2) and perform crosses among the lines appearing in same cell in the first row and also perform crosses between the lines of the first row from corresponding lines in other rows. Thus we get a block design d for CDC method (2) involving p( p +1) / 2 crosses of the type (i × i) and (i × j) , where i, j = 0,1,....., p −1 . The crosses of the type (i × j) = ( j × i) occurs two times in a design d while crosses of the type (i × i) occurs once in a design d. The above block design can be arranged in p rows and p columns. Then we get a row- column design d* with parameters v = p ( p +1) / 2, b = p and a =p. In d*

the design is orthogonal with respect to lines, row vs blocks as classification or a row-regular setting with respect to lines , for i, j = 0,1,....., p −1 , k = 1, . . ., p.

nd*i..l = x where x = int( mk/p) = 2 i.e the lines appear two times in columns as blocks, the design is orthogonal with respect to lines , blocks vs rows as a classification, where m =2.

A design d *ε D is said to be A-optimal if and only if tr (V_d*) ≤ tr( V_d) means that trace of variance –covariance matrix d *ε D is less than equal to trace of variance –covariance matrix d.
Now we give the following theorem without proof [13]

Theorem 5.1: Let d *ε D( p, b, k ) be a row – column design for diallel crosses satisfying

where x = [2k/p], Ip is an identity matrix of order p and 1p 1′p is a p × p matrix of all ones. Furthermore, using d *ε D( p, b, k ) all elementary contrasts among gca effects are estimated with variance

Then according to Kiefer (1975), d* ɛ D (p, b, k) is universally optimal and , and in particular minimizes the average variance of the best linear unbiased estimator of all elementary contrasts among the gca effects.
By using equations (5.3) and (5.4) we obtain the information matrix Cd*

(7.1)

Where Ip is an identity matrix of order p and 1p is a unit column vector of order p.

The information matrix Cd* is a completely symmetric matrix and its trace = 2(p-1)2, is greater than the trace (Cd) = 6p given in Theorem (7.1) (i) and also it variance = 1/p-1 is less than the variance of Cd = 2(p-1)/6p given in (iii). Hence our proposed design d* is A- optimal.

Efficiency Factor

Efficiency of any design is always compared with no other design except randomized block design. Suppose that instead of the proposed design d*, one adopts a randomized complete block design with 2 blocks, each block having all p( p +1) / 2 crosses. [1] on page 473 shows that the variance of any elementary contrast among the gca effects is 2σ₁²/ (p + 2), where σ1 2 is the per observation variance in the case of a randomized block design experiment. It is clear from (5.3) that using design d* each elementary contrast among gca effects is estimated with variance σ₁² / ( p −1) . Hence the efficiency factor of design d* compared to a randomized block design under the assumption of equal intra block variances is given by

(8.1)

Hence our proposed design is more efficient than randomized block design when p > 4.

Methods of Construction D*

Here we are giving some methods of construction of these designs by using Latin squares which possess the above property and also by using some NBIB designs giving by [15] For definition of Latin square and NBIBD [14,15], respectively.

a. Method: Let p = 2m+1 ,m ≥ 2 . Then cyclically developing the following 2m +1 columns

(0, 2m), (1, 2m−1), (2, 2m− 2), . . . , (2m, 0)

Yields a row-column for CDC method (2) with parameters v = p ( p +1) / 2 , b = p and a =p.

Remark 1. The m columns form a NBIBD with parameters p = 2m +1, b1 =m,

k₁ = m 2m+1 , k+ = 2 , λ₂ = 1.

Example 1. For m =2, we get the following row-column design for CDC method (2) with parameters v = 15, b =5 and a =5.
Row-Column Design for CDC method (2)

b. Method: Start with a self – orthogonal Latin square and its transpose; See [16]. Superimpose one over other then we get a row-column design for CDC method (2) with parameters v = p (p+1)/2, b = p and a = p.

Example 2: Consider the following self –orthogonal Latin square and its transpose of order 5. After superimposing, we get row-column design for CDC method (2) with parameters v = 15, b =5 and a =5.

c. Method: [10] constructed optimal block design for CDC method (2) by superimposing two mutually orthogonal Latin squares of order p. From their designs row-column designs for CDC method (2) with parameters v =15, b = 5 and a =5 can be obtained. The plan is given below.
Row-Column Design for CDC method (2)

Remark 2. Our proposed design consumes less experimental units in comparison to [10]

Method: [17,18] obtained mutually orthogonal Latin squares of order 12 (3×4) and 10(2×5), superimposing these Latin squares we can obtain row-column designs for CDC method (2) with parameters v = 78, b =12 and a =12 and v = 55, b =10 and a =10.

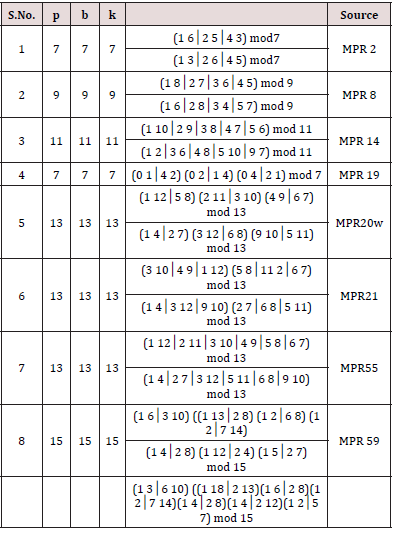
d. Method. [15] gave NBIBD with parameters (p, b1, b2, r, k1, k2) where k₁ = p −1, k₂ = 2 and p = b1. If p is odd, a starter [19,20] in an abelian group of order p is a partition of the non-zero elements of the group into pairs x_i, y_i (i =1, 2,..., (p – 1) / 2) such that the (p-1) differences (x_i –y_i ) and (y_i– x_i ) are all different. The p-1 differences are thus the p-1 non-zero elements of the group. With only a slight change, a starter can thus be used to produce the initial block in the representation of an NBIBD with b₁ = p, k₁ = p −1 and k₂ = 2 . We searched these designs from the catalogue of MPR (2001) and listed in Table 1. These designs can be used for the construction row-column designs for CDC method (2). We are giving example below for the construction of row-column design for CDC method (2).

Example 3: Consider the S.No.1 NBIBD from Table 2 with parameters p = 7, b =7 and k =7. We see that there are two distinct starters. We put these starters vertically and cyclically developing mod (7) and attaching the cross of the type i× i in a column where the ith does not occur Then we get a row-column design for CDC method (2) with parameters v = 28, b = 7, and a =7 as given below.

Remark 3. From the designs constructed by Method 1 and Method 4, one can obtain row-column design foe CDC method (2) with parameters v = p ( p +1) / 2, a = ( p +1) / 2, b = p .

References

1. BGriffing(1956) Concept of general specific combining ability in relation to diallel crossing systems. Aust J Biol Sci 9: 463-493.
2. S Gupta,S Kageyama (1994) Optimal complete diallel crosses. Biometrika . 81: 420-424.
3. A Dey, Midha, Chand K (1996) Optimal designs for diallel crosses. Biometrika 83(2): 484-489.
4. R Mukerjee(1997) Optimal partial diallel crosses. Biometrika 84(4): 937-946.
5. FS Chai,R Mukerjee (1999) Optimal design for diallel crosses with specific combining abilities. Biometrika 86(2): 453-458.
6. ADas, A Dey, A Dean (1998) Optimal design for diallel cross experiments. Statist Prob Letters 36(4): 427-436.
7. R Parsad R,VK Gupta,R Srivastava (1999)Optimal designs for diallel crosses. JourSocStat Comp and Application1: 35-52.
8. MK Sharma(2004) Optimal complete diallel cross. Advances in Mating Designs Chapter 15.
9. Sharma M K, FantaSileshi (2010) Optimal block designs for diallel crosses. Metrik71: 361-372.
10. MK Sharma, Fanta Sileshi (2011) Optimal Block Designs For CDC experiments (2). Metron 69(3): 297-307.
11. MK Sharma, M Tadesse(2016)Optimal block and row-column designs for CDC methods. Sankhya SerB 1-14.
12. S Gupta, C Choi (1998) Optimal row-colmn designs for complete diallel crosses. Commun Statist Theory Meth 27(11): 2827-2835
13. R Parsad,VK Gupta ,Gupta, Sudhir (2005) Optimal Designs for Diallel and Double Cross Experiments. Utilitas Mathematica68: 11-32.
14. D Raghavarao (1971)Constuction and Combinatorial Problems in Design of Experiments. JWiley and SonsNew York USA.
15. JPMorgan, DA Preece, DH Rees (2001) Nested balanced incomplete block designs. Discrete Mathematics 231(1-3): 351-389.
16. ASHedayat (1973) Note: Self Orthogonal Latin Square Designs and their importance. Biometrics: 29 (2): 393-396.
17. B Mann Henry(1942) The Construction of Orthigonal Latin Squares. The Annals of Mathematical Statistics 13(4): 418-423.
18. Parker (1959) Orthognal Latin Squares. Mathematics 45: 860-862.
19. WD Wallis(1988) Combinatorial designs. Mercel DekkerNew York USA.
20. WD Wallis(1992) One factorization if Complete Graphs in: JHDinitz DR Stinson (Eds)Contemporary design Theory- a collection of surveys Wiley.593-631.