Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2644-1381
Review Article(ISSN: 2644-1381) 
Semi-Balanced Array and CDC method (4) Volume 2 - Issue 4
MK Sharma* and Mohammed Omer
- Department of Statistics, Addis Ababa University, Ethiopia
Received: March 27, 2020; Published: April 21, 2020
*Corresponding author: M K Sharma, Department of Statistics, Addis Ababa University, Addis Ababa, Ethiopia
DOI: 10.32474/CTBB.2020.02.000142
Abstract
With a large number of lines in a complete diallel cross experiments method (4), the number crosses become unmanageable to be accommodated in homogeneous blocks. To overcome this problem incomplete block designs for complete diallel cross Griffing’s method (4) with replication 2 and 1 have been proposed by using semi balanced arrays (p (p-1)/2, p, p, 2), where p is an odd prime or power of an odd prime. The analysis of data obtained through proposed design is presented. The analysis includes the analysis of variance, estimation of general combining ability and of specific combining ability. The analysis is illustrated with the help of numerical data. Table of universally optimal block designs has been provided.
Keywords: Orthogonal Array; Semi-Balanced Array; Complete Diallel Cross; Block Design; Optimality
Introduction
Rao (1973) [1] gave method of construction of semi-balanced array of strength 2. These arrays have been used in the construction of resolvable balanced incomplete block design. We are using these arrays in the construction of complete diallel cross (CDC) method (4)A common experimental design in genetics is the diallel, in which pairs of distinct lines are cross bred in order to estimate genetic effects [2]. Let p denote the number of lines, where p is an odd prime or power of odd prime, and it is desired to perform a diallel cross experiment involving v = 1/2p(p-1) crosses of the type (i x j) between lines i and j , where i< j = 1,…, p. This is the CDC method (4) mating design with p inbred lines. [2] discussed in detail the analysis of this design in randomized block design (RBD). Later incomplete block designs were introduced by many authors See Singh et al. [3] to resolve the problem of estimating the genetic parameters precisely. The problem of generating optimal block designs for CDC method (4) for the case where treatment differences are due to only general combining abilities (gca) has been investigated by several authors such as [4-9]. [10] Considered the case when specific combining ability (sca) effects are also present in the model. They defined balanced and orthogonal designs i.e designs that are (i) balanced for gca comparisons (ii) balanced for sca comparisons and (iii) orthogonal in the sense that the least- square estimates of any gca contrasts is uncorrelated with the least- square estimate of any sca contrast. They gave a necessary condition for adesign to be balanced and orthogonal. They further proved that a design is balanced and orthogonal if and only if, it is a triangular partially balanced incomplete design (TPBIB design). Choi et al. [11] showed that the several series [4-12] of designs, which are optimal for gca comparison, are also optimal when sca effects are also present in the model although they are not TPBIB design. The above series designs have only one replication for each cross. Choi et al. [11] also reported three series of new designs in which each cross is replicated only once. So due this drawback all the sca effects are not estimable in these designs. This necessitates the construction of optimal block designs for CDC method (4) by which one can estimate both gca and sca effects uncorrelated to each other from the model.In the present paper, we are deriving optimal incomplete block designs for CDC methods (4) through semi balanced arrays. From these designs we can derive two more design for CDC methods (4) by dividing the blocks into two groups, provided the total number of blocks is even. The above designs are found to be optimal in the sense of [13,14].The rest of this article is organized as follows: in section 2, we give some definitions. In section 3, we discuss Lemma without proof given by [15]. In section 4, we discuss the relation of semi-balanced array with designs for CDC method (4) with example. In section 5, we give method of analysis of these designs. In section 6, we discuss optimality of proposed design and efficiency factor in comparison to randomized block design. In section 6 and, we have explained the analysis with the help of numerical data and discussed results obtained from the example.
Some Definitions
a. Definition: According to [15], a (N, r, p) array is said to be
a semi-balanced array of strength d if for any selection of d rows α1,
α2, . . . , αd , we denote d rows by n(i1 , i2, . . ., id).
(i) n (i1 , i2, . . ., id) = 0 if any two ij are equal.
(ii) Σns( i1 , i2, . . ., id) =λ constant
Where s represents summation over all permutation of distinct
elements i1 , i2, . . ., id.
b. Definition: According to [4], a diallel cross design to be orthogonally blocked if each line occurs in every block r/b times, where r is the constant replication number of the lines and b is the number of blocks in the design.
Method of Construction of Semi-Balanced Array
A semi balanced array of strength 2 is useful in the construction of some combinatorial arrangements. The minimum value of N in such case is p (p-1)/2 with λ = 1. [15] gave following Lemma which gives the construction of semi balanced array (p (p-1)/2, p, p, 2) and also has maximum number of rows.
Lemma: Let p be an odd prime or an odd prime power in
which case there exists a Galois field with s elements, GF(s). Then
(p(p-1)/2, p, p, 2) semi balanced array exists.
For proof, see Rao(1973)
Relation between Semi-balanced Array (p (p-1)/2, p, p, 2) and Designs for CDC System
Consider a semi-balanced array (p (p-1)/2, p, p, 2), where p is an odd prime or power of odd prime. There are (p-1)/2 total sets in a semi-balanced array (p (p-1)/2, p, p, 2). If we identify the elements of semi- balanced array as lines of a diallel cross experiment and ignoring first row of each set perform crosses in any two sets among the corresponding columns appearing in the same two sets, we get a mating design for diallel cross experiment involving p lines with v =p (p-1/2)crosses, each replicated twice OR ignoring first row of each set and super imposing any two sets, we may also get a mating design for diallel cross experiment involving p lines with v =p (p-1/2)crosses, each replicated twice. Now consider rows as blocks, we obtain block design d for Griffing’s CDC method (4) with parameters v = p (p-1)/2, b =p-1, k =p, r =2. From this design we can derive two more designs for CDC experiment method (4) with parameters v = p (p-1)/2, b = (p-1)/2, k =p, r =1 by dividing the blocks in two groups containing first (p-1)/2 blocks in one group and last (p-1)/2 blocks in second group, provided the number of blocks should be an even integer.
Thus using the above procedure, we may obtain  different layouts designs for
Griffing’s CDC method (4). In block designs for Griffing’s CDC
method (4) each line occurs in every block r/b times and every
cross is replicated twice. According to Gupta et al. (1995) these
designs are orthogonally blocked. In an orthogonal design no loss
of efficiency on the comparisons of interest is incurred due to
blocking. A block design for which N = θ 1p 1′b is orthogonal for
estimating the contrasts among gca parameters, where N denotes
the line versus block incidence matrix and θ is some constant.Choi
et al [11] proved that orthogonally blocked designs remain optimal
for the estimation of gca comparisons even in the presence of sca
effects in the model when each cross is replicated twice. Designs for
method (4) are balanced for gca comparisons
different layouts designs for
Griffing’s CDC method (4). In block designs for Griffing’s CDC
method (4) each line occurs in every block r/b times and every
cross is replicated twice. According to Gupta et al. (1995) these
designs are orthogonally blocked. In an orthogonal design no loss
of efficiency on the comparisons of interest is incurred due to
blocking. A block design for which N = θ 1p 1′b is orthogonal for
estimating the contrasts among gca parameters, where N denotes
the line versus block incidence matrix and θ is some constant.Choi
et al [11] proved that orthogonally blocked designs remain optimal
for the estimation of gca comparisons even in the presence of sca
effects in the model when each cross is replicated twice. Designs for
method (4) are balanced for gca comparisons
Theorem: The existence of Semi -Balanced Array (p (p-1), p, p, 2) implies the existence of  orthogonally blocked
incomplete block design with parameters v = p (p-1)/2, b =p-1, k
=p and r =2 for [2]method (4).If the number of blocks is an even integer, then we may obtain
orthogonally blocked
incomplete block design with parameters v = p (p-1)/2, b =p-1, k
=p and r =2 for [2]method (4).If the number of blocks is an even integer, then we may obtain  orthogonally blocked
incomplete block design with parameters v = p (p-1)/2, b =(p-1)/2, k
=p and r =1 for [2]method (4).
orthogonally blocked
incomplete block design with parameters v = p (p-1)/2, b =(p-1)/2, k
=p and r =1 for [2]method (4).
Example 5.1; The present example of semi-balanced array for
p =5 has been taken from Rao (1973). If p =5, the residue classes 0,
1, 2, 3, 4 mod (5) form a field. We write the 5 elements of GF (5) as
0, ±1, ±2, and hence the key sets are.
(0, 1, 2, 3, 4), (0, 2, 4, 1, 3 ) (5.1)
second vector is obtained from the first on multiplying by 2.
Writing (4.1) vertically and generating the other columns by the
addition of elements GF (5). We obtain 10 columns as shown below
which is divided into two groups.

From the semi balanced array given above, we may obtain designs for Griffing’s CDC method (4) (i) by ignoring the first row and perform crosses in any two sets among the corresponding column appearing in the same two sets and developing columns mod (5) we get a mating design for diallel cross experiment OR superimposing one set to over other set. This mating design can be transformed into environmental design with parameters v =10, b =4, k =5 and r =2, by considering rows as blocks as given below.
Design for Griffing’s method (4)

From the above design, we may get two more incomplete block designs for CDC experiment method (4) with parameters v =10, b =2, k =5 and r =1. Taking blocks 1 and 2, we may get first design and taking blocks 3 and 4, we may get second design.
Analysis
For the analysis of data obtained from design d,we will follow two stage procedures for estimating gca and sca effects [16,17]. The first stage is to consider to estimate cross effects, τ =(τ2,...,τp(p−1/ 2))T = by the following linear model.
y = μ1+ Xτ + Dβ + e (6.1)
where y be n ×1 vector of observations, 1 is the n ×1 vector of ones, X is the n × v design matrix for treatments and D is an n × b design matrix for blocks, that is, the (h,u)th((h,l)th) element of X (respectively, of D) is 1 if the hth observation pertains to the uth cross ( to lth block ),and is zero otherwise (h = 1, …, n; u = 1, …, v ; and l = 1, … , b), μ is a general mean, τ is a v ×1vector of treatment parameters, β is a b ×1 vector of block parameters and e is an n ×1 vector of residuals. It is assumed that vectorβ is fixed and e is normally distributed with E(e) = 0 , V (e) =σ2I , where I is the identity matrix of conformable order. Following[18,19], the analysis of our proposed designs leads to the following reduced normal equations for the crosses for model (6.1).
Cdτ = Qd (6.2)
Where Cd= R−NK−1N '
AndQd= (Q1d,…., Qvd) = T - N K-1 B
In the above expressions R and K are diagonal matrices of order
v × v and b × b with common diagonal elements 2 and p, respectively.
N = X´D is the v × b incidence matrix of the designs d; T = X´ Y and
B = D´Y are vectors of cross totals and block totals of order v×1 and
b × 1 respectively for designs d.
Hence a solution to (6.2) is given by
τˆ = Cd −Qd
where Cdˉ is the generalized inverses of Cd with the property thatCC ˉ C = C. The sum of squares due to crosses are Q Cd Cdˉ QCd withd.f. = rank (Cd) for designs d with the expectation and variance of Qd being
E(Qd ) = Cdτ V (Qd )= σ2Cd (6.4)
Now we will utilize the above equations to estimate the genetic
parameters in the proposed design.
The second stage is to utilize the fact that the cross effects
can be expressed in terms of gca and sca abilities. So we can write
effects as follows:
τij = gi +gj +sij (6.5)
where g i(gj) is the gca for the ith (jth) parent and sij (sij = s ji) is
the sca for the cross between the ith and the jth parent ( i< j =0, 1, …
, p-1) and we also impose restrictions to solve equation (6.5) that is  for all i. In matrix notation equation
(5.5) can be written as
for all i. In matrix notation equation
(5.5) can be written as
τ = Zg + s (6.6)
where Z = (z u i) (u = 1, 2, …, v : i = 0, 1, …, p-1) is the cross and
gca relation matrix.
zui= 1 if the uth cross has only one parent = i’
= 0, otherwise.
and g = ( g1, …, gp)T s= and { s12, s12,...., sp(p − 1) / 2}T =.
Following the approach used in[20],the equation (5.6) can then
be written as
Cdτ = Cd Zg + Cds
i.e. E(Qd ) = Cd Zg + Cds (6.7)
Since the matrix Cd is singular, we use the unified theory of least squares due to [15]and replace the usual true inverse of variancecovariance matrix by a g-inverse of Cd. So the estimator of g is

Since the covariance matrix of ĝ is a constant time the identity matrix, the design d is balanced for the general combining abilities. Hence the proposed design d is variance balanced for general combining ability effects. We thus have the following theorem.
Theorem: For a positive odd prime or power of odd prime >3,
if there exits semi-balanced array (p (p-1)/2, p+1, p, 2), then there
always exists a V-B incomplete block design for CDC experiment
method (4).
Now substituting the estimate of τ and g from equations (6.3)
and (6.9) in equation (6.6), we obtain the estimator of s, namely

Since H11v = 0, H21v = 0, H1H2' = 0 , we haverank (H) = p−1 and rank (H2 ) = v − p .
It follows that g and s are represented by treatment contrasts
which carry p-1 and v-p degrees of freedom, respectively and that
the contrasts representing g are orthogonal to those contrasts
which represents. This means that the proposed design d allows
for gca and sca effects to be estimated independently of each other.
The sum of squares due to gca and sca for design d are given by
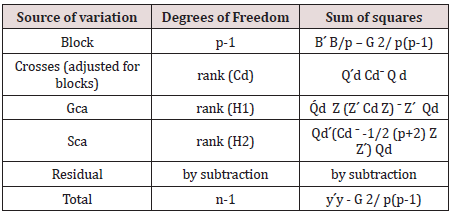
SS (gca) = Q'd Z(Z´ CdZ) ˉ Z´Qd (6.14)
SS (sca) = Qd '(Cdˉ −1 / ( p − 2)Z Z ') Qd (6.15)
The ANOVA is then given in Table 1.
Optimalityand Efficiency Factor
Since in design d every line is crossed with an equal number of different lines and the environmental design is equi-replicate, equiblock size (k< n) and binary, now using proposition of [14]to prove optimality of the proposed design, we have following theorem.
Theorem: Let be a block design for diallel cross, satisfying
(i) trace (Cd*) k-1b {2k (k-1-2x)+ px (x+1)} and
(ii) Cd*= (p -1)-1 k-1b {2k (k-1-2x)+ px (x+1)} (Ip-p-11p1'p ) is completely symmetric.
where = [2k/p],and for square matrix A, tr(A) stands for the
trace. Ip is an identity matrix of order p and 1p1′p is a p × p matrix
of all ones. Furthermore, using d *ε D ( p, b, k ) all elementary
contrasts among gca effects are estimated with variance  . Then d*
is universally optimal in D (p, b, k) and in particular minimizes
the average variance of the best linear unbiased estimators of all
elementary contrasts among the general combining ability effects.
Our proposed design d ɛ D (p, b, k) and has information matrix Cg
= (Z′CZ) and its trace is equal to 2(p-1(p-2) which can be verified by
equation (5.9) and it is equal to the trace given in theorem 6.1(i).
Hence design d is universally optimal.Suppose that instead of the
proposed design d, one adopts a randomized complete block design
with 2 blocks, each block having all p (p-1)/2 crosses. [2] on page
473 shows that the variance of any elementary contrast among the
gca effects is σ12 / (p-2), where σ12 is the per observation variance
in the case of a randomized block experiment. It is clear from (6.10)
that using design d each elementary contrast among gca effects is
estimated with variance σ2 / (p-2). . Hence the efficiency factor
of design d compared to a randomized block design under the
assumption of equal intra-block variances is given by
. Then d*
is universally optimal in D (p, b, k) and in particular minimizes
the average variance of the best linear unbiased estimators of all
elementary contrasts among the general combining ability effects.
Our proposed design d ɛ D (p, b, k) and has information matrix Cg
= (Z′CZ) and its trace is equal to 2(p-1(p-2) which can be verified by
equation (5.9) and it is equal to the trace given in theorem 6.1(i).
Hence design d is universally optimal.Suppose that instead of the
proposed design d, one adopts a randomized complete block design
with 2 blocks, each block having all p (p-1)/2 crosses. [2] on page
473 shows that the variance of any elementary contrast among the
gca effects is σ12 / (p-2), where σ12 is the per observation variance
in the case of a randomized block experiment. It is clear from (6.10)
that using design d each elementary contrast among gca effects is
estimated with variance σ2 / (p-2). . Hence the efficiency factor
of design d compared to a randomized block design under the
assumption of equal intra-block variances is given by
 (6.1)
(6.1)It implies that design d is as efficient as randomized block design.
Illustration
We show the essential steps of a CDC experiment method (4),
using an incomplete block design d. For this purpose, we take data
from an experiment on the number of tillers per plant in pearl
millet, reported by Sharma (1998) on page 220. The author used a
randomized complete block design with v = 36 as he considered p2
possible crosses including selling and reciprocal crosses, among p
= 6 inbred lines. For the purpose of illustration, we take the data of
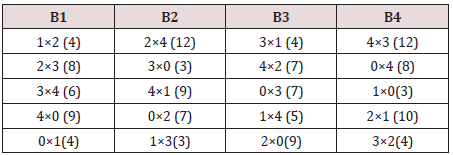
relevant crosses from this experiment. The layout and observations
in parentheses are given below [21]. There are10 crosses and each
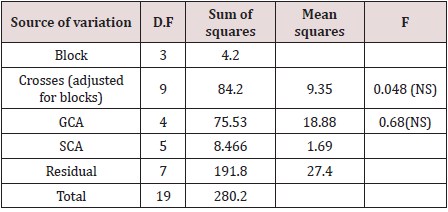
cross is replicated twice The ANOVA and the estimates of the gca
and sca effects are given in Tables 2, 3, & 4.
The following exhibits the vectors of block totals B, cross totals
T and adjusted block totals Q.
B = (31.00, 34.00, 32.00, 37.00) ́
T = (7, 16, 10, 17, 14, 7, 14, 12, 19, 18)
Q = (-6.60, 2.80, -3.20, 3.40, 0.40, -6.20, 0.80, -1.6, 5.80, 4.40)
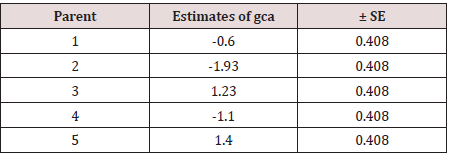
Table 4: Estimates of the general combining ability effects and their estimated error on number of tillers.
Result and Discussion
Variances: The simple ANOVA (Table2) tends to render
information about the basic nature of the parental material involved
in diallel crossing. Thus, significant variation among parents, among
crosses and among F1’s does indicate potential genetic differences
among the parents chosen and their potency. It is clear from Table
1that the effect of crosses is not significant.
b. Effects: (i) General combining ability (gca) effects: The
gca effects (gi) represent the additive nature of gene action. A high
general combiner (parent) is characterized by its better breeding
value when crossed with a number of parents. Depending upon
the character concerned, the nature and magnitude of gi are both
concerned. In the present example, none of the gi are significant
(Table 5, 6).
c. Specific combining ability (sca) effects: The sca effects
(sij) signify the role of non-additive gene action in character
expression. The highly specific combining ability effects leading to
highest performance of some specific cross combinations. In the
present example sca effects are not significant.
Table 5: Estimates of the specific combining ability effects and their estimated error on number of tillers.
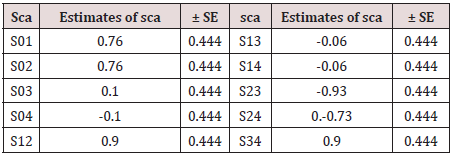
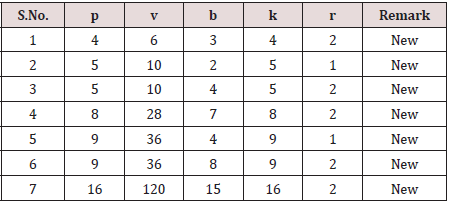
Table 6: Universally Optimal Block Designs for Diallel Cross method (4) experiments obtainable from semi-balanced arrays (p (p-1)/2, p, p, 2)..
Conclusion
Diallel crossing as mating designs are used to study the genetic properties of inbred lines in plant and animal breeding experiments. In the present article we have given some new incomplete block designs for Griffing’s CDC method (4) by using semi –balanced array (p (p-1), p, p, 2).
References
- Rao C R (1973) Some Combinatorial Problems of Arrays and Application to Design of Experiments. A survey to Design of experiments North Holland Chapter 29: 349-359.
- Griffing B (1956) Concept of General and Specific Combining ability in relation to diallel crossing systems. Aust J Biol Sci 9: 463-493.
- Gupta S, Kageyama S (1994) Optimal complete diallel crosses. Biometrika 81(2): 420-424.
- Dey A, Midha, Chand K (1996) Optimal designs for diallel crosses. Biometrika 83(2): 484-489.
- Mukerjee R (1997) Optimal partial diallel crosses. Biometrika 84(4): 937-946.
- Sharma R J (1998) Statistical and Biometrical Techniques in Plant Breeding New Age International Publication (p) Limited Publishers New Delhi India.
- Parsad R, Gupta V K, Srivastava R (1999) Optimal designs for diallel crosses. Jour Soc Stat Comp and Application 1: 35-52.
- Sharma M K (2004) Optimal complete diallel cross Advances in Mating Designs 15.
- Chai FS, Mukerjee R (1999) Optimal design for diallel crosses with specific combining abilities. Biometrika 86(2): 453-458.
- Choi K Chung, Chatterjee K, Das A, Gupta, S (2002) Optimality of Orthogonally blocked dialles with specfic combining abilities. Statistics Probability Letters 57: 145-150.
- Das A, Dey A, Dean A (1998) Optimal design for diallel cross experiments. Statist Prob Letters 36(4): 427-436.
- Kempthorne O (1956) The theory of diallel crosses. Genetics 41: 451-459
- Kiefer J (1975) Construction and optimality of generalized Youden designs. In a Survey of Statistical Design and Linear Models 333-353.
- Rao C R (1973) Linear Statistical Inference and its Applications. 2nd edition J Wiley and Sons New York.
- Singh M, Hinkelmann K (1998) Analysis of partial Diallel in Incomplete Block. Biometric journal 40(2): 165-181
- Sharma M K, Fanta Sileshi (2009) Incomplete Block Designs for CDC Method I and III. Metro 17(12):209-226.
- Raghavarao D (1971) Constructions and Combinatorial Problems in Design of Experiments. J Wiley and Sons New York.
- Dey A (1986) Theory of Block Designs. Wiley Eastern New Delhi.
- Kempthrone O, Curnow R N (1961) The partial diallel cross. Biometrics 17(2): 229-250
- Bose R C (1939) On the construction of balanced incomplete block designs. Ann Eugeneics 9: 353-399.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...