Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2644-1381
Review Article(ISSN: 2644-1381) 
Model Selection in Regression: Application to Tumours in Childhood Volume 1 - Issue 1
Annah Managa*
- Department of Statistics, University of South Africa, South Africa
Received: August 23, 2018; Published: September 10, 2018
*Corresponding author: Annah Managa, Department of Statistics, University of South Africa, South Africa
DOI: 10.32474/CTBB.2018.01.000101
Summary
We give a chronological review of the major model selection methods that have been proposed from circa 1960. These model selection procedures include Residual mean square error (MSE), coefficient of multiple determination (R2), adjusted coefficient of multiple determination (Adj R2), Estimate of Error Variance (S2), Stepwise methods, Mallow’s Cp, Akaike information criterion (AIC), Schwarz criterion (BIC). Some of these methods are applied to a problem of developing a model for predicting tumors in childhood using log-linear models. The theoretical review will discuss the problem of model selection in a general setting. The application will be applied to log-linear models in particular.
Keywords: MSE; R2; Adj R2; (S2); Stepwise methods; Cp; AIC; BIC
Introduction
Historical Development
The problem of model selection is at the core of progress in science. Over the decades, scientists have used various statistical tools to select among alternative models of data. A common challenge for the scientist is the selection of the best subset of predictor variables in terms of some specified criterion. Tobias Meyer (1750) established the two main methods, namely fitting linear estimation and Bayesian analysis by fitting models to observation. The 1900 to 1930’s saw a great development of regression and statistical ideas but were based on hand calculations. In 1951 Kullback and Leibler developed a measure of discrepancy from Information Theory, which forms the theoretical basis for criteria-based model selection. In the 1960’s computers enabled scientists to address the problem of model selection. Computer programmes were developed to compute all possible subsets for an example, Stepwise regression, Mallows Cp, AIC, TIC and BIC. During the 1970’s and 1980’s there was huge spate of proposals to deal with the model selection problem. Linhart and Zucchini (1986) provided a systematic development of frequentist criteria-based model selection methods for a variety of typical situations that arise in practice. These included the selection of univariate probability distributions, the regression setting, the analysis of variance and covariance, the analysis of contingency tables, and time series analysis. Bozdogan [1] gives an outstanding review to prove how AIC may be applied to compare models in a set of competing models and define a statistical model as a mathematical formulation that expresses the main features of the data in terms of probabilities. In the 1990’s Hastie and Tibsharini introduced generalized additive models. These models assume that the mean of the dependent variable depends on an additive predictor through a nonlinear link function. Generalized additive models permit the response probability distribution to be any member of the exponential family of distributions. They particularly suggested that, up to that date, model selection had largely been a theoretical exercise and those more practical examples were needed (see Hastie and Tibshirani, 1990).
Philosophical Perspective
The motivation for model selection is ultimately derived from the principle of parsimony [2]. Implicitly the principle of parsimony (or Occam’s Razor) has been the soul of model selection, to remove all that is unnecessary. To implement the parsimony principle, one has to quantify “parsimony” of a model relative to the available data. Parsimony lies between the evils of under over-fitting. Burnham and Anderson [3] define parsimony as “The concept that a model should be as simple as possible concerning the included variables, model structure, and number of parameters”. Parsimony is a desired characteristic of a model used for inference, and it is usually defined by a suitable trade-off between squared bias and variance of parameter estimators. According to Claeskens and Hjort [4], focused information criterion (FIC) is developed to select a set of variables which is best for a given focus. Foster and Stine [5] predict the onset of personal bankruptcy using least squares regression.
They use stepwise selection to find predictors of these from a mix of payment history, debt load, demographics, and their interactions by showing that three modifications turn stepwise regression into an effective methodology for predicting bankruptcy. Fresen provides an example to illustrate the inadequacy of AIC and BIC in choosing models for ordinal polychotomus regression. Initially, during the 60’s, 70’s and 80’s the problem of model selection was viewed as the choice of which variable to include in the data. However, nowadays model selection includes choosing the functional form of the predictor variables. For example, should one use a linear model, or a generalized additive model or even perhaps a kernel regression estimator to model the data? It should be noted that there is often no one best model, but that there may be various useful sets of variabsles (Cox and Snell, 1989). The purpose of this paper was to give a chronological review of some frequentist methods of model selection that have been proposed from circa 1960 and to apply these methods in a practical situation. This research is a response to Hastie and Tibsharani’s (1990) call for more examples.
Data and Assumptions
In this paper the procedures described here, will be applied to a data set collected at the Medical University of Southern Africa (Medunsa) in 2009. The data consist of all the tumours diagnosed in children and adolescents covering the period 2003 to 2008. The files of the Histopathology Department were reviewed and all the tumours occurring during the first two decades of a patient’s life were identified. The following variables were noted: age, sex, site. The binary response variable indicated the presence of either malignant (0) or benign (1) tumours. In our setting, the problem of model selection is not concerned with which number of predictor variables to include in the model but rather, which functional form should be used to model the probability of a malignant tumour as a function of age. For binary data it is usual to model the logit of a probability (the logit of the probability is the logarithm of the odds), rather than the probability itself. Our question was then to select a functional form for the logit on the bases of a model selection criterion such as Akaike information criterion (AIC) or Schwarz criterion (BIC).
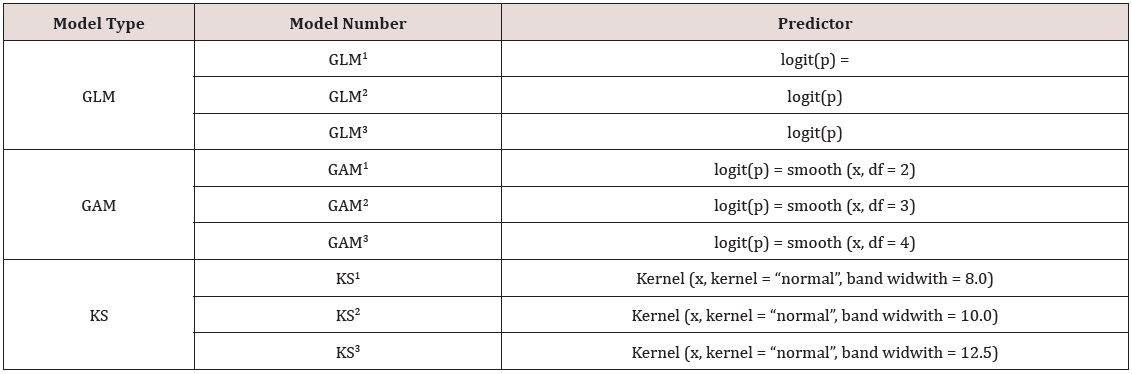
We considered various estimators for the logit, namely using linear or quadratic predictors, or additive with 2, 3, and 4 degrees of freedom. As an alternation, the probabilities were modeled using Kernel estimator with Gaussian Kernel for various bandwidths, namely 8.0, 10.0 and 12.5. The model selection criterion that was used are AIC and BIC. Based on the above approach, recommendations will be made as to which criteria are most suitable for selecting model selection. The outline of this paper is as follows. In Section 2, we provide a brief review of the related literature. Section 3 presents technical details of some of the major model selection criteria. Some model selection methods which were applied to a data set will be discussed in Section 4. Finally, Section 5 will provide conclusions and recommendations.
Literature Review
The problem of determining the best subset of independent variables in regression has long been of interest to applied statisticians, and it continues to receive considerable attention in statistical literature [6-9]. The focus began with the linear model in the 1960`s, when the first wave of important developments occurred and computing was expensive and time consuming. There are several papers that can help us to understand the state-of-the-art in subset selection as it developed over the last few decades. Gorman and Toman [10] proposed a procedure based on a fractional factorial scheme in an effort to identify the better models with a moderate amount of computation and using Mallows as a criterion. Aitkin [11] discussed stepwise procedures for the addition or elimination of variables in multiple regression, which by that time were very commonly used. Akaike [12] adopted the Kullback-Leibler definition of information, as a measure of discrepancy, or asymmetrical distance, between a “true” model and a proposed model, indexed on parameter vector.
A popular alternative to AIC presented by Schwarz [13] that does incorporate sample size is BIC. Extending Akaike’s original work, Sugiura (1978) proposed AICc, a corrected version of AIC justified in the context of linear regression with normal errors. The development of AICc was motivated by the need to adjust for AIC’s propensity to favour high-dimensional models when the sample size is small relative to the maximum order of the models in the candidate class. The early work of Hocking [14] provides a detailed overview of the field until the mid-70’s. The literature, and Hocking’s review, focuses largely on (i) computational methods for finding best-fitting subsets, usually in the least – squares sense, (ii) mean squares errors of prediction (MSEP) and stopping rules. Thomson [15] also discussed three model selection criteria in the multiple regression set-up and established the Bayesian structure for the prediction problem of multiple regression.
Some of the reasons for using only a subset of the available predictor variables have been reviewed by Miller [16]. Miller [17] described the problem of subset selection as the abundance of advice on how to perform the mechanics of choosing a model, much of which is quite contradictory. Myung [18] described the problem of subset selection as choosing simplest models which fit the data. He emphasized that a model should be selected based on its generalizability, rather than its goodness of fit. According to Forster [9], standard methods of model selection, like classical hypothesis testing, maximum likelihood, Bayes method, Minimum description length, cross-validation and Akaike’s information criterion are able to compensate for the errors in the estimation of model parameters. Busemeyer and Yi-Min Wang [19] formalized a generalization criterion method for model comparison. Bozdogan [20] presented some recent developments on a new entropic or information complexity (ICOMP) criterion for model selection. Its rationale as a model selection criterion is that it combines a badness-of-fit term (such as minus twice the maximum log likelihood) with a measure of complexity of a model differently than AIC, or its variants, by taking into account the interdependencies of the parameter estimates as well as the dependencies of the model residuals. Browne [21] gives a review of cross-validation methods and the original application in multiple regression that was considered first. Kim and Cavanaugh [22] looked at modified versions of the AIC (the “corrected” AIC- and the “improved” AICM) and the KIC (the “corrected” KIC- and the “improved” KICM) in the nonlinear regression framework. Hafidi and Mkhadri derived a different version of the “corrected” KIC ÐKIC-) and compared it to the AIC- derived by Hurvich and Tsai. Abraham [23] looked at model selection methods in the linear mixed model for longitudinal data and concluded that AIC and BIC are more sensitive to increases in variability of the data as
opposed to the KIC
Frequentist Model Selection Criteria
Tools for Model Selection in Regression
Model selection criteria refer to a set of exploratory tools for improving regression models. Each model selection tool involves selecting a subset of possible predictor variables that still account well for the variation in the regression model’s observation variable. These tools are often helpful for problems in which one wants the simplest possible explanation for variation in the observation variable or wants to maximize the chance of obtaining good parameter values for regression model. In this section we shall describe several procedures that have been proposed for the criterion measure, which summarizes the model; These include coefficient of multiple determination (R2), Adjusted-R2 and residual mean square error (MSE), stepwise methods, Mallow’s Cp, Akaike information Criteria (AIC) and Schwarz criterion (BIC). The focus will be on AIC and BIC [24-28].
R2
Is the coefficient of multiple determination and the method to find subsets of independent variables that best predict a dependent variable by linear regression. The method always identifies the best model as the one with the largest for each number of variables considered.
This is defined as
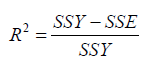
Where SSE (the sum of squares of residuals) and SSY
Adjusted R - square (adj-R2)
Since the number of parameters in the regression model is not taken into account by R2, as R2 is monotonic increases, the adjusted coefficient of multiple determination (Adj - R2) has been suggested as an alternative criterion. The Adj - R2 method is similar to the method and it finds the best models with the highest Adj- R2 within the range of sizes.
To determine this, we may calculate the adjusted Rsquare. This is defined as

where MSY = SSY /( N −1) and MSE = SSE /(n − k) .
Mean Square Error MSE
The mean square error measures the variability of the observed points around the estimated regression line, and as such is an estimate of the error variance σ 2 . When using as model selection tools, one would calculate the possible subset of the predictor variables and then select the subset corresponding to the smallest value of MSE to be included to the final model.
It is defined as
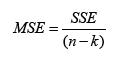
where SSE is again merely the sum squared error terms and does not take account how many observations. The smaller the value of MSE, the closer the predicted values come to the real value of respond variables.
Mallows Statistics Cp
A measure that is quite widely used in model selection is the Cp criterion measure, originally proposed by C.L. Mallows (1973). It has the form:
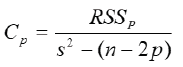
where RSSp residual sum of squares from a model containing p parameters, p is the number of parameters in the model including 0 β, s2 is the residual mean square from the largest equation postulated containing all the X's, and presumed to be a reliable unbiased estimate of the error variance σ2.
R.W. Kennard (1971) has pointed out that Cp is closely related to the adjusted Rp2 and Rp2 statistic. Let us consider the relationship between adj- Rp2 or Rp2 & Cp.
Rp2 can be written as
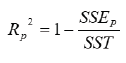
where SSEp being the error of squares and SST is the total sum of squares.
The adjusted coefficient of multiple determination (Adj - Rp2),
may also be considered as:
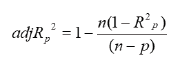
Rp2 and adjRp2 is used for model containing only p of the K predictor variables. When the full model is used (all k predictor variables included) the following notation is used:
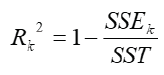
and the estimate of the error variance is then given as:
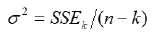
From equation (i) making SSEp the subject of the formula. It follows that
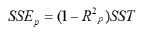
Substitute this into Cp
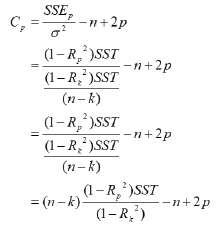
It is easily seen that Cp can be written as a function of the multiple correlation coefficient. Making (1 − Rp2) the subject of the formula from equation (3.7). It follows that in the relationship between Cp and adjR(p)2 we have
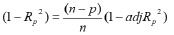
Then from
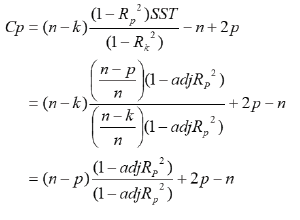
It is clear that there is a relationship between the adj-Rp2 or Rp2 and Cp statistics. In fact in both cases for each P the minimum Cp and the maximum adj-Rp2 or Rp2 occur for the same set of variables, although the P value of finally chosen may of course differ. The factor (n − k) in the first equation may cause decreases in minimum Cp values as P increases although Rp2 is only slowly increasing. Several authors have suggested using Cp as a criterion for choosing a model. We look for model with a small Cp and P preferably we look for a Cp close to P which means a small bias.
Forward Selection
In the forward selection procedure the analysis begins with no explanatory (independent) variables in the regression model. For each variable, a statistic called an F-statistic (F -to-enter) is calculated; this F-statistic reflects the amount of the variable’s contribution to explaining the behaviour of the outcome (dependent) variable. The variable with the highest value of the F - statistic (F-to-enter) is considered for entry into the model. If the F -statistic is significant then that variable is added to the model. If -statistic (F -to-enter) is greater than 10 or more, then explonatory variables are added to form a new current model. The forward selection procedures are repeated until no additional explanatory variables can be added [29-32].
Backward Elimination
The backward elimination method begins with the largest regression, using all possible explanatory variables and subsequently reduces the number of variables in the equation until is reached in the equation to use. For each variable, a statistic called an F -statistic (F-to-remove) is calculated. The variable with the lowest value of the F-statistic (F-to-remove) is considered for removal from the model. If the -statistic is not significant then that variable is removed from the model; if the F-statistic (F -to-remove) is 10 or less, then explanatory variables are removed to arrive at a new current model. The backward selection procedures are repeated until none of the remaining explanatory variables can be removed [33-39].
Stepwise Regression
Stepwise Regression is a combination of forward selection and backward elimination. In stepwise selection which can start with a full model, with the model containing no predictors, or with a model containing some forced variables, variables which have been eliminated can again be considered for inclusion, and variables already included in the model can be eliminated. It is important that the F-statistic (F-to-remove) is defined to be greater than the F-statistic (F-to-enter), otherwise the algorithm could enter and delete the same variable at consecutive steps. Variables can be forced to remain in the model and only the other variables are considered for elimination or inclusion.
Akaike Information Criterion (AIC)
Akaike (1973) adopted the Kullback-Leibler definition of information I(f;g), as a measure of discrepancy, or asymmetrical distance, between a “true” model f and a proposed model g, indexed on parameter vector Θ . Based on large-sample theory, Akaike derived an estimator for I(f;g) of the general form:
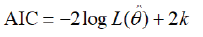
where the first term tends to decrease as more parameters are added to the approximating family g(y/Θ) The second term may be viewed as a penalty for over-parameterization.
Akaike Information Criterion (AIC)
Bayesian Information Criterion (BIC) Bayesian information criterion (BIC) was introduced by Schwartz in 1978. BIC is asymptotically consistent as a selection criterion. That means, given a family of models including the true model, the probability that BIC will select the correct one approaches one as the sample size becomes large. AIC does not have the above property. Instead, it tends to choose more complex models as for small or moderate samples; BIC often chooses models that are too simple, because of its heavy penalty on complexity.
A model, which maximizes BIC is considered to be the most appropriate model.
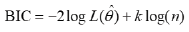
Where L is the maximum log likelihood, k is the number of free parameters and n is the number of independent (scalar) observation that contributes to likelihood. Model selection here is carried out by trading off lack of fit against complexity. A complex model with many parameters, having large value in the complexity term, will not be selected unless its fit is good enough to justify the extra complexity. The number of parameters is the only dimension of complexity that this method considers than AIC, BIC always provides a model with a number of parameters no greater than that chosen by AIC.
Methods
In this paper the data were partitioned into 13 sites and models fitted independently to each site. This was partially motivated during a personal discussion with Sir David Cox of the University of Oxford, who suggested that the tumours at different sites may in fact be different diseases, and therefore, may require different models for the logit of the probabilities of malignant tumours. The response variable indicated the presence of either malignant or benign tumours and is therefore a binary response. The task was now to model the probability of a malignant tumour in terms of patient age. The modern regression theory indicates that the logit of these probabilities, rather than the probabilities themselves, should be modelled either by a General Linear Model (GLM), Generalized Additive Model (GAM) or a Kernel Smooth.
At each of the 13 sites, the logit of the probabilities was modelled by increasingly flexible predictors namely: A GLM using linear or quadratic predictors, a GAM with 2, 3, and 4 degrees of freedom and a Gaussian Kernel smooth using various bandwidths, namely 8.0, 10.0 and 12.5. These are summarised in Table 1. In order to select which of the above model predictor combinations was the best at each site, we applied the model selection criteria AIC, BIC and AICc. All models were fitted using S-plus 4.0 for the purpose of assessing the models in this study. The routines for computing AIC, BIC and AICc in S-plus are given in Appendix 1 to 13. The model selection criteria, AIC, BIC and AICc were computed for each of the models described in Table 1 at each site. The model with the smallest value of AIC, BIC and AICc was then selected as the best model at a particular site. Because the Kernel smooth is a non-parametric regression without distributional assumption, it does not have a likelihood function associated with it. Because of this, the model selection criteria AIC, BIC and AICc, all of which require a likelihood, cannot be computed. We have used Kernel estimators as a non- parametric check on the best model selected from the GLM’s and GAM’s.
Results
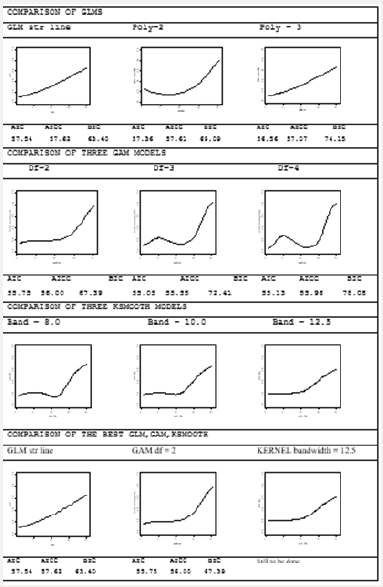
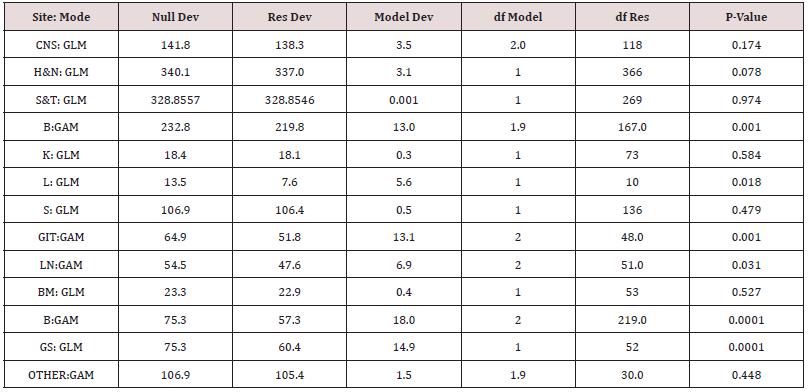
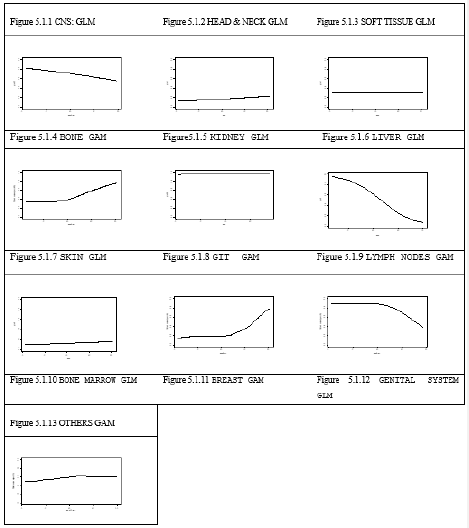
This section provides a detailed analysis of site 8 (Figure1) and a summary of the best models that were fitted at each of the best sites. This was done through presentation and discussion of the fitted models using graphs (Figure 2) followed by the analysis of deviance for each of thse fitted models as shown in Table 2. Detailed statistics for the other sites are given in Appendix 1.
Figure 2: Graphs of estimated probabilities of malignant tumours for the best model at each of the13 sites using either a GLM or a GAM.
Detailed Analysis of Site 8 (Genital Internal Track)
Consider the first row of model in Figure 2 which represents the GLM using respectively a linear, quadratic and cubic predictor i.e
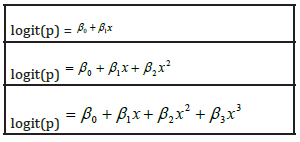
For these three models, using AIC, BIC and AICc as the model selection criteria, the GAM with 2 degrees of freedom was the selected model. In Figure 2 the first row provides a comparison of the GLM’s using a linear, quadratic and cubic predictor. Both the linear and cubic predictor appears to give similar reasonable results. The quadratic predictor, however, seems to have too much forced curvature in the left-hand corner which appears to be contrary to medical experience. The second row provides a comparison of GAM’s using 2, 3, and 4 degrees of freedom respectively. The models with 3 and 4 degrees of freedom appear to have too much force curvature. The Gaussian Kernel smooth for bandwidth of 8.0 and 10.0 shows jubias curve that cannot reflect the probabilities observed in real life. The third row provides a comparison of the three final curves selected as the best fitted model from the GLM, the GAM and the Kernel Smooth. Based on the AIC, BIC and AICc criteria we have selected the GAM with 2 degrees of freedom values that are listed below the graph. It can be seen from the graph that although this has the minimum value of AIC, it is highly constrained by linearity of the predictor. The Kernel Smooth, however, is much more flexible and therefore more able to follow the data. The Kernel Smooth also seems to indicate that the logit may not be linear.
Discussion
Central Nervous System (Figure 2). The graph conveys that the probability of a malignant tumour starts from 80% at birth and decreases to 50% at age 20. The majority of tumours are malignant primitive neuroectodermal tumours and there are few benign tumours. As the children become older, the increase in astroeytic tumours remain few.ss The model deviance is 3.5 on 2.0 degree of freedom with the p=0.174 Therefore we concluded that the model is not significant for the deviance. Head and Neck (Figure 2). It starts from 10% for infants and increases to 20% for teens. The majority of these tumours are benign haemangiomas and lymphangionias.
Very few malignant tumours occur in this area. The model deviance of 3.1 on 1 degree of freedom with a p= 0.078 which is not significant (Table 2). Therefore, the model is not significant for reducing the deviance in head and neck. Soft tissue (Figure 2) There is no change of the probability of a malignant tumour from infants to late teens. The majority of these tumours are benign, which it remains constant at 30%. Soft tissue sarcoma is rare. The commonest tumours are lymphomas and haemangiomas. The model is not significantly different from the null model of constant probability: The model deviance is 0.001 on 1 degree of freedom with a p= 0.974. Therefore, we concluded that the model is not significant for the deviance. Bone (Figure 2) The probability of a malignant tumour starts from 35% in early childhood and remains constant until age 10 and then rises steeply during the teens to 80% at age 20. Bone tumours are rare in infancy.
The sudden rise of the curve is caused by osteosarcoma which is common between the ages of 10 to 20 years. The model deviance is 13.0 on 1.9 degrees of freedom with a p= 0.001. Therefore, we concluded that the model explains a significant portion of the deviance. Kidney (Figure 2) There is a constant probability of malignant tumours close to 100% over all ages from early childhood to age 20. The malignant tumour are nephroblastomas. A few cases of congenital neuroblastic nephroma were seen in malignant tumour. The model is not significantly different from the null model of constant probability: model deviance of 0.3 on 1 degree of freedom with a p=0.584. Therefore, we concluded that the model is not significant for the deviance.
Liver (Figure 2) The probability curve starts from 95% for infants and steadily declines to 10% during the teen’s years. The malignant tumours are Hepatoblast, which is common before two years. This should explain the sudden decline of the curve because malignant tumours are indeed very high. The model deviance is 5.6 on 1 degree of freedom with a p= 0.018. Therefore, we concluded that the model explained a significant portion of deviance. Skin (Figure 2) There is a constant probability of malignant tumours close to 10% from early childhood to age 10 and this probability steadily rises to 20% during teen years. A few malignant tumours are present. The probability of contracting a malignant tumour such as Kaporis sarcoma is rare in children. The model deviance is 0.5 on 1 degree of freedom with a p= 0.479. Therefore, we concluded that the model does not explain a significant portion of deviance. Genital Internal Track (Figure 2) The graph conveys that the probability of a malignant tumour starts from 15% for infants and remains constant until age 13 and then rises steeply during the teens to 80% at age 20. This is consistent with the experience in medical practice that the probability of contracting a malignant tumour, at a very young age in the genital internal track is indeed very low and that there is a sudden rise of malignant tumours around the age of 13.
The sudden rise in the 2nd decade is caused by lymphomas. The model is strongly significant: The model deviance is 13.1 on 2 degrees of freedom with a p= 0.001. Therefore, we concluded that the model explains a significant portion of deviance. Lymph Nodes (Figure2) The probability curve starts from infants at 90% and remains constant until age 12 and then decreases during the teens to 40% at age 20. Tumours at a very young age are lymph nodes which are very high and there is a decrease of the probability curve at the age of 13. The commonest tumours were lymphomas. The model deviance is 6.9 on 2 degrees of freedom with a p=0.031 Therefore we concluded that the model explains a significant portion of deviance. Bone Marrow (Figure 2) There is a constant probability of malignant tumours close to 100% from early childhood to age 20 years of age. This resonates with the experience in medical practice that the probability of contracting malignant tumours is lymphomas and leukaemias that are found in malignant tumours. The model is not significantly different from the null model of constant probability. The model deviance is 0.4 on 1 degree of freedom with a p= 0.527. Therefore, we concluded that the model is not significant. Breast (Figure 2) The probability curve starts from 90% at birth and steadily declines from malignant to benign tumours and remains constant at 10% to late teens. There was only one malignant tumour at four years. This concurs with the experience in medical practice that the probability of contracting a malignant tumour increases after puberty and it is caused by fibroadenomas. The model is strongly significant: The model deviance is 18.0 on 2 degrees of freedom with a p= 0.0001. Therefore, we concluded that the model explains a signify, can’t portion of deviance.
Genital System (Figure 2) There is a constant probability of malignant tumours close to 40% from early childhood to age 10 and slightly decreases to 2% during teen years. A few malignant tumours are present. This is in line with the experience found in medical practice that the probability of contracting a malignant tumour is benign teratomas. The model is not significant: The model deviance is 14.9 on 1 degree of freedom with a p= 0.0001. Therefore, we concluded that the model is not significant for the deviance in genital system. Others (Figure 2) The graph indicates that the probability of a malignant tumour starts from 45% for infants and remains constant until age 13 and then rises steeply during the teens to 50% until age 20. Malignant tumour for this group of patients constitutes all those sites which did not have enough cases. This should include sites where childhood malignamies which are common, and they are rare. The model deviance is 1.5 on 1.9 degrees of freedom with a p-value of 0.448 (Table 2) Therefore, we concluded that the model is not significant for the deviance.
Conclusion and Recommendation
The problem of model selection occurs almost everywhere in statistics and we are facing more complicated data sets in the study of complex diseases. Tools that are more appropriate to the problem, more flexible to use, providing a better description, should be adopted. Model selection by AIC and BIC is one of these tools. We fitted a General Linear Model, Generalized Additive Model or Kernel Smooth using AIC and BIC model selections to the binary response to model the probability of a malignant tumour in terms of patient age. The probability of contracting a malignant tumour is consistent with the experience in medical practice and is an example of how model selections should be applied in practice. The probability distribution of the response variable was specified, and in this respect, a GAM is parametric.
In this sense they are more aptly named semi-parametric models. A crucial step in applying GAMs is to select the appropriate level of the ‘‘smoother’’ for a predictor. This is best achieved by specifying the level of smoothing using the concept of effective degrees of freedom. However, it is clear that much work still has to be done, because we have found that the Kernel smooth is a non-parametric regression which is therefore does not have likelihood function associated with it. Because of this the model selection criteria AIC and BIC, both of which require a likelihood, cannot be computed. We have used Kernel estimators as a non- parametric check on the best model selected from the GLM’s and GAM’s.
References
- Bozdogan H (1987) Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Pschometrika 52(3): 345-370.
- Forster MR (2000) Key concepts in model selection: Performance and generalizability. Journal of Mathematical Psychology 44(1): 205-231.
- Burnham KP, Anderson DR (2002) Model Selection and Inference: A Practical Information-Theoretic Approach. New York: Springer-Verlag, USA.
- Gerda C, Nils LH (2003) The Focused Information Criterion. Journal of the American Statistical Association 98(464): 900-916.
- Dean P Foster, Robert A Stine (2004) Variable Selection in Data Mining: Building a Predictive Model for Bankruptcy. Journal of the American Statistical Association 466(99): 303-313.
- Hocking RR (1976) The analysis and selection of variables in linear regression. Biometrika 32(1): 1-49.
- Broersen PMT (1986) Subset regression with stepwise direct search. Journal of Applied Statistics 35: 168-177.
- McQuarrie ADR, Tsai CL (1998) Regression and Time Series Model Selection. Singapore World Scientific.
- Zucchini W (2000) An introduction to model selection. Journal of Mathematical Psychology 44: 41-61.
- Gorman JW, Toman RJ (1966) Selection of variables for fitting equations. Technometrics 8(1): 27-51.
- Aitkin MA (1974) Simultaneous Inference and the Choice of Variable Subset in Multiple Regressions. Technometrics 16(2): 221-227.
- Akaike H (1973) Information Theory and an Extension of the Maximum Likelihood Principle. In BN Petrov and F Csake (Eds.); Second International Symposium on Information Theory. Budapest: Akademiai Kiado pp: 267-281.
- Schwarz G (1978) Estimating the dimension of a model. Annals of Statistics 6(2): 461-464.
- Hocking RR (1976) The analysis and selection of variables in linear regression. Biometrika 32(1): 1-49.
- Thompson ML (1978) Selection of variable in multiple regressions Part 1. A Review and Evaluation International statistical review 46(1): 1-19.
- Miller AJ (1984) Selection of subsets of regression variables. Journal of the Royal Statiatics Society 147(3): 389-425.
- Miller A (1990) Model section in Regression. London Chapman and Hall, UK.
- Myung IJ (2000) The importance of complexity in model selection. Journal of Mathematical Psychology 44(1): 190-204.
- Busemeyer JR, Yi-Min Wang (2000) Model comparisons and model selection based on generalization test methodology. Journal of the Mathematical Psychology 44: 171-189.
- Bozdogan H (2000) Akaike’s information criterion and recent development in information complexity. Journal of Mathematical Psychology 44: 345-370.
- Browne MW (2000) Alternative ways of assessing model fit. Sociological methods and research 21: 230-258.
- Kim H, Cavanaugh JE (2005) Model selection criteria based on Kullback: Information measures for nonlinear regression. Journal of Statistical Planning and Inference 134(2): 332-349.
- Abraham A (2008) Model selection methods in the linear mixed model for longitudinal data unpublished PhD thesis, Chapel Hill University, USA.
- Akaike H (1974) A new look at the statistical model Identification. IEEE Transactions on automatic control AC 19(3): 716-723.
- Atkinson AC (1980) A note on generalized information criterion for choice of a model. Biometrics 67(2): 413-418.
- Bai ZD, Krishnaiah PR, Sambamoorthi N, Zhao LC (1992) Model selection for log-linear model. Sankhya B 54: 200-219.
- Cantoni E, Flemming JM, Ronchetti E (2005) Variable selection for marginal longitudinal generalized linear models. Biometrics 61(2): 507- 514.
- Draper NR, Smith H (1998) Applied Regression Analysis (2nd edn.); John Wiley and Sons New York, USA.
- Fujikoshi Y, Sotoh K (1997) Modified AIC and Mallows Cp in multivariate Linear Regression. Biometrika 84(3): 707-716.
- George ET (2000) The model section problem. Austin University of Texas press, USA.
- Hao HZ, Wahba G, Yin Lin, Meta V Ferris M, Klein R, et al. (2004) Variable Selection and Model Building via Likelihood Basis Pursuit. Journal of the American Statistical Association 99(467): 659-672.
- Hawkins DM (1973) On the investigation of alternative regression by principal component analysis. Applied Statistics 22(3): 275-286.
- Hurvich CM, Tsai CL (1991) Bias of the corrected AIC criterion for underfitted regression and time series models. Biometrika 78(3): 499- 509.
- Lindley DV (1968) The choice of variable in multiple regression. Journal of the Royal Statistical Society: Serial B 30: 31-66.
- Mallows CL (1973) Some comment on Cp. Techno metrics 15(4): 661- 676.
- McQuarrie ADR, Tsai CL (1998) Regression and Time Series Model Selection. Singapore World Scientific.
- Stone M (1977) An asymptotic equivalence of choice of model by crossvalidation and Akaike criterion. Journal of the Royal Statiatics Society B 39(1): 44-47.
- Sparks RS, Zucchini W, Coutsourides D (1985) On Variable Selection in Multivariate Regression. Commun Statistis OETheor Meth 14: 1569- 1587.
- Yi Min Wang (2002) Comparison and model selection based on Generalization criterion methodology. Journal of Mathematical Psychology 44(1): 171-189.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...