Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2644-1381
Research Article(ISSN: 2644-1381) 
Balanced Designs for Partial Double Cross Volume 3 - Issue 4
Mahendra Kumar Sharma* and Mohammed Omer Ibrahim
- Addis Ababa University, Ethiopia
Received: December 03, 2021 Published: January 6, 2022
*Corresponding author: Mahendra Kumar Sharma, Addis Ababa University, Ethiopia
DOI: 10.32474/CTBB.2022.03.000166
Abstract
Hinkelmann [1] constructed optimal balanced tetra partial cross i.e. optimal balanced partial double cross using balanced incomplete block designs and partially balanced incomplete block designs. In the present article we are presenting method of construction of three series of balanced partial double cross designs using nested balanced incomplete block designs in one way set up, when p is odd. Our proposed designs for partial double cross are new. AMS classification: 62 k 05.
Keywords: Nested Balanced Incomplete Block Design; Complete diallel Cross; Balanced Partial Double Cross; Block Design; Optimality
Introduction
Mating designs involving multi–allele cross m (≥ 2) ines play very important role to study the genetic properties of a set of inbred lines in plant breeding experiments. A most common type of mating design in genetics is the diallel cross which consist of v = p ( p −1) / 2crosses of p inbred lines such that the crosses of the type (i × j ) = ( j × i ) for i, j = 1, 2,..., p . This type of mating design is called complete diallel cross (CDC) method 4 of Griffing (1956). The concept of CDC can be easily extended to double cross designs. A double cross mating design is obtained by crossing two unrelated F1 hybrids symbolized as (i × j) and (k × l), where i ≠ j ≠ k ≠ l, are 4 parents and (i × j) and (k × l), are two F1’s{see Singh et al.2012}. Omitting reciprocal crosses, there exist
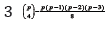
Let nc denote the total number of crosses involved in a balanced partial double cross design. Generally double cross experiments are conducted using a Completely Randomized Design (CRD) or a Randomized Complete Block (RCB) design involving some or all of the nc crosses as treatments. The number of crosses in such a mating design increases rapidly with increase in the number of lines. It leads to an overall inefficient experiment. It is for this reason that the use of incomplete block design as environment design is needed for double cross experiments [2]. Constructed optimal block designs for partial double cross experiment by using balanced incomplete block designs and nested balanced incomplete block designs [3]. Sharma and [4] constructed double cross designs for even and odd value of p by using initial block of unreduced balanced incomplete block designs given [1] and initial block of row-column designs given by [5], respectively. In this paper we are using initial blocks of nested balanced incomplete block designs [6] [7] for the construction of three series of balanced partial double cross designs in one way set up, when p is odd. The parameters of our proposed balanced partial double cross designs are different from [2] designs. In our proposed designs every cross is replicated equal number of times in a design and every line occurs in single cross with every line. We have considered the model that includes the gca effects, apart from block effects, but no specific combining ability effects.
Some Definitions:
Before we describe the constructions, it might be appropriate to recall some definitions.
Definition: The double cross has been defined [8] as a cross between two unrelated F1 hybrids, say denoted by (i × j)and (k × l ) where i ≠ j ≠ k ≠ l ≠ i, are denoting the grandparents and no two of them are same. Ignoring reciprocal crosses, with p grandparents, there will be
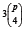
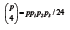
Definition: According to [9], a set of mating is said to be partial double crosses, if the following conditions are satisfied:
a) Every line occurs exactly r times in the set,
b) Every four-way cross occurs either once or not at all.
Definition: According to [9], a set of mating is said to be partial double crosses in the strict sense, if it satisfies the condition of Definition 2.2 and
a) Every single cross occurs once or not at all in the set.
Definition: According to [9], a partial double cross is said to be balanced partial double crosses, if every line occurs equally often with every other line in the same single cross.
Definition: According to [10], an arrangement of p treatments each replicated r* times in two systems of blocks is said to be a nested balanced incomplete design (NBIBD) with parameters
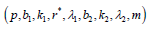
a) The second system is nested within the first, with each block from the first system, called hence forth as’ block’ containing exactly m blocks from the second system, called hereafter as sub blocks.
b) Ignoring the second system leaves a balanced incomplete block design with parameters
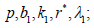
c) Ignoring the first system leaves a balanced incomplete block design with parameters
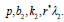
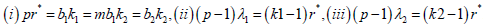
Definition: A design d* ɛ D (p, b, k) is said to be A-optimal if and only if
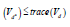
Method of Construction
Consider a nested balanced incomplete block design d obtained by developing t1 initial blocks mod (p), each sub-block is divided into t2 sub-blocks. The parameters of such a NBIB design are
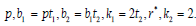
For such a design
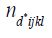
The information matrix for designd1 is given below.
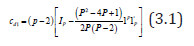
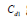
trace of
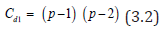
Using d1 each elementary contrast among line effects is estimated with a variance
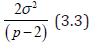
Now we give the method of construction of three series of balanced partial double cross designs using NBIB designs [11].
Series: Let p = 4t +1,t ≥1 be a prime or a prime power and x be a primitive element of the GF (p). Consider the following t initial blocks.
{(xi , xi+2t ),(xi+t , xi+3t )} ,i = 0,1, 2,...t −1.
As shown [11], these initial blocks, when developed in the sense of Bose (1939), give rise to a nested balanced incomplete block design with parameters.
v = p = 4t +1,b1 = t (4t +1), r = 4t, k1 = 4,λ1 = 3,b2 = 2t (4t +1)k2 = 2,λ 2 =1
Arrange the following m initial blocks into single block
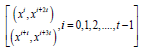
By making pair of crosses in a single block and developing mod (p), we get balanced partial double
cross design with parameters
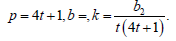
Remark: For construction of balanced partial double cross design it is necessary that the block size of a single block must be an even number i.e. t must be a multiple of 2. The procedure to construct the above designs, has been explained by the following illustrative examples.
Example: If we let t = 2, we get the following two blocks.
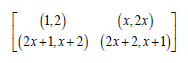
We can now write both blocks in a single block as given below.
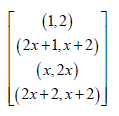
where is a primitive element of GF(32). Now cross the elements of the individual block and put these crosses in a single block. Adding successively the non-zero elements of GF (32) to the contents of the single block, we obtain block design for partial double cross experiment with parameters p = 9,b = 9, k = 2. The design is exhibited below, where the lines have been relabelled 1-9, using the correspondence 0→1,1→2, 2→3, x→4, x +1→5, x + 2→6, 2x +1→8, 2x + 2→9 :
Partial Double Cross Block Design
B1 B2 B3 B4 B5 B6
(2×3)×(6×8) (1×3)×(4×9) ( 1 × 2 ) × ( 5 × 7 )
(5×6)×(2×9) (4×6)×(3×7) (4×5)×(1×8)
(4×7)×(5×9) (5×8)×(6×7) (6×9)×(4×8) (1×7)×(3×8)
(2×8)×(1×9) (3×9)×(2×7)
B7 B8 B9
(8×9) × (3×5) (7×9) × (1×6) (7×8) × (2×4)
(1×4) × (2×6) (2×5) × (3×4) (3×6) × (1×5)
According to [2] the above design is balanced and is of minimal size, hence optimal.
Series: Let p = 6t +1,t ≥1 be a prime or a prime power and x be a primitive element of the Galois field of order p. Consider the set of initial blocks
{(xi , xi+3t ),(xi+t , xi+4t ),(xi+2t , xi+5t )},i = 0,1, 2,...t −1.
Dey, et al. (1986) showed when these initial blocks developed over mod (p), give a solution of a nested incomplete block design with parameters
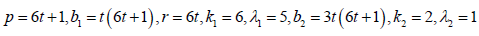
We can then arrange the above initial blocks into a single block as given below
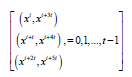
Example 2: Let t = 2. Then we get the following two initial blocks
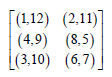
We can arrange these two blocks in a single block as given below.
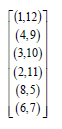
Now performing crosses in pairs and developing these crosses over mod (p), we obtain A- optimal block
design for partial double cross with parameters
p = 13,b = 13and k = 3.
Series: Let p = 2t +1,t ≥ 2 be a prime or a prime power and consider the following m blocks
(0, 2t),(1, 2t −1),(2, 2t −1).....(t −1,t +1)mod (2t +1)
Example 3: If we let t = 4, then the single block will be as given below.
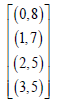
Now applying the procedure given above in example 1, we can obtain an A-optimal block design for double cross experiment with parameters
p = 9,b = 9, k = 2
Note 2: The t blocks given in series 3 form a nested balanced incomplete block design with parameters
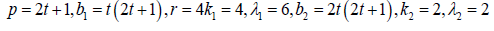
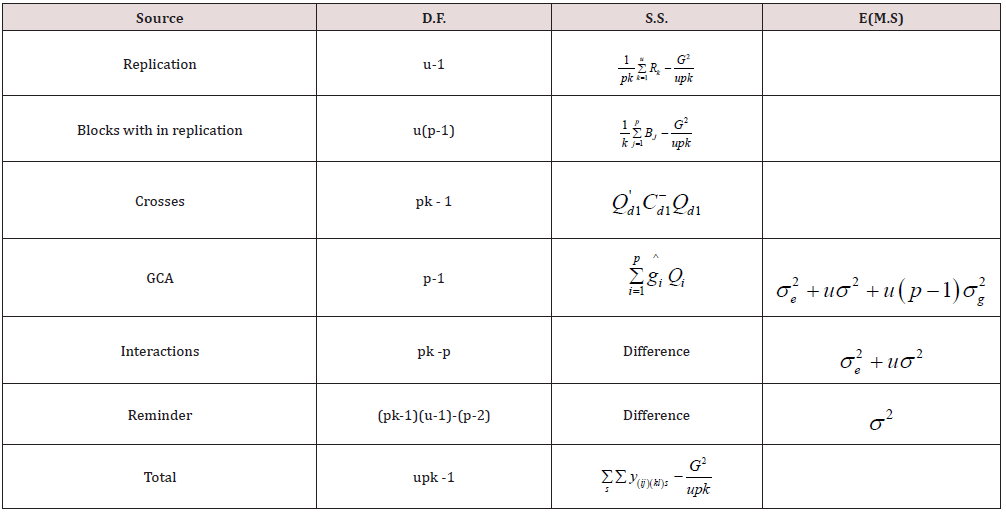
Analysis of Bpdc Design
Following [9] we can assume the following reduced model for proposed incomplete balanced partial double cross (BPDC) mating designd1. For the BPDC(i× j)(k ×l), where i ≠j ≠k ≠ l, in m blocks, we adopt the following model
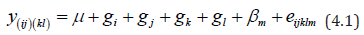
where y(ij)(kl) is the observation on double cross (ij)(kl) from m blocks, m = 1,2,..., p,i, j, k,l = 1,2,..., p;i ≠ j ≠ k ≠ l,μ is the general mean, gi is the effect of ith line, βm is the effect mthblock and eijklm are random errors assumed independent and normally distributed with mean zero and variance σ2.
An incomplete four - way mating design d1 is defined such that every line occurs exactly r times and every four-way cross occurs once or not all [9]. In matrix notation (4.1) can be written as below
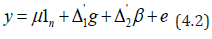
y is an n×1 vector of observations, 1 is an n×1 vector of ones, Ä′1 is an n × p design matrix for lines and Ä′2 is an n × b design matrix for blocks, that is, the (h, l)th element of 1 Ä′1 ( also of Ä′2 ) is 1 if the hth observation pertains to the lth line (also of block) and is zero otherwise. μ is a general mean, g is a p × 1 vector of line parameters, β is a p × 1 vector of block parameters and e is an n × 1 vector of residuals. It is assumed that vector β is fixed and e is normally distributed with mean 0 and Var (e) = σ2IwithCov (β, e) = 0, where I is the identity matrix of conformable order. For the analysis of proposed design d1, the method of least squares leads to the following reduced normal equations for estimating the linear functions of the line effects of lines under model (4.1).
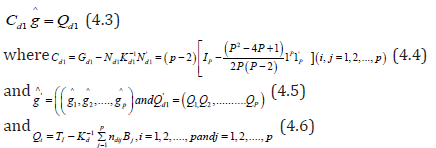
where '
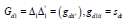
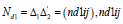
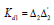
The sum of the elements in each row and each column of Cd1 is equal to zero. Hence rank
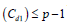
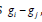
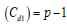
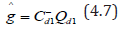
where
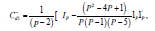
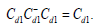
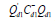
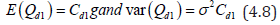
From (4.7), it follows immediately that the using d1 each elementary contrast among line effects is estimated with a variance
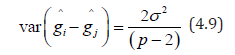
Now let us suppose that the proposed design d1 is replicated u times because if we analysis the proposed design d1 no degrees of freedom is left for the error. Now we consider the following model for replicated BPDC design.
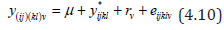
where y(ij)(kl)v is the observation on double cross (ij)(kl) from vth replicate?
v = 1, 2,...,u,i, j, k,l = 1, 2,..., p;i ≠ j ≠ k ≠ l ≠,μ is the general mean,
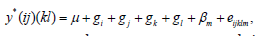
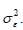
Optimality
design d1 is connected since rank
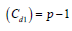
Kiefer (1975) showed that a design is universally optimal in a relevant class of competing design:
a) The information matrix ( the Cd – matrix) of the design is completely symmetric in the sense that Cd has all its diagonal elements equal and all of its off- diagonal elements equal, and
b) The matrix Cd has maximum trace in the class of competing designs, that is, such a design minimizes the average variance of the best linear unbiased estimators of all elementary contrasts among the parameters of interest i.e. the line effects in our context. Now we state the Kiefer criterion of the universal optimality in sense [2] to compare proposed designs optimality with universal optimal designs.
Theorem: For any proposed design d*ε D( p,b,k) be a block design for m-allelcrosses satisfying
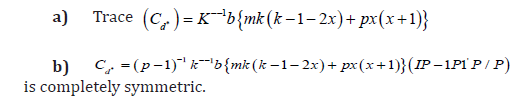
Where X = [2k / p,] where [z] denotes largest integer not exceeding z, Ip is an identity matrix of order p and 1p 1′p is a p × p matrix of all ones. Furthermore, using d* all elementary contrasts among line effects are estimated with variance
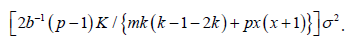
Then d* is universally optimal in D (p, b, k), and in particular minimizes the average variance of the best linear unbiased estimator of all elementary contrasts among the line effects. According to the definition 2.6, the trace of our proposed design
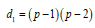
Theorem: The existence of a nested balanced incomplete block design d with parameters
Discussion
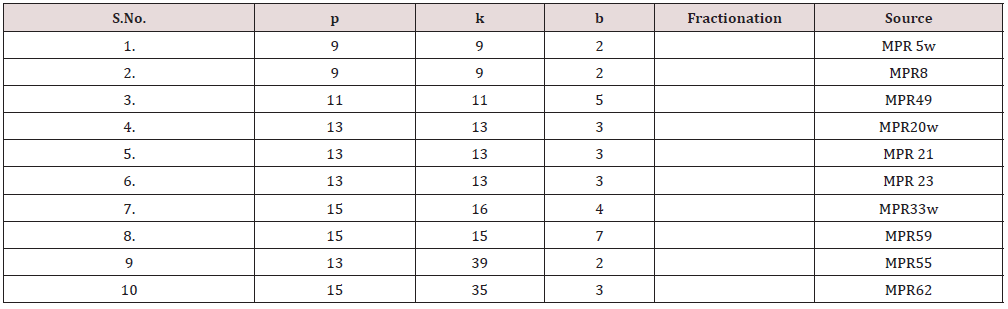
A-Optimal balanced partial double cross designs with p ≤ 16, s ≤ 30 obtained by the above methods from NBIB designs [7], are listed in the following Table 2. These are the designs other than the designs catalogued [12,10,8]. These are the new designs and can be used in agricultural experimentation successfully [13,14].
Table 2: optimal block design for double cross with p ≤ 16, s ≤ 30 generated by using NBIB designs of Morgan [3].
Conclusion
We have presented a method of construction of three series of A-optimal balanced block designs for partial double cross by using nested balanced incomplete block designs. Our proposed Aoptimal block designs for partial double crosses are new.
References
- Bose RC, Shrikahande SS, Bhattacharya KN (1953) On the construction of group divisible incomplete block designs. Ann Math Stat 24: 167-195.
- Singh M, Gupta S, Parsad R (2012) Genetic crosses experiments. In: Design and Analysis of Experiments K Hinkelmann (Eds.), 3: 1-71.
- Morgan JP, Preece DA, Rees DH (2001) Nested balanced incomplete block designs. Discrete Mathematics 231(1-3): 351-389.
- Sharma MK, Tadesse M (2016) Optimal block designs for double cross experiments. Communication in Statistics-Theory and Methods 45(15): 4392-4396.
- Gupta S, Choi K C (1998) Optimal row-column designs for complete diallel crosses. Communication in Statistics-Theory and Methods 27(11): 2827-2835.
- Griffing B (1956) Concepts of general and specific combining ability in relation to diallel crossing system. Aust J Bio Sci 9: 463-493.
- Parsad R, Gupta VK, Gupta S (2005) Optimal Designs for Diallel and Double Cross Experiments. Utilitas Mathematica 68: 11- 32.
- Rawlings JO, Cockerham CC (1962) Analysis of double cross hybrid populations. Biometrics 18: 229-224.
- Hinkelmann KH (1963) Design and Analysis of multi-way genetic cross experiments. Ph.D. thesis submitted to Iowa State University of Science and Technology, USA.
- Das A, Dey A, Dean MA (1998) Optimal designs fordiallel cross experiments. Statistics & Probability Letters 36: 427-436.
- Dey A, Das US, Banerjee AK (1986) Construction of nested balanced incomplete block designs. Calcutta Statist Assoc Bull 35: 161-167.
- Dey A, Midha, Chand K (1996) Optimal designs for diallel crosses. Biometrika 83(2): 484-489.
- Kiefer J (1975) Construction and optimality of generalized Youden designs. Srivastava JN (Eds.), A Survey of Statistical Design and Linear Models. North- Holland Amesterdam pp: 333-353.
- Sharma MK, Tadesse M (2017) Optimal block and row-column designs for CDC methods. Sankhya Ser B 79(2): 278-291.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...