Optimal Efficacy in Light-Activated Biomedical Systems and Nonlinear Laws versus Linear Beer-Lambert Law and Bunsen-Roscoe Reciprocal Law Volume 1 - Issue 5

Jui-Teng Lin*

• New Vision Inc Taipei, Taiwan

Received: March 14,2018;   Published: March 21,2018

Corresponding author: Jui-Teng Lin, New Vision Inc Taipei, Taiwan, Email: jtlin55@gmail.com

DOI: 10.32474/OAJBEB.2018.01.000123

Abstract PDF

---

Abstract

Efficacy of light-activated biomedical processes depends on the tissues (media) optical properties, the photosensitizers, and the light parameters such as its wavelength, energy, intensity, pulse-width, repetition rate and the operation modes. Optimal combination of light fluence (energy density), intensity and irradiation time may be achieved via scaling laws. Beer-Lambert law (BLL) and Bunsen-Roscoe law (BRL, for reciprocity rule) are discussed and compared to new nonlinear scaling laws developed by coupled equation for light intensity and concentration of the photosensitizers. The linear BLL is limited to simple case, when there is no photosensitizer depletion. Type-II photodynamic therapy efficacy follows the BRL (for the case of no external oxygen supply, with P=0), whereas type-I and type-II (with P>0) follow a non-linear non-BRL.

Keywords: Photodynamic Therapy Efficacy; Beer Lambert Law; Bunsen Roscoe Law

Abbrevations: BLL: Beer Lambert Law; BRL: Bunsen Roscoe Law; BGK: Bhatnagar Gross Krook

Introduction

One of the major applications of biomedical engineering is to use light (lasers or LED) to activate biomedical systems for clinical therapy. There are two important laws related to the fundamental and efficacy of the photo-biological systems: the Beer-Lambert law (BLL) and the Bunsen-Roscoe law (BRL) of reciprocity [1-3]. BLL also known as the Beer-Lambert-Bouguer law which relates the attenuation of light in absorbing media [1]. The law is commonly applied to chemical analysis measurements and physical optics. In mathematical physics, this law is a solution of the Bhatnagar-Gross- Krook (BGK) equation. The BLL is the linear relationship between absorbance and concentration of an absorbing media at various traveling depth.

The linearity of BLL is limited by chemical and instrumental factors and the causes of nonlinearity include: deviations in absorption coefficients at high concentrations due to electrostatic interactions between molecules; scattering of light due to particulates in the sample; fluorescence or phosphorescence of the sample; changes in refractive index at high analyte concentration; shifts in chemical equilibria; depletion (breaching) photosensitizer concentration; and non-monochromatic radiation. These nonlinear features result optimal conditions for maximum efficacy of light- activated biological outcomes. The optimal conditions could be achieved by, for examples, optimal analytic concentration, light and/or drug dose, light intensity and light penetration depth or analytic concentration profiles.

Another photo-biological law, the Bunsen-Roscoe law (BRL) of reciprocity stating that the effect of a photo-biological reaction is proportional only to the total irradiation fluence (E=It), or the product of intensity (I) and exposure time (t). To achieve the same efficacy, the required exposure time based on BRL is given by t=E/I. Based on BRL, treatment time may be shortened by using a higher intensity while maintaining the similar efficacy [4]. The linear BRL has limitation as that of BLL. These study intents to analyze and compare the BLL, BRL and the newly derived nonlinear law (NLL). A generalized, time dependent Beer-Lambert law (BLL) and the non-BRL optimal conditions will be introduced. Fluence (energy) and intensity scaling laws in various photo-biological systems will be given as clinical examples for the developed mathematical formulas (scaling laws).

Method

Laser-Matter Interaction

Light (laser or LED) and tissue (or other media) interaction, in general, could be categorized into three processes: (a) pure thermal, (b) non-thermal, and (c) combined thermal and nonthermal effects. Light can be reflected, absorbed, scattered or transparent to the matter. These processes are governed by not only the tissues (media) optical properties, the photosensitizes, but also the laser/light parameters such as its wavelength, energy, intensity, pulse-width, repetition rate and the operation modes, continuous wave (CW) or pulsed mode. We will show example of non-thermal photodynamic therapy (PDT) to demonstrate the limitation of BLL and BRL. A generalized BLL is derived to include the depletion of photosensitize concentration causing the increasing of the dynamic intensity:

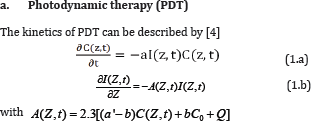
where C(z,t) is the concentration of the photosensitize (PS); a= 83.6a’wp, with w is the light wavelength; p being the quantum yield for the PDT process; Q is the tissue absorption coefficient; a’ and b are the extinction coefficient of the photosensitize and its photolysis products.

We note that due to the depletion of C(z,t) in time, the light intensity, I(z,t), in general is time-dependent and maybe given by a generalized, time dependent Beer-Lambert law (BLL) as: I(z,t)=I₀ exp[-A(t)z], where A(t) has an initial value (at t=0) A1=2.3(a’C₀+Q), and decreases to a steady-state, A2=2.3(bC₀+Q), where b0[b+(a’-b)exp(-b’t)], and b’=aI₀exp(-A’z); with A’ is the mean value A’=0.5(A1+A2). For small b’t, B is approximated by B=2.3C₀[a’- (a’-b)b’t], and A(t)=A0-b₁t, with A₀=A1+2.3C₀a’, b1=2.3C₀(a’-b)b’. Our previous model [5] assumed a time-independent A(t), or b₁=0. The linear BLL is limited to when C(z,t) is time independent, and not depleted by the light. All the nonlinear features of BLL and BRL are resulted from the depletion of C(z,t), which also causes the dynamic feature of light intensity, defined by A(t), which is a decreasing function of time. The efficacy of a photo-biological system is proportional to a S-function [4] defined by the timeintegration of [IC]ⁿ

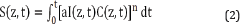
Where n is a scaling factor defined by the "nature" of the PDT processes, having a range of 0.3 to 1.2. Using the approximated analytic solution of Eq. (1) C(z,t)=C₀exp[-aI’(z)t], with I’(z)=I₀exp(- A’z), and I(z,t)=I₀exp[-(A0-b₁t )z], we obtain

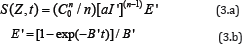
with B’=n(aI’-b₁), with b₁=2.3C₀(a’-b)aI₀exp(-A’z). Our previous model [5] assumed a time-independent A(t), or b₁=0. Eq. (3) is a more general case including the dynamic of light intensity, or the time dependent A(t).

Results and Discussions

Influence of C(z,t) depletion

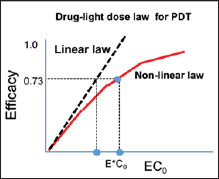
Without the depletion of C(z,t)=C₀, S is a linear function of the light fluence E=tI. The nonlinear feature is resulted from the depletion of C(z,t), which has a typical profile shown in Figure 1. The nonlinear feature of S is shown in Figure 2. Also shown are the threshold products (E*C₀) which is underestimated in linear drug- light dose law [6].

Figure 1: The normalized PS concentration profile at exposure time t= (0, 12, 25, 50, 115) seconds (for curves 1, 2, 3, 4, 5) [4].

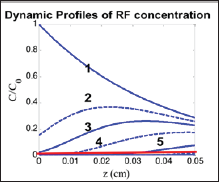
Figure 2: The efficacy versus product [ECO] showing the Bunsen-Roscoe law (BRL, dashed curve) and nonlinear law (solid curve). Also shown are the threshold products (E*C₀).

The scaling laws

With the depletion of C(z,t), the nonlinear laws are discussed as follows. For transient state (with B’<<1), Eq. (4) gives a scaling law of Sα[C₀αI]ⁿt, or Sα[C₀αE]"t^(1-n), with E = E₀ exp(-A't), E₀ = tI₀ is the light fluence (dose). While at steady-state, with exp(-B'i) = 0 , we obtain a totally different scaling, Sα( C)[ αl ]^(n-1)/(i - b₂) or Sα(C₀”)[αE\"i^<1_”⁾/(i-b), with b₂ = 2.3C₀(α'-b), which is independent to the dose, in the first order approximation.

Scaling laws for various photo-medical systems maybe analyzed as follows.

A. Simple case (follows BRL)

For n=1, Eq. (4) becomes S = C₀[1 - exp(-αE)], which is only governed by the light fluence (E), i.e., it follows the Bunsen-Roscoe law (BRL) that same fluence will achieve same efficacy (independent to its intensity). Examples of this BRL-case include type-II corneal crosslinking and the treatment of age related macular degeneration (AMD) [6], anti-cancer [7], where the photo-produced singlet oxygen, which defines the efficacy, is proportional to [IC][O₂], with n=1. Therefore, the dose (E=tI) solely determines the efficacy which follows the BRL. In this case, there is no optimal value of dose, intensity or photosensitizer concentration. S is just a nonlinear increasing function of dose and reaches its steady-state. As shown by Figure 3, without external oxygen supply (P=0), different intensities with the same dose will achieve the same steady-state efficacy, although their rising slopes are different [4]. However, for P>0, as shown by Figure 4, the overlap feature fails resulted form the extra time-dependent term Pt in the oxygen concentration, [O₂]. The BRL also apply to the PDT in retina treatment, where the photosensitizer dose (or concentration), the light fluence (E) and the irradiation time (t) follow our reciprocal drug-light dose law given by the product EC₀. Various combinations of: full-dose, halfdose, full-fluence and half-fluence have been reported [6].

Figure 3: The S function for type-II PDT, showing S versus time (t) for light intensity of I₀= (50,100, 200) mW/cm², (for curve from left to right); and S versus fluence (right figure), where all the curves overlap to one for the case of P=0 (no external oxygen supply).

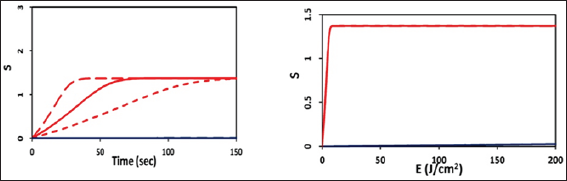
Figure 4: Same as Figure 3, but with external oxygen supply, P=0.07 (uM/s).

B. Non-BRL case (with n=0.5)

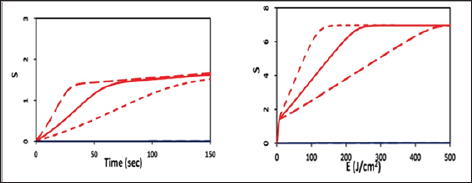
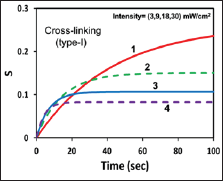
For n=0.5, representing a Type-I, PDT or corneal crosslinking (CXL), the S-formula shows the Type-I efficacy at transient state (for small fluence) is proportional to tI₀°'⁵ . However, at steady-state, it is a nonlinear increasing function of [C₀/1₀]05 or [c₀o/e₀ ]⁰⁵ .These scaling laws show that higher intensity has lower steady-state efficacy than lower intensity, as shown by Figure 5 for intensity of (3,9,18,30) mW/cm² [4]. To achieve the same CXL efficacy, higher PS concentration requires higher UV light intensity; and for the same dose, higher UV light intensity requires a longer exposure time. We note that type-II, PDT efficacy follows the BRL (for the case of no external oxygen supply, with P=0), whereas type-I and type-II (with P>0) follow a non-linear non-BRL.

C. General case

The efficacy of so-called low level laser therapy (LLLT) stimulated photo-biological and photochemical reactions may be described by a scaling law with 0.3<n<1.2, depending on the tissues (media) optical properties, the photosensitizers and the kinetics involved. Clinical data are required to fit the scaling laws. Therefore, variation of exposure time and irradiance may account for conflicting results in the literature. Duzgoren et al. [8] recently report the optimal combination of light intensity and dose for maximum efficacy. However, their do not present enough data to show the actual value of n in the scaling law. Our theory predicts the n value should be approximately 0.5 to 0.8 for most LLLT procedures.

Figure 5: Efficacy of type-I PDT showing the non-BRL law; curves (1,2,3,4) for intensity of (3,9,18,30) mW/cm² [4].

D. Optimal efficacy

Figure 6: Optimal dose E* related to the Arndt-Schulz-Law [9] showing an optimal therapeutic window, (E1 and E2), which can provide a safe and effective therapy.bv

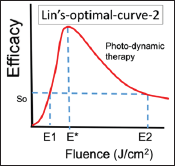
Taking Eq. (4) dS / dE = 0, we may find the optimal dose given by exp(-naE*)=(1-n)/[(1-n)+naE*]. For the case of n=0.5, we obtain E* = I₀exp(-AZ*) = 1,25 /(0.5a) , which also defines the optimal depth Z* = (1/A)ln[aE'/2.5], with z* in cm, and E* in J/ cm². Figure 6 shows an example for optimal feature which is also related to the Arndt-Schulz-Law (ASL) [9] that there is an optimal therapeutic window, which can provide a safe and effective therapy. Greater details based on the numerical simulations of Eq. (1) will be presented elsewhere.

Conclusion

Efficacy of photo-biological processes depends not only on the tissues (media) optical properties, the photosensitizes, but also the laser parameters. Optimal combination of light energy (dose), intensity and irradiation time may be achieved via the nonlinear scaling laws. The linear BLL is limited to simple cases, when there is no photosensitize depletion. Type-II PDT efficacy follows the BRL (for the case of no external oxygen supply, with P=0), whereas type-I and type-II (with P>0) follow a non-linear non-BRL.

References

1. Lambert JH (1760) Photometria sive de mensura et gradibus luminis, colorum et umbrae. Eberhardt Klett, Germany.
2. Bunsen RW, Roscoe HE (1862) Photochemical researches-Part V: On the measurement of the chemical action of direct and diffuse sunlight. Proc R Soc Lond 12(1862-1863): 306-312.
3. Khurana M, Moriyama EH, Mariampillai A (2008) Intravital highresolution optical imaging of individual vessel response to photodynamic treatment. J Biomed Opt 13(4): 040502.
4. Lin JT (2018) Efficacy S-formula and kinetics of oxygen-mediated (type-II) and non-oxygen-mediated (type-I) corneal cross-linking. Ophthalmology Research. 8(1): 1-11.
5. Lin JT (2018) Lin-scaling-law for optimal efficacy in photo-biological systems versus Arndt-Schulz-Law and Bunsen-Roscoe law. Med Devices Diagn Eng 3: 120-123.
6. Dhiran NA, Yang Y, Somani S (2017) Long-term outcomes in halfdose verteporfin photodynamic therapy for chronic central serous retinopathy. Clinical Ophthalmology 11: 2145-2149.
7. Lin JT (2018) Analysis of kinetics and efficacy of anti-cancer via oxygen- enhanced photodynamic therapy. J Cancer Research Updates 7: 21-26.
8. Duzgoren I, Ruhi MK, Gulsoy M (2017) Effect of different laser power densities on photobiomodulation of L929 cell line. Proc of SPIE OSA, Europe.
9. Sommer AP, Pinheiro AL, Mester AR (2001) Biostimulatory windows in low-intensity laser activation: Lasers, scanners, and NASAs light- emitting diode array system. J Clinical Laser Medicine Surgery 19: 29-33.