Elimination of Pseudo Initial Stress for Proposed Invariants based Hyper elastic Strain Energy Volume 1 - Issue 4

NZ Bayat and K Narooei*

• Department of Materials Science Engineering, KN Toosi University of Technology, Iran

Received: February 27, 2018;   Published: March 07, 2018

Corresponding author: K Narooei, Assistant Professor, Department of Materials Science Engineering, K N Toosi University of Technology, Iran, Tel: 98-21-84063283; Email: knarooei@kntu.ac.ir

DOI: 10.32474/OAJBEB.2018.01.000117

Abstract PDF

---

Abstract

Although fitting of experimental data is important in selection of the best hyper elastic strain energy function, the zero stress condition in the initial (unstressed) configuration also should be taken into account. Therefore, in the current research a modification for an invariants based model was developed to eliminate the pseudo initial stress. To this goal, additional terms were added to hyper elastic strain energy as a function of the right Cauchy-Green deformation tensor. To justify the proposed algorithm, uniaxial loading of liver tissue and unfilled silicone rubber were studied via constitutive modeling in VUMAT user subroutine of ABAQUS software. Excellent agreement between the experimental and numerically predicted stress-stretch curves showed that the modified strain energy function enables to characterize the mechanical behavior of the liver tissue and unfilled silicone rubber. As the deformed shapes of soft tissues are important especially in the surgery operations, the effect of modification on the final deformed geometry was investigated. Results were shown the deformed profile of the modified and unmodified hyper elastic strain energy models were different.

Keywords: Modified invariants model; Isotropic material; Constitutive modeling; Hyper elastic materials; Unstressed configuration.

Introduction

In the last few years, many studies have concentrated on the accurate prediction of nonlinear behavior of materials such as soft tissues and rubber like materials. Modeling of the hyper elastic behavior involves selection of an appropriate strain energy function, determination of material constants, and constitutive modeling to investigate the response of model in real loading conditions [1,2]. In this context, a large number of hyper elastic strain energy functions have been proposed by researchers [3]. In general, the hyper elastic strain energy functions have been based on invariants or principal values of the stretch (or Cauchy-Green) tensor [4]. Due to the nonlinear mechanical behavior of soft tissues and rubber like materials, constitutive equations that calibrated with one loading condition can not necessarily evaluate the mechanical response under other loading modes [5-8].Therefore, in order to predict accurately the mechanical properties of biological tissues, experimental tests in various loading conditions are preferred [9-11].

Meunier et al. [12] performed experimental and numerical tests to describe the mechanical behavior of unfilled silicone rubber. Results indicated that the Haines-Wilson, Gent, and Ogden models can present proper behavior of the silicone rubber and the Mooney-Rivlin model prediction is not satisfactory. Jamshidi and Ahmadianused the Mooney- Rivlin, polynomial, Yeoh, and Ogden models to represent the mechanical properties of heart tissues and found the Yeoh material model as the best one [13]. Kaster et al. [14] employed the polynomial, Yeoh, Arruda- Boyce and Ogden models for accurate characterization of the mechanical behavior of brain tissue. Although they pointed out the Yeoh model is more efficient because of its accuracy, fewer material parameters, and shorter computational time, but this model depends only on the first invariant of stretch tensor and in pure shear could not predict appropriate behavior [4]. Gokgol et al. [15] used the five terms Mooney-Rivlin model to validate the experimental results on the bovine liver tissue for estimation of fracture toughness. They used the inverse solution to estimate the material parameters.

In addition to conventional hyper elastic strain energy functions, many researchers used a combination of mathematical functions such as polynomial, exponential, power or logarithmic forms. Research of Fung et al. [16] was one of the first studies on the combined mathematical functions for better characterization of the nonlinear behavior of materials. Gao et al. [17] proposed a new constitutive model by adding the logarithmic function to Ogden hyper elastic model. The proposed model represented the liver tissue behavior under tension, compression, and pure shear deformation modes in large strains. In order to describe the significance of accurate zero-strain (or stress) in estimation of nonlinear material properties, Chui et al. [18] used the full cycle of compression and tension on the liver tissue. They proposed a new constitutive equation based on the combination of polynomial and logarithmic functions. In order to simulate the indentation test of porcine liver tissue, Fu and Chui [19] used the compression and tension experimental data for estimation of material parameters and showed the logarithmic-polynomial model is partly better than the five terms Mooney- Rivlin model. Darijani and Naghdabadi [20] proposed hyper elastic strain energy models based on polynomial, power, logarithmic and exponential function of principal stretches to capture the large deformation behavior. Khajehsaeid et al. [11] proposed a strain energy function for large deformation of isotropic incompressible rubber-like materials with combination of exponential and logarithmic functions and found the proposed model presents good agreement with experimental data. Hosseinzadeh et al. [21] applied the Mooney- Rivlin and Ogden models as well as the general exponential- exponential and general exponential-power law models for investigation of the demineralized and deproteinized bovine cortical femur bones.

Their results illustrated that among the employed models the general exponential- exponential and general exponential-power law models have a good agreement with the experimental results and material stability. Elyasi et al. [22] used the general exponential and invariants models to find the best hyper elastic function that fit the experimental data of extensor apparatus. They investigated the material instability and accordingly obtained the stress distribution in flexion movement. Mansouri and Darijani [4] proposed a new framework for strain energy functions of the isotropic hyper elastic materials in terms of the first and second invariants of the right Cauchy-Green deformation tensor. According to their results, the in variants model illustrates precisely the stress- strain behavior of elastomers and soft tissues in special test conditions and its performance for general cases should be investigated in FE-based modeling techniques.

In the current research, the invariants model proposed by Mansouri and Darijani is modified to consider the initial free stress configuration and elimination of spurious mathematical stress. To justify the significance of initial free stress configuration, the deformation behavior of the porcine liver tissue and silicon rubber is simulated. To this end, in the next sections firstly the modification of the hyper elastic model and accordingly the constitutive modeling are presented. Finally, the results of simulations will be presented and discussed.

Hyper Elastic Model and Unstressed Configuration Modification

As it was mentioned, Darijani and Naghdabadi [20] proposed hyper elastic strain energy models based on a combination of polynomial, power law, logarithmic and exponential functions. Hyper elastic strain energy functions not only should be able to fit the experimental data, but also should be as simple as possible and having a small number of parameters. Meanwhile, Mansouri and Darijani [4] generalized the models of Darijani and Naghdabadi [20] and they called the hyper elastic functions as general power and general exponential models. Their hyper elastic functions were based on the first and second invariants of the right Cauchy-Green deformation tensor and they showed the robustness of models in describing the mechanical behavior of isotropic materials. Thereby, in this study the model in terms of the first ( I₁) and second ( i₂ ) invariants of the right Cauchy-Green deformation tensor ( C) was used. In the following, for simplicity, this model is called the invariants model and it can be expressed as [4]:

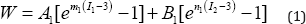
Where A₁, B₁ , m₁, and n₁ are the unknown material parameters and W represents the hyper elastic strain energy function. The second Piola-Kirchhoff stress components ( S) can be derived from the hyper elastic strain energy function as [21,22]:

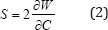
Derivatives of the invariants of the symmetric tensor C with respect to itself can be mentioned as:

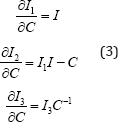
Where I is identity tensor. Assuming of Eqs. 1, 2 and 3, the second Piola-Kirchhoff stress can be derived as:

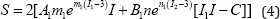
Substituting of the initial (undeformed) configuration condition ( I₁ = 3,I₂ = 3,C = I) in Eq. 4 the following initial values can be obtained:

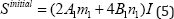
Where 5 ^initial represents the initial stress values and as it can be seen it only includes the normal components. It should be noted the initial stress does not any physical interpretation like the physical initial stresses in biomaterials or residual stresses in some elastomers. Therefore, it has the mathematical sources (spurious or pseudo stresses) and it should be eliminated. Indeed, the constant "-1" in Eq. 1 was added to consider the zero value for the hyper elastic strain energy function in the initial configuration as a basic requirement [4-20]. However, applying of Eq. 2 results to mathematical initial pseudo stress presented in Eq. 5. In order to consider the zero initial stress condition, the constraint term was added to Eq. 1 and the modified strain energy equation was derived as:

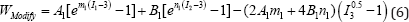
Where, W_Modify is the modified strain energy function that consists of the invariants model terms and the zero initial stress constraint. Moreover, the initial energy yet is zero and as Ogden et al has mentioned it is one of the methods to impose a constraint on the hyper elastic strain energy [23-26]. Regarding Eqs. 2, 3 and 6the modified second Piola-Kirchhoff stress can be stated as:

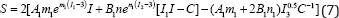
Now, by inspecting of Eqs. 6 and 7 it could be ensured the stress and energy are zero in the initial configuration.

Constitutive Modeling

To use a hyper elasticstrainenergy functionfor anincompressible material, another constraint due to incompressibility should be imposed on the hyper elastic energy function. In order to apply the incompressibility, Eq. 6 should be modified as [27]:

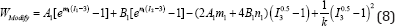
Here, k represents a small number and the incompressibility condition is imposed by the penalty method. Considering of Eqs.2 and 8, the second Piola-Kirchhoff stress components in the presence of the incompressibility condition could be stated as:

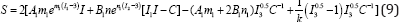
Now by inspecting of Eqs. 8 and 9 the initial stress and energy are zero and the incompressibility condition is also imposed. In order to implement the above formulas in VUMAT user subroutine of the ABAQUS software, the second Piola-Kirchhoff stress should be converted to the co rotational Cauchy stress (σ^ )by the following relation:

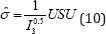
Here U represents the right stretch tensor and S the second Piola-Kirchhoff stress tensor.

Experimental Data

In order to evaluate the modified model, two datasets including tension of porcine liver tissue and compression of unfilled silicone rubber have been used from literatures. The nonlinear biomechanical property of the liver tissue was extracted from experimental study of Gao et al. [17]. Mansouri and Darijani [4] utilized this test data for proofing of robustness of the invariants model and showed the invariants model fitted both of the pure shear and uniaxial tension loading. The silicone rubber is common material in biomechanical applications because of its unique properties and excellent biocompatibility [12-27].The material constants of the porcine liver tissue and unfilled silicone rubber can be seen in Table 1.

Table 1: Material constants of the porcine liver tissue and unfilled silicone rubber [4].

Simulations

Among several types of virtual surgery simulators, the finite element method (FEM) has been commonly used. This method is useful for solving of problems with complex geometry and loading as well as complex nonlinear materials response. This method can be an appropriate method for analysis of the materials stress and strain [28-30] because of realistic materials behavior.

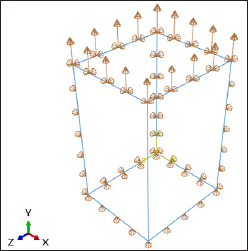
A 3D deformable model was built to simulate the uniaxial tension of porcine liver sample. The length, width, and thickness of the sample were considered as 25, 15, and 17mm respectively similar to the experimental conditions. The 8-node linear brick elements with reduced integration and hourglass control (C3D8R element) were used for simulation. Reduced integrations and enhanced hourglass control were utilized to prevent the volumetric locking and elimination of numerical instability [31] .This model consists of 7488 nodes and 6375 elements. The boundary conditions were assigned according to experimental (Figure 1) and geometry symmetry conditions such that the bottom of the sample was fixed in the Y direction, the upper surface was stretched in the Y direction by and the X and Z directions were fixed. The material parameters of Table 1 were assigned to the invariants model as the material properties.

Figure 1: Geometry and boundary conditions in uniaxial tension test of porcine liver.

The silicon rubber three dimensional (3D) model was created for the compression test simulation. Using symmetry constraints, only quarter of the specimen was considered to increase the numerical stability and reduce the computational time. The height of 20 mm and diameter of 37 mm similar to experimental sample was considered. The compression platen was modelled as a rigid body with diameter of 60 mm. The contact between the platen surface and the rubber specimen were applied. Because in experimental the silicone grease was used as lubricant, the Coulomb friction coefficient between the platen and rubber was considered as 0.005. The simulation was performed by applying a displacement of to the platen in the vertical direction to produce the maximum stretch of 0.48.The applied boundary conditions to the sample were shown in Figure 2. The reaction force and displacement were calculated along the loading direction in the reference point of platen. By dividing of the reaction force to the initial surface of sample, the nominal stress was calculated. The simulations details of two tests were summarized in Table 2 and (Figures 2 ).

Table 2: Characteristics of 3D finite element models.

Figure 2: Geometry and boundary conditions in uniaxial compression test of silicon rubber.

Results and Discussion

In order to examine the proposed modification on the hyper elastic model, in this section the results of porcine liver tension and silicon rubber compression are presented and discussed.

Porcine Liver Tension

For simulation of the porcine liver tissue behavior in uniaxial tension, the invariants model was used. As mentioned by previous researchers [5-10] a hyper elastic model that enables to simultaneously fit all loading conditions and represents material stability could be considered as a suitable model for simulation of finite deformation in complex geometry and loadings. In other hand, a satisfactory prediction significantly depends on the accuracy of geometrical model and constitutive equation [32].The results of simulations with both of the modified and unmodified invariants model were illustrated in Figure 3. As it can be seen from (Figure 3), there are significant differences between the results of the unmodified model and the experimental data. According to definition of isotropic stress free initial configuration, the reference state for an isotropic model should be undistorted and stress-free (zero-strain state) [33]. As it can be seen in Figure 3, by applying the unstressed initial configuration condition on the modified model, the results are very close to the experimental curve.

Figure 3: Effect of modification on stress-stretch curve of tension test of porcine liver (experimental data from Gao et al. [17]).

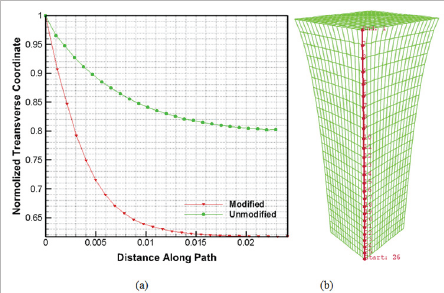
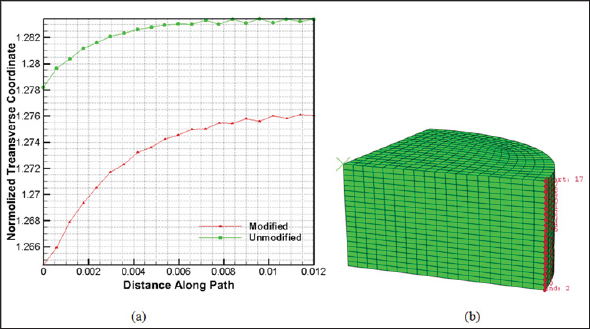
The von Mises stress contours of the porcine liver tension simulation for the modified and unmodified models are provided in Figure 4. To be clear the difference of the deformed geometries resulted from the modified and unmodified models, in Figure 5 the normalized coordinate with respect to the initial coordinate of nodes (i.e. J , where X is the initial coordinate and X is the current coordinate) were plotted against to the distance along the free edge (from start to end node). As it can be recognized the error due to use of unmodified formulation can be significant and it is known the deformed profile in the biomechanics application has great importance in the interpretation of loading results. In addition, the mesh convergence study was revealed increasing of elements do not impact the results.

Figure 4: Tension test simulations of :(a)Modified and (b) unmodified invariants model.

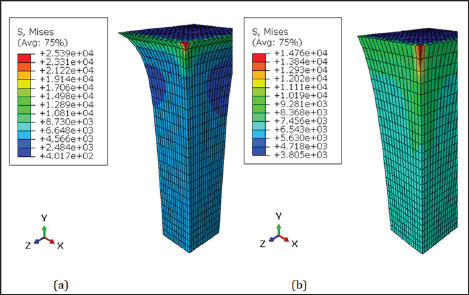
Figure 5: (a) Normalized x coordinate of the free edge versus distance along this edge and (b)Path of free edge for tension test.

Silicon Rubber Compression

For further investigation of the modification of hyper elastic model, the compression of the unfiled silicon rubber was studied. This problem is operational in the simulation of materials behavior especially the soft tissues as in plenty of the surgery operations, the soft tissue is in contact with the surgery devise. Therefore, understanding the soft tissue behavior in this kind of tests can be helpful in the surgical simulations [14-19,31-34]. The stress-stretch curves obtained from the modified and unmodified invariants model for compression of unfiled silicon rubber were shown in Figure 6. As it can be seen when the unmodified formulation was used, it was not possible to capture the nonlinear behavior of the silicon rubber. On the other hand, the modified model showed a good agreement with the experimental data.

Figure 7 illustrates the von Mises stress contours and Different stress distribution can be seen for the modified and unmodified formulations. The normalized z coordinate with respect to the initial coordinate (Z , where Z is the initial coordinate and z is the current one) were plotted against to the distance along the free edge in Figure 8. As in the porcine liver tension, there is discrepancy between two formulations.

Figure 6: Effect of modification on the stress-stretch curve of compression test of unfiled silicon rubber (experimental data from Meunier et al. [12]).

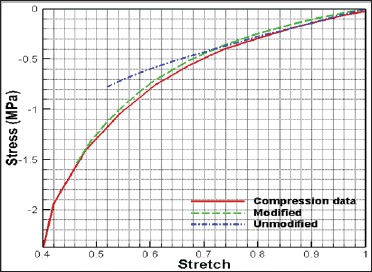
Figure 7: Effect of modification on the stress-stretch curve of compression test of unfiled silicon rubber (experimental data from Meunier et al. [12]).

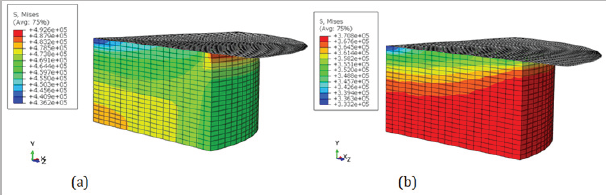
Figure 8: Effect of modification on the stress-stretch curve of compression test of unfiled silicon rubber (experimental data from Meunier et al. [12]).

Conclusion

It was observed by previous researches the invariants model is enable to fit the experimental data of tension, compression, and balanced biaxial tests. As this model does not provide the zero initial stress, in this study, the role of unstressed configuration on the finite element results was investigated. To this goal, the initial stress was removed from the hyper elastic strain energy via a function of the third invariant of the right Cauchy-Green deformation tensor. Inspection of the new hyper elastic strain energy revealed the zero energy and zero stress could be captured in the unstressed initial configuration. To justify the effects of the modification, the deformation behavior of porcine liver tissue and unfilled silicone rubber were considered. Results indicated that there is a significant difference between the predicted and experimental stress-stretch curves when the modification is not considered. In addition, it was seen the deformed geometry were different for the modified and unmodified models.

Acknowledgement

The authors would like to thank the K. N. Toosi University of Technology, Tehran, Iran, for the financial support and research facilities used in this work.

References

1. R Moran JH, Smith JJ, García (2014) Fitted hyperelastic parameters for Human brain tissue from reported tension, compression, and shear tests. Journal of biomechanics 47(15): 3762-3766.
2. S Umale, C Deck, N Bourdet, P Dhumane, L Soler, et al. (2013) Experimental mechanical characterization of abdominal organs: liver, kidney & spleen. Journal of the mechanical behavior of biomedical materials 17: 22-33.
3. T Beda (2014) An approach for hyperelastic model-building and parameters estimation a review of constitutive models. European Polymer Journal 50: 97-108.
4. MR Mansouri, H Darijani (2014) Constitutive modeling of isotropic hyperelastic materials in an exponential framework using a self-contained approach. International Journal of Solids and Structures 51(25-26): 4316-4326.
5. MA Hassan, M Hamdi, A Noma (2012) The nonlinear elastic and viscoelastic passive properties of left ventricular papillary muscle of a Guinea pig heart. Journal of the mechanical behavior of biomedical materials 5(1): 99-109.
6. A. Kossa, S Berezvai (2016) Novel strategy for the hyperelastic parameter fitting procedure of polymer foam materials. Polymer Testing 53: 149-155.
7. G Sommer, M Eder, L Kovacs, H Pathak, L Bonitz, et al. (2013) Multiaxial mechanical properties and constitutive modeling of human adipose tissue: a basis for preoperative simulations in plastic and reconstructive surgery. Acta biomaterialia 9(11): 9036-9048.
8. C D Untaroiu, Y C Lu, S K Siripurapu, A R Kemper (2015) Modeling the biomechanical and injury response of human liver parenchyma under tensile loading. Journal of the mechanical behavior of biomedical materials 41: 280-291.
9. X Jin, F Zhu, H Mao, M Shen, K H Yang (2013) A comprehensive experimental study on material properties of human brain tissue. Journal of biomechanics 46(16): 2795-2801.
10. J H Smith, J J García, Constitutive modeling of brain tissue using Ogden-type strain energy functions. Fifth Biot Conference on Poromechan- ics pp. 2140-2147.
11. H Khajehsaeid, J Arghavani, R Naghdabadi (2013) A hyperelastic constitutive model for rubber-like materials. European Journal of Mechan- ics-A/Solids 38: 144-151.
12. L Meunier, G Chagnon, D Favier, L Orgeas, P Vacher,(2008) Mechanical experimental characterisation and numerical modelling of an unfilled silicone rubber. Polymer Testing 27(6): 765-777.
13. M Jamshidi, M Ahmadian (2013) Investigation of the effect of high+ Gz accelerations on human cardiac function. Journal of the mechanical behavior of biomedical materials 27: 54-63.
14. T Kaster, I Sack, A Samani,(2011) Measurement of the hyperelastic properties of ex vivo brain tissue slices. Journal of Biomechanics 44(6): 11581163.
15. C Gokgol, C Basdogan, D Canadinc (2012) Estimation of fracture toughness of liver tissue: Experiments and validation. Medical engineering & physics 34(7): 882-891.
16. Y Fung, S Cowin (1994) Biomechanics: mechanical properties of living tissues. Journal of Applied Mechanics 61: 1007.
17. Z Gao, K Lister, J P Desai (2010) Constitutive modeling of liver tissue: experiment and theory. Annals of biomedical engineering 38(2): 505-516. 18.
18. C Chui, E Kobayashi, X Chen, T Hisada, I Sakuma (2004) Combined compression and elongation experiments and non-linear modelling of liver tissue for surgical simulation. Medical and Biological Engineering and Computing 42(6): 787-798.
19. Y Fu, C Chui (2014) Modelling and simulation of porcine liver tissue indentation using finite element method and uniaxial stress- strain data. Journal of biomechanics 47(10): 2430-2435.
20. H Darijani, R Naghdabadi (2010) Hyperelastic materials behavior modeling using consistent strain energy density functions. Acta mechanica 213(3-4): 235-254.
21. M Hosseinzadeh, M Ghoreishi, K Narooei (2016) Investigation of hyperelastic models for nonlinear elastic behavior of demineralized and deproteinized bovine cortical femur bone. Journal of the mechanical behavior of biomedical materials 59: 393-403.
22. N Elyasi, K Karimi Taheri, K Narooei, A Karimi Taheri (2017) A study of hyperelastic models for predicting the mechanical behavior of extensor apparatus. Biomechanics and Modeling in Mechanobiology 16(3): 1077-1093.
23. R W Ogden (1997) Non-linear elastic deformations: Courier Corporation.
24. J Humphrey, F Yin (1987) A new constitutive formulation for characterizing the mechanical behavior of soft tissues. Biophysical journal 52(4): 563-570.
25. L Cheng, B Hannaford (2015) Finite Element Analysis for evaluating liver tissue damage due to mechanical compression. Journal of biomechanics 48(6): pp. 948-955.
26. M Gilchrist, J G Murphy, B Rashid (2012) Generalisations of the strain-en- ergy function of linear elasticity to model biological soft tissue. International Journal of Non-Linear Mechanics 47(2): 268-272.
27. T Rey, G Chagnon, J B Le Cam, D Favier (2013) Influence of the temperature on the mechanical behaviour of filled and unfilled silicone rubbers. Polymer Testing 32(3): 492-501.
28. A Mendizabal, I Aguinaga, E Sánchez (2015) Characterisation and modelling of brain tissue for surgical simulation. Journal of the mechanical behavior of biomedical materials 45: 1-10.
29. F Dogan, M S Celebi (2016) Quasi-non-linear deformation modeling of a human liver based on artificial and experimental data. The International Journal of Medical Robotics and Computer Assisted Surgery 12(3): 410420.
30. M Kauer, V Vuskovic, J Dual, G Székely, M Bajka (2002) Inverse finite element characterization of soft tissues. Medical Image Analysis 6(3): 275-287.
31. K Lister Z, Gao, J P Desai (2011) Development of in vivo constitutive models for liver: application to surgical simulation. Annals of biomedical engineering 39(3): 1060-1073.
32. C D Untaroiu, Y C Lu (2013) Material characterization of liver parenchyma using specimen-specific finite element models. Journal of the mechanical behavior of biomedical materials 26: 11-22.
33. Z Gao, J P Desai (2010) Estimating zero-strain states of very soft tissue under gravity loading using digital image correlation. Medical image analysis 14(2): 126-137.
34. M G Zhang, Y P Cao, G Y Li, X Q Feng (2014) Pipette aspiration of hyperelastic compliant materials: Theoretical analysis, simulations and experiments. Journal of the Mechanics and Physics of Solids 68: 179-196.
35. Scott T Lovald, Andrew Rau, Steven Nissman, Nicoli Ames, John McNulty, et al. (2017) Finite element analysis and experimental evaluation of penetrating injury through the cornea. Journal of the Mechanical Behavior of Biomedical Materials 66(1): 104-110.
36. S Kling, N Bekesi, C Dorronsoro, D Pascual, S Marcos (2014) Corneal viscoelastic properties from finite-element analysis of in vivo air-puff deformation. PLoS One 9(8): e104904.