A Novel Finite Element Model on Atherosclerotic Plaques: Effect of Heart Rate Volume 2 - Issue 2

Mehrdad Zareh, Bahman Naser and Hadi Mohammadi*

• The Heart Valve Performance Laboratory, School of Engineering, Faculty of Applied Science, University of British Columbia, Canada

Received: April 06,2018;   Published: April 16,2018

Corresponding author: Dr. Hadi Mohammadi, PEng, School of Engineering, Faculty of Applied Science, University of British Columbia, Okanagan, Kelowna, BC, Canada, V1V 1V7, Tel: (250) 807-9920; Email: hadi.mohammadi@ubc.ca

DOI: 10.32474/OAJBEB.2018.02.000135

Abstract PDF

---

Abstract

Atherosclerotic plaques are highly heterogeneous, nonlinear materials with uncharacteristic structural behaviors. It is well known that mechanics of atherosclerotic plaques significantly depend on plaque geometry, location, composition, and loading conditions. Computational studies have shown great potential to characterize this mechanical behavior. Different types of plaque morphologies and mechanical properties have been used in a computational platform to estimate the stability of rupture-prone plaques and detect their locations. In this study, we hypothesize that heart rate (HR) is also one of the major factors that should be taken into account while mechanics of plaques is studied. We propose a tunable viscoelastic constitutive material model for the fibrous cap tissue in order to calculate the peak cap stress (PCS) in normal physiological (dynamic) conditions while HR changes from 60 bpm to 150 bpm in 2D plane stress models. A critical discussion on stress distribution in the fibrous cap area is made with respect to HR for the first time. Results strongly suggest the viscoelastic properties of the fibrous cap tissue and HR together play a major role in the estimation of the PCS values. The results of current study may provide a better understanding on the mechanics of vulnerable atherosclerotic plaques.

Keywords: Atherosclerotic plaque; Plaque vulnerability; Plaque Instability; Pulsatile flow; Finite Element Method; Viscoelasticity; Heart Rate

Introduction

Thrombus mediated ischemic cardiovascular events, such as acute myocardial infarction, are the major causes of mortality worldwide [1]. The rupture of vulnerable atherosclerotic plaques in the coronary and carotid arteries is responsible for a significant number of ischemic cardiovascular diseases and strokes, respectively [2,3]. Computational approaches have been extensively applied on two-dimensional (2D) or three-dimensional (3D) imaging modalities in order to estimate the peak cap stress in the fibrous cap area, known as peak cap stress (PCS), using mostly the finite element method (FEM) [4-9]. This evaluated PCS is compared to the "gold standard" of 300 kPa in order to determine the stability of rupture-prone plaques [5]. Plaque morphology, i.e., necrotic core size, fibrous cap thickness and so on, loading and boundary conditions, and plaque composition are significantly influential in PCS [5-9]. Constitutive material models applied in mechanical models of plaques have a wide range from simplistic, 2D linear and isotropic material models [10] to more sophisticated, 3D hyperelastic and anisotropic material models [6-9]. The problem with all of these material models is that none of them account for the viscous properties of the fibrous cap tissue, with the exception of our recent study [11]. It is well known that thin fibrous caps are severely inflamed and the percentage of macrophage density is as high as ~14% [1], which is even higher (>26%) for ruptured plaques. Since the fibrous cap tissue is thin, their ability to accommodate macrophages is very low. Also, apoptosis in the fibrous cap tissue is limited to macrophages alone. This is due to the amount of vascular smooth muscle cells (SMCs) decreasing to nothing throughout plaque progression until rupture occurs [12]. In other words, change in macrophages and SMCs density might lead to change in viscous properties of the fibrous cap tissue. Given the viscous nature of the thin fibrous cap area, heart rate (HR) is hypothesized to play a major role in assessing PCS. In this study, a tunable viscoelastic constitutive material model is proposed to computationally assess PCS in the fibrous cap tissue with respect to HR in a 2D computational platform. We developed a finite element platform which is solved by Mechanical APDL 2015 running on an Intel® Core^TM 2 Duo T6670 @ 2.2GHz and 2.00 GB of RAM.

Methods

Geometrical Model: Two groups of geometrical models are considered in this study:

a. Idealistic models as presented in Figure 1 [9,11], and

b. Realistic models obtained from varying imaging modalities, such as optical coherence tomography (OCT), intravascular ultrasound, (IVUS) and histology, [13] as shown in Figure 2. Two critical cap thicknesses are considered for idealistic models: 70 μm and 100 μm. The outer diameter of the coronary artery in all models is set to 3.3 mm [9,11].

Figure 1: Illustration of idealistic geometrical models used and the values of PCS calculated in this study. I1, I2, and I3 [10] are the 3 idealistic models, LV and HV refer to high and low viscous properties of the thin fibrous cap tissue, respectively. (a) shows the values of PCS for the idealistic models when cap thickness is set to 70 ìm, and (b) shows the values of PCS in the idealistic models when the cap thickness is set to 100 ìm. NC refers to Necrotic Core.

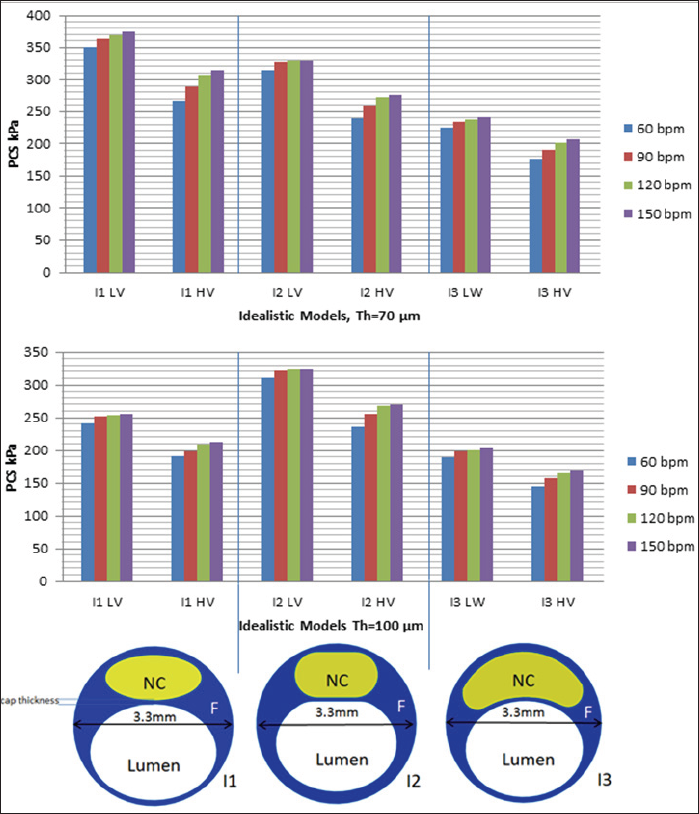
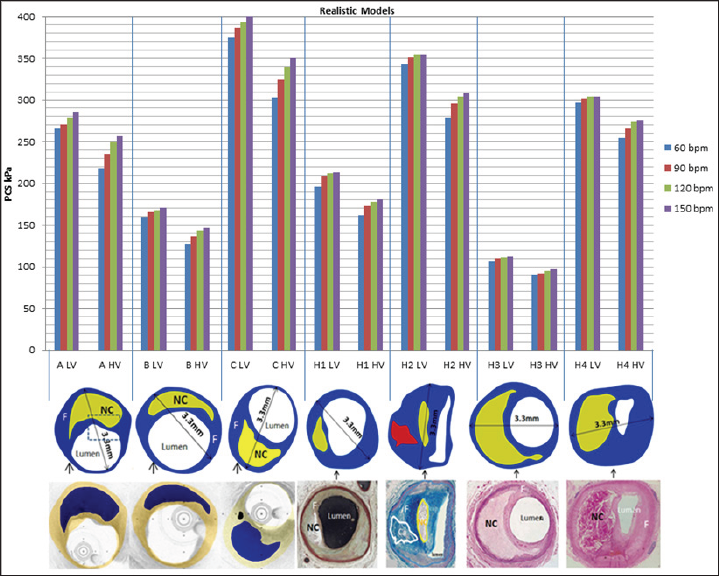
Figure 2: Illustration of patient-oriented geometrical models used in this study and their estimated PCS values through both HV and LV viscous materials; The imaging modalities used in this study are IVUS & OCT combined (models A, B, and C) and histology (models H1, H2, H3, and H4) [13, 17-19]. Blue, yellow and red in the digitized images refer to fibrous tissue, necrotic core and calcified regions, respectively.

Material Properties: Material models and the related modeling elements [14] is used to demonstrate the viscoelastic behavior of parameters for the fibrous cap tissue and necrotic core area used in this study are outlined in Table 1. The Prony series model with five elements [14] is used to demonstrate the viscoelastic behavior of the fibrous cap tissue [11], as outlined in Table 2.

Table 1: Mechanical properties of fibrous cap and necrotic core [6,14,15].

Table 2: Elements of time Prony series [16].

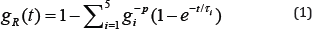
In order to study the effect of fibrous cap viscosity on the HR- induced PCS, two qualitative viscoelastic models are considered:

a. A low viscoelastic model, and

b. A high viscoelastic model. The elements of Table 2 are modified so that the new model can represent the mechanical behavior of the fibrous cap tissue with high viscosity, which is caused by the density of SMCs and monocytes inside the plaque.

To reach this end, relative modules are increased by 40% (see Table 3). This increase is based on the presence of foam cells, monocytes, etc., that provide viscous properties to the tissue. It should be noted that a lower viscoelastic behavior is closer in nature to an elastic or hyperelastic material model.

Table 3: Elements of time Prony series for plaque with low viscosity.

Boundary Conditions: Plaque outer wall is fixed in the radial and circumferential directions and a physiological, cyclic, and dynamic pressure is set as the lumen pressure for four different HRs of 60, 90, 120, and 150 bpm.

Numerical Procedure: FEM is employed in order to obtain the stress distribution and the PCS in the entire plaque section. The FE solver in this study is the commercially available FE code, ANSYS 2015. Geometrical models constructed in Solid Works 2015 are carefully meshed by triangular elements so that a fine mesh was used in the critical area, i.e., the thin fibrous cap tissue between necrotic core and lumen (Figure 2). A mesh independent study is then performed in order to ensure of independency of results obtained from the modeling inputs.

After creating mesh models, ANSYS was used to discretize the governing equations. To find unknown nodal displacements and forces, these equations are solved under plane strain assumptions by Mechanical APDL 2015 running on an Intel® Core™ 2 Duo T6670 @ 2.2GHz and 2.00 GB of RAM. It should be noted that the PCS values is considered the maximum value of von-Mises stresses calculated within the plaque for each condition [11].

Results and Discussion

Mesh Independency Study: Mesh independency of our results is of particular significance in this study which is done by performing further computation for each plaque model with higher mesh density. The mesh size is decreased until the point where by increasing the mesh density the results are not improved. The result of the mesh independency study is outlined in Table 4.

Table 4: Mesh independency study, the PCS for each model along with the number of elements used are shown in row A and B. In row B, models were meshed with more elements in comparison with models in row A. Results show an acceptable range for discrepancy of PCS in each plaque model; thus, the mesh models employed in row A are sufficiently precise to be used for our computational approach. Also, results are time dependent due to time-dependency of the material properties and pressure. In this pre-study, results of PCS at t=0.2s have been considered for this comparison. *S denotes the sphere-like models and *C the cylinderlike models.

Figure 1 shows the values of PCS in 3 idealistic models with respect to HRs of 60, 90, 120, and 150 bpm. Two thicknesses (70 μm and 100 μm) and two viscoelastic models (low and high viscosities) are considered for the fibrous cap tissue. Results clearly indicate that HR noticeably affects the values of PCS. Moving from 60 bpm to 150 bpm when the cap thickness is set to 70 μm and a low viscosity is assigned to the fibrous cap tissue, the range of change in the PCS for the same model is 15-25 kPa. This range widens to 35-45 kPa when a high viscosity is assigned to the fibrous cap tissue (Figure 1a). When the cap thickness is set to 100 μm, these ranges drop to 14-15 kPa for the low viscoelastic fibrous cap model and to 20-35 kPa for the high viscoelastic fibrous cap model (Figure 1b). For the high viscoelastic fibrous cap model, the rate of change in the PCS values are higher to that of the low viscoelastic fibrous cap model as HR increases, assuming all other conditions, i.e., cap thickness, lumen maximum pressure, etc., remain unchanged. Comparing the results outlined in Figures 1a & 1b, there is evidence that if a higher viscosity is assigned to the fibrous cap tissue, lower values (15%) for PCS are obtained.

For the idealistic models of I1 and I3, the values of PCS drop as the cap thickness is set from 70 μm to 100 μm for both high and low viscoelastic fibrous cap models. However, for the idealistic model of I2, regardless of the fibrous cap thickness (being 70 μm or 100 μm), the values of PCS remain in the same range with an error less than ~2%. Results obtained from I2 imply that the geometry of the plaque section and HR combined could be more influential on PCS than the thickness of the fibrous cap tissue alone.

The values of PCS under the same boundary conditions, i.e., dynamic lumen pressure and displacement boundary conditions, are shown in Figure 2 for realistic models. Results further reinforce the hypothesis developed using the idealistic models that if a higher viscosity is assigned to the fibrous cap tissue, the values of PCS drops by ~15% and the effect of HR on PCS is higher.?

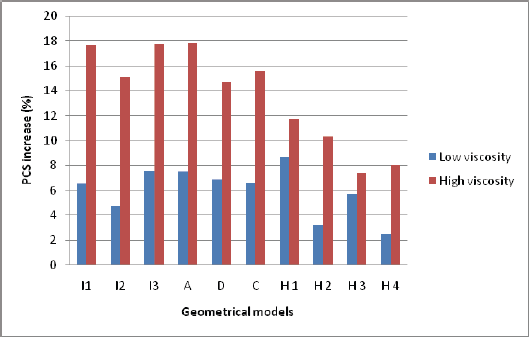
Figure 3 demonstrates the increase in PCS with respect to that of when HR=60 bpm discussed in Figs. 1 and 2 to better demonstrate the effect of viscoelasticity and HR on PCS. Results clearly show that jump in PCS from HR=90 bpm to HR=120 bpm is much higher than that of from 120 bpm to 150 bpm in both low and high viscoelastic models. Depending on the severity of viscous models applied and HR, the values of PCS increase from 2% (in which HR=90 bpm) to 18% (in which HR=150 bpm).

Figure 3: The comparison of values of PCS to that of obtained when HR=60 bpm for idealistic and patient-oriented models. Two thicknesses and two viscoelastic models are considered for the idealistic models (Figs. 3a and 3b), and all patient-oriented models (Fig. 3c). LV and HV refer to low and high viscoelastic model for the fibrous cap tissue, respectively.

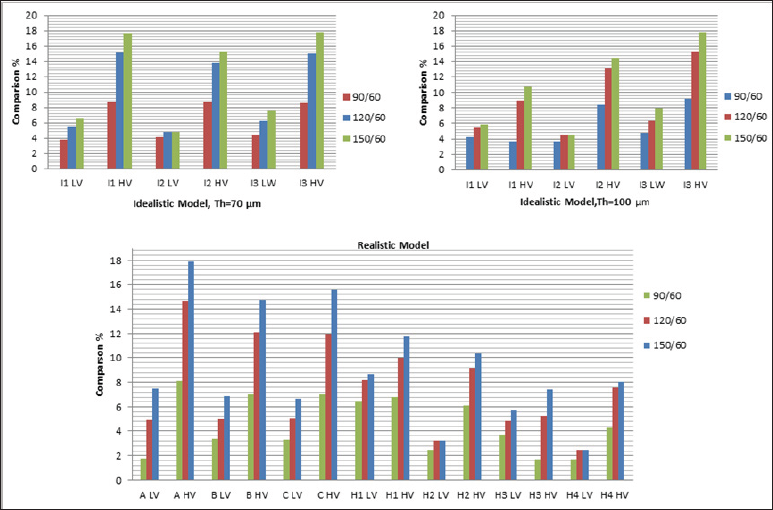
Figure 4: : Increase in PCS values due to degree of viscoelasticity of the fibrous cap tissue and HR. Blue bar shows the increase in PCS moving from elastic model to low viscoelastic model for the fibrous cap tissue when HR=60 bpm, red bar shows the increase in PCS moving from elastic model to high viscoelastic model for the fibrous cap tissue when HR=150 bpm.

Conclusion

To date, to the best of authors' knowledge, in the majority of the hemodynamics computational and experimental studies the modeling conditions are set based on a fixed HR of 72 bpm, which does not comprehensively represent the entire normal hemodynamic conditions. In resting status, sleeping status, etc., HR could be as low as 60 bpm. In contrast HR can increase to be as high as 150 bpm while jogging, running, etc. Also, daily emotional conditions, such as anxiety and stress, may affect the HR. Therefore, a HR range of 60-150 bpm seems to be reasonable normal HR conditions for cardiovascular related studies. In the current study, we show the significance of HR and viscoelastic material model of the fibrous cap tissue for the assessment of atherosclerotic plaque vulnerability by the estimation of PCS values within the plaque models. The fibrous cap tissue is known to be viscoelastic due to presence of SMCs, macrophages and collagen fibers. The degree of viscoelasticity, however, depends highly on plaque composition. Our results suggest that HR must be considered along with other factors such as cap thickness, NC size, etc., as a predictor for the instability of rupture-prone plaques. Results clearly show that that higher viscosity in the fibrous cap tissue can intensify the impact of HR on PCS values (see Figure 4).

Acknowledgement

The authors acknowledge the University of British Columbia and NSERC (Discovery Grant) for financial support.

Source of Funding: NSERC/Discovery Grant and University of British Columbia

References

1. Fuster V, Moreno P, Fayad Z, Corti R, Badimon J (2005) Atherothrombosis and high-risk plaque part I: Evolving concepts. Journal of the American College of Cardiology 46(6): 937-954.
2. Huang X, Yang C, Zheng J, Bach R, Muccigrosso D, Woodard P, Tang D (2014) Higher critical plaque wall stress in patients who died of coronary artery disease compared with those who died of other causes: A 3D FSI study based on ex vivo MRI of coronary plaques. Journal of Biomechanics 47(2): 432-437.
3. Casscells W, Naghavi M and Willerson J (2003) Vulnerable atherosclerotic plaque - A multifocal disease. Circulation 107(16): 2072-2075.
4. Akyildiz A, Speelman L, Nieuwstadt H, van Brummelen H, Virmani R, van der Lugt A, et al. (2015) The effects of plaque morphology and material properties on peak cap stress in human coronary arteries. Computer Methods In Biomechanics And Biomedical Engineering p. 1-9.
5. Ohayon J, Finet G, Gharib AM, Herzka DA, Tracqui P, et al. (2008) Necrotic core thickness and positive arterial remodeling index: Emergent biomechanical factors for evaluating the risk of plaque rupture. American Journal of Physiology - Heart and Circulatory Physiology 295(2): 717727.
6. Cilla M, Pena E, Martinez MA (2012) 3D computational parametric analysis of eccentric atheroma plaque: Influence of axial and circumferential residual stresses. Biomechanics and Modeling in Mechanobiology 11(7): 1001-1013.
7. Kiousis D, Rubinigg S, Auer M, Holzapfel G, Hallfasthetslara (Inst.), et al. (2009) A methodology to analyze changes in lipid core and calcification onto fibrous cap vulnerability: The human atherosclerotic carotid bifurcation as an illustratory example. Journal of Biomechanical Engineering-Transactions of the ASME 131(12): 121002.
8. Cardoso L, Kelly-Arnold A, Maldonado N, Laudier D, Weinbaum S (2014) Effect of tissue properties, shape and orientation of microcalcifications on vulnerable cap stability using different hyperelastic constitutive models. Journal of Biomechanics 47(4): 870-877.
9. Mohammadi H, Mequanint K (2014) Effect of stress intensity factor in evaluation of instability of atherosclerotic plaque. Journal of Mechanics in Medicine and Biology 14(5).
10. Veress AI, Cornhill JF, Powell KA, Herderick EE, Thomas JD (1993) Finite element modeling of atherosclerotic plaque. Paper presented at the pp. 791-794.
11. Zareh M, Fradet G, Naser G, Mohammadi H (2015) Are two-dimensional images sufficient to assess the atherosclerotic plaque vulnerability: a viscoelastic and anisotropic finite element model. Cardio Vasc Syst 3(1):
12. Hurst J (2011) 52. In Hurst's the heart (13^th edn.). McGraw-Hill Medical, New York, USA.
13. Fayad Z (2002) Computed Tomography and Magnetic Resonance Imaging for Noninvasive Coronary Angiography and Plaque Imaging: Current and Potential Future Concepts. Circulation 106(15): 2026-2034.
14. Heiland V, Forsell C, Roy J, Hedin U, Gasser T, et al. (2013) Identification of carotid plaque tissue properties using an experimental-numerical approach. Journal of the Mechanical Behavior of Biomedical Materials 27: 226-238.