Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2644-1403
Review Article(ISSN: 2644-1403) 
Physics of Anaesthesia Made Easy Volume 1 - Issue 2
Bhavna Gupta1* and Lalit Gupta2
- 1Department of Anaesthesia and Critical Care, AIIMS, India
- 2Department of Anaesthesia and Critical Care, Maulana Azad Medical College, India
Received: February 06, 2019; Published: February 28, 2019
Corresponding author: Bhavna Gupta, Department of Anaesthesia and Critical Care, AIIMS, Rishikesh, India
DOI: 10.32474/GJAPM.2019.01.000107
Abstract
Physics is an attempt to describe the fundamental laws of world around us. As anesthesiologists we deal with liquids and gases under pressure at varying temperature and volume. These inter relationships are simple, measurable and their understanding ensures a safe outcome for the patient. For the safe and efficient use of anesthesia apparatus, a basic knowledge of fundamental physics is must for a clear concept of their working principle. We have tried to simplify the basic physics related to anesthesia in a simplified way through the review article.
Introduction
Basic Concepts
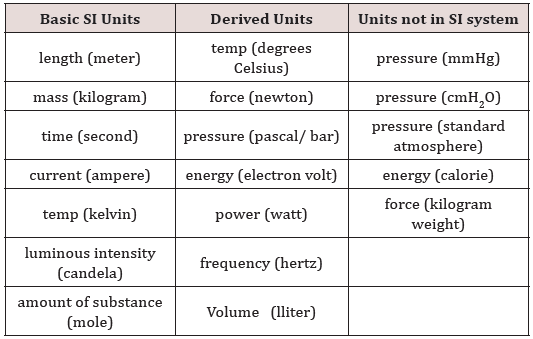
Units of Measurements
(Table 1)
Simple Mechanics
a) kilopascal = 7.5mmHg.
b) 1 Bar = 750mmHg
c) 1 kilopascal = 10.2cmH2O
d) 1 std atmosphere = 101.325kPa
e) 1 calorie = 4.18J
f) 1-kilogram weight = 9.8N
g) Pounds / inch2(PSI) -Atmospheric Pressure (1
PATM=14.7PSI)
h) 1 Bar = 100kPa = Atmospheric pressure at sea level [1].
Pressure
a) Force = mass x acceleration = kgms-2 = Newton
b) Pressure = Force/Area
c) 1 Pascal = I Newton acting over 1m2
Gauge pressure is defined as pressure which is measured when unknown pressure is measured relative to atmospheric pressure [2]. This pressure is used in measuring:
a) Blood pressure
b) Airway measurements
In order for fluid to pass out of the barrel of the syringe the same pressure must be developed in the syringe.
a) For a 20ml syringe (diameter 2cm) – pressure generated is 100kPa; even this is 6 times more than SBP of 16kPa (120 mmHg). So, during Biers block, pressure in the vein during rapid injection can exceed systolic pressure, particularly if a vein adjacent to the cuff is present.
Bed Sores: for a 20kg of patient mass supported on an area of contact of 100cm2 (10x10)
a) Force = 196N (20kg x 9.81); Pressure = 19.6kPa
b) Normal SBP = 16kPa, so there is always a risk of Ischemia
Similar concepts are applied for pressure relief valves and expiratory valves of anaesthetic breathing systems. Pressure in the circuit exerts a force on the diaphragm and when this force is greater that the force exerted by the valve, air escapes through the expiratory valve. They are typically low-pressure valves (50Pa).
Fluid Mechanics
Flow is defined as amount of fluid or gas passing in unit time. Flow becomes laminar to turbulent after Reynold number (defined below) reaches above a value of 2000.
Reynold’s number (Re): - is a dimensionless number and has no units and is defined as:
Velocity x pressure x density / viscosity
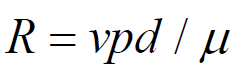
When
Re < 2000 – flow is laminar
Re > 2000 – flow is turbulent
2.4. Points to Remember
a) Viscosity is an important parameter to determine laminar
flow
b) Density is an important parameter to determine turbulent
flow
c) Reynold’s number of 2000 delineates laminar from turbulent
flow.
Laminar Flow
Flow moves in a steady state with no turbulence or eddies. Flow is greatest in the mid center and zero in peripheral wall. Hagen Poiseuille Equation is used to determine laminar flow, defined as:
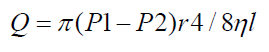
Where P1 – P2 = Pressure difference across the tube
r4 = Radius to the power of four
= Viscosity
L = Length and 8 = constant
Clinical Relevance
a) The endotracheal tube with size 7 has almost twice resistance as compared to sized 8.0 ETT
b) Intravenous fluids: Intravenous fluids flow via laminar flow, and flow is determined by Hagen Poiseuille Equation. This means that flow is greater through a shorter and wider cannula as compared to cannula which are long and small when the same pressure is applied to it. That’s why shorter and wider cannula such as 16 or 18 G cannulas are preferred during resuscitation.
Turbulent Flow
Turbulent flow denotes a situation in which the fluid flows in an unpredictable manner with multiple eddy currents which are not parallel to the sides of the tube through which they are flowing. Flow is facilitated by irregularities, sharp angulation, corners and are predicted by density of gas. Reynold number is always greater than 2000.
Clinical Relevance
a) Kinked ETT or ETT connectors often result in turbulent flow.
b) Heliox (a mixture of 21% helium and 79% oxygen) is used
to reduce density and thereby improve the flow and is used in
respiratory tract obstruction. Helium is much less dense than
nitrogen, which constitutes 79% concentration of air. In patients
with upper airway obstruction, flow is through an orifice and hence
more likely to be turbulent and dependent on the density of the gas
passing through it. Therefore for a given pressure gradient (patient
effort), there will be a greater flow of a low density gas (heliox) than
a higher density gas (air).
c) There is laminar flow during quiet breathing which becomes
turbulent during coughing and speaking thereby resulting in
breathlessness or dyspnea.
d) According to, Hagen – Poiseuille’s Law. flow is laminar at low
flows in the flow meter, while at higher flows, the law applicable to
turbulent flow is applicable [3].
Critical Flow
Critical flow for a typical anesthetic gas has approximately the
same numerical value as the diameter of the airway concerned.
a) 9mm ETT has a critical flow of 9L/min: Above 9L/min =
turbulent flow
b) Air has a lower density than Nitrous Oxide – laminar flow
prevails
c) Air flow through the smaller airways is slower – laminar
flow predominates
The Gas Laws
a) Boyles Law
b) Charles Law
c) Third Perfect Gas Law
d) Dalton’s Law of Partial Pressures
e) Universal Gas Constant
Boyles law: Boyle’s law is a gas law, stating that the pressure and volume of a gas have an inverse relationship, when temperature is held constant.
PV = k
(P = pressure, V = volume, and k = constant)
Cylinder capacity of oxygen cylinder at atmospheric pressure
= 10 L
Absolute cylinder pressure= 138 bar
Therefore, since,
P1V1 = P2V2
138x10 = 1xV2
So, V2 = 1380 L
Charles Law (Gay Lussacs Law):
a) Charles Law States that at Constant Pressure
V a Temp (i.e. Gases expand when heated)
Clinical relevance- respiratory gas measurements are done at ambient temperature while exchange of gases rakes place at room temperature i.e. 37 ºC
b) Third Perfect Gas Law
At constant volume, absolute pressure of a mass of gas varies directly with temperature.
P α Temp
Clinical Relevance
a) Medical gases are stored in cylinders having a constant
volume and high pressures (138 Barr in a full oxygen/air cylinder).
If these are stored at high temperatures, pressures will raise
causing explosions.
b) Adiabatic changes: it is a change which doesn’t involve
transfer of heat (Q) or matter into and out of a system, so that Q = 0,
and such a system is said to be adiabatically isolated.
Clinical Relevance: When a valve of an oxygen cylinder is opened suddenly, oxygen will rush into high pressure hose or stem of oxygen regulator and on reaching the end of hose, adiabatic process might occur. That suggests that local pressure is much higher than that of filling pressure of the cylinder (about 150 bar) for a very brief time. The process is adiabetic because compression occurs without any heat from outside and the effect can lead to sudden explosion if there is dust or grease at regulator preventing further gaseous expansion.
Dalton’s Law of Partial Pressures: It states that in a mixture of gases, the pressure exerted by each gas is the same as that which it would exert if it alone occupied the container
Universal Gas Constant: Ideal Gas law is deduced by combining all 3 perfect gas laws and combining with the avogadro’s hypothesis the concept of mole gives us the Universal Gas Constant = R.
Where R = Universal Gas Constant
n = Number of moles
Avogadro’s Hypothesis: States that equal volumes of gases at the same temp and pressure contain equal number of molecules. One mole of any gas occupies 22.4L at STP (standard temperature and pressure). Avogadro’s number is defined as the number of elementary particles (molecules, atoms, compounds, etc.) per mole of a substance. It is equal to 6.022×1023 mol-1 and is expressed as the symbol NA.
Clinical Relevance
Nitrous oxide cylinder contains 3.4kg N2O
Mol wt. of N2O = 44 (1mole)
1 mole occupies 22.4 L at standard temp and pressure
Therefore 3400 g occupies 22.4 x 3400/44 = 1730L
Solubility Mechanics
Solubility Saturated vapor pressure is defined as the partial pressure exerted by vapour in the equilibrium state is achieved at the surface between vapor of the liquid and liquid itself when a liquid is placed in a closed container. SVP is associated with Henry’s law [4].
Henry’s Law states that at a temp, the amount of a given gas dissolved in a given liquid is directly proportional to the partial pressure of the gas in equilibrium with the liquid.
a) Bubbles may be seen when a liquid is warmed and less gas dissolves in it.
b) The effect of high pressure is particularly relevant to deep sea divers as the solubility of nitrogen if breathed under pressure passes into solution in the tissues. If a return to atmospheric pressure is made too rapidly, the nitrogen comes out of solution as small bubbles in the joints and tissues causing pain and bends.
Ostwald Solubility Coefficient is the volume of gas which dissolves in one-unit volume of the liquid at the temp concerned (Independent of pressure) Ostwald solubility coefficient of ether is highest, and the value is 12. Halothane has solubility coefficient of 2.3 and that of nitrous oxide is 0.47. So, ether used to be carried away very slowly and its concentration to build up in alveoli was very slow thereby leading to slower induction of anesthesia.
Blood: Gas Solubility Coefficient: the ratio of the amount of substance in equal volume phases of blood and gas in a closed system at equilibrium and at standard temperature and pressure.
Oil: Gas Solubility Coefficient: the ratio of the amount of substance present in equal volume phases of oil and gas in a closed system at equilibrium and at standard temperature and pressure.
Clinical Relevance: Agents with the highest oil solubility have the greatest potency and lower MAC value and forms the basics of Meyer Overton theory of anesthesia Table 2.
Diffusion: Diffusion is a process in which the molecules of a substance (such as gas) transfer through a layer such as the surface of a solution to another one.
Grahams Law states that the rate of diffusion of a gas is inversely proportional to the square root of its molecular weight.
Clinical Relevance
a) Thus, heavier gas will diffuse more slowly. Also, if the MW
(molecular weight) of a gas is four times of another, it would diffuse
at half the rate of the other.
b) Local anesthetics injection for nerve block should be done as
proximity to the nerve as diffusion only allows limited penetration
of the LA into the tissues.
c) Heliox mixture of helium and oxygen, is a lighter gas, hence is
used in airway obstruction to improve diffusion and gas exchange
Fick’s Law of Diffusion:
The rate of diffusion of a gas across a membrane is directly proportional to the membrane area (A) and the concentration gradient (C1-C2) across the membrane and inversely proportional to its thickness (D).
Rate of diffusion α A (C1-C2) / D.
Clinical Relevance
a) Anesthetic vapors diffuse into breathing circuits and later
acting as Vaporizers at the time of discontinuation of anesthetic
gases.
b) N2O gas diffuses into cuff of endotracheal tube.
c) Diffusion of N2O into air filled cavities as in pneumoecephalous,
pneoumoperitoneum etc.
Concentration Effect and Second Gas Effect: At the time of inspiration, Nitrous oxide is absorbed into blood stream at a faster rate than oxygen or nitrogen gas. At the peak of inspiration, when pressure in the alveoli equalizes with the ambient pressure, there is net surpulous supply of oxygen and nitrogen molecules. This results in effects known as the “concentration effect” and the second gas effect. When a constant concentration of an anesthetic such as sevoflurane is inspired with nitrous oxide, the alveolar concentration of sevoflurane is accelerated due to nitrous oxide, because alveolar uptake of the latter creates a potential sub atmospheric intrapulmonary pressure that leads to increased tracheal inflow.
Diffusion Hypoxia: Nitrous oxide diffuses faster from the alveoli at the end of anesthetic exposure, as N20 diffuses faster into the alveoli thereby diluting the gases leading to fall in oxygen saturation, also known as diffusion hypoxia, therefore 100% oxygen is required at the end of surgery to avoid diffusion hypoxia.
Osmolarity
It is defined as the sum total of the molarities of the solutes in
a solution.
a) Ringer Lactate has an osmolarity of 278mosm/l
Constituents of RL
Na 131mosm/l
K 5mosm/l
Cl 111mosm/l
Ca 2mosm/l
Lactate 29mosm/l
Plasma has an osmolarity of 275–295 mosm/kg >99% due to
Na, Cl, HCO3.
Energy Mechanics
Heat Capacity: Heat Capacity is defined as the amount of heat required to raise the temperature of a given object by 1 kelvin.
Specific Heat Capacity
Specific Heat Capacity defined as the amount of heat required to raise the temperature of 1kg of a substance by 1 kelvin. (J /kg/ Kelvin)
Clinical Relevance
Normal body temperature is 36 degrees Celsius and basal heat production is 80 W(J/Sec)
Shivering increases heat production by 4fold (ie 320W, with extra 240W= 14.4kJ/min) 245kJ needed to increase temp by 1 degree (total heat capacity = 3.5x70kg), so patient has to shiver for approximately 245/14.4=17min to produce this extra heat.
Bernoulli’s Principle
It is defined by the law of conservation of energy. Flowing liquid possess 2 types of enrgy- potential and kinetic energy. If there is a constriction in tube, there is increase in kinetic energy, there is subsequent fall in potential energy, to conserve the total energy [4].
The Venturi Effect
Venturi effect was named after famous Italian physicist, Giovanni Battista Venturi (1746–1822). It is the effect by which the introduction of a constriction to fluid flow within a tube causes the velocity of the fluid to increase, therefore, the pressure of the fluid to fall. By measuring the change in pressure, the flow rate can be determined, as in various flow measurement devices such as venturi masks, venturi nozzles and orifice plates.
a) The Venturi effect may be observed or used in the following:
b) The capillaries of the human circulatory system, where it
indicates aortic regurgitation.
c) Injectors used to add chlorine gas to water treatment
chlorination systems.
d) Ventilators.
Conada effect
If a constriction occurs at bifurcation because of increase in
velocity and reduction in the pressure, fluid (air, blood tends to
stick to one side of the branch causing maldistribution.
a) Mucus plug at the branching of tracheo-bronchial tree may
cause maldistribution of respiratory gases.
b) Unequal flow may result because of atherosclerotic plaques
in the vascular tree.
c) Fluid logic used in ventilators employs this principle to
replace valves or mobile parts.
Spectrophotometry– Basic Concepts
a) Beers Law
Beer law states that amount of light absorbed is proportional to the concentration of the light absorbing substance.
b) Lamberts Law
Equal thicknesses absorb equal amounts of radiation. Amount of light absorbed is proportional to the length of the path that the light has to travel in the absorbing substance. Both laws say that the absorption of radiation depends on the amount of a particular substance. This fact has been utilized in pulse oximetry.
Pulse Oximetry: It involves Spectrophotometry & Plethysmography.
a) Light absorbed by the blood depends on the quantities of
Haemoglobin and Deoxy-Hb and the wavelengths of the light.
Absorbance of Oxy-Hb at wavelengths of 660 nm (red light) is less
and that of DeOxy-Hb is less in 940nm (blue light).
b) Two diodes, one emitting red light 660 nm and the other
a blue light (940nm) are positioned so that they are opposite
their respective detectors through 5-10 mm of tissue. The output
processed electronically on the other side of the finger gives the
oxygen saturation depending on the relative amount of each type of
Hb present in the pulsating arterial blood.
c) More the Hb per unit area more is the light is absorbed. This
property is described in a law in physics called “Beer’s Law”. While,
longer the path the light has to travel, more is the light absorbed.
This property is described in a law in physics called “Lambert’s Law.
Capnography and Anesthetic Analyzers
a) Both mainstream and side stream capnometers rely on
absorption spectroscopy and, accordingly, on Beer-Lambert law.
b) In side stream type infrared absorption spectroscopy,
respiratory gas analyzers are usually integrated in the anesthesia
machine. These devices use different wavelengths appropriately
chosen to measure, in addition to pCO2, the concentration of other
respiratory gases such as nitrous oxide, and different volatile
anesthetics (anesthetic analyzers) [5].
Circulation
Hemodynamics can be defined as the physical factors that govern blood flow. These are the same physical factors that govern the flow of any fluid and are based on a fundamental law of physics.
Ohm’s Law
a) Pressure = Flow x Resistance
b) Voltage = Current x Resistance
c) Resistance = Pressure/Flow
Law of Laplace
Tension may be defined as the internal force generated by a
structure, La Place Law states that for cylinders,
T = Pr
(where T = wall tension, P = pressure of fluid within the cylinder,
r = radius
Ohm’s Law: It states that current (I) equals the voltage difference (ΔV) divided by resistance (R). In relating Ohm’s Law to fluid flow, the voltage difference is the pressure difference (ΔP; sometimes called driving pressure, perfusion pressure, or pressure gradient), the resistance is the resistance to flow (R) offered by the blood vessel and its interactions with the flowing blood, and the current is the blood flow (F). This hemodynamic relationship can be summarized by:
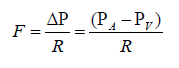
a) For the flow of blood in a blood vessel, the ΔP is the pressure difference between any two points along a given length of the vessel. When describing the flow of blood for an organ, the pressure difference is generally expressed as the difference between the arterial pressure (PA) and venous pressure (PV).
Law of Laplace (Wall Stress):
Laplace Law states that for cylinders,
T = Pr or P =T/r (e.g. Arteries)
For sphere,
P= 2T/r (e.g. Anesthesia Bag/ Heart)
(Where T = wall tension, P = pressure of fluid within the
cylinder/ sphere, r = radius);
Tension may be defined as the internal force generated by a
structure.
Clinical Relevance
a) In a failing heart –there is an increase in radius therefore a
decrease in pressure, and failing heart is unable to increase T.
b) In a normal heart, increase in radius is beacuase of increase
in venous return, also there is increase in Tension according to
Frank starling law. Therefore there is no change in pressure.
c) The management of stable angina is to reduce wall stress
thereby decreasing myocardial oxygen demand.
d) In a patient with chronic hypertension, there is overall
increase in left ventricular wall thickness to compensate for
increased wall stress.
e) Left ventricular pressure increases with symptoms of
increased “afterload” of the heart, including systemic hypertension
and aortic valve stenosis.
Miscellaneous Physics
Archimedes’ Principle
Archimedes’ principle is a law of physics fundamental to fluid mechanics. It says any object, wholly or partially immersed in a stationary fluid, is buoyed up by a force equal to the weight of the fluid displaced by the object.
a) Air Bubbles: According to Archimedes’ principle, air bubbles
always tend to go upward in any liquid, including saline, drugs, and
blood. So, just keep up the cone of the syringe (exit path), bubbles
can be removed by ejecting air by pushing the plunger of syringe.
b) Cardiac Surgery: During cardiac surgery, de-airing is
done before aortic de-clamping in order to prevent air bubbles
from reaching the brain. If de-airing is performed through a
ventriculotomy, the anesthesiologist is asked to place the patient in
the Trendelenburg position, so that the venting site is located above
and air expulsion is favored.
c) Archimedes’ principle helps cardiac anesthesiologists to
prevent (or reduce) cerebral air embolism when air accidentally
enters the circuits during cardiopulmonary bypass (CPB) by
immediately placing the patient in steep Trendelenburg position.
Calculating the Duration of a N2O Cylinder
Just Now a new N2O cylinder is fitted to the Machine. How Long Will It Last…? Can a case of 6 hrs duration be taken with this cylinder?
First step is to calculate the Amount of N2O Gas in Cylinder?
a) Atomic weight of nitrogen – 14, oxygen – 16,
Molecular weight of N2O = 14+14+16 = 44
b) As per AVAGADRO Hypothesis:
one-gram molecular weight of all gases will contain the same
number of molecules and occupy the same volume (22.4 l) at STP.
So,
32g of O2 = 44 g of N2O = 28g of N2 =22.4Lt.
Empty weight of the cylinder = 12.5 Kg, Cylinder weight with
N2O = 15 Kg
So,
Weight of the N2O = 2.5Kg = 2500g; 44g of N2O = 22.4Lt
(Avogadro hypothesis)
Therefore 2500g = 22.4/44 x 2500 = 1272Lt.
So, amount of duration for which a N2O cylinder can be used =
1272Lt/ flow of N2O on machine per minute.
(Suppose the flow of N2O is 3Lt/m=180Lt/hr, so the cylinder
will last for 1272/180= 07hr).
Unexpected Help from the Reservoir Bag
The reservoir bag in an anesthesia machine allows manual ventilation as well as a “visual” monitoring of spontaneous breathing.
a) Thanks to Laplace’s law, it can prevent barotrauma in case
of malfunction or unintentional closing of the APL (adjustable
pressure limiting) valve. In fact, in the presence of an overflow or a
flow obstruction in the breathing system, the radius of the reservoir
bag increases (Figure 5) and, according to Laplace’s law, the
pressure inside it decreases (P=2T/R), thus preventing a dangerous
rise in pressure in the entire breathing system and, consequently,
in lungs.
b) Accordingly, a reservoir bag which feels stiff should be
replaced, since its wall tension (which we can define, similarly to
surface tension γ, as the work required to extend the surface of an elastic membrane by a unit area will be higher, for the same radius
(or its radius will increase by a lesser extent for the same value of
wall tension), thus providing a lower “pressure relief”.
Conclusion
Anesthesia has evolved very fast over last few decades but the basic are still same and applicable in day to day anesthesia instruments and apparatus. It is necessary to understand the basic physics behind every anesthetic instrument, so that it becomes easy to operate. Learning conceptual physics also helps to trouble shoot the problem associated with them.
References

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...