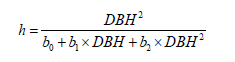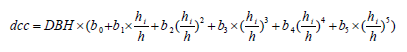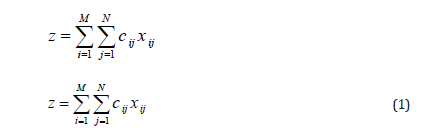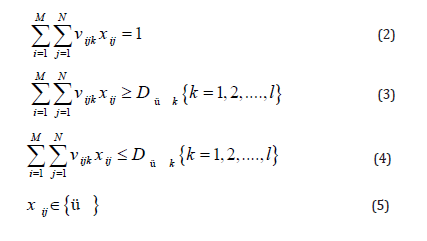A New Construction Heuristic by Parts to Optimize the Forest Assortment Volume 7 - Issue 1

Rodrigo Freitas Silva¹*, Marcelo Otone Aguiar¹, Mayra Luiza Marques da Silva² and Gilson Fernandes da Silva³

• ¹Department of Computing Alegre, Brazil
• ²Department of Agrarian Sciences, Sete Lagoas, MG, Brazil
• ³Department of Forest Engineering, Jerônimo Monteiro, ES, Brazil

Received: June 14, 2019;   Published: June 25, 2019

Corresponding author: Rodrigo Freitas Silva, Department of Computing, CCENS, Alegre-ES, Brazil

DOI: 10.32474/CIACR.2019.07.000253

Abstract PDF

Abstract

The tree bucking optimization problem is to determine the optimum cutting pattern of the trees stem in order to maximize their commercial value. The cut pattern depends on the products that are marketed and the characteristics of each tree harvested. This work proposes a new heuristic designed to optimize the assortment of trees during harvesting. The performance of this method was compared to the results obtained in the literature for the meta-heuristics Simulated Annealing and Genetic Algorithm. It was concluded that the proposed heuristic is effective because it generated the best results when compared to the other solution methods.

Keywords: Multiproducts; Optimization; Bucking; Tree Bucking Optimization Problem

Introduction

The demand for forest multiproducts has been increasing in the international and Brazilian market, serving as justification for a previous evaluation of the forest assortment. This evaluation depends, among other factors, on the management plan to which the forest was submitted, aligning the needs of the consumer market with the objective of maximizing the revenue from harvested timber [1,2]. Forest plantations usually have their production directed only at a particular type of product, aimed at supplying a specific industry. However, forests often produce a greater variety of products, useful for, for example, laminating, sawmill and pulp, where there is not always a close demand to give them some kind of value [3]. Forest assortment is the term used to qualify and quantify the tradable wood stock in the forest, based on a list of multiple marketed products, and constitutes a tool for making decisions related to forest management [4,5]. The tree bucking optimization problem is to determine the sequence of products (logs) that must be obtained from a particular stem in order to maximize its revenue. The products can be the same or different from each other [6]. At stem-level, the cut pattern that maximizes the stem value should be determined [7]. Researches in search of optimum assortment solutions, faced with a combinatorial explosion with several cut alternatives, are part of a specific category of problems known as the Cutting and Packing Problem [8]. The difficulty in finding the optimum assortments is due to the exponential growth of the number of cutting patterns to be analyzed in function of the number of products marketed and the tree measurements.

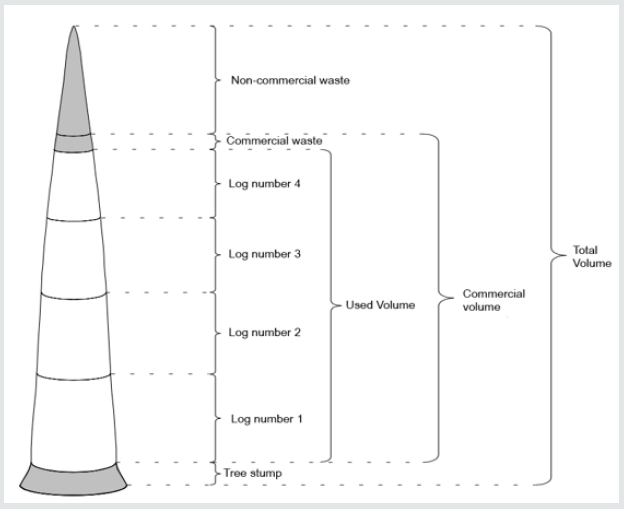
For example, some volumes and residues defined at stem-level are shown in Figure 1. The stump is a non-commercial residue commonly measuring 0.1 meter. Then, from the base towards the top, 4 logs of unspecified lengths and diameters are removed from a set of possible alternatives. The types of products extracted will depend the multiproducts considered for commercialization. In the sequence, it is possible to verify a commercially viable residue, not used, however, due to the choice of the assortment adopted. Therefore, the commercial residue is not long enough to form a new log and could not be added to the already extracted log. Finally, there is another non-commercial residue that is the tip of the tree. Given the problem, classified in a general class of problems called NP-hard, and given the computational constraints for an exhaustive search for an optimal cut pattern, new heuristic solution methods have been proposed in the literature with the objective of maximizing the tree value [9]. The main objective of this work is to propose a new solution method for the stem-level optimum bucking problem named Construction Heuristic by Parts (CHP). This method, considered partially greedy and partially random, aims to select the most profitable cutting alternative in a forest stand of Pinus taeda L. Its performance was compared to the income obtained by the company, whose assortment is determined by the experience of the chainsaw operator, and the Simulated Annealing and Genetic Algorithm meta-heuristics results, if they had been used, whose results have been found already published in the literature.

Materials and Methods

Study Area

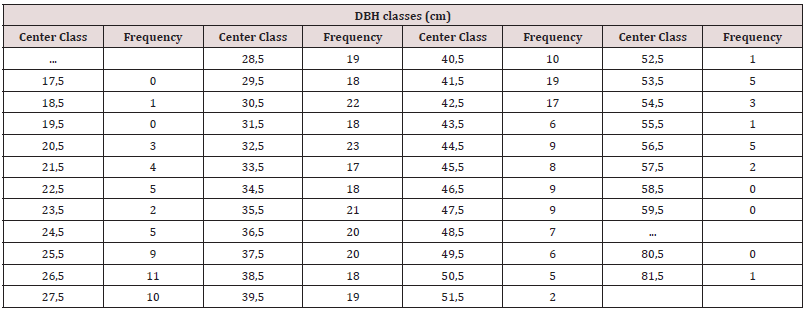
The data used in this study were obtained from 10. They come from the Southern Region of Brazil, Correia Pinto city, Santa Catarina state, property of the Klabin Industries. Were analyzed 11.5 hectares of Pinus taeda L. planted in 1978 at Capela I farm. In total, 453 trees were found in the demarcated study area, which 408 were harvested and 31 of them were cubed. The purpose was to build the hypsometric relation and the taper function to estimate the commercial heights and the volumes at individual tree level. The classes of diameter of the studied forest stand are presented in Table 1. The Simulated Annealing and Genetic Algorithm meta-heuristics were used by 10 to generate, by diameter class, assortments of Pinus taeda L. forest stand. According to the author, the choice of the approximate algorithms was due to the long execution time of the exact algorithms, given the wide variety of commercially acceptable products. The results were compared to the average yield of the harvest data obtained by the company, whose assortment was manually chosen by the chainsaw operator. The author concluded that the Genetic Algorithm and Simulated Annealing would be 9.55% and 7.85% more profitable, respectively, if they had been used to determine the assortments of the trees harvested. The models necessary to estimate the total height of the trees and its diameters along the stem were provided by the company, already adjusted, and their respective equations were:

Hypsometric Relation

Where:

h = total height (meter);

DBH = diameter measured at 1.3 meter above ground (cm);

b₀ = 7,19827; b₁ = -0,24839 and b₂ = 0,03447.

Where:

dcc = diameter with bark along the stem (cm);

h_i = cutting height (m);

h = total height (m);

(h_i /h) = relative height (m);

DBH = diameter measured at 1.3 meter above ground (cm);

b₀ = 1,19837; b₁ = -4,87173; b₂ = 22,56860; b₃ = -50,29490; b₄ = 50,20750 and b₅ = -19,00690.

Multiproducts

The products marketed by the company, by use class, are presented in Table 2. The logs can be sent to sawmill, sold or used for pulp production. In total, 42 different products can be marketed. Let the NPC be the potential number of cutting patterns, L the number of different products considered and T the maximum number of logs that can be cut from the tree, depending on the useful height and the lengths of each product. Thus, we have that NPC = LT [4].

Integer Linear Programming Model

The formulation of the integer linear programming model base of this study is presented below [11]:

Maximize

Subject to:

Brief description of the model variables:

Z = tree total value (US$);

x_ij = decision variable, j-th cut pattern for i-th diameter class;

c_i,j = value of each i class of diameter, following the j cutting alternative;

m = total number of diameter classes;

n = total number of cutting alternatives for the i-th diameter class;

V_i,j = volume (m³) produced by diameter class, k product, by the i-th diameter class, adopting the j-th cutting alternative;

D_minK e D_maxK = minimum and maximum volumetric demands (m³) of each k product.

The objective function (1) represents the maximization of the trees revenue given the selected cutting pattern. The constraints of diameter class (2) and (5) guarantee the choice of a single j cutting alternative for a i class of diameter. Finally, the demand constraints (3) and (4) impose volume limits per marketed product.

Solution Method: Construction Heuristic By Parts (CHP)

The proposed heuristic consists of an iterative procedure of construction and selection of the best cutting pattern made in two constructive phases. Firstly, several solutions are built using greedy strategy and the best of them is selected. Then, in the second phase, the final part of the selected solution is ignored and reconstructed using randomness. During the first stage of construction of the solution, from the tree stem base, it is verified which are the different products candidates that can be extracted initially, given its length restrictions, the small-diameter tip and the tree characteristics. Then, for all candidate products to be extracted, only thenmost profitable products are selected to be evaluated and later processed by the heuristic. For each of these n products initially selected, each cut is individually simulated starting n different assortments. With the rest of the tree stem, for each of the nth assortments initiated, the cut of the second log is evaluated in the sequence. It is then evaluated again which are the nextnbest products to be extracted from the stem, simulating the cut of each of them, in order to obtain, thus, n² different assortments. In this way, the process continues until no more commercially viable logs can be extracted from the rest of the tree. At the end, n^T different solutions are obtained from the combination of thenmost valuable logs that could be harvested in each part of the tree, where T is the maximum number of logs that can be removed from the respective tree. Then, the most profitable assortment is selected as the initial greedy solution of the CHP. It is important to note that a very large value attributed tonwould imply the transformation of this initial procedure into another equivalent of brute force, making it impossible to execute the heuristic, given the existence of 42 different products possible of commercialization.

The second phase of the algorithm uses randomness to reconstruct the final part of the solution selected in the first phase. Considering the initial choice of the solution obtained, the CHP keeps the first part of this solution unchanged and eliminates the rest of the solution. This first part of the solution consists of consecutivexlogs kept unchanged from the base towards the tip of the tree. The final part of this solution is rebuilt through the random cutting of new products until it is no longer possible to extract more products from the rest of the tree, generating, therefore, a new solution. If this new solution is better than the initial one, it will then be stored; otherwise, it will be discarded. The system only stores the best solutions found. The second part of the heuristic is executedktimes. Therefore, the final part of the solution obtained in the first phase of the CHP is reconstructedktimes, potentially generatingknew solutions, all with the samexfirst logs. In this case, the established stop criterion for CHP is the number of times (k) that the second phase of this algorithm will be executed. In this heuristic, the solution obtained in a greedy way in the first phase of the algorithm is inserted simply as an initial estimate for the CHP. Then, the final part of this solution is reconstructed using randomness in the search for new admissible products in each part of the trunk tree. The intention is that one change lead to another, and in the end, maximize the income of the tree analyzed by reducing the commercial waste.

Results and Discussion

*where: US$ 1.00 = R$ 3.86

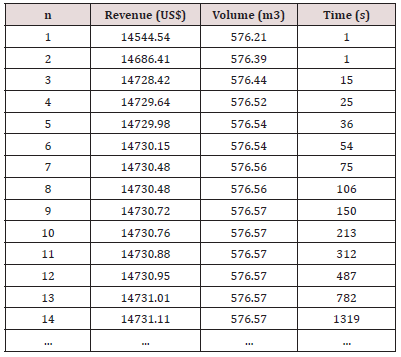
The CHP was initially parameterized to find the most valuable cut pattern. Therefore, a correct configuration of its parameters can achieve greater financial profitability without loss of efficiency, which would prove the benefits of its use. At first, the CHP first phase was investigated, responsible for generating an initial solution to the problem. The Table 3 shows the results of the simulations of this analysis, alternating in each simulation the quantity of the most profitable products (n) measured in each part of the stem, all of them combinatorially evaluated to produce a better assortment. In addition, it is important to mention that the total revenues and the total volumes shown in this table are the results of the sum of all revenues and of all volumes mensured, calculated for each of the class centers analyzed. The results indicate that, as the number of candidate products (n) evaluated increases, the incomes and volumes obtained naturally improve, although this also impairs the efficiency of the algorithm because the simulation time growing considerably. Although there are 42 distinct products, it is computationally delayed to perform tests for a very large n, explained by the exponential growth of the combinations number to be evaluated. In order for CHP not to be inefficient when compared to other methods implemented in the literature, it was decided to choose an n equal to 4 to continue the execution of this algorithm. It is also important to highlight that, regardless of the next random searches to be made, the final solution will never be less than US$ 14729.64. The next scenario analyzed was the algorithm stopping criterion, that is, the number of times that CHP second phase will be executed (k), possibly generating k new solutions. The number of logs kept unchanged from the initial solution (x) was also analyzed. 10 simulation were performed for each configuration of the parameters k and x, obtaining a coefficient of variation smaller than 0.01%. The (Table 4) shows the results of assortment simulations.

*where: US$ 1.00 = R$ 3.86

Given the results found, the configuration selected to parameterize the CHP was x = 4 and k = 1000. With these values the algorithm was able to generate good solutions in a short period of time. The volumes were not informed because they were practically the same 576,57 m3 in most of the results, evidencing, from a certain point, the importance of the assortment to obtain greater profitability. The optimization results were compared to those obtained by [10] using the Genetic Algorithm and Simulated Annealing metaheuristics in the same case study. In addition, the data from the field records were considered to estimate the average income of the harvest obtained by the company. Table 5 presents a summary of the data already published in the literature and the results of the simulations obtained through the CHP solution method. Analisando os resultados obtidos (Table 5), pode-observes that, todos os metodos avaliados, a CHP apresentou as melhores receitas. The CHP Tivesse sido executado com 1000 iterações, received media obtida era from US $ 14730.99. Comparado com has given the media a rating of 10.22%. It is said that CHP is 0.61% but is only 2.2% Algoritmo Genético, but only Simulated Annealing. It can also be observed that CHP was able to maximize revenue by up to US$ 14731.48 (k = 100000). It was evident that the choice of the stopping criterion makes a difference in relation to the results obtained. The greater the number of new solutions processed, the greater the revenue obtained, although this also implies in the loss of algorithm efficiency. Using the CPLX, it was verified that the optimal solution of the problem provides a revenue of US$ 14732.07. Therefore, the solution obtained through the CHP reached 99.99% of the optimal solution.

*where: US$ 1.00 = R$ 3.86.

Conclusion

This paper proposes an alternative heuristic to determine the optimum bucking for each stem in a way that maximizes the total stem value. It was found that for a better CHP performance, the number of products to be evaluated in each part of the stem should be 4. The amount of logs kept unchanged in the heuristics first constructive phase should also be 4. The stop criterion executed in the second phase must be between 1000 and 100000. The proposed heuristic can be flexibilized enough to solve problems of a varied nature. It could also be applied to other forest optimization problems, such as: allocation of forest yards, forest regulation and routing of vehicles for forest transport.

References

1. Kayo C, Oka H, Hashimoto S, Mizukami M, Takagi S (2015) Socioeconomic development and wood consumption. J For Res 20(3): 309-320.
2. Bostedt G, Mustonen M, Gong P (2016) Increasing forest biomass supply in northern Europe – countrywide estimates and economic perspectives. Scand J For Res 31(3): 314-322.
3. Arce JE, MacDonagh P, Friedl RA (2004) Geração de padrões ótimos de corte através de algoritmos de traçamento aplicados a fustes individuais. Rev Árvore 28(2): 207-217.
4. Arce JE (2000) Um sistema de análise, simulação e otimização do sortimento florestal em função da demanda por multiprodutos e dos custos de transporte.
5. Kohler S, Lrineu Wolff N, Figueiredo Filho A, Arce J (2014) Dynamic of assortment of Pinus taeda L. plantation in different site classes in Southern Brazil. Sci For Sci 42: 403-410.
6. Kohler SV, Koehler HS, Figueiredo Filho A, Arce JE (2015) Machado sda. Evolução do sortimento em povoamentos de pinus taeda nos estados do paraná e santa catarina. Floresta 45(3): 545.
7. Bilici E, Akay A. Evaluating the Performance of Optimal Log Bucking Decision Simulator. In: ; 2018.
8. Tanir D, Ugurlu O, Guler A, Nuriyev U (2016) One-dimensional Cutting Stock Problem with Divisible Items : 12.
9. Garey MR, Johnson DS (1979) Computers and Intractability: A Guide to the Theory of NP-Completeness. New York, NY, USA: WH Freeman & amp Co.
10. Menon MU (2005) Meta-heurísticas na Otimização do Sortimento Florestal.
11. Campos BPF, Binoti DHB, Silva ML da, Leite HG, Binoti MLM da S (2013) Conversão de árvores em multiprodutos da madeira utilizando programação inteira. Rev Árvore 37(5): 881-887.