Multilayer Engine for Microsurgery and Nano Biomedicine Volume 4 - Issue 4

Afonin SM*

• National Research University of Electronic Technology, MIET, Moscow, Russia

Received: February 17, 2020;   Published: February 24, 2020

Corresponding author: Afonin SM, National Research University of Electronic Technology, MIET, Moscow, Russia

DOI: 10.32474/SCSOAJ.2020.04.000193

Abstract PDF

Abstract

In this paper, the structural circuit of the multilayer engine for microsurgery and nano biomedicine is received. We obtained the characteristics of the multilayer engine.

Keywords: Multilayer engine; Structural circuit

Introduction

The multilayer engine with the piezoelectric or electrostriction effects is used for microsurgery and nano biomedicine [1-9]. We received the structural circuit of the multilayer engine in contrast to Cady’s and Mason’s equivalent circuits [9-32]. We determined the mathematical model and the structural circuit of the multilayer engine with the equation of the electro elasticity and the matrix of the quadripole for the multilayer engine.

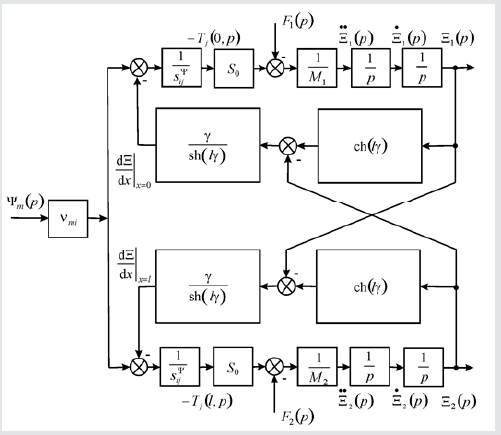
Structural Circuit of the Multilayer Engine

We received the structural circuit of the multilayer engine for microsurgery and nano biomedicine in difference from Cady’s and Mason’s equivalent circuits [1–14]. We have the matrix equation electro elasticity [7,8,14] in the form

S_i = v_mi Ψ_m + s_ij^Ψ T_j

In this equation we write the relative displacement, the coefficient of electro elasticity, the control parameter, the elastic compliance, the mechanical stress in the forms S_i, v_mi, Ψ_m, s_ij^Ψ, T_j

The causes force for the multilayer engine has the form

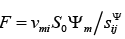
where S₀ is the area of the multilayer engine
The matrix of the quadripole for the multilayer engine [7, 29, 31] has the form

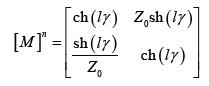
In this equation we write l is the length of the multilayer engine and γ is the coefficient propagation.
We have the structural circuit of the multilayer engine for microsurgsery and nano biomedicine on Figure 1 from its mathematical model in the form

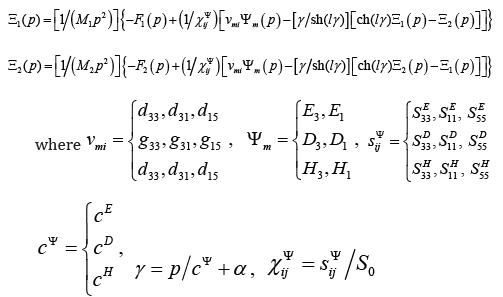
We have the matrix equation of the multilayer engine for microsurgery and nano biomedicine in the form

[Ξ(p)]= [W(p)][P(p)]

In this equation we write the matrixes [Ξ(p)], [W(p)], [P(p)].
In static for the multilayer engine with longitudinal piezo effect and one fixed end we received displacement in the form

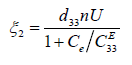
where C_e , C^E₃₃ are the rigidity of the load and the rigidity of the multilayer engine for E = const . We received for the multilayer engine at d₃₃ = 4⋅10⁻¹⁰ m/V, n=12, U=200V, C^E₃₃ = 2⋅10⁷ N/m, C_e = 0.4∙10⁷ N/m the static displacement ξ₂ = 800 nm. We obtained the transfer function with lumped parameters of the multilayer engine with longitudinal piezo effect and one fixed end in the form

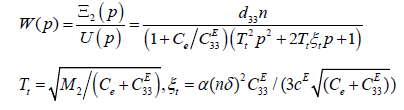
where T_t , ξ_t are the time constant, the damping coefficient of the multilayer engine. Therefore, for the multilayer engine at d₃₃ = 4⋅10⁻¹⁰ m/V, n = 12, U = 200 V, M₂ = 4 kg, 7 C^E₃₃ = 2∙10⁷ N/m, C_e= 0.4∙10⁷ N/m we have ξ₂ = 800 nm and T_t = 0.4∙10^-3 s.

Conclusion

The structural circuit of the multilayer engine for microsurgery and nano biomedicine is obtained. The characteristics of the multilayer engine are received with using its structural circuit.

References

1. Schultz J, Ueda J, Asada H (2017) Cellular Actuators. Butterworth-Heinemann Publisher, Oxford, pp. 382.
2. Afonin SM (2019) Condition absolute stability of control system with electro elastic actuator for nano bioengineering and microsurgery. Surgery and Case Studies Open Access Journal 3(3): 307–309.
3. Zhou S, Yao Z (2014) Design and optimization of a modal-independent linear ultrasonic motor. IEEE transaction on ultrasonics, ferroelectrics, and frequency control 61(3): 535-546.
4. Przybylski J (2015) Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering structures 84: 140–151.
5. Uchino K (1997) Piezoelectric actuator and ultrasonic motors. Boston, MA: Kluwer Academic Publisher pp. 347.
6. Karpelson M, Wei GY, Wood RJ (2012) Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical 176: 78-89.
7. Afonin SM (2015) Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of computer and systems sciences international 54(3): 424-439.
8. Afonin SM (2008) Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady physics 53(3): 137-143.
9. Afonin SM (2006) Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady mathematics 73(2): 307-313.
10. Cady WG (1946) Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London, UK, pp. 806.
11. Mason W (1964) Physical Acoustics: Principles and Methods. Vol.1. Part A. Methods and Devices. Academic Press, New York, USA, pp. 515.
12. Zwillinger D (1989) Handbook of Differential Equations. Academic Press, Boston, pp. 673.
13. Afonin SM (2015) Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and Nanomaterials: Fundamentals, Developments and Applications. Parinov IA (Eds.), Nova Science, New York, USA, pp. 225-242.
14. Afonin SM (2017) A structural-parametric model of electroelastic actuator for nano- and micro displacement of mechatronic system. Chapter 8 in Advances in nanotechnology. Bartul Z, Trenor J (Eds.), Nova Science, New York, USA, 19: 259-284.
15. Afonin SM (2012) Nano- and micro-scale piezo motors. Russian engineering research 32(7-8): 519-522.
16. Afonin SM (2007) Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers,” Mechanics of solids 42(1): 43-49, doi:10.3103/S0025654407010062.
17. Afonin SM (2014) Stability of strain control systems of nano-and micro displacement piezo transducers. Mechanics of solids 49(2): 196-207.
18. Afonin SM (2017) Structural-parametric model electro magnetoelastic actuator nano displacement for mechatronics. International Journal of Physics 5(1): 9-15.
19. Afonin SM (2019) Structural-parametric model multilayer electro magnetoelastic actuator for nanomechatronics. International Journal of Physics 7(2): 50-57.
20. Afonin SM (2016) Solution wave equation and parametric structural schematic diagrams of electro magnetoelastic actuators nano- and micro displacement. International Journal of Mathematical Analysis and Applications 3(4): 31-38.
21. Afonin SM (2018) Structural-parametric model of electro magnetoelastic actuator for nano mechanics. Actuators 7(1): 1-9.
22. Afonin SM (2016) Structural-parametric models and transfer functions of electro magnetoelastic actuators nano- and micro displacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59.
23. Afonin SM (2017) Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and micro displacements under transverse piezoelectric effect. Mechanics of Solids 52(1): 81-94.
24. Afonin SM (2018) Multilayer electro magnetoelastic actuator for robotics systems of nanotechnology, Proceedings of the 2018 IEEE Conference EIConRus pp. 1698-1701.
25. Afonin SM (2018) Electro magnetoelastic nano- and micro actuators for mechatronic systems. Russian Engineering Research 38(12): 938-944.
26. Afonin SM (2018) Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics 5(1):8-12.
27. Afonin SM (2018) Electro magnetoelastic actuator for nano mechanics. Global Journal of Research in Engineering. A: Mechanical and Mechanics Engineering 18(2): 19-23.
28. Afonin SM (2018) Structural–parametric model electro elastic actuator nano– and micro displacement of mechatronics systems for nanotechnology and ecology research. MOJ Ecology and Environmental Sciences 3(5):306‒309.
29. Afonin SM (2010) Static and dynamic characteristics of multilayered electro magnetoelastic transducer of nano- and micrometric movements. Journal of Computer and Systems Sciences International 49(1): 73-85.
30. Afonin SM (2009) Static and dynamic characteristics of a multi-layer electro elastic solid. Mechanics of Solids 44(6): 935-950.
31. Afonin SM (2019) Structural-parametric model and diagram of a multilayer electro magnetoelastic actuator for nano mechanics. Actuators 8(3): 1-14.
32. Bhushan B (2004) Springer Handbook of Nanotechnology. Berlin, New York, USA, pp. 1222.