Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6760
Short Communication(ISSN: 2643-6760) 
Condition Absolute Stability of Control System with Electro Elastic Actuator for Nano Bioengineering and Microsurgery Volume 3 - Issue 3
Afonin SM*
- National Research University of Electronic Technology MIET, Russia
Received: September 23, 2019; Published: September 27, 2019
Corresponding author: Afonin SM, National Research University of Electronic Technology MIET, Moscow, Russia
DOI: 10.32474/SCSOAJ.2019.03.000165
Abstract
In this paper, we used the frequency methods for Lyapunov stable control system to calculate the condition absolute stability of the control system with electro elastic actuator for nano bioengineering and microsurgery. We receive the stationary set of the control system of the hysteresis and butterfly deformation of the electro elastic actuator in form the segment of the straight line.
Keywords: Condition absolute stability; Control system; Electro elastic actuator; Transfer function; Hysteresis and butterfly characteristics; Stationary set; Piezoactuator
Introduction
The condition absolute stability on the derivative for the control system deformation of the electro elastic actuator for nano bioengineering and microsurgery is determined [1,2]. The control systems with electro elastic actuator on piezoelectric, electrostrictive effects solves problems of the matching in the nano bioengineering and microsurgery, the compensation of the temperature and gravitational deformations of the equipment, the correction in the adaptive laser system [1-14]. The electro elastic actuator for nano bioengineering and microsurgery is used in the scanning tunneling microscopy and the gene manipulator [15-31].
Condition Absolute Stability of Control System
The electro elastic actuator on piezoelectric, electrostrictive effects is used in the control systems for the micro and nano surgical repairs, the micro and nano robotics, the micro and nano manipulators and injectors for electro elastic [1-6]. The aim of this work is to calculate the condition of the absolute stability for control system of the deformation of the electro elastic actuator for nano bioengineering and microsurgery. The frequency methods for Lyapunov stable control system are used to determine the condition of the absolute stability of control system [2] with electro elastic actuator. We receive the sufficient absolute stability condition of the Lyapunov stable control system with the hysteresis nonlinearity of the electro elastic actuator using the Yakubovich absolute stability criterion with the condition on the derivative. This criterion is the development of the Popov absolute stability criterion [2]. The description of the hysteresis nonlinearity of the electro elastic actuator [16] in the form
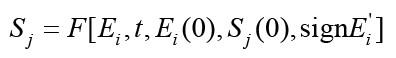
where 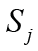 is the relative displacement of the cross section of the
electro elastic actuator along
is the relative displacement of the cross section of the
electro elastic actuator along 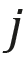 axis,
axis, 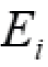 is the control parameter in
the form the electric field strength of the electro elastic actuator
along i axis on the interval [0,t], the initial value of the electric
field strength
is the control parameter in
the form the electric field strength of the electro elastic actuator
along i axis on the interval [0,t], the initial value of the electric
field strength 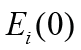 the value of t, the initial value the relative
displacement
the value of t, the initial value the relative
displacement 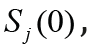 and the sign of the rate
and the sign of the rate 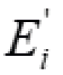 of the electric field
strength variation. Let us consider hysteresis characteristic of the
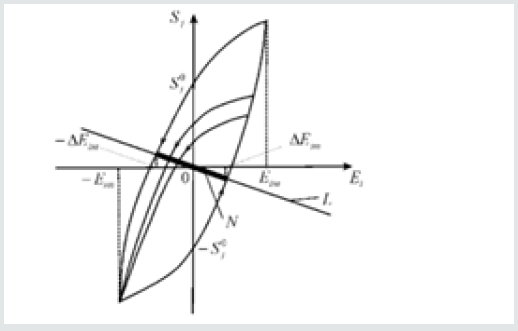
deformation of the electro elastic actuator on (Figure 1). The set
of the electric field
strength variation. Let us consider hysteresis characteristic of the
deformation of the electro elastic actuator on (Figure 1). The set
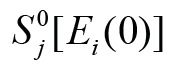 the vertical segment
the vertical segment 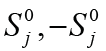 bounded by the points of
intersection of the ordinate axis with the hysteresis loop at the
maximum admissible field strength in the piezoactuator. We receive
for the stable linear part of the control system the stationary set N
and the equation for the straight-line L has the form
bounded by the points of
intersection of the ordinate axis with the hysteresis loop at the
maximum admissible field strength in the piezoactuator. We receive
for the stable linear part of the control system the stationary set N
and the equation for the straight-line L has the form
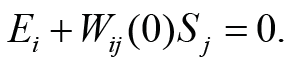
In static regime for the control system for the deformation
of the piezoactuator we receive the value of the transfer function
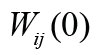 of the linear part of the control system. The set of points N for
intersection of this straight line L with the hysteresis characteristic
represents the segment of the straight line marked. At
of the linear part of the control system. The set of points N for
intersection of this straight line L with the hysteresis characteristic
represents the segment of the straight line marked. At 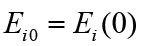 and
and
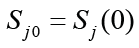 we have the stationary solution to the control system with
hysteresis on Figure 1. We obtain the stationary set in the form of the marked segment N of straight-line L in Figure 1 with the set
of pairs
we have the stationary solution to the control system with
hysteresis on Figure 1. We obtain the stationary set in the form of the marked segment N of straight-line L in Figure 1 with the set
of pairs 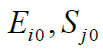 The set of points N for intersection of this straight
line L with the hysteresis characteristic. For the stationary set the
equation has the following form
The set of points N for intersection of this straight
line L with the hysteresis characteristic. For the stationary set the
equation has the following form
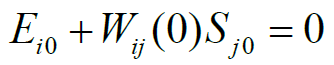
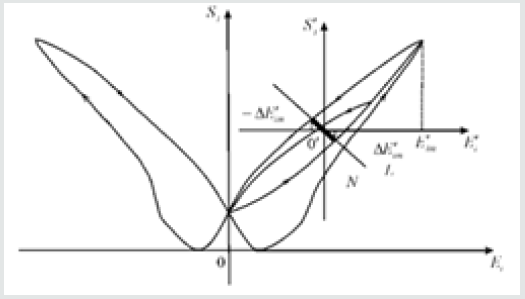
Let us consider butterfly characteristic of the deformation of the
electro elastic actuator for nano bioengineering and microsurgery.
For the actuator with the electrostrictive effect the deformation
characteristic on butterfly wings is observed for unipolar change
of the electric field strength on Figure 2. We have the particular
cycle on one wing of butterfly in the form of the hysteresis loop. For
butterfly type characteristic deformation of actuator in the control
system the coordinate origin is moved to new zero with top dash on
Figure 2. We have stationary set N of the system marked segment
of straight-line L in Figure 2. We receive the continuous function
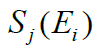 the hysteresis loop of the piezoactuator and the quantities of
the derivative
the hysteresis loop of the piezoactuator and the quantities of
the derivative
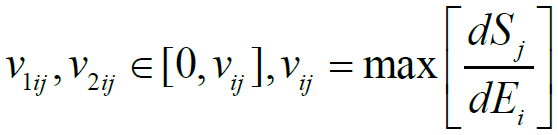
where the quantities of the derivative and are calculated using the hysteresis characteristic on Figure 1 for the maximum admissible electric field strength in the piezoactuator. The quantities and are the minimum and the maximum values of the tangent of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezoactuator. Thus, we obtain
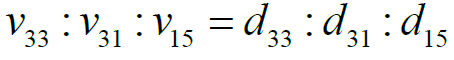
where the ratios of the tangents of the inclination angle of the tangent line to the hysteresis nonlinearity of the piezoactuator for longitudinal, transverse and shift piezoeffects are proportional to the ratios of the piezomodules. We have the expression for the sufficient condition absolute stability of the system with the hysteresis nonlinearity of the electro elastic actuator using the Yakubovich absolute stability criterion with the condition on the derivative. The Yalubovich criterion is the development of the Popov absolute stability criterion [2]. The sufficient condition absolute stability the control system for the deformation of the actuator at ν1ij=0 and ν2ij=νij have the form
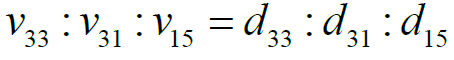
Figure 3: Absolute stability criterion for control system with electro magneto elastic actuator, shaded corrected characteristic.
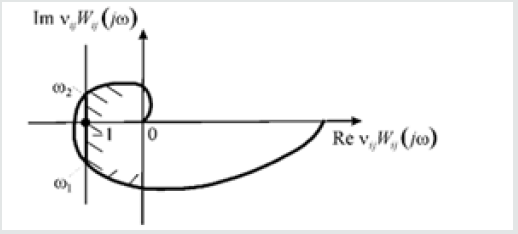
Here 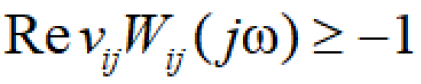 is the amplitude-phase characteristic of the
open-loop system and in brackets j is the imaginary unity and
is the amplitude-phase characteristic of the
open-loop system and in brackets j is the imaginary unity and 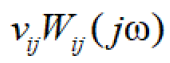 is the frequency The amplitude-phase characteristic of the openloop
system
is the frequency The amplitude-phase characteristic of the openloop
system  on (Figure 3) should be situated to the right
of the straight line
on (Figure 3) should be situated to the right
of the straight line
for all values of 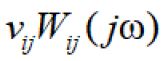
For the piezo actuator from PZT we received the value of the
maximum tangent of the inclination angle of the tangent line to
hysteresis nonlinearity about 1 nm/V for longitudinal piezo effect
and 0.6 nm/V for transverse piezo effect.
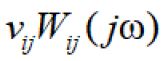
Conclusion
For hysteresis and butterfly characteristic in the control system of the deformation of the electro elastic actuator we obtained the stationary set in the form the segment of the straight line bounded by hysteresis loop. The frequency methods are used for calculating the condition absolute stability of the control system with electro elastic actuator for nano bioengineering and microsurgery. We received condition absolute stability on the derivative for the control system with the electro elastic actuator for nano bioengineering and microsurgery.
References
- Schultz J, Ueda J, Asada H (2017) Cellular actuators. Oxford: Butterworth-Heinemann Publisher. 382 p.
- Yakubovich VA (2002) Popov's method and its subsequent development. European Journal of Control 8(3): 200-208.
- Zhou S, Yao Z (2014) Design and optimization of a modal-independent linear ultrasonic motor. IEEE Transaction on Ultrasonics, Ferroelectrics, and Frequency Control 61(3): 535-546.
- Przybylski J (2015) Static and dynamic analysis of a flextensional transducer with an axial piezoelectric actuation. Engineering Structures 84: 140-151.
- Ueda J, Secord T, Asada HH (2010) Large effective-strain piezoelectric actuators using nested cellular architecture with exponential strain amplification mechanisms. IEEE/ASME Transactions on Mechatronics 15(5): 770-782.
- Karpelson M, Wei GY, Wood RJ (2012) Driving high voltage piezoelectric actuators in microrobotic applications. Sensors and Actuators A: Physical 176: 78-89.
- Afonin SM (2015) Block diagrams of a multilayer piezoelectric motor for nano- and microdisplacements based on the transverse piezoeffect. Journal of Computer and Systems Sciences International 54(3): 424-439.
- Afonin SM (2008) Structural parametric model of a piezoelectric nanodisplacement transduser. Doklady Physics 53(3): 137-143.
- Afonin SM (2006) Solution of the wave equation for the control of an elecromagnetoelastic transduser. Doklady Mathematics 73(2): 307-313.
- Cady WG. (1946) Piezoelectricity: An introduction to the theory and applications of electromechancial phenomena in crystals. McGraw-Hill Book Company, New York, London pp. 806.
- Mason W (1964) Physical acoustics: Principles and methods. 1. Part A. Methods and devices. Academic Press. New York, USA pp. 515.
- Zwillinger D (1989) Handbook of differential equations. Boston: Academic Press. 673 p.
- Afonin SM (2015) Structural-parametric model and transfer functions of electroelastic actuator for nano- and microdisplacement. Chapter 9 in Piezoelectrics and nanomaterials: Fundamentals, developments and applications. Parinov IA (edt.) Nova Science, New York, USA pp. 225-242.
- Afonin SM (2017) A structural-parametric model of electroelastic actuator for nano- and microdisplacement of mechatronic system. Chapter 8 in Advances in nanotechnology. Volume 19. Bartul Z, Trenor J () Nova Science, New York, USA pp. 259-284.
- Afonin SM (2012) Nano- and micro-scale piezomotors. Russian Engineering Research 32(7-8): 519-522.
- Afonin SM (2007) Elastic compliances and mechanical and adjusting characteristics of composite piezoelectric transducers. Mechanics of Solids 42(1): 43-49.
- Afonin SM (2017) Structural-parametric model electromagnetoelastic actuator nanodisplacement for mechatronics. International Journal of Physics 5(1): 9-15.
- Afonin SM (2017) Structural-parametric model of piezoactuator nano- and microdisplacement for nanoscience. AASCIT Journal of Nanoscience 3(3): 12-18.
- Afonin SM (2016) Solution wave equation and parametric structural schematic diagrams of electromagnetoelastic actuators nano- and microdisplacement. International Journal of Mathematical Analysis and Applications 3(4): 31-38.
- Afonin SM (2018) Structural-parametric model of electromagnetoelastic actuator for nanomechanics. Actuators 7(1): 1-9.
- Afonin SM (2016) Structural-parametric models and transfer functions of electromagnetoelastic actuators nano- and microdisplacement for mechatronic systems. International Journal of Theoretical and Applied Mathematics 2(2): 52-59.
- Afonin SM (2017) Parametric block diagrams of a multi-layer piezoelectric transducer of nano- and microdisplacements under transverse piezoelectric effect. Mechanics of Solids 52(1): 81-94.
- Afonin SM (2018) Structural-parametric model of electro elastic actuator for nanotechnology and biotechnology. Journal of Pharmacy and Pharmaceutics 5(1): 8-12.
- Afonin SM (2019) A structural-parametric model of a multilayer electroelastic actuator for mechatronics and nanotechnology. Chapter 7 in Advances in nanotechnology. Volume 22. Bartul Z, Trenor J () Nova Science New York, USA pp. 169-186.
- Afonin SM (2019) Structural-parametric model and diagram of a multilayer electromagnetoelastic actuator for nanomechanics. Actuators 8(3): 1-14.
- Afonin SM (2018) Electromagnetoelastic actuator for nanomechanics. Global Journal of Research in Engineering. A: Mechanical and Mechanics Engineering 18(2): 19-23.
- Afonin SM (2019) Structural-parametric model multilayer electromagnetoelastic actuator nanodisplacement for nanomechatronics. International Journal of Physics 7(2): 50-57.
- Afonin SM (2019) Actuator for nano biomedical research. Biomedical Journal of Scientific and Technical Research 19(3): 14300-14302.
- Afonin SM (2018) Electromagnetoelastic nano- and microactuators for mechatronic systems. Russian Engineering Research 38(12): 938-944.
- Afonin SM (2019) Electro elastic actuator for micro and nano surgical repairs. Open Access Journal of Biomedical Engineering and Biosciences 3(2): 270-272.
- Bhushan B (2004) Springer Handbook of Nanotechnology. Berlin, Springer, New York, USA pp. 1222.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...