
Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6736
Mini Review(ISSN: 2643-6736) 
Survey of Results Regarding the Energetic Balance for Some Motions of Newtonian and Non-Newtonian Fluids Volume 2 - Issue 3
C Fetecau1* and J Zierep2
- 1Section of Mathematics, Academy of Romanian Scientists, Romania
- 2Institut für Strömungslehre, University Karlsruhe, Germany
Received: March 01, 2020; Published: March 06, 2020
Corresponding author: Section of Mathematics, Academy of Romanian Scientists, 050094 Bucharest, Romania
DOI: 10.32474/ARME.2020.02.000139
Abstract
Exact expressions for dissipation, power of the shear stress at the wall, the energy variation and the boundary layer thickness are provided for three unidirectional motions of Newtonian and non-Newtonian fluids over an infinite plate that moves in its plane or applies a shear stress to the fluid.
Keywords: Energetic balance; Kinetic energy; Dissipation; Power of the shear stress at the wall
Introduction
The energetic balance for the Rayleigh-Stokes problem of incompressible Newtonian fluids has been studied by Bühler and Zierep [1]. They showed that the energetic balance for an infinite volume of rectangular cross-section with x∈[0,l], z∈[0,1] and the boundary layer thickness corresponding to a fluid motion over an infinite plate are characterized by the relations
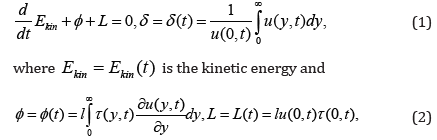
represent the dissipation, respectively the power of the shear
stress at the wall.
Into above relations, the fluid velocity and the non-trivial shear
stress τ ( y,t) given by
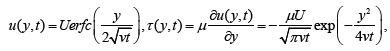 (3)
(3)correspond to the Rayleigh-Stokes problem whose initial and boundary conditions are
u(y,0) = 0 for y > 0;u(0,t)=U fort > 0,and u(y,t)→0as y→∞.(4)
The exact expressions that has been obtained by authors for the four important entities φ , L,δ and / dEkin dt corresponding to the motion in discussion are given by
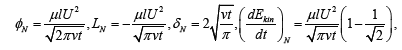 (5)
(5)where μ and υ are the dynamic, respective cinematic viscosities of the fluid. Previous results have been extended to incompressible Oldroyd-B fluids both for the Rayleigh-Stokes problem [2] and the fluid motion due to a constantly accelerating plate [3] or induced by a shear stress on the boundary [4]. In the following we present the obtained expressions for φ , L and δ corresponding to these motions. These expressions can be easy reduced to the similar results corresponding to Newtonian, second grade and Maxwell fluids. The energy variation can be immediately obtained using Equation (1).
Asymptotic Expressions of φ , L and δ For Three Unsteady Motions of Oldroyd-B Fluids
It is well know the fact that the Oldroyd-B fluids contain as special cases both Maxwell and Newtonian fluids. In some motions, like those to be here considered, the governing equations corresponding to Oldroyd-B fluids can be reduced to those of second grade fluids. This is the reason that we present here the general expressions of φ , L and δ corresponding to three unidirectional motions with technical relevance of incompressible Oldroyd-B fluids only.
Rayleigh stokes problem
The initial and boundary conditions corresponding to this
problem are
u(y,0) =∂1u (y,0) = 0 for y >0; u(0,t) = U for t >0 and u(y, t) → as y→∞ (6)
and the three entities φ01, L01 and 01 δ corresponding to this
motion of Oldroyd-B fluids are [2]
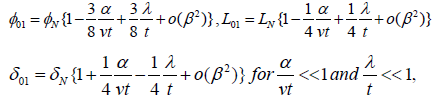 (7)
(7) where β = max{α / (vt),λ / t}.Into above relations λ is the relaxation time corresponding to Maxwell fluids and α = v λr is the first characteristic module of the second grade fluids ( λr being the retardation time corresponding to Oldroyd-B fluids). Taking α = 0 or λ = 0 in Equations (7), the corresponding expressions for second grade, respectively Maxwell fluids are obtained. Making α = 0 in Equations (7), for instance, the known results from [5], Equations (27), (28) and (30) are recovered. If both α and λ are zero the Newtonian results from Equations (5) are obtained.
Motion Due to A Constantly Accelerating Plate
The solutions corresponding to this motion have been obtained
under the conditions
u(y,0) =∂1u (y,0) = 0 for y >0; u(0,t) = At for t >0 and u(y, t) → as y→∞ (8)
and the adequate expressions for the three entities are [3],
Equations (30), (33) and (35)
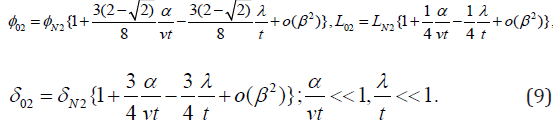
Into above relations the entities corresponding to Newtonian fluids are given by [3, Equation (24)]
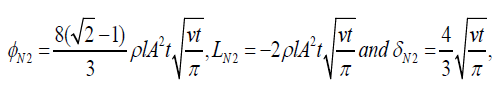 (10)
(10) where ρ = μ / v is the fluid viscosity. Making λ = 0 in Equations (9), for example, we recover the results corresponding to second grade fluids [6], Equations (22) and (23).
Motion Due to A Constant or Time-Dependent Shear Stress on The Boundary
The initial and boundary conditions corresponding to this motion are
u(y,0) =∂1u(y,0) for y >0;(1+λ∂1)τ (y,t) = S at y=0 and u(y, t) → as y→∞ (11)
the adequate expressions of the respective entities are
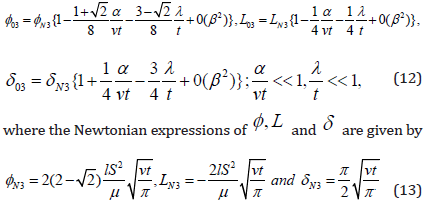
Taking λ = 0 in Equation (11)2, it results that τ (0,t) = S and the adequate expressions for second grade fluids, as well as those for Newtonian fluids given by Equations (13), correspond to a motion induced by a constant shear stress on the boundary. In this case, the values of φ and L are smaller while the boundary layer thickness is greater for second grade fluids as compared to Newtonian fluids. Taking λ = 0 in Equations (12), we recover the results obtained in [7], Equations (37) and (41).
Conclusion
In this short review we provided asymptotic expressions for two characteristic entities of the energy balance and the boundary layer thickness for three motions with engineering applications of Oldroyd-B fluids. In each case, the change of the kinetic energy can be obtained using Equation (1). The exact expressions of these entities, as well as those of the adequate velocity and shear stress fields, are complicated enough to be here included. However, as it results from [2], the profiles of the exact solutions corresponding to velocity and shear stress fields of the Rayleigh-Stokes problem are well enough approximated by those of their asymptotical expressions. It is worth pointing out the fact that the asymptotic expressions that have been obtained for φ , L and δ corresponding to motions of Oldroyd-B fluids can be easy particularized to give the similar results for Newtonian, second grade and Maxwell fluids. Furthermore, a comparison between models can be easy realized. Of special interest is the power of the wall shear stress. This entity describes the energy input that is necessary to keep the medium running and a decisive question is whether it is larger or smaller than in the Newtonian case. Of course, a detailed discussion can be made for each motion but an important remark refers to the boundary layer thickness. It does not depend on the plate velocity or of the shear stress on the boundary and is largest in the case of second grade fluids.
References
- Bühler K, Zierep J (2005) Energetischebetrachtungenzum Rayleigh-Stokes problem. Proc Appl Math Mech 5: 539-540.
- Fetecau C, Hayat T, Zierep J, Sajid M (2011) Energetic balance for the Rayleigh-Stokes problem of an Oldroyd-B fluid.Nonlinear Anal. Real World Appl 12: 1-13.
- Corina Fetecau, Imran MA, Axinte E, Fetecau C (2010) On the energetic balance for the flow of an Oldroyd-B fluid induced by a constantly accelerating plate. Z. Angew. Math Phys 61: 1085-1095.
- Fetecau C, Zierep J, Böhning R, Corina Fetecau (2010) On the energetic balance for the flow of an Oldroyd-B fluid due to a flat plate subjected to a time-dependent shear stress. Comput Math Appl 60: 74-82.
- Zierep J, Fetecau C (2007) Energetic balance for the Rayleigh-Stokes problem of a Maxwell fluid. Int J Eng Sci 45: 617-627.
- Corina Fetecau, Khan M, Asjad MA, Fetecau C (2010) Energetic balance for the flow induced by a constantly accelerating plate in a second-grade fluid. Engineering2: 466-470.
- Vieru D, Siddique I, Kamran M, Fetecau C (2008) Energetic balance for the flow of a second-grade fluid due to a plate subject to a shear stress. ComputMath Appl 56(4): 1128-1137.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...





