Maze Search Using Reinforcement Learning by a Mobile Robot Volume 1 - Issue 2

Makoto Katoh*, Keiichi Tanaka and Shunsuke Shikichi

• Department of Control System Laboratory, Osaka Institute of Technology, Japan

Received: October 03, 2018;   Published: October 10, 2018

*Corresponding author: Makoto Katoh, Department of Control System Laboratory, Osaka Institute of Technology, Japan

DOI: 10.32474/ARME.2018.01.000110

Abstract PDF

---

Abstract

This review presents on research of application of reinforcement learning and new approaches on a course search in mazes with some kinds of multi-point passing as machines. It is based on a selective learning from multi-directive behavior patterns using PS (Profit Sharing) by an agent. The behavior is selected stochastically from 4 kinds of ones using PS with Boltzmann Distribution with a plan to inhibit invalid rules by a reinforcement function of a geometric sequence. Moreover, a variable temperature scheme is adopted in this distribution, where the environmental identification is valued in the first stage of the search and the convergence of learning is shifted to be valuing as time passing. A SUB learning system and a multistage layer system were proposed in this review, and these functions were inspected by some simulations and experiments using a mobile robot.

Keywords: Autonomous; Mobile Robot; Learning; Agent; System Simulation

Introduction

In robots which has begun to spread to not only industrial world but also general home, e.g. cleaning robots etc., recently achievement of complex tasks and adaptation of complex environment has been required and can be done by agents which were concept of distributed artificial intelligent and caught abstractly various robots. Conventionally, as behavior of agents has been controlled by rules designed as if then rules, a lot of rules were required for adaptation to complex environment and achievement of complex tasks. Then, in fact, it is impossible that human designers design an individual rule of each environment.

Then, a lot of reinforcement learning researches, e.g., Q-Learning (QL), Profit Sharing (PS), Instance-Based (IB), which is an unsupervised learning to attain optimal task by learning the environment based on the agent behavior without foresight knowledge on the objects and environments, are paid to attention. The various application areas such as maze search [1], optimal route search [2], a design of dynamic route navigation system using electrical maps [3] have been considered. Especially, a new method of integration with reinforcement learning and A* algorithm which is one of the shortest route search algorithms which do not use learning etc. is groped for in the application to the route search. The advantage of integrating reinforcement learning to such algorithm without learning is that trial and errors of the agent achieves the target even if only the target point is given, and the environment is unknown (Even if the unknown dynamic changes exist).

The reinforcement learning is more effective than the shortest route search algorithms in the case of unknown route as a maze or unknown dynamic change by the way. Then, it is necessary to choose suitable field for them when the field of application of reinforced learning is set. Basic Profit Sharing (PS) has been theoretically considered by Muraoka and Miyazaki [4]. Recently, Kawada proposed the efficient maze search method which improved the action selection machine and the study machine of Profit Sharing (PS). It is an action selection switch type with a premeditated action selection machine, and the method of not strengthening the rule again more than the necessity at learning.

Moreover, it is pointed out that PS is more advantageous than QL in the maze search because the number of steps in PS is convergence which was known from the results of the comparison of numerical value experiment of PS and Q-Learning (QL). Besides, there is a research which is not batch payment but makes the reward installments of two stages in the goal, too.

The purpose of the agent of this research is to learn the action or rule for obtaining the pass towards the goal point after acquiring the key at k point from the start point. Though many studies have linked autonomous agents’ action decisions with maze learning [5], in the maze learning problem by agents, fixed point passing problems which set sub-goals in the middle of a maze are interesting because it can apply the laboratory research to industry.

This review is on the literature [6] of a Japanese conference, which is on the premise that intelligent agents autonomously move mazes, based on selective learning of multidirectional behavior patterns by agents using PS, the problem of searching for a route which the mobile robot moves to the goal points via passing two fixed points by the way was treated as an example of reinforcement learning. Therefore, adopting the time-variant Boltzmann distribution adopted in QL for newly PS, this research emphasis on environmental identification at the initial stage of the search and made a search strategy that focuses on convergence at the latter stage. Also, this review proposes a multistage hierarchical learning system that realizes learning in a complex maze and SUB learning system which realizes learning in a vast maze, so that they aim to speed up learning, instead of paying lump sum payment by goal, focusing on research to be made in two steps of installment payment, characterized by updating the value between sub-goals.

First, this review proposes a SUB learning system to cope with the problem of two-point passing problems in a relatively large maze. The SUB learning system means that the basic algorithm inherits the conventional learning algorithm and learns the course to the fixed point by SUB learning and helps to reach the goal early so that the learning efficiency is raised, and the learning time is shortened. Next, this review proposes a multistage hierarchical system to deal with cases such as when there are duplicate passages in the maze. The multistage hierarchical system ultimately achieves a major goal by dividing measures to achieve small goals into each SUB learning system. This research verifies these functions by simulation and experiment using a mobile robot.

Condition Selection in Course Search

Fixed Point Passing Problem

The 2 fixed point passing problem can be categorized into several types on fixed point passing order, step number, multiple passing method, profit dividing method, searching course dividing method. For example, classification of the fixed-point passing order is as follows.

a) Fixed Order: A → B, B → A, etc., the designer preliminarily determines the order.

b) Any Order: A → B, or B → A, and it is not necessary for the designer to determine the order.

In this research, focusing only on the comparison between the conventional method and the proposed method (SUB learning system and multistage hierarchical learning system) for the convenience of time and space of review, comparative verification shall not be carried out for the effect on the learning performance by the fixed point passing order, the number of steps at the fixed point passing time, the fixed point multiple passing times, the profit distribution method and the search course division method.

Agent Type and Movement Form

There are various kinds of agents, such as wheel type and walking type, 4-way type and 8-direction type, left and right turning type, right / left backward inclined swivel type, etc. can be assumed for the type of agent and movement form, but this research reports only the result of development as an agent of wheel type and 4–way of advance, backward, left-right swing type movement, which is the easiest to handle.

Experimental Devices

Environment for Simulations and Experiments

The main components of the general maze are the passage for the agent to pass, walls, people and other agents. Here, we call the component to heading to a place is an agent, such as a wall or a passage, which is fixed and does not need to heading to a place, is a static omnidirectional object, a person or another agent, etc. moving on its own judgment, which do not need to heading to a place is a dynamic omnidirectional object. On the other hand, there is a need of work for the agent, and an object to be directed toward the direction by the agent is called a directional object. In some cases, it may be static like a fixed point or a goal, or it may be dynamic, such as giving things to people or other agents.

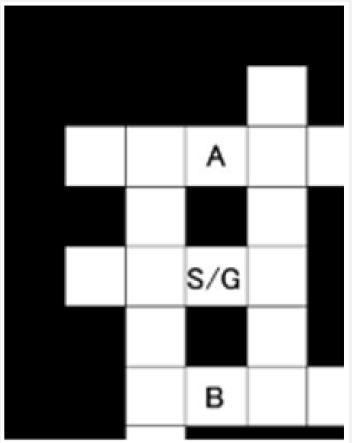
Therefore, in this study, the aisles and walls are static omnidirectional objects, and the fixed points and goals are static oriented objects. As a simulation environment, the maze is shown in Figures 1 & 2. Also, in the example of maze, black squares are walls of static omnidirectional objects. Map A and Map B are both 5×7 squares maze. Here, A and B are the fixed points of the directional object, and in the case where it is not mentioned specifically, the fixing order of A → B, S/G is the start and goal, starting from S/G, passed through each fixed point, reaching S/G is the goal. That is, it is a circulation type maze. Other types of maze include a type that enters from the outside of the maze and goes out of maze, and a type that reaches another inside goal from the internal start.

Khepera

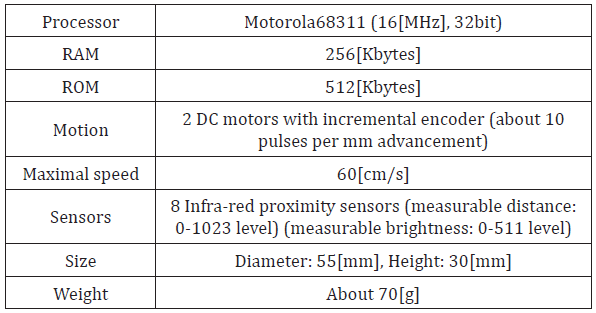
The compact mobile robot Khepera (Figure 3) used for experiments is a wheel-type compact mobile robot system for research and development which had been developed at the Institute of Microcomputer and Interface of the Federal Institute of Technology Lausanne, Switzerland (Table 1).

Results and Discussion

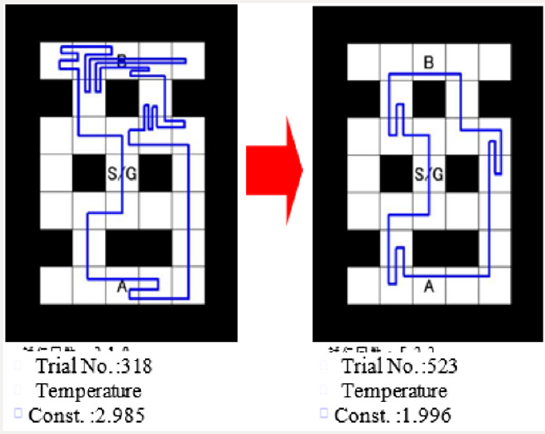
Figure 3 shows the trace display of the simulation results on the Map C differed from Figure 1 for reducing the number of steps, and when the number of trials increases from 300s to 500s, the number of steps required to the goal is almost halved. In the latter half of convergence emphasis, it is found that the temperature constant is reduced from 3 to 2. This approach is expected on the contribution to facilitate course searches of two fixed points passing problems by new combination of SUB learning and multistage hierarchical learning. Moreover, this approach is expected to reduce the number of steps required to the goal as learning progresses and to be useful to search courses in unknown plants or factories by mobile robots (Figure 4) (Appendix 1).

Conclusion

This research pointed out that from the findings of applied research on reinforcement learning, it is effective not only for the unknown environment for agents but also for unknown dynamic changes in the middle of known environments at the beginning as advantages of general shortest path search algorithm. When there is an unknown dynamic change in the middle, it is difficult to match the timing of the change between the simulation environment and the real environment, and a method to effectively set the real environment must wait for future research. However, even when it is unknown in a static environment, if only the result of the route search in the simulation environment is set to the real environment, the influence of the length of the search time on the work in the real environment can be minimized.

Therefore, this review sets up simple problems of cyclic maze with only static obstacles and presented two examples of maze search problem by reinforcement learning using a small mobile robot Kepera which can turn as 90 degree in the same position and find the neighbor walls by the 8 sensors. Finally, the results of simulation are shown by two maps (first half and second half) traced by the mobile robot, that is, the number of steps required to the goal is almost 1/2. In the latter half of convergence emphasis, the temperature constant is reduced to 2/3.

References

1. RS Sutton (1996) Generalization in Reinforcement Learning - Successful Examples using Sparse Coarse Coding. Advances in Neural Information Processing Systems 8: 1038-1044.
2. Y Nakamura, S Ohnishi, K Ohkura, K Ueda (1997) Instance-Based Reinforcement Learning for Robot Path Finding in Continuous Space. Proceedings of IEEE International Conference of System, Man and Cybernetics 1997(2): 1229-1234.
3. Zou Liang, Xu Jianmin, Zhu Lingxiang (2005) Designing Dynamic Path Guidance System Based on Electronic Maps by using Q-learning. Proceedings of SPIE International Society of Optimization Engineering 5985(2): 1005-1009.
4. Hiroki Muraoka, Kazuteru Miyazaki, Hiroaki Kobayashi (2011) Study on Propagation of the Failure Probability in the Reinforcement Learning with Penalty and Reward. Preprints of the 54^th Joint Automatic Conference pp. 1160-1163.
5. Yoshihide Yamashiro, Atsushi Ueno, Hideaki Takeda (2004) Delayed Reward-Based Genetic Algorithms for Partially Observable Markov Decision Problems. Transaction of The Institute of Electronics Information and Communication 35(2): 66-78.
6. K Tanaka, M Katoh (2006) A consideration on two fixed passing problems and moving forms of agents in course searches. Proceedings of JSME Annual Conference G(18-1): 3806.