Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6736
Mini Review(ISSN: 2643-6736) 
Magnus Force in Inertial Microfluidics-Based Devices Volume 2 - Issue 1
Ali Farajpour1, Mergen H Ghayesh1* and Hamed Farokhi2
- 1School of Mechanical Engineering, University of Adelaide, South Australia, 5005, Australia
- 2Department of Mechanical and Construction Engineering, Northumbria University, Newcastle upon Tyne, NE1 8ST, UK
Received:April 09, 2019; Published:April 18, 2019
Corresponding author:Mergen H Ghayesh, School of Mechanical Engineering, Australia
DOI: 10.32474/ARME.2019.02.000127
Abstract
In this paper, the influences of Magnus force on the behaviour of small particles inside a microfluidics- based device are theoretically investigated. The Magnus force is a lift force, which is caused by the rotation of particles within fluid flow. Explicit relations are presented for calculating the Magnus force exerted on small particles inside fluid flow with small Reynolds numbers. Moreover, the effects of the radius of a particle on the Magnus force are discussed. The obtained results and formulation would be helpful in the design of inertial microfluidics-based devices.
Keywords:Inertial Microfluidics; Particle Separation; Magnus Force; Microsystems
Introduction
Microtechnology and nanotechnology [1-8]. have many promising applications in various areas of science and medicine. Particularly, in medicine, novel diagnosis and treatment techniques have been introduced using microscale and nanoscale devices [9]. These techniques are ultra-fast, portable, less costly and easy to use compared to traditional techniques [10]. In addition, in engineering, microscale structures [11-23]. and nanoscale structures [24-31]. have been utilized to fabricate microscale and nanoscale devices such as ultra small actuators, sensors and energy harvesters. Among different microscale systems, inertial microfluidics-based devices have attracted much interest from scientific communities due to their potential for the separation of particles and fluids at ultra-small levels. When a particle travels inside the channel of a microfluidics-based device, it is subject to several forces such as drag, diffusion, Saffman and Magnus forces. In this paper, Magnus force, as one of important forces in a group of microfluidics-based devices, is investigated. A mathematical explicit relation is given for the Magnus force. Furthermore, the effect of particle radius on the Magnus force is studied in detail.
Magnus Force
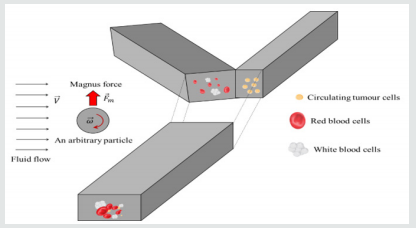
In this section, the Magnus force is formulated, and the influence
of particle radius on this force is studied. Let us consider a spherical
particle within the fluid of constant Velocity 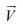 and density
and density 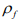 (Figure 1). The fluid is assumed to be incompressible and viscous.
Furthermore, at the beginning, the particle is symmetrically
surrounded by the fluid. The angular velocity and radius of the
particle are denoted by
(Figure 1). The fluid is assumed to be incompressible and viscous.
Furthermore, at the beginning, the particle is symmetrically
surrounded by the fluid. The angular velocity and radius of the
particle are denoted by 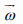 and R, respectively. It is assumed that
there is no relative motion between the particle and fluid on the
interface. When the particle starts to spin as shown in Figure 1, the
fluid velocity below the particle is lower than the one above the
particle. As a result, the pressure is higher below the particle, and
this leads to a lift force. This lift force, which is technically
called Magnus force, is calculated by the following relation for
small Reynolds numbers [32].
and R, respectively. It is assumed that
there is no relative motion between the particle and fluid on the
interface. When the particle starts to spin as shown in Figure 1, the
fluid velocity below the particle is lower than the one above the
particle. As a result, the pressure is higher below the particle, and
this leads to a lift force. This lift force, which is technically
called Magnus force, is calculated by the following relation for
small Reynolds numbers [32].
Figure 1: Magnus Force Exerted on An Arbitrary Particle In A Microfluidics-Based Device For The Separation Of Circulating Tumor Cell.
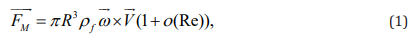
where o(Re) is a function of Reynolds number (i.e. 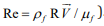 ). The dynamic viscosity of the
). The dynamic viscosity of the
fluid is denoted by 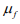 . For particles with a very small radius,
which is the case in microfluidic devices,
. For particles with a very small radius,
which is the case in microfluidic devices,
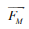 is independent of
is independent of 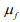 . In microfluidic devices, in addition to
rotation, particles usually travel along
. In microfluidic devices, in addition to
rotation, particles usually travel along
the channel. Let us consider a small particle, which spins with
angular velocity 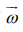 and travels
and travels
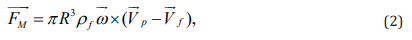
with velocity 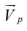 inside the fluid. In this case, the Magnus force
is given by
inside the fluid. In this case, the Magnus force
is given by
in which 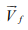 and are
and are 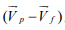 , respectively, the fluid velocity
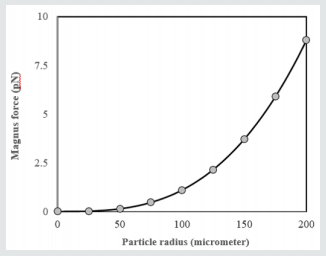
and relative velocity. Figure 2 shows the variation of the Magnus
force with particle radius. The results are calculated for the blood
flow with density 1060 kg/m3
and velocity 0.33 mm/s. It is observed
that the Magnus force rapidly increases with increasing the radius
of the particle. The formula and results of this paper would be
useful in the analysis of fluid-conveying ultra small systems such as
ultra small tubes conveying fluid [33-39] as well as microfluidicsbased devices [40-42].
, respectively, the fluid velocity
and relative velocity. Figure 2 shows the variation of the Magnus
force with particle radius. The results are calculated for the blood
flow with density 1060 kg/m3
and velocity 0.33 mm/s. It is observed
that the Magnus force rapidly increases with increasing the radius
of the particle. The formula and results of this paper would be
useful in the analysis of fluid-conveying ultra small systems such as
ultra small tubes conveying fluid [33-39] as well as microfluidicsbased devices [40-42].
Conclusion
The effect of Magnus force on the motion of particles with relatively small sizes inside an inertial microfluidic device has been examined. Explicit relations were given for determining the Magnus force acting on particles within fluid flow of small Reynolds numbers. It was observed that the Magnus force acts as a lift force and is caused by the rotation of particles. In addition, it was concluded that the radius of the particle has a significant role to play in the Magnus force. The Magnus force substantially increases with increasing particle radius.
References
- Şimşek M (2016) Nonlinear free vibration of a functionally graded nanobeam using nonlocal strain gradient theory and a novel Hamiltonian approach, International Journal of Engineering Science 105: 12-27.
- Farokhi H, Ghayesh MH (2018) Nonlinear mechanics of electrically actuated microplates, International Journal of Engineering Science 123: 197-213.
- Ghayesh MH (2018) Mechanics of tapered AFG shear-deformable microbeams, Microsystem Technologies 24(4): 1743-1754.
- Ghayesh MH (2018) Functionally graded microbeams: Simultaneous presence of imperfection and viscoelasticity. International Journal of Mechanical Sciences 140: 339-350.
- Ghayesh MH, Farokhi H, Amabili M (2013) Nonlinear behaviour of electrically actuated MEMS resonators. International Journal of Engineering Science 71: 137-155.
- Ghayesh MH, Farokhi H, Alici G (2015) Size-dependent electro-elastomechanics of MEMS with initially curved deformable electrodes, International Journal of Mechanical Sciences 103: 247-264.
- Farokhi H, Ghayesh MH (2017) Nonlinear thermo-mechanical behaviour of MEMS resonators, Microsystem Technologies 23(12): 5303-5315.
- Farokhi H, Ghayesh MH (2016) Size-dependent behaviour of electrically actuated microcantilever-based MEMS. International Journal of Mechanics and Materials in Design 12(3): 301-315.
- Shafiee H, Wang S, Inci F, Toy M, Henrich TJ, et al. (2015) Demirci, Emerging technologies for point-of-care management of HIV infection. Annual review of medicine 66: 387-405.
- Warkiani ME, Khoo BL, Wu L, Tay AK, Bhagat AA, et al. (2016) Ultra-fast, label-free isolation of circulating tumor cells from blood using spiral microfluidics. Nature protocols 11(1): 134-148.
- Farokhi H, Ghayesh MH (2017) Nonlinear resonant response of imperfect extensible Timoshenko microbeams. International Journal of Mechanics and Materials in Design 13(1): 43-55.
- Farokhi H, Ghayesh MH, Gholipour A, Hussain S (2017) Motion characteristics of bilayered extensible Timoshenko microbeams. International Journal of Engineering Science 112: 1-17.
- Farokhi H, Ghayesh MH, Hussain S (2016) Dynamic stability in parametric resonance of axially excited Timoshenko microbeams, Meccanica 51: 2459-2472.
- Farokhi H, Ghayesh MH, Kosasih B, Akaber P (2016) On the nonlinear resonant dynamics of Timoshenko microbeams: effects of axial load and geometric imperfection. Meccanica 51(1): 155-169.
- Ghayesh MH (2019) Viscoelastic dynamics of axially FG microbeams. International Journal of Engineering Science 135: 75-85.
- Ghayesh MH (2019) Viscoelastically coupled dynamics of FG Timoshenko microbeams, Microsystem Technologies 25(4): 651-663.
- Ghayesh MH, Farajpour A (2018) Vibrations of shear deformable FG viscoelastic microbeams. Microsystem Technologies 25(4): 1387-1400.
- Ghayesh MH, Farajpour A (2019) A review on the mechanics of functionally graded nanoscale and microscale structures. International Journal of Engineering Science 137: 8-36.
- Ghayesh MH, Farokhi H (2016) Coupled nonlinear dynamics of geometrically imperfect shear deformable extensible microbeams. Journal of Computational and Nonlinear Dynamics 11(4): 041001.
- Farokhi H, Ghayesh MH, Hussain S (2016) Viscoelastically coupled size-dependent dynamics of microbeams. International Journal of Engineering Science 109: 243-255.
- Farokhi H, Ghayesh MH (2017) Nonlinear mechanics of doubly curved shallow microshells. International Journal of Engineering Science 119: 288-304.
- Farokhi H, Ghayesh MH (2018) Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Communications in Nonlinear Science and Numerical Simulation 59: 592-605.
- Rashvand K, Rezazadeh G, Mobki H, Ghayesh MH (2013) On the sizedependent behavior of a capacitive circular micro-plate considering the variable length-scale parameter. International Journal of Mechanical Sciences 77: 333-342.
- Farajpour A, Ghayesh MH, Farokhi H (2018) A review on the mechanics of nanostructures. International Journal of Engineering Science 133: 231-263.
- Ghayesh MH, Farajpour A (2018) Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. International Journal of Engineering Science129: 84-95
- Farajpour A, Rastgoo A, Farajpour M (2017) Nonlinear buckling analysis of magneto-electro-elastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Composite Structures 180: 179-191.
- Farajpour A, Ghayesh MH, Farokhi H (2019) Large-amplitude coupled scale-dependent behaviour of geometrically imperfect NSGT nanotubes. International Journal of Mechanical Sciences 150: 510- 525.
- Farajpour MR, Shahidi A, Farajpour A (2018) Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermo-electromagnetic field: a theoretical study. Micro & Nano Letters 13(11): 1627- 1632.
- Farajpour M, Shahidi A, Farajpour A (2018) A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Materials Research Express.
- Farajpour, Shahidi A, Tabataba’i-Nasab F, Farajpour A (2018) Vibration of initially stressed carbon nanotubes under magneto-thermal environment for nanoparticle delivery via higher-order nonlocal strain gradient theory. The European Physical Journal Plus 133: 219.
- Asemi SR, Farajpour A (2014) Vibration characteristics of doublepiezoelectric-nanoplate-systems. Micro & Nano Letters 9(4): 280-285.
- Rubinow S, Keller JB (1961) The transverse force on a spinning sphere moving in a viscous fluid, Journal of Fluid Mechanics 11: 447-459.
- Ghayesh MH, Farokhi H, Farajpour A (2019) A coupled nonlinear continuum model for bifurcation behaviour of fluid-conveying nanotubes incorporating internal energy loss. Microfluidics and Nanofluidic 23: 34.
- Ghayesh MH, Farokhi H, Farajpour A (2018) Chaotic oscillations of viscoelastic microtubes conveying pulsatile fluid, Microfluidics and Nanofluidics 22: 72.
- Ghayesh MH, Farokhi H, Farajpour A (2019) Global dynamics of fluid conveying nanotubes. International Journal of Engineering Science.
- Farajpour A, Farokhi H, Ghayesh MH (2019) Chaotic motion analysis of fluid-conveying viscoelastic nanotubes. European Journal of Mechanics-A/Solids 74: 281-296.
- Farajpour A, Farokhi H, Ghayesh MH, Hussain S (2018) Nonlinear mechanics of nanotubes conveying fluid. International Journal of Engineering Science 133: 132-143.
- Ghayesh MH, Farokhi H (2018) On the viscoelastic dynamics of fluidconveying microtubes. International Journal of Engineering Science 127: 186-200.
- Ali Farajpour, Mergen H Ghayesh, Hamed Farokhi (2019) Application of nanotubes in conveying nanofluid: a bifurcation analysis with consideration of internal energy loss and geometrical imperfection. Microsystem Technologies.
- Di Carlo D (2009) Inertial microfluidics. Lab on a Chip 9(21): 3038-3046.
- Kuntaegowdanahalli SS, Bhagat AA, Kumar G, Papautsky I (2009) Inertial microfluidics for continuous particle separation in spiral microchannels. Lab on a Chip 9(20): 2973-2980.
- Zhang J, Yan S, Yuan D, Alici G, Nguyen NT, et al. (2016) Fundamentals and applications of inertial microfluidics: A review. Lab on a Chip 16(1): 10-34.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...