Experimental Identification of the Liquor Preheating Process in a Plant Complex Volume 1 - Issue 3

Deynier Montero Góngora*, Ing Gleider Pérez Reyes and Katerin Carcasses Álvarez

• Higher Metallurgical Mining Institute of Moa, Cuba

Received: October 03, 2018;   Published: October 23, 2018

*Corresponding author: Deynier Montero Góngora, Higher Metallurgical Mining Institute of Moa, Center for Energy Studies and Advanced Technology of Moa “CEETAM”, Cuba

DOI: 10.32474/ARME.2018.01.000112

Abstract PDF

---

Abstract

The experimental identification of the liquor preheating process that links the plant complex: Neutral-Leaching-Sulfides, with the scoop of knowing the dynamics of the process for its better study and understanding. It explains the fundamental techniques and methods of identification as well as the input signal to excite the system. The experiments that were carried out are described, the mathematical model obtained is validated and the controller parameters are simulated to optimize the control of the liquor level in the preheating tank.

Keywords: Experimental Identification; Liquor Preheating; Mathematical Model; Controller

Introduction

Automation is of strategic importance in the industrial sector, extractive processes represent a reasonable challenge in this regard. The degree of automation of some industries is often lower than necessary. These aspects cause great losses of energy, raw material and a low quality of the final product, decreasing the competitiveness of companies and increasing the energy consumption that reverts in equipment wear and economic losses. In a historical analysis carried out in Ray [1], it is shown that until the 1960s, practically all the control of chemical processes was done by analogical controllers (mechanical, electrical or pneumatic) designed for the loops of an entrance and an exit. More elaborate control strategies had little acceptance due to the low environmental protection requirements and the fact that the product specifications were less stringent. Improvements in control systems, at that time, would raise costs unacceptably.

With the extensive development that computer resources have had in the last decade, investment in the automation of processes increases significantly, allowing more elaborate control techniques to be implemented. Due to the great diversity of processes and industrial policy issues, these improvements in automation are not widespread in all plants, there are currently metallurgical industries where automation is deficient, particularly in the area of mineral extraction. According to Caldas, Jiménez, Mejía, Hernández, & Avilés [2] to design a control strategy that guarantees the existing demands, a mathematical model must be available that describes the dynamics of the process. This is based on the mathematical process that can be detected through a dynamic or static system; that effectively controls any variable that occurs within any system, using a model that represents its physical structure in communication with the controller of said process.

In this sense, the identification of dynamic systems provides a tool capable of generating methods that allow in a much simpler way, to establish mathematical models with an adequate level of accuracy. In the process of preheating liquor it is important to maintain an adequate control of the level in the storage tank located in the leaching plant. For this, the available liquor capacity of the Neutralization plant and the one demanded by the Sulfuros Plant are also taken into account, guaranteeing a certain liquor flow balance. Faults have been detected in the Liquor preheating process, because the control loop that relates the level of the storage tank with the liquor flow coming from the suction pumps of the Neutralization plant, is working without taking into account a mathematical model that relates the variables of interest of said process (that is, trial and error). In order to solve the problem, the research objective is to obtain a mathematical model of the process, by applying experimental identification techniques that allow proposing the optimal parameters of the system controller.

Materials and Methods

Description of the Technological Scheme of the Product Liquor Preheating Process

To ensure a good leaching, it is necessary to obtain a mixture between pulp and acid, this is achieved by the injection of steam of 650 Lb / in2 through central tubes of agitation and its lower part. Upon reaching the top of the reactor, the steam is separated from the pulp and through the excess steam tube goes to the heater, where it is used for heating. Then the leached pulp flows by gravity, from the “D” reactor to two chillers by train, in the chillers the pulp temperature is reduced to 130 ºC. When passing the same inside the calandria, this yields its heat to the water that surrounds the tubes, producing in this way steam of 15 Lb / in 2 which is used to preheat the pulp to leach and to heat the liquor neutralization product to the sulfide plant. The pulp, once depressurized and deposited in tanks, goes to the distribution box, where it can be diverted to any of the two transfer lines and through them to the laundry section. The steam of 0 Lb / in2 obtained during the depressurization, passes to the separating tanks, in which the pulp particles that may have dragged the steam are eliminated. This steam is used to preheat the liquor product that is sent to a storage tank and from here it is pumped to the sulphide precipitation plant MOP [3].

Current State of Control and Automation of the Process

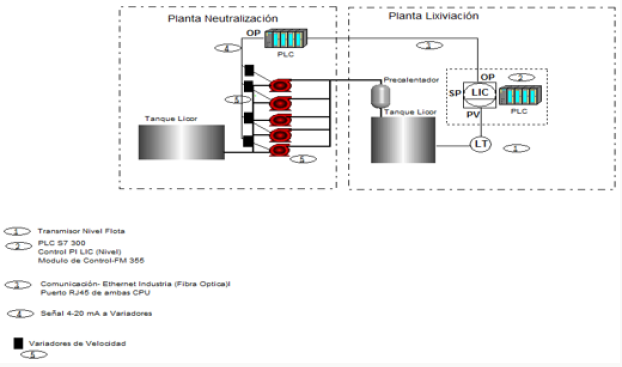
In the plant complex: Neutralization-Leaching-Sulfides, a Supervision and Control System (Citect) is installed, in Figure 1 you can see details of it. There is an S7-300 PLC, which is responsible for receiving all the signals of the different process variables. The measurement of liquor level in the tank is made through a Level Transmitter, which operates a Fleet FIELDVUE DLC3010, by rotating the axis of the torsion tube, this movement of rotation is converted to a current signal that is sent to the Level Indicator Controller. This signal is compared with the reference value of the controller and the flow of liquor is manipulated by means of variable speed drives installed in the motors that operate the suction pumps to maintain the proper level (Figure 1).

Variables Present in the Liquor Preheating Process Inside the Tank

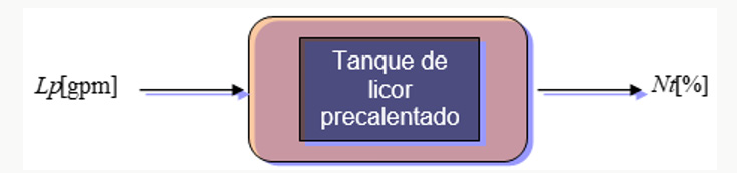
The control problem to be solved is presented in the following way: There is an input variable and an output variable. The manipulated variable considered also input, is the manipulation of liquor flow by speed variators. The variable to control (controlled or output) is the level of the pre-heated liquor tank. These variables can be seen in Figure 2.

Details of the Experimental Identification

It is not difficult to realize that obtaining a mathematical model that describes the process from the phenomenological point of view would be extremely complicated, since the physical-chemical processes involved would lead to differential equations systems in partial derivatives, consequently non-linear and variable over time, we therefore opted for experimental identification to obtain approximate models for different points of operation Nath, Chakrabortiand, & Shekhar [4]. In this case, for the formal mathematical modeling of this process, an experimental identification method was used, consisting of applying as excitation to the system, sequence of positive and negative steps to the flow of liquor entering the tank, in order to identify the process. The mathematical models that were obtained are parametric models. To process the data, the Identification Toolbox of the MATLAB professional package (Ljung [5] was used, which contains tools for obtaining mathematical models of dynamic systems based on the observed input-output data.

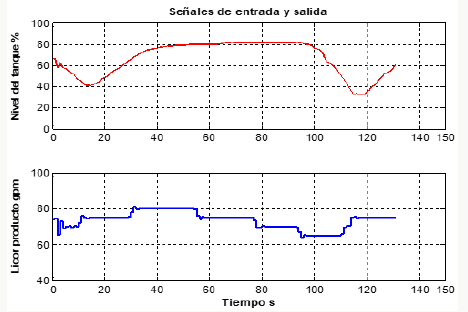
From the analysis of the step responses prior to the system, a time constant of 420s (NT) was estimated. Hence the decision to use a sampling period of the measured signals of 5s. For the identification process, the data was pre-processed. This consisted of suppressing the constant levels and making the average of them be zero. Then the filtering was done following the recommendations of Añez & Scarano [6]. A group of data was selected to estimate the model and another part to validate it. Simple input and simple output models were determined in correspondence by the proposal in Estrada, Peña, & Guarnizo, [7] with Output Error (OE) structures, Box Jenkins (BJ), Auto Regressive with exogenous input (ARX), for different orders . The models were transformed into transfer functions, which are easier to associate with a real plant. The following describes the performance of one of the experiments carried out: 132 data corresponding to the variables (y) were taken. In this case, the speed variators installed in the suction pumps installed in the Neutral plant experienced a variation of 65 to 85% of their total travel. Figure 3 shows the measurements of the input and output variables. For NT, the best model BJ22221 was obtained with an adjustment of 62.75%, which is a model of order 4.

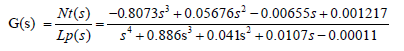
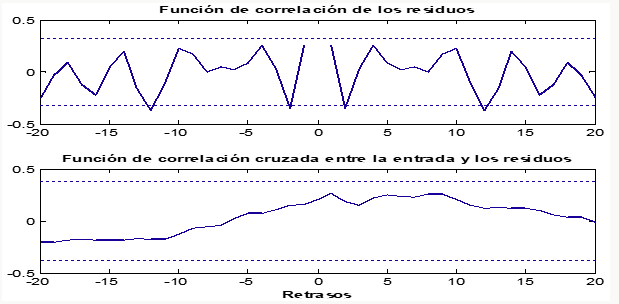
With respect to the validation of the models, residue analysis (prediction errors) was carried out, bearing in mind that certain assumptions were made regarding noise Ljung,[5]. Figure 4 shows that, the function of correlation of the residues is within the levels of confidence and the function of cross-correlation between the waste and the input, reflects its independence, since it does not leave the confidence intervals.

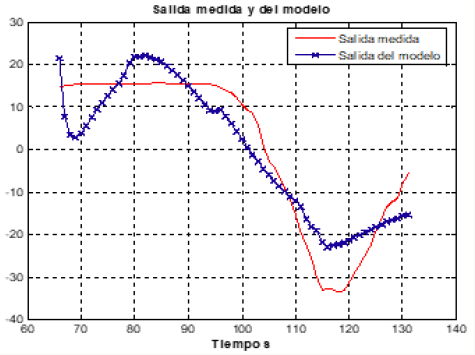
For the validation of the model, the comparison of the output of the model with the real output was made, which is shown in Figure 5, where it is observed that the output of the model is quite close to the real river adjustment.

Driver Adjustment

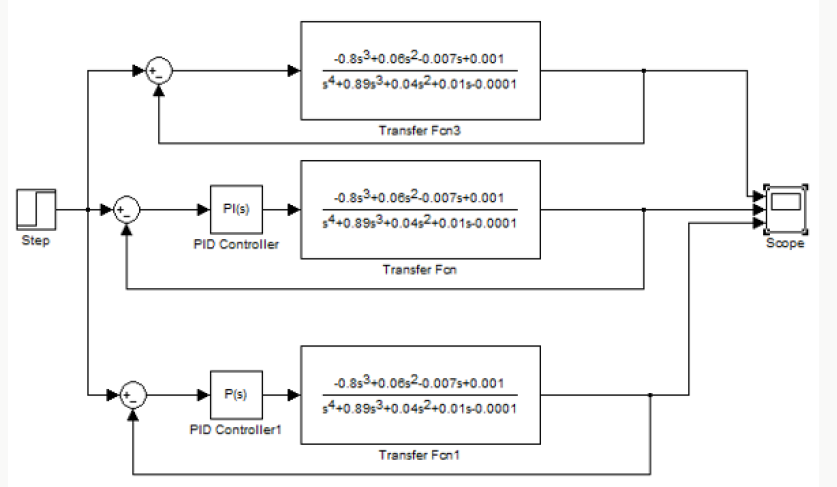
Once the mathematical model was determined, we proceeded to look for the best tuning of the closed loop controllers. For this, the PID Tuner graphic interface invoked by the pidtool command was used from the Command Windows of the MATLAB. For the simulation, a comparison between different configurations of the controllers adapted to the level control loop of the tank (closed loop with the mathematical model of the plant without controller and closed loops with the mathematical model of the plant and controllers type was taken into account). PI and P), which would allow selecting the most optimal configuration (Figure 6).

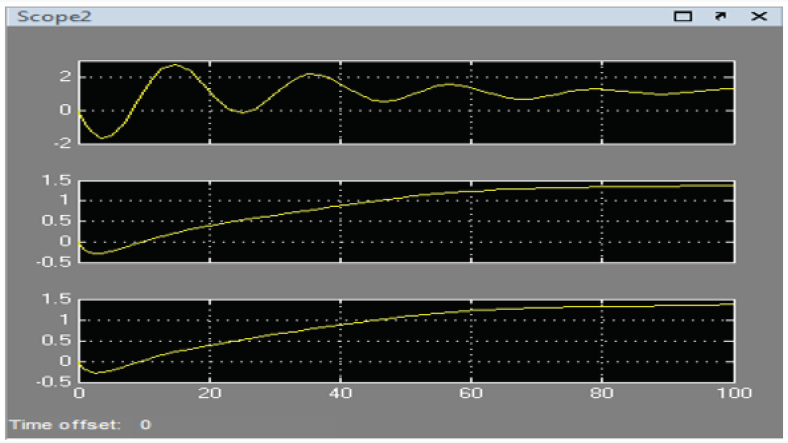
As seen in Figure 7, the behavior of the mathematical model in closed loop is oscillatory and then, for the controller P as for the PI, the stable behavior of the output can be appreciated. In the case of the PID, the output of the system turned out to be unstable. Finally, it is concluded that the best configuration is to use a PI controller with the following parameters: Kc = 0.33145, Ti = 0.0001824.

Conclusion

The liquor preheating process was characterized and the main variables were determined from its analysis as an automatic regulation object.

a) Approximate models were obtained based on the experimental identification that relates the level of the storage tank with the liquor flow manipulated by the speed variators of the motors installed in the suction pumps of the Neutralization plant.

b) The validation of the mathematical models obtained from Box-jenkin 22221 was carried out, which provided 62% adjustments and also an acceptable behavior of the residues was observed.

c) The values of the controller that best simulated the stable behavior of the mathematical models found were proposed.

References

1. Ray WH (1983) Multivariable Process Control-A Survey. Computers & Chem Eng 7(4): 367-394.
2. Caldas O, Jiménez S, Mejía E, Hernández J, Avilés O (2012) Parametric identification in closed loop of pneumatic drive system for double acting cylinder. Faculty of Engineering Magazine. UPTC 21(33): 9-19.
3. MOP (2007) Operations Manual of the “Leaching” Plant of the company.
4. Nath N, Chakrabortiand N, Shekhar R (1998) Reduction of Indian nickeliferrous ore in a fixed bed reactor with gas flowing vertically through the bed. Scandinavian Journal of Metallurgy 27(1): 14-22.
5. Ljung L (2012) System Identification Toolbox. User’s Guide. New Jersey: Prentice-Hall.
6. Añez G, Scarano M (2015) Experimental modeling of the level of a water tank in a pilot plant. Telematique 14(1): 58-78.
7. Estrada I, Peña J, Guarnizo C (2012) Estimation of linear models for the predictive control of small hydroelectric plants. Journal of Postgraduate Solutions EIA (9): 63-78.