
Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6736
Mini Review(ISSN: 2643-6736) 
Buckling Behaviour of Protein Microtubules Volume 2 - Issue 1
Ali Farajpour1, Mergen H Ghayesh1*, Hamed Farokhi2, Alireza Gholipour1 and Harry J Carpenter1
- 1School of Mechanical Engineering, University of Adelaide, Australia
- 2Department of Mechanical and Construction Engineering, North Umbria University, UK
Received: April 26, 2019; Published: May 08, 2019
Corresponding author: Mergen H Ghayesh, School of Mechanical Engineering, University of Adelaide, Australia
DOI: 10.32474/ARME.2019.02.000129
Abstract
Protein microtubules take part in several cellular activities including mitosis, cell movement and migration. During these cellular activities, they can be subject to various types of external loading and pressure. In this study, the bucking of protein microtubules obtained via scale-dependent continuum models are investigated. Several continuum-based formulations, which have been proposed for the buckling of protein microtubules, are reviewed briefly. Finally, the effects of surface elastic properties on the growth rate of buckling in protein microtubules are studied.
Keywords: Protein microtubules; Buckling; Axial loading; Size effects
Introduction
Size effects have a crucial role to play in the statics and dynamics of various ultra-small structures [1-6]. On the other hand, the mechanics of nanostructures [7-14] and microstructures [15-26] is of high importance due to their applications in different nanomechanical and micromechanical systems such as Nano sensors and nanoactuators. Therefore, developing sizedependent mathematical frameworks for analyzing the statics and dynamics of both nanostructures and microstructures would provide a useful tool in nanoengineering and microengineering. Protein microtubules are one of the most important parts of living cells, which participate in many processes inside cells [27,28]. For instance, in the process of mitosis, microtubules help chromosomes to separate and migrate into two opposite positions. In addition, these filaments provide a reliable pathway for protein transportation inside cells. In these processes, microtubules are likely to be subject to various loads such as axial compression. In this study, the buckling instability of protein microtubules under axial compressive loads is investigated. Different size-dependent models of these small-scale structures are also reviewed.
Buckling of Microtubules
Let us consider a single microtubule of length L, inner radius Ri and outer radius Ro. The microtubule has a hollow cylindrical geometry and consists of α and β tubulins, as shown in (Figure 1). It has been proven that size influences have a significant impact on the mechanica0000000l behavior at small-scales [29-36]. Since the inner and outer radii of microtubules are of several nanometers, the nonlocal theory is mostly used to describe size influences. The nonlocal theory is an elasticity-based theoretical tool, which was first utilized by Peddieson et al. [37] for the deformation of nanostructures. According to this theory, we have the following differential equation for the constitutive response of microtubules.
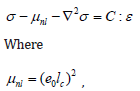
In which σ , C and ε are, respectively, the stress, elasticity and strain tensors; moreover, ∇2 and e0lc stand for the Laplace operator and nonlocal constant, respectively; also, lc and e0 are symbols, which are used for calibrating the model and incorporating the effects of the internal configuration of the structure [38,39]. In addition to nonlocal effects, surface influences have a crucial role to play in the mechanics of ultra small structures such as microtubules. At nanoscales, surface influences become important since the ratio of the surface energy to its bulk counterpart substantially increases. For the microtubule, there are two different surface layers (i.e. outer and inner surface layers). To incorporate surface influences, the following equations can be utilized [40,41].
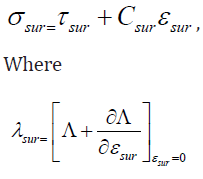
Here “sur” is employed to indicate “surface”. λsur is the residual stress in surface layers [42], and ∧ represents the microtubule surface energy density. Figure 2 depicts the dimensionless growth rate of buckling in protein microtubules [43] subject to axial compression. Calculations are conducted for various surface elastic constants [40]. The horizontal axis of the figure denotes the instability wave number. It is concluded that the growth rate of buckling in microtubules decreases when the elastic constant of surface layers increases. This is because of the fact that the surface elastic constant is associated with an increase in the microtubule stiffness.
Conclusion
The buckling instability of microtubules in human cells has been investigated via scale-dependent theoretical models. Two main scale-dependent theories for the statics and dynamics of microtubules (i.e. surface and nonlocal theories of elasticity) were reviewed briefly. Finally, the influences of buckling wave number and surface elastic constant on the buckling behaviour were studied. It was concluded that higher surface elastic constants substantially reduce the growth rate of buckling in the protein microtubule.
References
- MŞimşek(2016)Nonlinearfreevibrationofafunctionallygradednanobeamusingnonlocalstraingradienttheory and a novel Hamiltonian approach. International Journal of Engineering Science105: 12-27.
- BAkgöz,ÖCivalek (2011)Application of strain gradient elasticity theory for buckling analysis of protein microtubules. Current Applied Physics11(5): 1133-1138.
- HFarokhi, MHGhayesh, Nonlinear mechanics of electrically actuated microplates, International Journal of Engineering Science, 123 (2018)197-213.
- MHGhayesh (2018) Functionallygradedmicrobeams:Simultaneouspresenceofimperfectionandviscoelasticity.International Journal of Mechanical Sciences140: 339-350.
- MHGhayesh, HFarokhi, GAlici (2015)Size-dependent electroelastomechanics of MEMS with initially curved deformable electrodes. International Journal of Mechanical Sciences103: 247-264.
- HFarokhi, MHGhayesh (2016) Sizedependent behaviour of electrically actuated microcantileverbased MEMS. International Journal of Mechanics and Materials in Design12(3): 301-315.
- AFarajpour, MHGhayesh, HFarokhi (2018) A review on the mechanics of nanostructures. International Journal of Engineering Science133:231-263.
- AFarajpour, MHGhayesh, HFarokhi (2019)Largeamplitude coupled scaledependent behaviour of geometrically imperfect NSGT nanotubes. International Journal of Mechanical Sciences150: 510-525.
- MHGhayesh, AFarajpour (2018)Nonlinear mechanics of nanoscale tubes via nonlocal strain gradient theory. International Journal of Engineering Science 129: 84-95.
- AFarajpour, A Rastgoo, MFarajpour (2017) Nonlinear buckling analysis of magnetoelectroelastic CNT-MT hybrid nanoshells based on the nonlocal continuum mechanics. Composite Structures180: 179-191.
- MRFarajpour,AShahidi, AFarajpour (2018) Resonant frequency tuning of nanobeams by piezoelectric nanowires under thermoelectromagnetic field: a theoretical study. Micro & Nano Letters13(11): 1627- 1632.
- SRAsemi,AFarajpour (2014)Vibrationcharacteristicsofdoublepiezoelectricnanoplatesystems,Micro&Nano Letters9(4): 280-285.
- MFarajpour, AShahidi, AFarajpour (2018)A nonlocal continuum model for the biaxial buckling analysis of composite nanoplates with shape memory alloy nanowires. Materials Research Express 5: 035026.
- MFarajpour,AShahidi,FTabatabaiNasab,AFarajpour (2018)Vibrationofinitiallystressedcarbonnanotubes undermagnetothermalenvironmentfornanoparticledeliveryviahigherordernonlocalstraingradienttheory. The European Physical Journal Plus133: 219.
- HFarokhi, MHGhayesh (2017) Nonlinear resonant response of imperfect extensible Timoshenko microbeams. International Journal of Mechanics and Materials in Design13(1):43-55.
- MHGhayesh, HFarokhi (2017) Parametricvibrations of imperfect Timoshenko microbeams. Microsystem Technologies23(10): 4917-4929.
- MHGhayesh (2019)ViscoelasticdynamicsofaxiallyFGmicrobeams: InternationalJournalofEngineeringScience135: 75-85.
- HFarokhi, MHGhayesh, BKosasih, PAkaber (2016) On the nonlinear resonant dynamics of Timoshenko microbeams: effects of axial load and geometric imperfection. Meccanica 51(1):155-169.
- MHGhayesh (2019) Viscoelastically coupled dynamics of FG Timoshenko microbeams. Microsystem Technologies25(2): 651-663.
- HFarokhi, MHGhayesh, SHussain (2016) Dynamic stability in parametric resonance of axially excited Timoshenko microbeams.Meccanica51(10): 2459-2472.
- MHGhayesh, AFarajpour (2019) A review on the mechanics of functionally graded nanoscale and microscale structures International Journal of Engineering Science137:8-36.
- MHGhayesh, AFarajpour (2018) Vibrations of shear deformable FG viscoelastic microbeams. Microsystem Technologies 25(4): 1387-1400.
- HFarokhi, MHGhayesh (2018) Supercritical nonlinear parametric dynamics of Timoshenko microbeams. Communications in Nonlinear Science and Numerical Simulation59: 592-605.
- MHGhayesh, HFarokhi, SHussain (2016) Viscoelastically coupled sizedependent dynamics of microbeams. International Journal of Engineering Science109:243-255.
- MHGhayesh,HFarokhi (2017)Nonlinearmechanicsofdoublycurvedshallowmicroshells. InternationalJournal of Engineering Science 119: 288-304.
- KRashvand,GRezazadeh,HMobki,MHGhayesh (2013)Onthesizedependentbehaviorofacapacitivecircular microplate considering the variable lengthscale parameter. International Journal of Mechanical Sciences77: 333-342.
- KESawin, KLeGuellec, MPhilippe, TJMitchison, (1992) Mitotic spindle organization by a plusenddirected microtubule motor. Nature359(6395): 540-543.
- MAJordan,LWilson (2004)Microtubulesasatargetforanticancerdrugs. NatureReviewsCancer4:253-265.
- AFarajpour,MHGhayesh,HFarokhi (2019)Acouplednonlinearcontinuummodelforbifurcationbehaviourof fluidconveying nanotubes incorporating internal energy loss. Microfluidics and Nanofluidics23:34.
- HFarokhi, MHGhayesh, AGholipour, SHussain (2018) Modal interactions and energy transfers in largeamplitude vibrations of functionally graded microcantilevers. Journal of Vibration and Control24(17):3882-
- AFarajpour, HFarokhi, MHGhayesh (2019) Chaotic motion analysis of fluidconveying viscoelastic nanotubesEuropean Journal of MechanicsA/Solids74: 281-296.
- MHGhayesh,HFarokhi,AFarajpour (2019)Globaldynamicsoffluidconveyingnanotubes. InternationalJournal of Engineering Science 135: 37-57.
- AFarajpour, HFarokhi, MHGhayesh, SHussain (2018) Nonlinear mechanics of nanotubes conveying fluid. International Journal of Engineering Science133: 132-143.
- AFarajpour, MHGhayesh, HFarokhi (2019) Application of nanotubes in conveying nanofluid: a bifurcation analysis with consideration of internal energy loss and geometrical imperfection. Microsystem Technologies PP: 1-15.
- MHGhayesh,HFarokhi (2018)Ontheviscoelasticdynamicsoffluidconveyingmicrotubes. InternationalJournal of Engineering Science127:186-200.
- AFarajpour, ARastgoo (2017) Influence of carbon nanotubes on the buckling of microtubule bundles in viscoelastic cytoplasm using nonlocal strain gradient theory. Results in physics7: 1367-1375.
- JPeddieson,GRBuchanan,RPMcNitt (2003) Application of nonlocal continuum models to nanotechnology. International Journal of Engineering Science41(3-5): 305-312.
- YGao, FMLei (2009) Small scale effects on the mechanical behaviors of protein microtubules based on the nonlocal elasticity theory. Biochemical and Biophysical Research Communications387(3): 467-471.
- JWang, YGao (2016) Nonlocal orthotropic shell model applied on wave propagation in microtubules. Applied Mathematical Modelling40(11-12):5731-5744.
- AFarajpour,ARastgoo,MMohammadi (2014)Surfaceeffectsonthemechanicalcharacteristicsofmicrotubule networks in living cells. Mechanics Research Communications57: 18-26.
- RCCammarata (1994) Surface and interface stress effects in thin films. Progress in surface science46:1-
- BFarshi, AAssadi, AAliniaZiazi (2010) Frequency analysis of nanotubes with consideration of surface effects, Applied Physics Letters96(9):093105.
- TLi (2008) A mechanics model of microtubule buckling in living cells. Journal of biomechanics41(8): 1722-

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...







