A Novel Fuzzy Trajectory Tracking Control Design for Wheeled Mobile Robot Volume 2 - Issue 3

Yung-Hsiang Chen*

• Department of Mechanical Engineering, National Pingtung University of Science and Technology, Taiwan

Received: February 21, 2020;   Published: March 04, 2020

Corresponding author: Yung-Hsiang Chen, Department of Mechanical Engineering, National Pingtung University of Science and Technology, No. 1, Shuefu Road, Neipu, Pingtung 91201, Taiwan

DOI: 10.32474/ARME.2020.02.000138

Abstract PDF

Abstract

A novel fuzzy based control design for the trajectory tracking of wheeled mobile robot (WMR) is presented in this paper. This approach can be applied to generate trajectory tracking control commands on WMR movement. The design objective is to specify one fuzzy control law that can force the WMR to track a predefined trajectory for the nonlinear trajectory tracking control of WMR. In general, it is hard to obtain the closed-form solution from this nonlinear trajectory tracking problem, hence we try to treat this trajectory tracking problem from the so-called fuzzy control design concepts. Finally, one testing scenario: circular reference trajectory tracking is applied to performance verification.

Keywords: Wheeled mobile robot (WMR); Fuzzy control law; Trajectory tracking

Introduction

In the past decades, wheeled mobile robots (WMRs) are widely applied in various industrial and service fields which include transportation, inspection and security etc, and attract a lot of attentions. Hence, it becomes more and more important at accurate manipulations of WMR, especially in the trajectory tracking subject. Many existing studies [1-9] about trajectory tracking problem are discussed, but in general, they are too complicated and not easily implemented. Based on this reason, we try to propose a novel fuzzy control law to treat the trajectory tracking problem of WMR.

Mathematical Model and Design Objective

In this section, the mathematical model and the controlled description of WMR will be presented. According to this regular equation and the geometry relationship with the WMR, a nonlinear tracking error dynamic equation for the controlled WMR can be obtained by following equations. A typical model of the WMR, which contains two driving wheels and a passive selfadjusted supporting wheel, with the same radius express by r and separated by 2R. The vector r exhibits the global coordinate frame {O, X, Y} of real-time location for WMR, which is the coordinate of the point C in the universal coordinate frame, and θ is the orientation of the local frame {C, Xc, Yc}. The distance between points r and C are denoted by d. Base on the above definitions, the generalized coordinate of the WMR can be represented as the equation below.

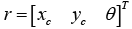(1)

A general WMR system, the robot can move in the direction of the axis of the driving wheels with pure rolling and non-slipping condition status, and the kinematic equation of the WMR under the constraint can be depicted as below [10].

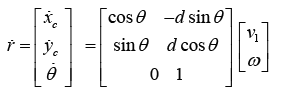(2)

where v₁ and ω are the velocity of linear and angular along the robot axis, respectively.
The above kinematic equation for WMR is used to infer the dynamics of WMR. In this research, the dynamic equation of WMRs can be given as:

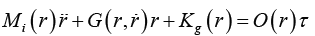(2)

where M(r)∈ℜ^3×3 is a symmetric positive definite inertia matrix and G(r, r)∈ℜ^3×3 is the centripetal and Coriolis matrix.Both M(r) and G(r, r) satisfy the skew-symmetric property and K_g(r) ∈ℜ^3×3 × is the gravitational vector. Since the WMR moves in the horizontal plane, the gravitational vector K_g(r) ∈ℜ^3×3 × is zero, O(r)∈ℜ^3×2 is the input transformation matrix, τ ∈ℜ^2×1 is then applied to the torque vector, r and r, and denotes velocity and acceleration vectors.

We will develop a fuzzy trajectory tracking control design in this paper. The desired trajectory tracking r_r is supposed to exist in limited time functions of the position r_r ∈C² , which is a twice continuously differentiable function. The velocity vector and acceleration vector r_r can be expressed as r_r and r_r , respectively. The definition of the tracking error between the desired trajectory tracking and WMR can be described as the following equation.

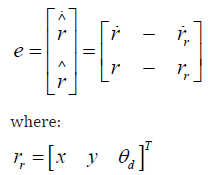(4)

and the tracking error dynamics equation is given as:

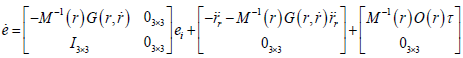(5)

The design objective is to design a fuzzy based control law for the tracking error to approach zero and let the WMR successfully follows the desired trajectory.

Fuzzy Controller Design for Wheeled Mobile Robot Fuzzification

The input and output variables of a fuzzy system are the linguistic variables because they take linguistic values. The input linguistic variables of fuzzy logic-based include: (1). rotation tracking error angle θ , (2). Tracking error in X axis ex and (3). Tracking error in Y axis ey ; besides the output variable is control torque τ . The universe of discourse of the linguistic variable θ is supposed to be [-20, 20] degree, ex is [-2, 2] meter, ey is [-2, 2] meter. About control output, the universe of discourse is set up as [-1, 1] Nm for τ . The linguistic values taken by these variables are expressed by linguistic sets. Each of linguistic variables is assumed to take five linguistic sets as the above and are defined as large negative (LN), large positive (LP), small negative (SN), small positive (SP), and zero (ZE). The linguistic sets are described by their membership functions. To simplify the computation in the actual operation, triangular membership functions are suggested. It has been found that using complex forms of membership functions, such as bell-shaped functions, cannot bring any advantage over the triangular ones.

Defuzzification

The outputs of the linguistic rules are fuzzy, but the control command must be crisp. Therefore, the outputs of linguistic rules must be defuzzified before feeding the WMR plant. The crisp control action is calculated by using the center-of-area (COA) defuzzification procedure.

Simulation Result

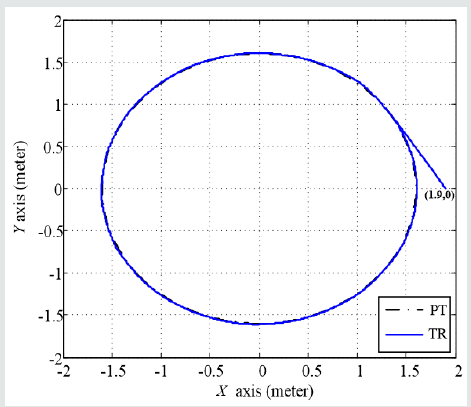
In this section, the proposed fuzzy control law will be verified by tracking a predefined circular reference trajectory as Figure 1. The controlled WMR should precisely follow this predefined trajectory under the force of the proposed method in this scenario. From the simulation result, it is obvious that this proposed method can direct the controlled WMR to track the circular trajectory precisely and quickly.

Conclusion

A novel fuzzy control law is successfully developed for improving the trajectory tracking ability of nonlinear WMR system in this paper. From the simulation result, it is obvious to find out that the proposed fuzzy method achieves a satisfactory performance for tracking the predefined trajectory in circular trajectory.

References

1. Kanayama Y, Kimura Y, Miyazaki F, Noquchi T (1990) A Stable Tracking Control Method for an Autonomous Mobile Robot. in: Proceedings of the IEEE International Conference on Robotics and Automation, USA.
2. Campion G, Bastin G (1996) Structural Properties and Classification of Kinematic and Dynamic Models of Wheeled Mobile Robots. IEEE Transaction Robotics Automation 12(1): 47-62.
3. Ping Z, Nijmeijer H (1997) Tracking Control of Mobile Robots: A Case Study in Backstepping. Automatica33(7): 1393-1399.
4. Oriolo G, Luca A, Vendittelli M (2002) WMR Control via Dynamic Feedback Linearization: Design, Implementation and Experimental Validation.IEEE Transaction Control System Technology 10(6): 835-852.
5. Weiguo W, Hutang C, Yuejuan W (2002) Backstepping Design for Path Tracking of Mobile Robots. in: Proceedings of IEEE/RSJ International Conference on Intelligent Robotics and Systems. Kyongju, South Korea.
6. Tamoghna D, Kar I, Chaudhury S (2006) Simple Neuron-based Adaptive Controller for a Nonholonomic Mobile Robot Including Actuator Dynamics. Neurocomputing 69(16): 2140-2151.
7. Chih C, Tzzuu L,Ying Y (2009) EP-Based Kinematic Control and Adaptive Fuzzy Sliding-Mode Dynamic Contorl for Wheeled Mobile Robots. Information Sciences 179(1): 180-195.
8. Yung C, Tzzuu L, Yue C (2013) A Novel Nonlinear Control Law with Trajectory Tracking Capability for Nonholonomic Mobile Robots: Closed-Form Solution Design. Applied Mathematics and Information Sciences 7(2): 749-754.
9. Yung C, Tzzuu L, Yue C (2013) A Practical Trajectory Tracking Approach for Autonomous Mobile Robots: Nonlinear Adaptive H₂ The Transactions of the Canadian Society for Mechanical Engineering 37(3): 385-394.
10. Yue C, Yung C (2018) Wheeled mobile robot design with robustness properties. Advances in Mechanical Engineering 10(1): 1-11.