Dirichlet Distribution as a Model for Evaluation of the Condition of Adaptive Regulatory Systems in Human Organism in Heart Rate Variability Analysis Volume 4 - Issue 3

Ilyakhinskiy AV¹*, Pakhomov PA¹, Levanov VM² and Mukhina IV²

• ¹Institute of Problems of Machine Science RAS-branch of the Federal State Budget Scientific Institution “Federal Research Center Institute of Applied Physics of the Russian Academy of Sciences,” Russia
• ²Privolzhsky Research Medical University, Russia

Received: October 06, 2020;   Published: October 19, 2020

Corresponding author:Ilyakhinskiy AV, Institute of Problems of Machine Science RAS-branch of the Federal State Budget Scientific Institution “Federal Research Center Institute of Applied Physics of the Russian Academy of Sciences,” Nizhny Novgorod, Russia

DOI: 10.32474/SJPBS.2020.04.000190

Abstract PDF

Introduction

Search for methods of quick human organism condition estimation, early disease and pathology detection including pre-clinical and premorbid stages is still a challenge for the health care service, in particular, in relation to medical and demographic processes including population ageing which is apparent in most developed countries [1]. In preventive medicine in addition to information about disease occurrence and non-occurrence, it is important to be able to qualitatively and quantitatively evaluate the health condition of people from various age, social, occupational groups plus organism’s functional reserves [2]. Nowadays a few methods are known which are based on heart rate variability analysis and indicate the state of regulatory systems of various levels [3,4]. However, each of the said methods has particular limitations which urge researchers to continue searches in the field. The problem articulated at the dawn of the method advent, namely investigation and evaluation human organism’s adaptation processes [5] which might be consistent with aims of physiological studies remains urgent.
The problem is also important in many application aspects, in particular, for prompt control of patients’ state in treatment and rehabilitation processes, and timely diagnostics of disease danger and prevention of related complications. In other words, the information to be acquired may be used for treatment and rehabilitation control, and primary, secondary, and tertiary disease prevention. The purpose of this paper is to examine the capability of the evaluation method for state of adaptive regulatory systems in heart rate variability analysis which is based on the statistical Dirichlet distribution model.

Materials and Study Methods

To evaluate physiological capability of the method we examined a few groups of patients having cerebrovascular pathology and generally healthy people of various ages. We studied: 68 patients (36 female and 32 male) aged 32 to 65 having circulatory system diseases and diagnosed with encephalopathy; 38 patients (20 female and 18 male) aged 32 to 65 having circulatory system diseases and diagnosed with cerebrovascular accident; 38 generally healthy patients (21 female and 17 male) aged 32 to 60 having no cerebrovascular pathology symptoms. The reference group included 23 generally healthy patients under investigation (14 female and 9 male) aged 18 to 23. All people under test were investigated using standard method: electrocardiograms (ECG) were produced for 5 minutes with people at rest in prone position. The electrocardiograms were obtained using Poly-Spectrum-8 electrocardiograph (Neurosoft LLC, City of Ivanovo). The cardiointervalograms were constructed using Poly-Spectrum-Rhythm software and analyzed in a PC using RR Viewer. When developing the method we assumed that regulation system of blood circulation comprises a multi-circuit hierarchically self-organizing system exhibiting non-linearity, sophistication and open nature while dissipative processes including friction, diffusion and dissipation construct ties between components and elements of the said system and generally progressive motion thereof. The complex nature of interaction between elements of the nervous, hormonal, and humoral regulation system and effect on of the state thereof of many external poorly-controlled factors result in that the processes which define heart rate variability exhibit accidental nature and may be represented by a statistical model (statistically) in the form of probability distributions. We proposed to use Dirichlet distribution as the said model. As a model the distribution is informatively equivalent to the object of which state displays the outcome of joint occurrence of n-1 independent processes x_i occurring at rates (intensities) of v_i and opposite in essence to the process occurring at the rate of v_n [6,7]. The function of the Dirichlet distribution which is defined on a k-dimensional simplex is equal to (1).

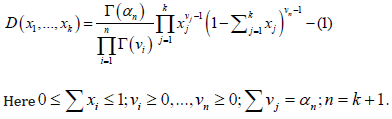
The model agrees with the formal connective between equilibrium thermodynamics and non-equilibrium thermodynamics and is consistent with main provisions of the dissipative structures theory proposed by I. Prigogine, the Nobel Prize winner [8]. Dirichlet distribution entropy can be represented as a sum (2).

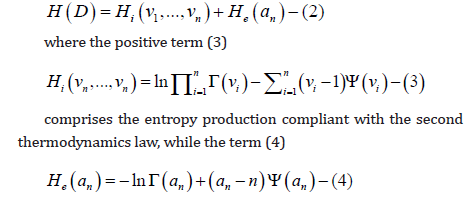
corresponds to the entropic flux accountable for the interaction processes with environment. At n ≥ 3 entropy (4) may be both positive and negative which in Dirichlet distribution model terms makes it possible to regard H_e(a_n) < 0 as one of the selforganization conditions.
The state of homeostasis in control of the autonomic nervous system of cardiac function was assessed [9] by the self-organization indicator value (factor) in control of the autonomic nervous system of cardiac function (Self-organization of Autonomic Nervous System Control - SANSC) expressed by equation (5):

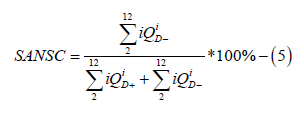
where Dⁱ_{Q −} is the number of Dirichlet models of i-dimensionality with a negative outer entropy value found in temporal series of RR intervals within the investigation period, and Dⁱ_{Q +} is the number of Dirichlet models of i-dimensionality with a positive outer entropy value found in temporal series of RR intervals within the investigation period. Contribution made by individual elements of the autonomic nervous system to the self-organization of vegetative regulation was assessed by the quantity of Dirichlet models found in the temporal series of RR intervals within the investigation period: of 2-4 (parasympathetic nervous system) or 5-7 (sympathetic nervous system) dimensionality with negative outer entropy. Self-organization factor of cardiac function control by the parasympathetic nervous system (Self-organization of Parasympathetic Nervous System Control - SPNSC) as opposed to [9] is calculated from the formula (6).

Self-organization factor of cardiac function control by the sympathetic nervous system (Self-organization of Sympathetic Nervous System Control - SSNSC) is calculated from the formula (7).

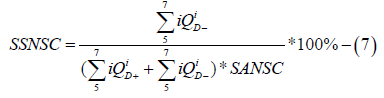
Contribution to cardiac function control self-organization of humoral processes was assessed by the factor value of humoral cardiac function control self-organization (Self-organization of Humoral Control - SHC) (8).

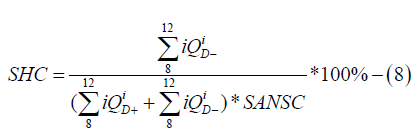
Investigation Results and Discussion

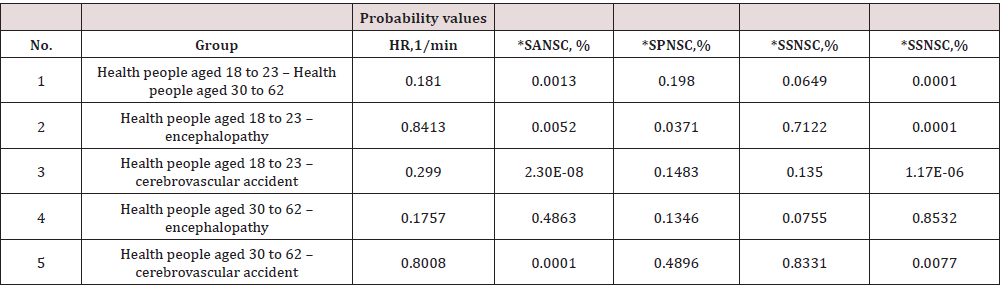
Sample mean values of the state indicators of cardiac function control homeostasis in patients investigated with confidence interval of α=0.01 significance level is tabulated in the Table 1. Probabilities that samples have been taken from general populations with the same average value (independent two-sample t-test) are tabulated in the Table 2. The confidence interval and probability of belonging of the samples to the same general population were assessed using Confidence And T-Test functions in MS Excel. As the Tables show the groups of investigated patients do not differ from each other in heart rate- pulse which indicates inadequacy of traditional clinical methods for severity assessment of patients’ conditions. At the same time there is a significant distinction (α<0.01) between averages of SANSC and SNC self-organization factors for patients in the reference group (healthy people aged 18 to 23) and patients in the groups “healthy people aged 30 to 62” “encephalopathy” and “cerebrovascular accident”. The “healthy people aged 30 to 62” and “encephalopathy” groups differ from the “cerebrovascular accident” group in SANSC indicator with significance value of α<0.01 and SNC indicator with significance value of α<0.1. It is indicative of informative value of statistic heart rate variability indicators (5-8) which significantly describe the organism’s functional condition and may be independent variables if disease severity level.

Significant distinction between “healthy people aged 30 to 62” and “encephalopathy” has not been found in any indicators. The last-mentioned may be explained by undiagnosed preclinical (premorbid) stages of circulatory encephalopathy in a portion of conditionally healthy patients. The results we obtained prove the original concept of reduction of human organism’s adaptive capability when diseases occur. We observe a steady tendency for SANSC adaptation factor to decrease which is governed by disease severity. Besides, contribution of autonomic nervous system elements to the self-organization process drops with disease severity while effect of humoral channel control rises.

Summary

The investigation we carried out has shown that informational and statistical heart rate variability analysis data sufficiently indicate the state of homeostasis of cardiac function control systems both for normal condition and pathology. This fact may be essential in studies of organism functions regulation processes, makes it possible to get the idea about organism’s homeostatic opportunities and numerically evaluate them. The method we propose may be used for treatment and rehabilitation monitoring as well as primary, secondary and tertiary disease prevention.

References

1. Bigger J, Fleiss JL, Steiman RC, Rolnitzky LM, Kleiger RE, et al. (1992) Correlation among time and frequency domain measures of heart period variability two week after acute myocardial infarction. Am J Cardiol 69(9):891-898.
2. State Programme of Health of the Russian Federation.
3. Baevskii RM, Ivanov GG (2007) Heart rate variability: theoretical aspects and possible clinical application. M: Medicine pp: 400-496.
4. (1999) Working team of the European Cardiological Society and North American Stimulation and Electrophysiology Society. Heart rate variability. Standards of measurements, physiological interpretation, and clinical application. Arrhythmology Bulletin 11:53-78.
5. Yabluchansky N (2007) The heart rate variability (HRV) Point: Counterpoint discussion raises a whole range of questions, and our attention has also been attracted by the topic. J Appl Physiol 102:1710-1715.
6. Ilyakhinskiy AV, Sereda Yu S (1989) Statistical models in probing missions. Higher Schools Bulletin, Radiophysics 32(12):1502-1505.
7. Sereda Yu S (1998) Problems of informational and statistical theory. M: Cosmos inform.
8. Prigogine I (1960) Introduction to thermodynamics of irreversible processes. M: Foreign Literature Publishers.
9. Ilyakhinskiy AV, Pakhomov PA, Mukhina IV, Anufriev MA (2017) Informational and statistical measures of the self-organization of the heart regulation systems in the analysis of heart rate variability. Human Physiology 43(3):339-344.