Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2641-1709
Review Article(ISSN: 2641-1709) 
An Actual Statistical Problem with Model Selection My Solution Volume 3 - Issue 1
Kurt Neumann*
- Independent researcher in Szolgagygörpuszta, Hungary
Received:August 08, 2019; Published: August 23, 2019
Corresponding author: Kurt Neumann, Independent researcher in Szolgagygörpuszta, Kerékteleki, Hungary and Principal of EIS Kft, Budapest, Hungary
DOI: 10.32474/SJO.2019.03.000153
Introduction
This manuscript is a follow-up of my last one in SJO where I promised to show you my solution of a client problem. This case has been transformed such, that the logic of the problem remained unchanged and the confidentiality of my client’s data is warranted, however. In the last manuscript the results of the commonly found methods of modelling were shown and discussed. Now we will show my results and a discussion of them. Mathematically speaking the mainstream models already shown could be summarized as two univariate approximations by straight lines or a two-dimensional fit of a plane, describing the dependent variable by an approximation based simultaneously by a constant and two linear terms. I was fully aware of the limitations of the very small sample size of the mainstream models and I hope to successfully use this example to convince my readers about the economic benefits of discussions with professional mathematicians/statisticians instead of users of statistical software as I have classified them.
Methods
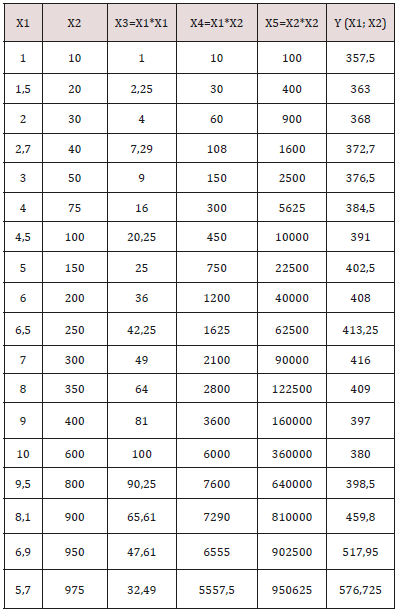
As I was blinded to the actual meaning of the variables X1, X2 and Y my experience indicated that I should try a second order polynomial fit as this would be the simplest possible model extension as compared to the mainstream linear models. The similarity to the considerations of Occam’s razor (see Wikipedia) are also well based on my personal professional experience. My model equation used is displayed below:
Y (X1; X2) =a0 + a1. X1 + a2. X2 + a3. X12 + a4. X1. X2 + a5 .X22 + error term (equ 1)
The above equation contains prior regression analysis the coefficients a0, a1 and a2 for the linear terms and a3, a4 and a5 for second order polynomial terms which must be estimated from the data by means of linear regression based on the method of least squares. The error term must fulfil the assumption that the data points represent statistically independent observations with constant variance in the domain of data points and an approximate Gaussian distribution. The most important data requirement is a continuous and metric measurement scale of the data and based on my long- term experience in medicine and other statistical applications, if fulfilled, the basis for a highly robust behavior of the regression analyses based on least squares. Finally, enough data points must be available. This is a problem in the determination of the sample size, which, in my opinion, requires professional statistical assessment.
Result
The numerical details are shown in Table 1 below with additional information necessary in the Excel data analysis software as the input for Excel’s regression routine:
a) Note 1: X1 and X2 and Y refer to the client provided original data. The author intended to look at a standard polynomial of degree 2 and the calculated data columns indicate all second order terms necessary from Excel logic for that purpose. The contents after the provided Y in the brackets are a help to understand that Y (as provided from my client) is the dependent variable of X1 and X2 in this very model. For physicians unfamiliar with exponential floating-point formatted numbers reading of the Excel online documentation is recommended.
b) Note 2: There are three lines in Table 2. The descriptions in column one show regression in the first, residual in the second and total in the third line. The total in line 3 displays the SS of all data against the grand mean. The residual in line 2 shows the sum of squares of the differences between data and calculated Y values using the coefficients a0, a1, …, a5 and the line 1 described as regression provides us with the information of the explained variation by the calculated regression coefficients. In view of the raw Y data shown in Table 1 we observed therefore a residual variance - in the magnitude of 9,0403. 10-28 which – for practical purposes – might be judged as zero. The mathematical interpretation in everyday language is there is an interpolation problem or a perfect fit between the raw Y data and the regression equation with the calculated coefficients shown in
Table 2: ANOVA analysis of variance table
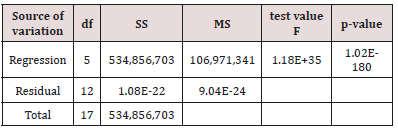
df: degrees of freedom
SS: sum of squares
MS: mean squares (represent the variances which are the squared
standard deviations).
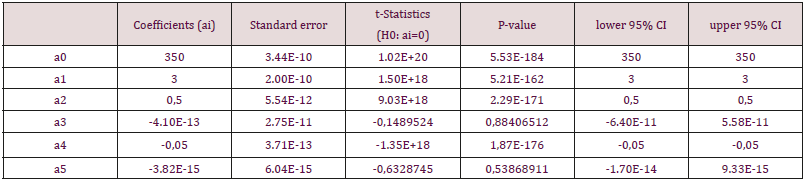
c) Note 3: The coefficients ai refer to the equation (1). Please note that i = 0, 1, 2, …, 5 in column one and a0 is frequently assigned the name intercept. We follow the frequently engaged standard statistical practice of setting not statistically significant coefficients to zero and have the solution of our model (from equation (1)) in equation (2) below:
Y (X1; X2) = 350 + 3. X1 + 0,5. X2 - 0,05. X1. X2 (equ 2)
The inevitable rounding errors which are present in all common computers are reflected in the Excel documentation which states that about ten to twelve digits in decimal results should be reliably exact. Therefore, it seems not to be a problem that 95% confidence intervals cover zero and actual numbers of digits of the raw data in Table 3 justify this decision. We analyzed in addition the model of equation 2 and for practical purposes we concluded that there were perfectly consistent results (data on file but not shown here). You might consider this fact as a simple way to be on the safe side with our conclusions about this data set. Our verbal comment to equation (2) is that the available data set very strongly indicates that a perfect functional relationship between X1, X2 and Y exists. In view of the relatively small sample size of the evaluated data here, it is strongly recommended to collect substantially larger data sets in the next future and only if results could be reproduced within the sampling error limits then an application for the Nobel Price could be envisaged in case our data originated from medical data.
Conclusion/Discussion
The reader should consider several aspects of our example: First, finding practical interpolation from data sets could have apart from chances for a successful Nobel price application and small sample sizes other causes, e. g. that the Y-data is already a derived data item calculated from X1 and X2 actually. The originator of the data set could be consulted, and this issue might sometimes be clarified quickly. Second, a review of the selection criteria might shed additional aspects and one of the most likely finding might be that the data were collected from young, healthy volunteering soldiers instead of a larger sample with males and females in about 1:1 relation. Many other explanations for such a result might be presented here, but I think that an experienced statistician would likely be a valuable contributor to such – admittedly very rare – events. I think under all circumstances the plan for a follow-up study could be quite a challenge for the responsible physician as well. I’d like to emphasize that from a mathematical viewpoint a real and strong and simple functional relationship (interpolation) is likely to be considered as a very strong scientific revelation, finally. Another important consideration was in the results’ section mentioned and I’d like to address it here: In case of a polynomial of degree k with a sample n=k+1 there will be always an interpolation solution, which is just due to lack of sample size and as such not informative at all. My personal experience indicates very strongly that in cases where n-k coefficients are estimated and two k is at least contained in n-k several times then degenerate interpolation could safely be excluded, however.
In my early professional work life I was once confronted to a study to assess the effect of a substance on the blood pressure and heart rate which did not contain blood pressure as a selection criterion. It seemed to everybody as highly representative for the selected patients. Based on some 150 patients the baseline data showed certain, quite considerably big percentages of hypotonic, normotonic and hypertonic patients. The evaluation of baseline to end of treatment differences showed only a very weak linear trend for the changes of systolic, diastolic blood pressure and heart rate. A second order polynomial showed a clear, statistically highly significant quadratic trend: The hypotonic patients showed increased blood pressure data, normotonic had just data varying around zero and hypertonic patients showed statistically highly significant blood pressure reductions. Sponsor’s headquarter asked me to provide the average blood pressures from the full sample and as I assume - the international medical director - decided not to pursue this substance as the pooled average across hypotensive, normotensive and hypertensive patients was medically relatively small compared to the established hypertensive drugs of this pharmaceutical giant. It is no surprise at all, that a subgroup evaluation of the three blood pressure subgroups clearly indicated that young and middle-aged patients revealed quite small shares of hypertensive patients and patients aged over 60 years had considerable shares of hypertensive patients consistent with published literature of epidemiology. Today, I still judge this as a mistake based on the omnipresent linear thinking of the very company’s headquarter. Finally, I think the examples discussed here are at least some evidence that non-linearity can be present in medical data and the consequences could cause major detrimental damages to financial operations of corporations and by withholding potentially interesting drugs from patients’ unnecessary burden of disease(s).

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...