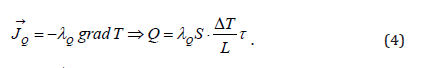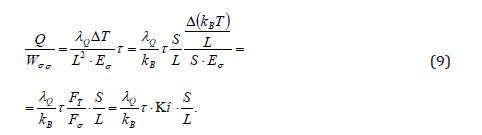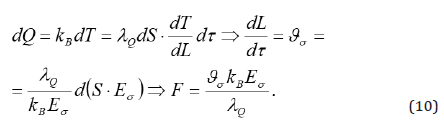Cauchy Modeling as a New Trend in Research of Fullerene- Type Nanomaterials Volume 3 - Issue 1

Petro Kosobutskyy*

• CAD Department, Lviv Polytechnic National University, Ukraine

Received:November 11, 2020;   Published:December 03, 2020

Corresponding author: Petro Kosobutskyy, CAD Department, Lviv Polytechnic National University, Ukraine

DOI: 10.32474/TOOAJ.2020.03.000156

 

Abstract PDF

Abstract

In the work, based on the analysis of heat and gas with acoustic phonons by fullerene, the physical criterion Cauchy is the kind of thermal strength before spring strain, which is caused by the nanotube fullerene

Keywords: Thermal Conductivity; Fullerene; Optimization; Numbers Similarity Numbers

Introduction

Studies of the thermal conductivity of structured nano systems draw attention to the fact that in micro- and nanoelectronics the urgent task of heat dissipation released during the operation of electrical elements [1-6]. So, in the process of electrical switching of the element energy is consumed 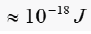which is on the verge of thermal fluctuations This means that a billion (109) transistor chip uses order energy in a single act 10^-3J. Then, in order of speed 1GHz , the energy consumed can reach values 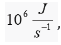far exceeding the power of a jogging electric kettle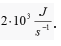

In order to remove Joule-Lenz heat in electric nanoelements, both microchannels with liquid carriers of heat and conductive elements, such as nanocomposite ceramics filled with carbon nanotubes, can be used, which, depending on their chiral characteristics, can alter the physical properties of nano cells. Thus, it was established [9-12] and confirmed by theoretical estimates [13,14] that the thermal conductivity at room temperature of a carbon nanotube can reach values of 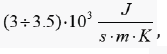which significantly exceeds the thermal conductivity of diamon 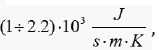which was considered one of the best heat conductors. Carbon nanotubes are thermally stable, characterized by high electrical conductivity [10], high electron mobility [11], and a large specific surface value [15]. It is believed [16] that the abnormally high thermal conductivity of carbon nanotubes is due to their regular structure and the small number of defects and impurity centers in them. In the elementary cell of graphene there are two carbon atoms, so the dispersion spectrum consists of three optical and three acoustic branches, among which the longitudinal and transverse acoustic modes correspond to the speed of sound 2130 and 1360 M/s

If in metals heat is transferred mainly by electrons, then in phononel dielectrics, as quanta of elastic vibrations of a crystal lattice. The speed of the phonons dw(q)/d is determined by the slope of the dispersion curve w(q) so acoustic phonons are faster than optical ones, and therefore acoustic phonons are the main heat carriers. In [8], the Debye model was supplemented by the idea of quantization of elastic waves, which allowed the problem to be reduced to the problem of phonon gas kinetics modeling. The patterns of phonon thermal energy transport [16] have subsequently led to the creation of nanocomposites, in which, unlike crystalline substances, there is in fact no perfect structure and precise geometry [17]. Therefore, if the composite matrix is filled with graphene, its low-frequency phonons interact with the phonons of the matrix, leading to an increase in the thermal conductivity of the heterogeneous system as a whole [18]. In nanoceramic fillers with fullerenetype structures, the main mechanism of thermal energy transfer is related to acoustic phonons. Acoustic phonons are excited and propagated along carbon nanotubes, so the patterns of heat energy transport will depend on the geometric parameters of carbon nanotubes. Although the main contribution to thermal conductivity is the polymer matrix, it can be adjusted by filling with a metal system with high thermal conductivity, and the use of tubular type carbon nanotubes allows to realize the effect of heat transfer due to the ballistic mechanism of thermal conductivity of phonons, when the losses from acoustic losses. The basic model (Landauer – Datta – Lundstrom transport model or LDL model) of heat energy transfer by phonons, as well as electrons, was developed in work [19]. The authors developed the concept of bottom-up modeling of heat transfer effects in electronic devices as nanoscopic ballistic effect devices. The ballistic mechanism works best in short carbon nanotubes with a length less than the average free path length of the acoustic phonons. Based on the analysis of the results (reference [1-3] in work [20], the author of the work [14] believes that fullerenes, along with high mechanical characteristics, have an increased ability to transfer heat energy to the surface layer itself. The regularity of the transfer of heat energy by solids of small size determines the ratio l_m/L often called the Knudsen number (phonon gas is often compared to classical gas). Here l_m is the length of free path of a phonon in a macroscopic body, whose dimensions are much greater [21]. In nanostructures, parameter L is characteristic dimension, so if 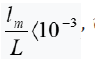then, the diffusion mechanism of heat energy transfer is trueю. If the ratio 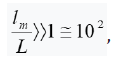known as the so-called Casimir limit, then the magnitude effects become more relevant and the probability of phonon collisions with each other when the phonons propagate from one boundary to the next becomes smaller, that is, in other words, the effect of ballistic heat transfer is enhanced. Therefore, even with an ideal crystalline structure, nanosystems are characterized by a distinct thermal anisotropy of thermal conductivity [22]. In this work, based on a comparative analysis of the thermal conductivity of a carbon nanotube by excitation of acoustic phonons in it, the analysts of the known Cauchy criterion (number) are grounded.

Discussion

In nano systems, transport is determined by the effective electron free path. When the size of the nanoobject becomes smaller than this parameter and becomes commensurate with the de Broglie wave (0.01-0.1 nm), the dependence on the geometric dimensions and shape grows [21]:

where ∞ ∞ l Q λ , are these are the parameters of a macroscopic body, for example graphite. Then use of similarity criteria makes it possible to carry out preliminary qualitative-theoretical analysis and to make a choice of a system of dimensionless parameters, which are determinable in complex physical processes and allows to properly organize the setting of the experiment and to carry out preliminary processing of results [25]. From the point of view of analysis of models of heat transfer with the participation of acoustic vibrations of atoms and molecules in the medium, the criteria of thermal and mechanical processes attract attention:

Fourier number

where m m Ñ ρ is thermal energy per unit volume of a substance. The physical content of the Fourier criterion is that it determines the ratio of heat flux due to thermal conductivity to local heat flux. In other words, the Fourier criterion is equal to the change in the internal energy in the elementary volume, that is, it describes the relation between the stored energy and that propagated in the medium by the coefficient of thermal conductivity Q λ . Resizing of L the system causes a slight acceleration of the thermal energy transfer process for a constant Fourier number over a characteristic time τ . Thus, criterion (2) relates the rate of heat propagation to the thermophysical parameters and the size of the carrier (carbon nanotubes in the case of nanoceramics).

Since the inverse value −1 Q λ characterizes thermal inertia, the electromechanical devices of micron-sized thermal effects are also characterized by low thermal inertia. In addition, as follows from (2), the characteristic transition time decreases by the quadratic law from the characteristic geometric parameter (size) of the active element. Therefore, the thermal actuators in the micro- and nanoscale dimensions are characterized by a rather high speed, virtually inertial, such as thermocouples in the form of micro- or nanoscale beams.

Bio number or thermal similarity criterion

The number Bio describes the relationship between the temperature gradient between the points at a distance L and the so-called temperature head ΔÒ. In other words, the number Bio describes the ratio of thermal resistance −1 Q λ (similar to the electrical resistance −1 R σ of a section of an electrical circuit with electrical conductivity R σ and ohmic resistance R ) to the thermal resistance of a surface through which heat is dissipated into the environment. The Bio criterion belongs to the group of determining criteria because it includes the coefficient of thermal conductivity of a solid medium. Recall that, in contrast to the Bio criterion, the Nusselt criterion, which includes the coefficient of thermal conductivity of a liquid, refers to the determining criteria.

Cauchy number as a criterion for the ratio of the inertia force to the force of elasticity:

This criterion characterizes the regularity that the oscillation frequency is inversely proportional to the length, so the natural oscillations of micro- and nano-oscillators are high-frequency, which limits the operating range of electromechanical devices to natural frequencies and causes high dynamic characteristics. Criterion (3) shows that in the case of elastic deformation, the oscillation frequency is inversely proportional to the geometric dimensions of the oscillator. Therefore, micro and nano electromechanical oscillators have a relatively high frequency of resonant oscillations. This allows them not only to significantly improve their dynamic characteristics with a short reaction time, but also to make them insensitive to external acoustic noise. Other similarity criteria are also known [23].
It is known that the thermal conductivity of a status solid is described by the known Fourier equation:

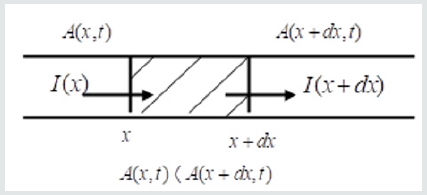
Руку → JQ is the vector of the heat flux density and Q λ is coefficient of thermal conductivity. By definition, the coefficient of thermal conductivity determines the heat flux → JQ in the direction of the space in which there is a temperature gradient, and the minus sign indicates that energy is transferred from the more heated part of the body to the less heated, i.e in the direction of decreasing temperature. Therefore, the temperature gradient grad T is a vector quantity directed along the normal to the isothermal surface in the direction of increasing temperature and numerically equal to a partial derivative of the temperature along this direction. Equation (4) is a first order differential equation with respect to t , does not allow for a substitution of time t on the time − t , which is proof of the irreversibility of the processes it describes. The right part of it expresses the flux density vector in the form of a scalar gradient. This is a vector, so the flow of a scalar value is also a vector, whereas the flow is already a vector of the tensor. It is the Fourier law that introduces the concept of the coefficient of thermal conductivity. The one-dimensional model of process (4) is shown in Figure 1. As follows from (1) and (2), in the case of nanosystems, these criteria depend on the parameter being affected by the dimensional effect. In the crystal lattice, heat carriers are phonons, as quanta of thermal lattice vibrations. Therefore, in the absence of phonon interaction processes, the heat flux in a crystal is similar to heat transfer by convection in a gas flowing through a cylinder open at the ends. Therefore, the known formula can be applied to the energy of the particle system by concentration n of the phonons:

In the case of a carbon nanotube, the elastic vibrations of the lattice occur only in the walls of the tube, so the cross-sectional area is the cross-sectional area S of the layer from which the cylinder collapses. It is here that the temperature gradient between the ends of the tube generates phonon gas with energy equivalent to the energy of elastic deformation of the nanowire

For carbon nanotubes with a wall 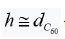thickness and radius R , and the Young’s Young modulus σ E of tensile deformation under the action of tensile strength L F at relative elongation ε is calculated by the formula [26]

According to [27, 28], the characteristic heat transfer time by acoustic phonons in nanostructures is estimated by the formula

where ω_Smax, is equal to the maximum frequency of acoustic phonons. Then for the relation of energies (4) and (6) taking into account (5) we obtain the formula:

An analog of the Cauchy criterion 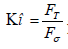introduced here in the form of the ratio of thermal force 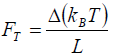to elastic force σ σ F = S ⋅ E . In formula (9) records a one-dimensional internal energy gradient propagating in the form of classical elastic waves in a flat layer with a cross-sectional area S and a length L that is folded into a tube. Then, through the elementary volume of the nanotube wall, the length and cross-sectional area of the nanotube are transmitted over an elementary period of time dτ .

The ratio Q λ 1 characterizes the so-called thermal resistance, and a similar resistance σ E 1 to the propagation of perturbation in the form of elastic deformation. Therefore, it follows from (10) that force resistance to the propagation of local perturbation

is proportional to the velocity that is characteristic of Newton’s resistance to physics.

Conclusion

In the work, based on the analysis of heat and gas with acoustic phonons by fullerene, the physical criterion Cauchy is the kind of thermal strength before spring strain, which is caused by the nanotube fullerene.

Future Directions and Conclusion

The cellular mechanisms involved in glaucoma are yet to be fully elucidated. Understanding these processes will lead to new methods of preventing chronic glaucomatous vision loss when conventional IOP-lowering treatments either fail to prevent progression (up to 20% of glaucoma patients continue to progress to blindness) or adequate target pressures cannot be achieved due to ineffectiveness or poor tolerance to medication. Thus, there is a clear unmet need to target the underlying mechanisms governing the progressive fibrotic remodelling of the LC, to halt the progressive and ongoing fibrotic damage to the LC/ONH and visual field loss. It is clear that there are multiple systemic cellular processes at play simultaneously, and when combined, result in the development of glaucoma. Glaucoma may be described as a multifactorial disease entity, and it is likely that in the future, there will be no ‘one size fits all’ therapeutic option. It is evident, however, that mitochondrial dysfunction plays an integral role in the aetiology of glaucoma, and that the dysregulation of this organelle directly results in RGC susceptibility and vulnerability. Several studies have highlighted promising therapeutic targets in halting or even reversing this progression, including nicotinamide, insulin and metformin. AMPK is a highly conserved master regulator of metabolism, both at the cellular and organismal levels, whose function is extremely relevant not only for normal physiology, but also for the understanding of many metabolic diseases [54]. The examination of novel mechanisms of AMPK as the key metabolic sensor in LC cells in glaucoma will be vital to understand the driving force underlying fibrotic changes occurring in the LC. These activated LC myofibroblasts drive the fibrotic processes occurring in the LC. The glaucoma LC cells adapt to their pro-fibrotic role by increasing their proliferation, reducing apoptosis, and augmenting their metabolism. These activated LC myofibroblasts essentially undergo ‘metabolic reprogramming’ to utilise alternative high-energy sources to enhance cellular growth and development. Halting the pro-fibrotic activity and metabolism of glaucoma LC cells by restoring AMPK expression and activity to normal levels, could lead to a new therapeutic approach to reduce fibrosis in glaucoma. In conclusion, glaucoma is a multifactorial, progressive, chronic optic neuropathy. The second leading cause of irreversible blindness worldwide, the development of novel therapeutics to combat this disease is of paramount importance. This review has identified several key metabolic sensors whose dysregulation and dysfunction directly drive and promote disease development and progression. Whilst there have been several potential treatment options investigated for this disease in the last decade, it is clear that further research and clinical trials to fully determine the suitability and effectiveness of therapeutic targets are necessary.

Conflict of Interest

There is no economic interest or conflict of interest

References

1. Quigley H, Broman AT (2006) The number of people with glaucoma worldwide in 2010 and 2020. Br J Ophthalmol 90(3): 262-267.
2. Crawley L, Zamir SM, Cordeiro MF, Guo L (2012) Clinical Options for the Reduction of Elevated Intraocular Pressure. Ophthalmol Eye Dis 4: 43-64.
3. McDonnell F, O Brien C, Wallace D (2014) The role of epigenetics in the fibrotic processes associated with glaucoma. J Ophthalmol 2014(7): 750459.
4. Wallace DM, Murphy Ullrich JE, Downs JC, O Brien CJ (2014) The role of matricellular proteins in glaucoma. Matrix Biol 37: 174-182.
5. McElnea EM (2011) Oxidative stress, mitochondrial dysfunction, and calcium overload in human lamina cribrosa cells from glaucoma donors. Mol Vis 17: 1182-1191.
6. Yang H (2011) Posterior (outward) migration of the lamina cribrosa and early cupping in monkey experimental glaucoma. Investig. Ophthalmol Vis Sci 52(10): 7109-7121.
7. Tezel G, Trinkaus K, Wax MB (2004) Alterations in the morphology of lamina cribrosa pores in glaucomatous eyes. Br J Ophthalmol 88(2): 251-256.
8. White E, Mantovani A (2014) Spectrum of Tissue Injury and Resolution. J Pathol 229(2): 141-144.
9. Diegelmann RF, Melissa C, Evans (2014) Wound Healing: An Overview of Acute, Fibrotic and Delayed Healing. Front Biosci 9: 283-289.
10. Betensley A, Sharif R, Karamichos DA (2016) Systematic Review of the Role of Dysfunctional Wound Healing in the Pathogenesis and Treatment of Idiopathic Pulmonary Fibrosis. J Clin Med 6(1): 2.
11. Kirwan RP, Wordinger RJ, Clark AF, O Brien CJ (2009) Differential global and extra-cellular matrix focused gene expression patterns between normal and glaucomatous human lamina cribrosa cells. Mol Vis 15: 76-88.
12. Kirwan RP, Felice L, Clark AF, O Brien CJ, Leonard MO (2012) Hypoxia regulated gene transcription in human optic nerve lamina cribrosa cells in culture. Invest Ophthalmol Vis Sci 53(4): 2243-2255.
13. Kirwan RP, Leonard MO, Murphy M, Clark AF, OBrien CJ (2005) Transforming Growth factor-β-regulated gene transcription and protein expression in human GFAP-negative lamina cribrosa cells. Glia 52(4): 309-324.
14. Papageorgis P (2015) TGF β signaling in tumor initiation, epithelial-to-mesenchymal transition, and metastasis. J Oncol 2015: 587183.
15. Liu B (2018) Increased substrate stiffness elicits a myofibroblastic phenotype in human lamina cribrosa cells. Investig. Ophthalmol Vis Sci 59(2): 803-814.
16. Zode GS (2011) Transforming growth factor-β2 increases extracellular matrix proteins in optic nerve head cells via activation of the smad signaling pathway. Mol Vis 17: 1745-1758.
17. Kolliopoulos C (2019) Transforming growth factor (TGF) induces NUAK kinase expression to fine-tune its signaling output. J Biol Chem 294(11): 4119-4136.
18. Schmitt, Segert (2008) 基因的改变 NIH Public Access. Bone 23: 1-7.
19. Inman DM, Harun Or Rashid M (2017) Metabolic vulnerability in the neurodegenerative disease glaucoma. Front Neurosci 11: 1-19.
20. He Y, Ge J, Tombran Tink J (2008) Mitochondrial defects and dysfunction in calcium regulation in glaucomatous trabecular meshwork cells. Investig Ophthalmol Vis Sci 49(11): 4912-4922.
21. Lascaratos G (2015) Resistance to the most common optic neuropathy is associated with systemic mitochondrial efficiency. Neurobiol Dis 82: 78-85.
22. Coughlin L, Morrison RS, Horner PJ, Inman DM (2015) Mitochondrial morphology differences and mitophagy deficit in murine glaucomatous optic nerve. Investig Ophthalmol Vis Sci 56(3): 1437-1446.
23. Ju W (2009) NIH Public Access. 49: 4903-4911.
24. Williams PA, Harder JM, John S WM (2017) Glaucoma as a Metabolic Optic Neuropathy: Making the Case for Nicotinamide Treatment in Glaucoma. J Glaucoma 26(12): 1161-1168.
25. Kamel K, Farrell M, O Brien C (2017) Mitochondrial dysfunction in ocular disease: Focus on glaucoma. Mitochondrion 35: 44-53.
26. Harun Or Rashid M (2020) MCT2 overexpression rescues metabolic vulnerability and protects retinal ganglion cells in two models of glaucoma. Neurobiol Dis 141: 104944.
27. Lee S (2012) Impaired complex-I-Linked respiration and ATP synthesis in primary open-angle glaucoma patient lymphoblasts. Investig Ophthalmol Vis Sci 53(4): 2431-2437.
28. Mimaki M, Wang X, McKenzie M, Thorburn DR, Ryan MT (2012) Understanding mitochondrial complex I assembly in health and disease. Biochim Biophys Acta Bioenerg 1817(6): 851-862.
29. Van Bergen NJ (2015) Measurement of systemic mitochondrial function in advanced Primary Open-Angle Glaucoma and leber hereditary optic neuropathy. PLoS One 10(10): 1-18.
30. Khawaja AP (2016) Assessing the association of mitochondrial genetic variation with primary open-angle glaucoma using gene-set analyses. Investig Ophthalmol Vis Sci 57(11): 5046-5052.
31. Kamel K (2020) Reduced Oxidative Phosphorylation and Increased Glycolysis in Human Glaucoma Lamina Cribrosa Cells. Invest Ophthalmol Vis Sci 61(13): 4.
32. Shirlaw JT (1931) The metabolism of tumours. Br Med J 1: 74.
33. Pavlides S (2012) Warburg meets autophagy: Cancer-Associated fibroblasts accelerate tumor growth and metastasis via oxidative stress, mitophagy, and aerobic glycolysis. Antioxidants Redox Signal 16(11): 1264-1284.
34. Mitchell SJ (2019) HHS Public Access mice. 27: 667-676.
35. Hui F (2020) Improvement in inner retinal function in glaucoma with nicotinamide (vitamin B3) supplementation: A crossover randomized clinical trial. Clin Exp Ophthalmol 48(7): 903-914.
36. Katsyuba E, Auwerx J (2017) Modulating NAD ⁺ metabolism, from bench to bedside. EMBO J 36(18): 2670-2683.
37. Aman Y, Qiu Y, Tao J, Fang EF (2018) Therapeutic potential of boosting NAD⁺ in aging and age-related diseases. Transl Med Aging 2: 30-37.
38. Cantó C (2012) The NAD+ precursor nicotinamide riboside enhances oxidative metabolism and protects against high-fat diet-induced obesity. Cell Metab 15(6): 838-847.
39. Gilley J, Coleman MP (2010) Endogenous Nmnat2 Is an Essential Survival Factor for Maintenance of Healthy Axons. PLoS Biol 8(1): e1000300.
40. Hwang ES, Song SB (2020) Possible adverse effects of high-dose nicotinamide: Mechanisms and safety assessment. Biomolecules 10(5): 1-21.
41. Harrison IF, Powell NM, Dexter DT (2019) The histone deacetylase inhibitor nicotinamide exacerbates neurodegeneration in the lactacystin rat model of Parkinson’s disease. J Neurochem 148(1): 136-156.
42. Fukushima T (2005) Niacin metabolism and Parkinson’s disease. Environ. Health Prev Med 10(1): 3-8.
43. Ulanovskaya AO, Zuhl MA, Cravatt FB (2016) NNMT promotes epigenetic remodeling in cancer by creating a methylation sink. 97: 5421-5433.
44. Akintunde A (2017) Physiological Phenotyping for Personalized Therapy of Uncontrolled Hypertension in Africa. Am J Hypertens 30(9): 923-930.
45. Hemati T, Moghadami Tabrizi N, Davari Tanha F, Salmanian B, Javadian P (2011) High plasma homocysteine and insulin resistance in patients with polycystic ovarian syndrome. Iran J Reprod Med 9(3): 223-228.
46. Liu M (2017) Serum N1-methylnicotinamide is associated with coronary artery disease in Chinese patients. J Am Heart Assoc 6(2).
47. Kannt A (2018) A small molecule inhibitor of Nicotinamide N-methyltransferase for the treatment of metabolic disorders. Sci Rep 8(1): 3660.
48. Emerman AB, Zhang ZR, Chakrabarti O, Hegde RS (2010) Trehalose Is a Key Determinant of the Quiescent Metabolic State That Fuels Cell Cycle Progression upon Return to Growth. Mol Biol Cell 21: 4325-4337.
49. Lin SC, Hardie DG (2018) AMPK: Sensing Glucose as well as Cellular Energy Status. Cell Metab 27(2): 299-313.
50. Chatterjee A, Villarreal G, Oh DJ, Kang MH, Rhee DJ (2014) AMP-activated protein kinase regulates intraocular pressure, extracellular matrix, and cytoskeleton in trabecular meshwork. Investig. Ophthalmol Vis Sci 55(5): 3127-3139.
51. Harun Or Rashid M, Inman DM (2018) Reduced AMPK activation and increased HCAR activation drive anti-inflammatory response and neuroprotection in glaucoma. J Neuroinflammation 15(1): 1-15.
52. Zhang CS (2014) The lysosomal v-ATPase-ragulator complex is a common activator for AMPK and mTORC1, acting as a switch between catabolism and anabolism. Cell Metab 20(3): 526-540.
53. Claus SP (2019) The Strange Case of Prevotella copri: Dr. Jekyll or Mr. Hyde? Cell Host Microbe 26(5): 577-578.
54. Bambang A, Tanadi C, Sumarpo A (2019) Deciphering the role of AMPK-related kinase 5 in human cancer progression and metastasis. Biomed Res Ther 6(10): 3396-3404.
55. Huang X, Lv W, Zhang JH, Lu DL (2014) MiR-96 functions as a tumor suppressor gene by targeting NUAK1 in pancreatic cancer. Int J Mol Med 34(6): 1599-1605.
56. Chen D (2017) Knockdown of ARK5 Expression Suppresses Invasion and Metastasis of Gastric Cancer. Cell Physiol Biochem 42(3): 1025-1036.
57. Suzuki A (2005) Involvement of transforming growth factor-β1 signaling in hypoxia-induced tolerance to glucose starvation. J Biol Chem 280(36): 31567-31563.
58. Zhang HY, Li JH, Li G, Wang SR (2015) Activation of ARK5/miR-1181/HOXA10 axis promotes epithelial-mesenchymal transition in ovarian cancer. Oncol Rep 34(3): 1193-1202.
59. Bell RE (2014) Transcription factor/microRNA axis blocks melanoma invasion program by miR-211 targeting NUAK1. J Invest Dermatol 134(2): 441-451.
60. Brennan EP (2012) Next-generation sequencing identifies TGF-β1-associated gene expression profiles in renal epithelial cells reiterated in human diabetic nephropathy. Biochim Biophys Acta Mol Basis Dis 1822(2): 589-599.
61. Belforte N, Cueva Vargas JL, Di Polo A (2018) AB015 Metabolic stress in glaucoma engages early activation of the energy biosensor adenosine monophosphate-activated protein kinase leading to neuronal dysfunction. Ann Eye Sci 3: AB015-AB015.
62. Reuben J Shaw (2009) LKB1 and AMPK control of mTOR signalling and growth Reuben. Acta Physiol (Oxf) 196(1): 65-80 (2009).
63. Cork GK, Thompson J, Slawson C (2018) Real talk: The inter-play between the mTOR, AMPK, and hexosamine biosynthetic pathways in cell signaling. Front Endocrinol (Lausanne) 9: 1-9.
64. Gwinn DM (2008) AMPK Phosphorylation of Raptor Mediates a Metabolic Checkpoint. Mol Cell 30(2): 214-226.
65. Ogretmen B (2019) 乳鼠心肌提取 HHS Public Access. Physiol Behav 176: 139-148.
66. Li X (2020) Eye Drops of Metformin Prevents Fibrosis After Glaucoma Filtration Surgery in Rats via Activating AMPK/Nrf2 Signaling Pathway. Front Pharmacol 11: 1-14.
67. Bone NB (2018) Metformin reverses established lung fibrosis in a bleomycin model. Na Med 24(8): 1627-1627.