Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2641-6921
Mini Review(ISSN: 2641-6921) 
Investigation Peculiarities of Liquids Solidification Volume 2 - Issue 1
Kozak L*
- Ivano−Frankivsk National Technical Oil and Gas University, Ukraine
Received: September 20, 2019; Published: September 24, 2019
*Corresponding author: Department of Thermodynamics, Ivano−Frankivsk National Technical Oil and Gas University, Ukraine
DOI: 10.32474/MAMS.2019.02.000127
Mini Review
Today there are a large number of studies of solidification processes. They give a general picture of the process based on equilibrium, quasi-equilibrium and kinetic models which describe a mechanism of nucleation and growth of bulk crystals and layers, taking into account thermodynamic, quantum mechanical and molecular statistical analysis of elementary acts. Different models of crystallization complement each other and differ in the consideration of various processes: the movement of the phase boundary, the distribution of crystals by size on the surface and filling the crystal lattice nodes, etc. [1-4]. But at present, a satisfactory theory of the formation of crystals has not yet been created. This is the result, first of all, of great complexities that real crystals hide. If from a thermodynamic point of view it is possible to explain more or less the phenomena of solidification processes, on some issues, there is a lack of clear answers regarding the understanding of the mechanisms of these processes at the atomic level. For example, it is not entirely clear what causes the release of latent heat and a jump-like decrease in volume during crystallization while in the case of amorphous substances solidification these phenomena are not observed.
Short description of a model
Today, there are a large number of computer simulation programs and advanced techniques that are used to reproduce various physical processes including of liquids processes solidification and crystallization [5-7]. But the use of sophisticated techniques and models requires a sufficient amount of computer resources and time consuming to deal with a large quantity of data, the analysis of which is extremely difficult, or even impossible. Since we were interested in the qualitative side of the process liquid solidification without taking into account its specific characteristics, we used a simple one-dimensional atomic model, the study of which was carried out by methods of molecular mechanics. Previously, the same model was used by Ya.I. Frenkel [4] in analyzing the stability of solids. In general, the potential energy of a discrete model is obtained by summing up the energies of N atoms, of which the model is composed
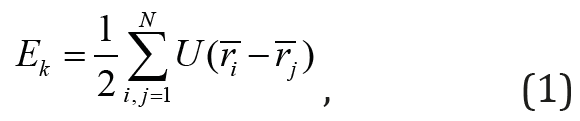
where 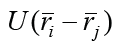 is the energy of the interaction of a pair of atoms
with coordinates riirj.
is the energy of the interaction of a pair of atoms
with coordinates riirj.
The energy of the interaction between two atoms was determined from the general equation:

where a =1, 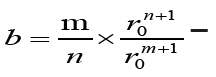 is constants,
is constants,
r is distance between atoms; r0 is equilibrium distance, when the minimum of the potential energy of interaction is reached; m and n are exponents for the energy of the forces of attraction and the forces of repulsion, respectively. Since the calculations are carried out to determine the qualitative characteristics of the model, the data in equation (2) are arbitrarily selected, but they are close to the values that are characteristic of real solids. In our case, we consider constant A and the exponent of m equal to one, and the exponent n = 8 and the equilibrium distance - r0 = 2.5 Å.
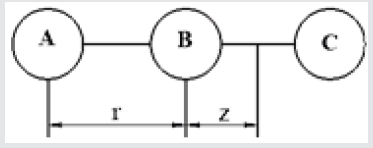
Three-atomic model: In the three-atomic model (Figure 1), the interaction energy of the average atom EA2 with two extremes 1 and 3 as the sum of the pair interaction with each of them was determined:
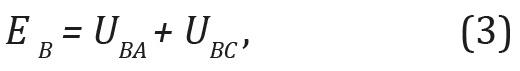
Where  is energy of the pair interaction of atom B with
atoms A and C;
is energy of the pair interaction of atom B with
atoms A and C;
In the case of the average atom displacement at a distance z (Figure 1), the energy of its interaction with atoms A and B is determined by
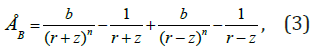
z - displacement of atom B relative to atoms A and C
The interaction energy of the middle atom EB with two utmost atoms A and B in the case of different temperatures was determined. The temperature change was modeled as an increase of the interatomic distance due to the action of the internal pressure of the atoms thermal motion. Three cases of changing the distance between atoms were considered r1 = r0 = 2.5 Å; r2 =3.1 Å; r3 =3.15 Å. The potential energy for one-dimensional models was also determined by equation (1). For the three-atom model, we considered two cases that differed in the nature of interatomic interaction. We considered the case of short-acting forces and longacting forces. (Interatomic interaction is characterized by a radius of action r¢ on which the attraction forces are small F < 0.1Fmax. For the radius r¢ ≈ r0, the forces are short-acting, when the radius r¢ >> r0 the forces are long-acting). In the first case, the energy of interaction between the nearest neighbors of the atom was considered, in the second - the interaction between the near and father neighbors of the atom. Additionally, the forces of interaction between atoms were calculated. The results of the calculations are presented in the form of graphs.
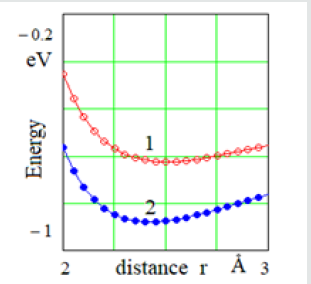
Figure 2: Change of the potential energy of average atom 2 when it is displaced z in the three-atomic model for the distance between atoms (Å) 1 - r = 2.5; 2 – r = 3.1 i 3 – r = 3.2
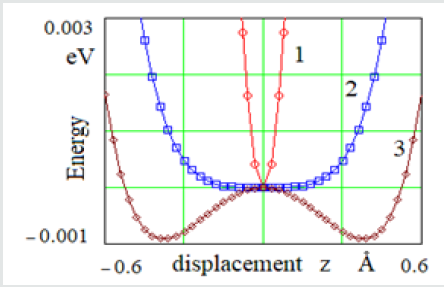
The potential of interatomic interaction with the shortacting forces Let us consider the change in the potential energy of atom B at different temperatures (Figure 2). The position of atoms at the equilibrium distance r = r0 = 2.5 Å corresponds to a temperature of 0 K (curve 1 in Figure 2). This position is stable, since the displacement z of the atom relatively atoms A and C leads to an increase in its potential energy. This is a solid state. At the interatomic distance r3 = 3.15 Å, the position of atom B becomes unstable due to the appearance of a “ridge” on the dependence curve of the potential energy change (Figure 2, curve 3). In this case, atom B will try to shift to either atom A or atom C. In a onedimensional model at this temperature, the atoms are grouped by two, and the interaction between such groups is reduced or is absent. This process can be seen as evaporation. At an intermediate temperature, when the distance between atoms is r2 = 3.1 Å (Figure 2, curve 2), the interatomic interaction is preserved. A flat bottom of curve 2 means that atom B can move freely between atoms A and C. So, it means that at this temperature, the one-dimensional model is in a liquid state. The potential of interatomic interaction with the long-acting forces of attraction If the interatomic interactions are long-range (r > 5 Å), the utmost atoms A and C also interact. Between them there is a force of attraction, which is balanced by repulsive forces between atom B and atoms A and C. In this case, the three-atomic model is compressed to r10 = 2.44 Å. In the case of short-acting forces, the interatomic distance r0 = 2.5 Å.The effect of compression of real crystals was mentioned earlier [8-10]. It has been experimentally discovered that the distances between the nearest neighbors are slightly shorter than the normal “own” diameter of the atoms [10].
Figure 3: Potential energy of three-atom model: 1 - interaction between nearest atoms; 2 – the interaction between of all atoms.
The interatomic distance r10 = 2.44 Å of the three-atomic model was calculated from the condition of the minimum value of the potential energy. The dependence of the potential energy of the three-atomic model on the interatomic distance for the case of the interaction of long-range atoms is represented by curve 2 on (Figure 3). The curve 1 in this figure reflects the same dependence, but for the case of the interaction only with near-neighbor atom. The differences between these energies are the latent crystallization heat. Thus, a jump-like decrease of the interatomic distance from r0 = 2.5 Å to r01 = 2.44 Å and the decrease of the potential energy (Figure 3) of the three-atom model is connected with the formation of the interaction between the utmost atoms. And this can be considered as a process of crystallization, for which release of latent heat and volume change is characteristic. It should be noted that in the case of short-acting forces, an amorphous body forms in the process of solidification. An indication of this is the absence of release of latent heat and volume changes. Let us consider the crystallization process in more detail, taking into account the interaction forces of atom C with atom B and A (Figure 4). At high temperatures, the distance between the atoms is bigger, as well as the high degree of mobility, so the atoms mostly interact with the nearest neighbors. As the temperature decreases, the distance between the atoms reduces, and the interaction between the utmost atoms increases. The strengthening of the interaction occurs at the some temperature. According to the graphs of the interaction between atoms (Figure 4), when the interatomic distance r1= 3.15 Å, the atom C is located to the right of the maximum of curve 1 (on figure 4 a position of the atom C is fixed and is shown by the vertical line passing through the point z = 0).
Figure 4: Dependence of the force interaction of atom 3 with atoms 1 and 2 at the interatomic distance: 1 – r1 = 3,2 Å; 2 – r2 = 2,5 Å.
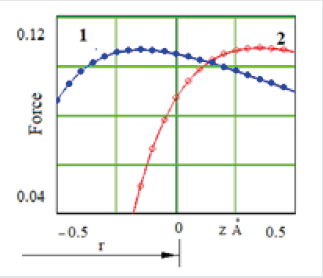
That position is unstable, since in the case of the displacement of atom C from its neighbors, the force of attraction decreases and the atom C will easily shift from due to the action of insignificant force. Therefore, this state of the three-atom model corresponds to a liquid state. When the interatomic distance is r2 = 2,5 Å (Figure 4, curve 2), atom C is at the left of the maximum of the curve of the dependence of the interatomic interaction. This is a stable state, since in the case of atom C moving away from the neighbors, the force of attraction increases, forcing the atom C to return to its previous position. Getting in the stable zone of the attraction forces of atoms A and B, the atom C “sucked” into the potential “pit”, to get out from which is problematic. This case corresponds to crystallization of a threeatom model. The described above mechanism of homogeneous crystallization can be used to eliminate the inconsistencies of the molecular-kinetic theory of crystals growth of V. Kosel and I. Stransky.
Conclusion
The tendency of liquids to solidify with forming a crystalline or amorphous structure depends from the properties of interatomic interaction potentials. In the case of short-acting potentials, atoms interact with their closest neighbors and form amorphous solids. If the interatomic interaction potentials are long-acting forces, atoms interact with their long-distance neighbors and form of crystalline bodies. When the interaction between atoms and their long-distance neighbors is formed, the potential energy of atoms is reduced again, and the latent heat of crystallization is released.
References
- Stephen H. Davis (2001) Theory of Solidification. Cambridge: Cambridge University Press.
- Cahoon JR (2013) On the nucleation rate for the solidification of metals. Canadian Journal of Physics 91(2): 140-145.
- Boiko VG, Mogel KhI, Sisoev VM, Chalyi AV (1991) Osobennost’ metastabil’nykh sostoyaniy pri fazovykh perekhodakh zhidkost’ - par [Peculiarity of metastable states during liquid - vapor phase transitions]. Uspekhi Fizicheskih Nauk 161(2): 77-111.
- Frenkel J (1984) Kinetic Theory of Liquids. Gloucester: Peter Smith Publisher.
- Xiong LH, Lou HB, Wang XD, Debela TT, Cao QP, et al. (2014) Evolution of local atomic structure during solidification of Al2Au liquid: An ab initio study. Acta Materialia 68(4): 1-8.
- Otajonov SH, Eshchanov BX, Isamatov AS (2011) Evolution of local atomic structure during solidification of Al2Au liquid: An ab initio study. Ukr. J. Phys 56(11): 1178-1181.
- Prasenjit Sen, Ciraci S, Buldum A, Batra Inder P (2001) Structure of aluminum atomic chains. Phys. Rev. B 64(19): 195420.
- Kozak LY (2016) Discrete Models of Plastic Deformation of Solids Under the Action of High Hydrostatic Pressure. Mater Sci 52(1): 108-112.
- Kozak LY (1999) Computer simulation of shifts of an atomic plane in a two-dimensional crystal lattice. Mater Sci 35(2): 132-135.
- Pearson WB (1972) The Crystal Chemistry and Physics of Metals and Alloys. New York (NY): Wiley-Interscience.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...