Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2641-6921
Mini Review(ISSN: 2641-6921) 
Calculation of the Hardness of a Multi-Element Equiatomic Metal Alloy Volume 2 - Issue 3
Zakarian DA* and Khachatrian AV
- Frantzevich Institute for Problems of Materials Science NAS Ukraine, Kiev
Received: December 20, 2019; Published: January 16, 2020
*Corresponding author: Zakarian DA, Frantzevich Institute for Problems of Materials Science NAS Ukraine, Kiev
DOI: 10.32474/MAMS.2020.02.000136
Abstract
A phenomenological approach has been developed for the mathematical description of the hardening of high-entropy alloys (HEAs) and a quantitative assessment of their hardness. It is shown that in HEAs with a bcc lattice, the degree of hardening is always greater than in HEAs with a fcc lattice (with the same number of elements in alloys). To calculate the relative hardening of the alloy, the type of crystal lattice and its parameter value are required. The calculation results are consistent with experimental data. Basic parameters of HEAs are calculated from first principles. The proposed method can be considered acceptable for assessing the hardness and degree of hardening of multi-element alloys (HEAS).
Keywords: Multielement alloys; energy of interaction of elements; mismatch parameter; distortion density; hardness; heas
Introduction
One of the most common characteristics that determine the
quality of metals and alloys, the possibility of their use in various
designs and under various working conditions, is hardness.
Hardness tests are performed more often than determining other
mechanical characteristics of metals: strength, elongation, etc.
A specific method for determining hardness is selected based on
the properties of the material, measurement tasks, conditions
for its implementation, available equipment, etc. Hardness is a
technical characteristic of a material, and depends on a set of
physical properties, such as: interatomic distances, coordination
number, number of valence electrons, nature of the chemical
bond, brittleness, elasticity, viscosity, etc. And calculation it from
first principles without taking into account experimental data at
the present stage is impossible, especially if this applies to multielement
or high-entropy alloys (HEAs).
It is generally accepted that one of the fundamental concepts
for a HEAs is that the lattice structure of a solid solution is greatly
distorted. The displacement of atoms from their ideal positions is
given as the reason for the manifestation of a number of observed
physical and mechanical properties. It is believed that the distortion
of the crystal lattice of the HEAs creates an obstacle to the free
movement of dislocations, i.e. serves as a deterrent to plastic
deformation. Therefore, to describe the hardening of the HEAs, the
main emphasis in the research is placed on taking into account the
difference in the radii of the atoms present in the alloy. Basically,
the mean quadratic displacement of atoms from the equilibrium
position in an ideal, undistorted lattice is used as a mismatch
parameter [1,2].
In [1], it was found that the normalized strength at 0 K for
8 fcc alloys, five-element equiatomic HEA CrMnFeCoNi and its
derivatives is proportional to the mean square displacement. Thus,
arguing that the root mean square displacement are an important
factor in predicting the yield strength of alloys at 0 K. For the same
alloys in [2], from the results of experimental studies it was found
that not always an increase in distortion necessarily leads to an
improvement in physical characteristics. Those. in assessing the
mechanical characteristics of a HEAs, it is necessary to take into
account not only the parameters of the mismatch of atomic radii,
but also the values of the interaction potential of different elements.
Here it is appropriate to cite the statement of the authors of [3],
who believe that at present there is no clear evidence that the lattice
distortions in the HEAs are much higher than in conventional alloys.
Another method for assessing hardening in HEAs is solid solution
hardening, where Fleischer, Lyabush and Gippen approaches are
used, which are mainly used for binary alloys [4].
The vast majority of works are methods that work well on some
HEAs and much worse on others. The mechanism of strengthening
the HEAs is the most important feature of this class of materials and this issue, so far, has neither a clear explanation, nor fundamental
confirmation. The main emphasis is on creating barriers to the
movement of dislocations and, less commonly, on the features of
the interaction of dissimilar atoms with each other. Undoubtedly,
the asymmetric environment of each of the atoms in the crystal
of a disordered alloy leads to the fact that the equilibrium state
of the alloy is accompanied by the appearance of distortions of its
crystal lattice. These distortions depend only on the composition
of the alloy; they do not arise and do not disappear during the
thermomechanical treatment. In this paper, we propose a “hybrid”
method - a combination of first-principle methods, the use of
experimental data (relating to pure metals) and a phenomenological
approach to assess the hardness of a HEAs with a bcc and fcc singlephase
structure.
Calculation of Basic Parameters of a HEAs
To calculate the basic parameters of a HEAs, an a priori
pseudopotential is used [5].When studying the properties of
transition metals using the pseudopotential method, the state of
d electrons is taken into account, which occupy an intermediate
position between highly localized internal states and free electrons
in the crystal. The interaction of d electrons with conduction electrons leads to the appearance of two additional terms in the
pseudopotential of the ion associated with the overlap of s and d
waves and with the resonant interaction of d waves. We consider
the case when the system consists of different metal atoms with
concentrations 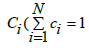 forming an alloy of the substitution type.
The pseudopotential of the alloy is determined according to
the conditions of its additive nature
forming an alloy of the substitution type.
The pseudopotential of the alloy is determined according to
the conditions of its additive nature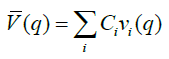 where vi(q) is the
pseudopotential of the i-th ion.
where vi(q) is the
pseudopotential of the i-th ion.
Note that in high-entropy alloys, quantum-mechanical calculations are carried out in the same way as for pure metals, but with an average pseudopotential of the form [1]. The energy of the electron-ion system is calculated using the perturbation theory in pseudopotential up to second order inclusive. In order to evaluate the hardening of multi-element alloys by theoretical methods, it is necessary to study the mechanical behavior of an increasingly complicated sequence of alloys related in composition. Using an a priori pseudopotential [5], for pure metals and alloys with an fcc and bcc structure, the type of crystal structure, lattice parameters, and elastic moduli for the family of equiatomic nickel CrMnFeCoNi HEAs are determined from the minimum energy. The calculated data are consistent with experimental data [6,7] (Figure 1) Table 1.
Figure 1: Lattice parameter of multi-element alloys with bcc and fcc lattices and their experimental values (2, 7, 9). R2 is the coefficient of determination
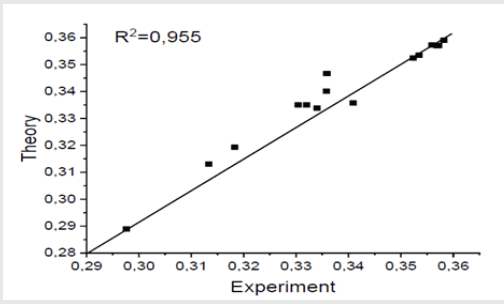
Table 1: The calculated (Eс) and experimental (Eex) values of the elastic moduli of Ni based alloys (in GPa).

As for the mean square displacement, paired interatomic potentials are used to determine it. If we calculate the pair interactions for any two atoms in the alloy (i.e., surrounded by random types of atoms), then the result will be the same for all pairs of atoms, because the interatomic distance is determined using the average lattice parameter. Therefore, to determine the interatomic distance of different types of atoms, we carry out calculations for alloys consisting of two types of atoms. To determine the distances between atoms of the same type, calculations are carried out as for pure metals. Theoretically, it is possible to evaluate the influence of any new element on the characteristics of the selected element in the alloy. To assess the mechanical characteristics of the HEAs, averaged basic parameters are used, such as the lattice parameter, atomic radius, and root mean square displacement [8].
Modeling the Structure and Properties of HEAs, Calculation Results and Discussion
We model the structure of a HEA with n elements. Depending
on the type of crystal lattice, for a complete description of
the
structure of the HEAs, it is necessary to take into account:
a. The number of unit cells where pair interactions are realized,
both between the same type and the different type elements.
b. The number of unit cells, which takes into account the
diversity of the population of atoms (taking into account the
concentration ratio).
The number of obtained unit cells depends not only on the type of crystal lattice, but also on the number of elements. A set of these elementary cells can be represented as an “abstract, virtual particle” possessing the properties of a HEA and containing the basic elements of its structure. For example, in a three-element alloy (n = 3), 12 unit cells are sufficient to describe the properties and structure, if the alloy has an fcc lattice, and in the case of a bcc lattice, there are 6 cells in which atoms of different sorts are randomly distributed, exhausting all possible distribution options. The set of these unit cells is sufficient for calculating the basic parameters of the alloy from first principles. The totality of these unit cells carries information about the property and structure of the alloy. The selected group with a certain number of elementary cells of the HEA is sufficient for the mathematical description of the basic properties and structure of the alloy.
The volume of the “particle” can be estimated by the formula Ωx = N.Ω , where N is the number of unit cells, the combination of which represents the “characteristic particle”, Ω is the average volume of the unit cell of the alloy. The linear particle size will be d = (N.Ω)1/3 .
We introduce the concept of distortion density, which is directly proportional to the distortion Δr and inversely proportional to the linear size of the “particles” ρ = Δr / d . We use the main feature of the HEAs - the distortion of the crystal lattice, as a deterrent to plastic deformation and the movement of dislocations.
Our task is to use this feature of the HEAs without affecting the mechanism of movement of dislocations in the HEAs. Those, we are modeling not the process of inhibition of dislocation motion, but the consequence of this process is the hardening effect. An increase in the distortion density, i.e., a decrease in the effective size 1 d1 = 1/ρ, leads to an increase in the force that impedes the propagation of plastic deformation and to hardening of the material. In this context, a HEAs can be described as a “polycrystalline” material consisting of “particles” or “grains”, at which “boundaries” inhibit the movement of linear defects and, accordingly, harden the material. In this case, the degree of distortion of the crystal lattice or “distortion density” acts as a boundary. In this regard, the strengthening of the HEAs can be estimated by analogy with the Hall-Petch law in the form:
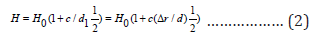
where H0 = ΣCiHi is the average alloy hardness, estimated according to the rule of the mixture (Hiis the hardness of a single crystal consisting of the i-thelement included in the alloy),c is the material constant, which is proportional to the number of elements included in the alloy. As for distortion, it is possible to use different versions of its representation [6]. Based on the results of a computational experiment, the most unambiguous, therefore, successful option is to present the distortion in the form Δr = rmax − rmi (rmaxand rminare the maximum and minimum atomic radii of the elements in the crystalline modification of the alloy). Given that the unit cell volume Ω=a3(а is the lattice parameter), we obtain:
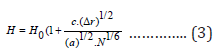
With an increase in the number of types of atoms, the distortion of the crystal lattice increases. Using relation (3) for substitutional type alloys (NiCo) and comparing the calculated and experimental data on hardness, we find that c = 3.8 n (n is the number of elements in the alloy). For a relative increase in hardness, we obtain
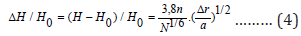
The relative increase in hardness depends on the ratio of the parameter Δr to the crystal lattice parameter of the alloy a. If the first factor is related to the difference in atomic radii of the elements, then the second is indirectly related to the potentials of different elements, as well as their interaction. Formula (4) takes into account the effect on the mechanical characteristics of the distortion of the crystal lattice.
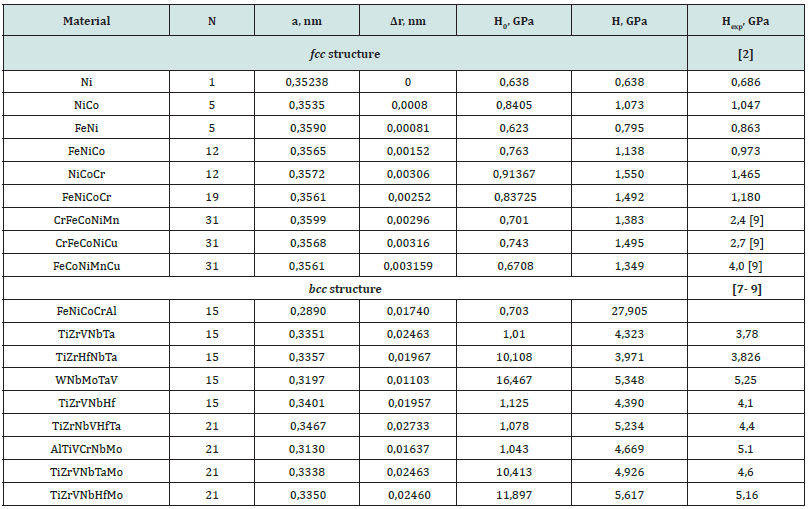
A computational experiment was carried out for a HEAs with an fcc lattice, mainly for an equiatomic HEA Minecon and its derivatives with nickel, as well as 5 and 6 element equiatomic alloys with a bcc lattice. All alloys have a stable single-phase structure. The average difference in the atomic radii of the elements (which are part of the alloy) from the average radius of the alloy is not more than 6.6%. From the results obtained Table 2, it follows that using the relation (3), it is possible to evaluate the hardness of various multi-element, including two-element and three-element metal alloys. The experimental values of hardness taken from [9] for fcc alloys are overestimated in comparison with the calculated values. But, as noted in [9], in these alloys, in addition to solid solutions of HEAs based on fcc lattices, solid solutions based on bcc lattices, as well as intermetallic compounds, can be present. In other cases, the results of the experiment and calculation are close. If we compare the hardness values of the equiatomic HEA CrFeCoNiMn and its derivatives with the presence of nickel with an elastic modulus Table 1, we see that there is a direct relationship between the elastic modulus and hardness for some alloys when the number of elements in the alloy is n ≥ 3. As shown calculation results and experimental data [9] there is not always direct proportionality between the elastic modulus and hardness in both bcc and fcc HEAs.
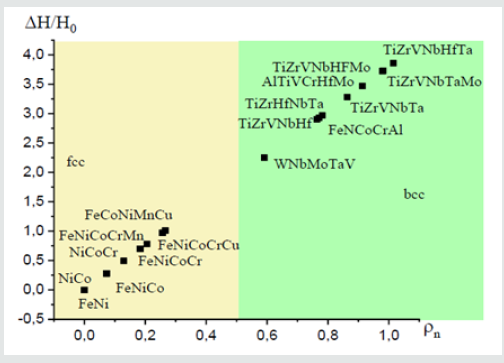
We estimate the relative increase in hardness. Following
relation (4), we present the relative increase in hardness ΔH/H0 of
alloys as a function of the parameter 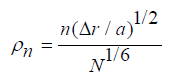 of fcc and bcc alloys in (Figure 2). The left part of the figure shows the results of calculating
the increase in hardness as a function of the parameter ρn for nickelbased
alloys consisting of two, three, four and 5 elements having an
fcc structure. An increase in ρn leads to an increase in hardness. The
greatest effect of hardening of solid solutions from equiatomic HEA
of CrMnFeCoNi and its derivatives with the presence of nickel with
an fcc structure is observed in a 5-element alloy (FeNiCoCrMn),
slightly lower than a 4-element alloy (FeNiCoCr), when the first
place in terms of hardness in this family NiCoCr. The right part of the
figure shows the results of hardening for bcc alloys. A comparison
of the relative strengths of the HEA shows that HEAs with a bcc
lattice are stronger than the alloys with an fcc lattice, provided that
the number of elements in the alloy is equal. This confirmation also
follows from formula (4). Even if
of fcc and bcc alloys in (Figure 2). The left part of the figure shows the results of calculating
the increase in hardness as a function of the parameter ρn for nickelbased
alloys consisting of two, three, four and 5 elements having an
fcc structure. An increase in ρn leads to an increase in hardness. The
greatest effect of hardening of solid solutions from equiatomic HEA
of CrMnFeCoNi and its derivatives with the presence of nickel with
an fcc structure is observed in a 5-element alloy (FeNiCoCrMn),
slightly lower than a 4-element alloy (FeNiCoCr), when the first
place in terms of hardness in this family NiCoCr. The right part of the
figure shows the results of hardening for bcc alloys. A comparison
of the relative strengths of the HEA shows that HEAs with a bcc
lattice are stronger than the alloys with an fcc lattice, provided that
the number of elements in the alloy is equal. This confirmation also
follows from formula (4). Even if 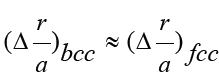 then for equal amounts
of elements in the two alloys, the coefficient
then for equal amounts
of elements in the two alloys, the coefficient 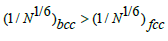 which
means that the distortions density is higher in the bcc HEAs than
in the fcc.
which
means that the distortions density is higher in the bcc HEAs than
in the fcc.
Table 2: The calculated values of the lattice parameter (a), the maximum difference in atomic radii (Δr), the average value of the alloy hardness (H0), the hardness for different metal alloys with bcc and fcc structure (H) and their experimental values (Hexp).
It is generally accepted that a model adequately describes a
physical process if it obeys two conditions:
a. Physically justified.
b. The calculation results have experimental confirmation.
The proposed model satisfies these two conditions.
In all used methods (approaches), it is believed that the
mechanical characteristics are directly proportional to distortions
(mismatch of atomic radii of the elements). However, not all
alloys obey this ratio. In our proposed model, in fact, physical
characteristics are proportional to distortion to the degree of ½.
This approach allows to comprehensively take into account the
features of the distorted crystal lattice of HEAs when assessing
their physical and mechanical characteristics. It follows directly
from relation (4) that for any two-element alloy of the substitution
type, the relative hardening is always less than that of any threeelement
single-phase alloy, even if Δr of the two-element alloy is
greater than that of the three-element one
Summary
For hardening, the number of elements included in the composition of the alloy, the type of crystal lattice and the density of distortion are of key importance. The last parameter depends on both the mismatch parameter and the interatomic interaction potential. The role of the phenomenological approach is the mathematical description of the inhibition of plastic deformation. As a braking force in HEAs, the concept of “grain size” is used, which is defined using a set of unit cells, which is a carrier of informationthe properties and structure of a multi-element alloy. The proposed method, using experimental information on the hardness of metals, can be considered acceptable for assessing the hardness of multi-element alloys (HEAs). The resulting analytical formula is of practical importance, because makes it possible to evaluate the degree of hardening for any single-phase equiatomic HEA, if the experimental data of the alloy are known - the type of crystal lattice and its parameter.
References
- Norihiko LO, Koretaka Y, Katsshi T, Haruyuki I, Easo PG (2016) Atomic displacement in the CrMnFeCoNi high-entropy alloy-A scaling factor to predict solid solution strengthening. AIP Advances 6(2):12008.
- Wu Zhenggang (2014) Temperature and Alloying Effects on the Mechanical Properties of Equiatomic FCC.Solid Solution Alloys. University of Tennessee, Knoxville.
- Lewis RO, Nicholas GJ (2018) Lattice distortions in high-entropy alloys. J Mater Res 33(19): 2946-2969.
- Isaac TodaCaraballo, Pedro EJRDC (2015) Modelling solid solution hardening in high entropy alloys. Acta Materialia 85: 14-23.
- Zakaryan DA, Kartuzov VV, Khachatryan AV (2015) Calculation of the basic physical and mechanical characteristics of highly entropic metal alloys.Mathematical models and computational experiment in materials science 17: S78-82.
- Khachatryan AV (2018) Physical characteristics of equiatomic Nickel alloys and their relationship with distortions. Mathematical models and computational experiment in materials science20:S115-120.
- Firstov SA, Rogul TG, Krapivka NA, Ponomarev SS (2013) Effect of crystallization rate on the structure, phase composition and hardness of the high-entropy AlTiVCrNbMo alloy. Deformation and destruction of materials 10: C8-15.
- Gorban VF, Krapivka NA, Firstov SA, Kurylenko DV (2018) The role of various parameters in the formation of the physicomechanical properties of high-entropy alloys with a bcc lattice. Physics of metals and materials science119(5): 504-509.
- Report III-6-16 (2018) NASU. Regularities of the formation of solid solutions with bcc and fcc lattice in high-centropium alloys and the influence of various factors on the phase, state, structure and physico-mechanical properties.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...