The Paradoxes of Speed from Herodotus To Einstein Volume 3 - Issue 4

Patrice F Dassonville*

• Former Director of Le Mans Faculty of Science and Technology, France

Received:July 18, 2019;   Published: July 29, 2019

*Corresponding author: Patrice F Dassonville, former Director of Le Mans Faculty of Science and Technology, France

DOI: 10.32474/PRJFGS.2019.03.000168

 

Abstract PDF

Abstract

The Phoenician, Persian, Greek, Roman sailors and strategists brought out the notion of velocity in the middle of the first millennium BCE. Velocity results from an archaic intuition of a relation between space and time. The progressive evolution of its uses was going to be shaken by the Newtonian formalization, and afterwards by the outbreak of relativity early twentieth century. It makes this concept worthy of attention.

Keywords: Time; Space; Days’ Walk

Introduction

The study of geo-historical origins highlights how speed was invented, including the first speed units. It also shows the way of defining the concept. The English physicist Isaac Newton (1642-1727) will formalize the mathematical relation between space, time and speed, however it won’t prevent sophisms such as the speed of time. The value of the speed of light is expressed in relation to the « meter » and the « second », and considered a fundamental constant: then, can the « meter » be defined using the speed of light? The gradual complexification of physical laws leads to wondering what speed has become with the implementation of the laws of special relativity.

The Outset of Speed

In « The Histories », the Greek historian Herodotus (484-425) frequently specifies the distances travelled (or to be travelled) by using « days’ walk », « days’ sail » or « months’ sail » (Book II, 19 and 31: « The distance is not short: it’s three days’ walk » (Book III, 6). In « The Peloponnesian War », the Greek father of History, Thucydides (c.465-c.395) explains that a man would need « eleven days of walking » from Abdera to the Istos; and he emphasizes « that is the length of the coasts » (II, 97). In « Anabasis », the Greek historian Xenophon (c.428-c.353) reports that Cyrus’s enemy was on the banks of the Euphrates at twelve « days’ walk » (Book I, Ch. III). In « Parallel Lives », the Greek biographer Plutarch (c.46-c.125) writes that the Greek Timoleon (c.410-c.337) decided to deploy his army at eight « days’ walk » from Syracuse (Life of Timoleon, 25, 5). Considering how slow walking armies could be, for Persian, Greek, and Phoenician strategists, and especially for the foot soldiers and sailors who actually carried out these maneuvers, « days’ walk », « days’ sail » and « months’ sail » had the advantage of indicating both the distance and the travel duration. « walk in one day » was the average distance walked in one day by troops of that time; « sailing in one day » was the average distance of navigation done in one day; « sailing in one month » was the average distance of navigation done in one month. They can be considered as the first speed units of moving. So much so that, for the Persian generals in charge of leading their motley crowd to Greece, the rate of progress of the army was a basic parameter, a crucial constraint, rather than a consequence. The speed of armies was the same for Athenians, Spartans, Macedonians, Lydians, and Egyptians. For strategists, it was a kind of fundamental constant, equivalent to approximately 30 km per day, and less than 25 km per day in the case of a retreat, according to Herodotus. These data are confirmed by Xenophon who successfully organized the famous « retreat of the ten thousand », the Greek mercenaries in the service of Cyrus; Cyrus had been defeated by his brother Artaxerxès II, the king of Persia (Book I, Ch. II).

Nowadays, this impressive association of distance and time is formalized in the equations:

DAYS’ WALK = (DISTANCE WALKED IN ONE DAY) x (NUMBER OF DAYS)

DAYS’ SAIL = (DISTANCE SAILED IN ONE DAY) x (NUMBER OF DAYS)

MONTHS’ SAIL = (DISTANCE SAILED IN ONE MONTH) x (NUMBER OF MONTHS)

The Michelin maps of Sahara desert warn travellers about the fact that distances in kilometers are displayed only for guidance: even today, a distance expressed in « hours’ walk » or « hours’ drive » and a speed expressed in « distance driven in one hour or in one day » are much more informative for explorers. Velocitas is used by the Roman general Caesar (101-144): « pedites velocissimi » for « the fastest infantrymen »; and the Latin scholar Cicero (106-43): « nihil est animo velocius » for « nothing is faster than mind ». The Latin rhetorician Fabius Quintilius (1st century CE) uses « velox navigatio » for « quick navigation »[1]. Plutarch reports that during a fight against barbarians, the Roman dictator Sylla (138-178) shortened the space between his army and the barbarians, thanks to the velocity of his troops (Life of Sylla, 18, 4). In « De rerum natura » the Latin scholar Lucretius (c.95-55) explains that bodies are moving in the vacuum at the same speed, whatever their weight (Song II, 238). Unfortunately, he does not say what experiment led him to this right statement. Broadly speaking, Lucretius provides a great deal of information that may delight a current physicist. For example, the notion of acceleration was known, but it was not conceptualized; he writes that « lightning must acquire speed again and again, speed which keeps increasing all along the way » (Song VI, 341).

First Definitions

According to Herodotus « the walking speed is what is walked in one day », « the sailing speed is what is sailed in one day or in one month. Herodotus and Xenophon state that in case of retreat the walking speed drops from the equivalent of 30 km per day to less than 25 km per day. Thanks to Thucydides the length of the coasts can be roughly measured in relation to a speed unit (the day of walking): the « length of the coasts corresponds to eleven days of walking ». Plutarch allows one to rough out a definition: « the velocity is an effective way to shorten space ». Lucretius mention an important property, « bodies fall at the same speed ». Furthermore, he allows us to roughly define the acceleration as « the increase of speed ».

Newton’s Formalism

It was not until Newton arrived on the scene that this was formalized [2] by:

DISTANCE TRAVELLED = VELOCITY x DURATION OF THE TRAVEL

that is written in abbreviated words:

d v x t

where « t » denotes time indicated by a clock.

The Newtonian formalism completely revolutionized the physics of the day, but it also introduced an insidious ambiguity: indeed, a « field model effect » suggests that time is an active factor in the distance travelled, whereas in fact « t » is just the indication of a clock. Speed is the only active factor in the motion: we can add that speed is the ability to move, the capacity of changing location. If « v » equal zero, no change is possible.

The Speed of Time

In « Odes », the Latin poet Horace (65-8 BCE) asserts that « fugaces labuntur anni! » (years pass quickly!) (Book II, XIII). In « As you like it » (1599) the English dramatist William Shakespeare (1564-1616) makes Rosalind say: « Time travels in divers paces with divers persons » (Act III, Scene II). The word « heterochrony » now designates the illusive heterogeneity of durations. Unfortunately, asserting that time passes quickly or that it flows slowly, is assigning time a speed, but with respect to time, which is a sophism. Instead of that, they are events that happen more or less quickly. Nowadays it is often referred to « time of biology», to « time of history », to « the longtime of geology », to « the long time in the evolution of the Universe », to « time in the evolution of species », etc. in order to assert that there are several kinds of time, depending of the field of research. It’s obviously wrong because all of these expressions designate events, changes, evolutions - fast or slow - but never time.

The Speed of Light

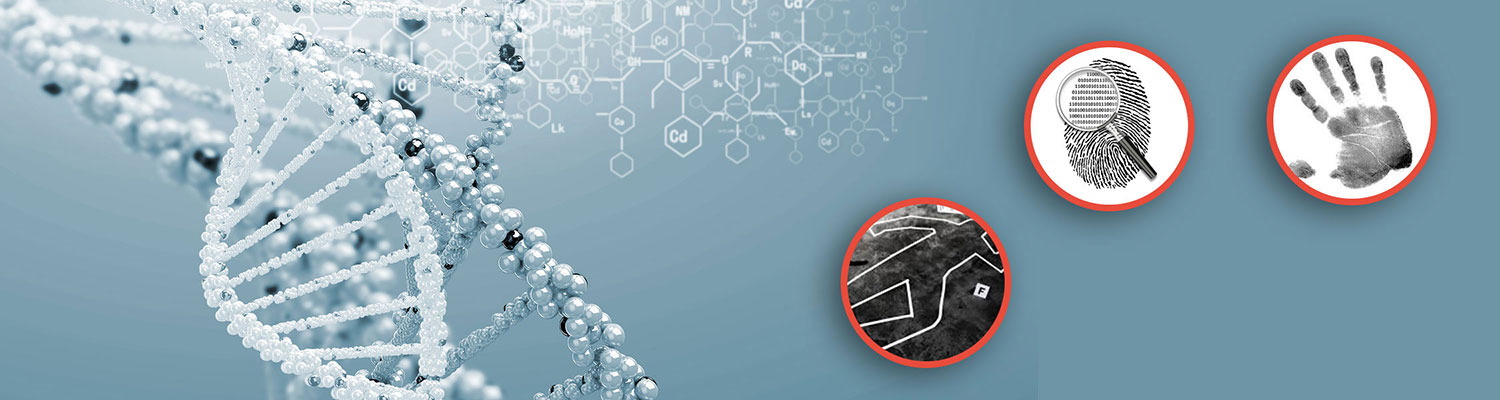
In « Astronomie Populaire » (1881), The French Astronomer Camille Flammarion (1842-1925) reminds some results of measurements: 315 000 km/s by Fizeau in 1849; 298 000 km/s by Foucault in 1850; 300 400 km/s by Cornu in 1874 (Book III, Ch. 7) [ 3]. After a long diachrony of the value of the speed of light in the vacuum, the Conférence Générale des Poids et Mesures of 1983 [4] decided to agree on the exact value of the fundamental constant:

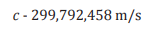
The 2018 Conference confirms its decision, and in the wake, declares « (the meter) is defined by taking the fixed numerical value of the speed of light in vacuum c to be 299 792 458 when expressed in the unit m/s ». The speed of light is expressed in relation to the meter, and in the wake, the meter is defined in relation to the speed of light: it looks like a sophism.

The cesium frequency is a fundamental constant equal to 9 192 631 770 Hz; its wavelength is:

Then the meter is expressed compared to the wavelength of cesium:

Hence a consistent definition:

« The meter is equal to (9 192 631 770/299 792 458) times the cesium wavelength ».

The expressions « fundamental constant », « constant of physics » and « physical constant » are more suitable than « constant of the nature » and « constant of the Universe » for a simple reason: the constants are not pre-existing in the Universe, instead they result from measurements and calculation, and the ultimate decision of the Conference in the particular case of the speed of light.Instead of « m/s », the international unit of speed could be assigned its own name, that would put an end to its alienation to space and time: by replacing « m/s » by « cel », « c » would read

« cel » for « celerity »; « célérité » in French; from Latin « celer »: fast. Plutarch reminds that Celer, the Romulus assistant, was commanding the Celeres (the Rapids), the three hundred guards of Romulus (Life of Romulus, 10. 2).

The Light-Year

Nowadays, astronomers use the light-year, among other units of distance: it’s the distance travelled by light (and broadly speaking, by electromagnetic waves) in one year. The light-year results from a similar approach as above: this double unit indicates both the distance of the object and the time taken by light to reach us, and it thus indicates the age of the object in the image we make: the delay is

t - d/c

Flammarion explains why astronomical images are delayed by reason of limitation of speed of light; he gives the example of solar flares which are observed 8 minutes after their triggering (Book IV, Ch. I). The light needs eight minutes to reach us; the images received are old eight minutes.

The star Proxima Centauri, the closest star to the Sun, is located a little more than four light years: therefore, the star is observed where it was and like it was four years ago. Unlike what is commonly asserted, it is not at all about a return in time.

The Relativistic Speed

Let’s observe an object whose speed is close to that of light: among parameters received in the laboratory, its length looks smaller (space contraction), durations look longer (time dilation), etc. however lengths and durations keep the same values in the object. These values are modified during the travel between the object and the laboratory for two reasons: high speed of the object relative to the laboratory and information propagated at the speed of light. The parameters are no more invariant, the laws of classical mechanics are no more valid; they must be replaced by the laws of special relativity, in order to get rid of the covariance and collect the exact data. In classical mechanics the speeds add up and retrench: two individuals walking in opposite direction, at respective speeds « v’ » and « v’’ », are moving away from each other at the speed

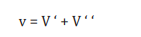
When speeds are close to that of light, calculations must be done using the transformation of Lorentz [5]:

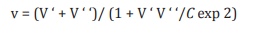
. Example: two photons (particle associated with light) in opposite direction (v’ = c and v’’ = c) are not moving away from each other at speed « 2 c ». We replace « v’ » and « v’’ » by « c »; the result is « v = c ». Hence the idea of « mathematical curvature of space-time »; « mathematical », given that « space-time » has no physical existence.

. Example: two particles in opposite direction at « v’ » and « v’’ » equal to « c/2 »: the result is « v = 0.8 c » instead of « c ».

. Example: light emitted by headlamps of a car travelling at the speed « v’ » relative to the road; the speed of the photons relative to the car « v’’ » is « c ». The speed of the photons relative to the road is not « v’ + c » but « c ».

. Example: if « v’ » and « v’’ » are much smaller than « c »,

v’ v’’/c exp 2 # 0

therefore

In # V ‘ + V ‘ ‘

It emerges that the classical modelization is a particular case of the relativistic modelization.

Conclusion

The notion of velocity came from the needs of walkers, sailors and strategists of knowing their mobile capacity with a greater accuracy, and therefore their potential advantages. Simple and elementary at its early stage, the speed became a central parameter in all dynamic phenomena, with an increasing complexity as can be seen from the laws of relativity. Paradoxically, physics did not give it a proper unit, although the speed of light is a fundamental constant.

References

1. Gaffiot F, Flobert P (2012) Le Grand Gaffiot. Hachette Paris.
2. Klein E (2003) Chronos Tactics: Flammarion Paris.
3. Flammarion C (1881) Popular Astronomy :Flammarion Paris.
4. General Conference of Weights and Measures: General Conference on Weights and Measures.
5. Mavrides S (1988) Relativity University Press of France.