The Scaling Law for Resistance of a Wearable Fabric Sensor: Fractal Analysis and Experimental Verification Volume 4 - Issue 3

Yu-Ting Zuo^1,2*

• ¹School of Materials Science and Engineering, Lanzhou University of Technology Lanzhou, PR China
• ²State Key Laboratory of Advanced Processing and Recycling of Non-ferrous Metals, Lanzhou University of Technology, PR China

Received:August 24, 2021   Published: September 07, 2021

*Corresponding author: Yu-Ting Zuo, School of Materials Science and Engineering, State Key Laboratory of Advanced Processing and Recycling of Non-ferrous Metals, Lanzhou University of Technology Lanzhou, PR China

DOI: 10.32474/LTTFD.2021.04.000186

Abstract PDF

The resistance formulation for a metal conductor is well-known to all students. It scales with the ratio of its length to the square of the radius. For non-metal conductors, e.g., a wearable fabric sensor, this formulation becomes totally invalid, and a fractal modification has to be adopted. This paper employs the two-scale fractal theory to establish a scaling law for the resistance of a carbon-based sensor material for smart fabric applications, and an experiment is carried out to verify the new formulation.

Keywords: Graphene-based Composites; Two-scale Fractal Dimension; Scaling Law; Carbon

The resistance property of a conductive wearable fabric sensor is the most important in smart fabric applications, especially in continuous health monitoring [1]. The resistance calculation is far different from that for a conductor. A conductor is the cornerstone in the fundamental theory of circuit and its resistance can be calculated by the following formulation

where R, λ, and r, respectively, the resistance, the length and the radius of the resistor, k is a material constant. Eq. (1) can be written in two scaling laws:

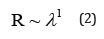
and

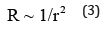
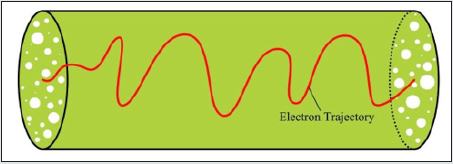
The scaling law of Eq. (2) can be explained as the straightline transmission, see Figure 1(B), the exponent of 1 implies the dimension of the straight line. The scaling law of Eq. (3) implies that electrons are occupied on the whole section with the dimension of 2, see Figure 1(A).

Figure 1: Resistance for a metal conductor.

Eq. (1) is valid for metal resistors, for non-metal ones, Chinese mathematician, Dr. Ji- Huan He, suggested a scaling law to calculate the resistance [2-4]:

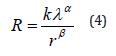
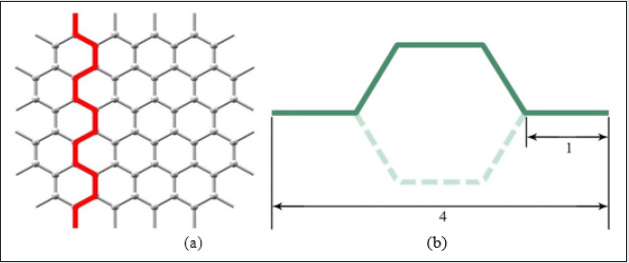
where α is the fractal dimension of the electron trajectory as illustrated in Figure 2, β is the fractal dimension of the section, α=1 for a metal conductor, see Figure 1(B). We assume that there are many electrons occupied in the section, as illustrated in Figure 1(A), the continuum section for a metal conductor leads to β=2. For the surface resistance like that in the electrospinning process, β=1, see Figure 3; Eq. (4) can be written in two scaling laws:

Figure 2: The transmission trajectory of charges.

Figure 3: Resistance for surface convection.

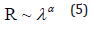
and

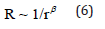
The scaling law of Eq. (5) can be explained as the non-straightline transmission of charges, the exponent of α is the two-scale fractal dimensions of the curve line of the charge transmission, see Figure 2. The scaling law of Eq. (6) implies that electrons are occupied partly on the section with the two fractal dimensions of β. Consider a charged jet in an electrospinning process, see Figure 3, the current due to the surface convection of the charges can be written as [5,6]

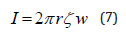
where I am the surface current, ζ is the charge density per length, w is the charged jet’s velocity. When the surface charge is negative, the current direction follows the charged jet’s motion, however, when the surface charge is positive, the current direct is opposite the jet’s motion. Eq. (7) implies that

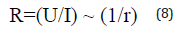
where U is the applied voltage on the charged jet. Eq. (8) meets the scaling law of Eq. (6), for the section is two dimensional and its boundary of its perimeter is one dimensional (Figure 4).

Figure 4: Graphene’s geometry (a) and its unit (b).

The formulation for calculation of the two-scale fractal dimensions is as follows [7-10]

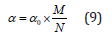
where M/N is ratio of the measured units under two scales, and α0 is dimensions for large scale. For example, the two-scale fractal dimensions for the Koch curve is 4/3=1.1333 instead of the Hausdorff fractal dimension of ln4/ln3=1.2618. The Hausdorff fractal dimension is for strict fractal patterns, while the two-scale fractal dimension is used to figure out the porosity and unsmooth boundary. The two-scale fractal theory has been widely used as an effective mathematics tool to analysis of various discontinuous problems, for examples, the fractal rheological law [11,12] the fractal oscillator for 3D printing technology [13], the fractal mechanical and electrical properties of graphene/sic composites [14,15], the time-fractional Kundu- Mukherjee-Naskar equation [16], the fractal diffusion law [17], the fractal two-phase flow model18, the fractal convection-diffusion law, and Fangzhu’s water collection from air [19-22].
In this paper we will study the scaling law for resistance of a lead of a pencil, which consists mainly of graphene. Consider a unit of the graphene as illustrated in Figure 4(B), we have M/N=5/4 and a0 = 2 , so we have

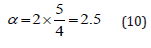
According to Eq. (5), the resistance of a carbon nanotube can be expressed as

where μ is a constant, L is the length of the lead.

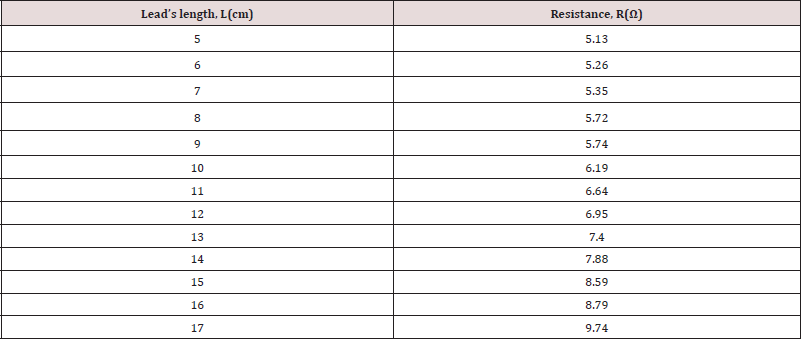
In our experiment, Chung Hwa Drawing Pencils (China First Bengbu Pencil Co., LTD.) with 2B type and the Fluke insulation resistance measuring instrument (Model no. 1508, Fluke Corporation, USA) were used to measure the lead’s resistance with respect to its length, see Figure 5. The experimental data were given in Table 1. Consider the contact resistance in the measuring process, we write Eq. (11) in the form

Figure 5: Pencil and insulation resistance meter for experiment.

Table 1: Experimental data.

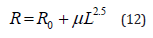
where R0 is the contact resistance.

By the least square method, using the experimental data given in Table 1, we can identify

So, the lead’s resistance for our experiment is

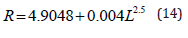
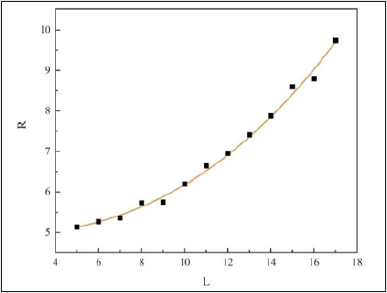
The theoretical prediction sees good agreement with the experimental data as shown in Figure 6. Figure 6 Resistance (Ω) versus length (cm) for a pencil’s lead. The dots are experimental data, the continuous line is the theoretical prediction by Eq. (14).

Figure 6: Resistance (Ω) versus length (cm) for a pencil’s lead. The dots are experimental data, the continuous line is the theoretical prediction by Eq. (14).

This paper uses a widely used carbon-based material for pencils to verify the scaling law of the resistance, which can be applied for wearable fabric sensors for various applications especially in smart fabrics. The experimental results verify that pencil’s lead consists mainly of graphene with a fractal dimension of 2.5. This paper is helpful for study of the electronic property of graphene-based composites, especially, the SiC/graphene composites [14].

The Author declares that there is no conflict of interest.

1. WL Chen, RS Karmakar, YC Liao, YW Lu (2021) Development of a Highly Sensitive Wearable Tactile Sensor on Fabric by Using Conductive Inks Based on Electrical Contact Resistance (ECR) Change Mechanism, Macromolecular Materials and Engineering 306(8).
2. JH He (2008) A new resistance formulation for carbon nanotubes. Journal of Nanomaterials 2008.
3. X Ling-Yi, Y Li, XX Li, JH He (2020) Detection of Cigarette Smoke Using a Fiber Membrane Filmed with Carbon Nanoparticles and a Fractal Current Law. Thermal Science 24(4): 2469-2474.
4. JH He (2005) Resistance in cell membrane and nerve fiber. Neuroscience letters 373(1): 48-50.
5. XX Li, LY Xu, JH He (2020) Nanofiber’s membrane for detecting heavy metal ions. Thermal Science 24(4): 2463-2468.
6. X Yao, JH He (2020) On fabrication of nanoscale non-smooth fibers with high geometric potential and nanoparticle’s non-linear vibration. Thermal Science 24(4): 2491-2497.
7. JH He, QT Ain (2020) New promises and future challenges of fractal calculus: from two-scale Thermodynamics to fractal variational principle. Thermal Science 24(2): 659-681.
8. QT Ain, JH He (2019) On two-scale dimension and its applications. Thermal Science 23(3): 1707-1712.
9. JH He (2018) Fractal calculus and its geometrical explanation. Results in Physics 10: 272-276.
10. JH He (2021) Seeing with a Single Scale is Always Unbelieving: From magic to two- scale fractal. Thermal Science 25(2B): 1-4.
11. YT Zuo, HJ Liu (2020) A Fractal Rheological Model for SiC Paste using a Fractal Derivative. Journal of Applied and Computational Mechanics 6 (SI): 1434-1439.
12. Y Zuo (2021) Effect of SiC particles on viscosity of 3-D print paste: A fractal rheological model and experimental verification. Thermal Science 25(3 Part B): 2405-2409.
13. YT Zuo (2021) A gecko-like fractal receptor of a three-dimensional printing technology: a fractal oscillator. Journal of Mathematical Chemistry 59(3): 735-744.
14. YT Zuo, HJ Liu (2021) Fractal approach to mechanical and electrical properties of graphene/sic composites. Facta Universitatis-Series Mechanical Engineering 19(2): 271-284.
15. JH He (2020) A new proof of the dual optimization problem and its application to the optimal material distribution of SiC/graphene composite. Reports in Mechanical Engineering 1(1): 187-191.
16. JH He, YO El-Dib (2020) Periodic property of the time-fractional Kundu- Mukherjee-Naskar equation. Results in Physics 19(1): 103345.
17. L Lin, SW Yao (2019) Fractal diffusion of silver ions in hollow cylinders with unsmooth inner surface. Journal of Engineered Fibers and Fabrics 14 (1): 155892501989564.
18. X Li, Z Liu, JH He (2020) A fractal two-phase flow model for the fiber motion in a polymer filling process. Fractals-Complex Geometry Patterns and Scaling in Nature and Society 28(5): 2050093.
19. JH He (2019) A simple approach to one-dimensional convection-diffusion equation and its fractional modification for E reaction arising in rotating disk electrodes. Journal of Electroanalytical Chemistry 854: 113565.
20. CH He, C Liu, JH He, AH Shirazi, HM Sedighi (2020) Passive Atmospheric water harvesting utilizing an ancient Chinese ink slab. Facta Universitatis-Series Mechanical Engineering 19 (2): 229-239.
21. JH He, YO El-Dib (2020) Homotopy perturbation method for Fangzhu oscillator. Journal of Mathematical Chemistry 58(10): 2245-2253.
22. CH He, JH He, HM Sedighi, Fangzhu (2020) An ancient Chinese nanotechnology for water collection from air: History, mathematical insight, promises, and challenges. Mathematical Methods in the Applied Sciences.