Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2637-4595
Review Article(ISSN: 2637-4595) 
The Definition Technological Parametres of One Chamber Two Saw Cylinders Gin Volume 1 - Issue 1
Azizov Shuhrat Mamatovich*, Sardorbek Isroilov, Jamoliddin Abdurakhimov and Shokir Turgunov
- Namangan Institute of Engineering and Technology, Russia
Received: January 02, 2018; Published: January 19, 2018
*Corresponding author: Azizov Shuhrat Mamatovich, Namangan Institute of Engineering and Technology, Str. Kasansay7, Namangan 160115, Uzbekistan, Russia
DOI: 10.32474/LTTFD.2018.01.000105
Abstract
In article it is showed the definition technological parameters of one chamber two saw cylinder gin. For maintenance of efficiency of ginning and productivity increase it is necessary to choose correctly diameter of the working chamber, an arrangement corner saw cylinders under the relation of a horizontal axis. These factors are major factors influencing productivity and quality of a fiber at practical and theoretical researches of one chamber two saw cylinder gin.
Keywords: Regression Model; Optimization of Parameter; Angular Position; Saw Cylinder
Introduction
The choice of the necessary technological parameters is the main responsible stage in the design of cotton gin with new working bodies. In the process of fiber separation from the seed, the increase in productivity and the effective elimination of seed damage depend on the selected input parameters. The use of mathematical methods in planning practical experimental work in comparison with other methods of calculation, optimization parameters allows determining the influence of several factors acting together and their interaction among themselves in terms of separation. As a result, based on the few experiments that have been carried out, it is possible to obtain a mathematical model of the object under study; this model will allow obtaining optimal solutions at the time. In optimization, the main issue is this determination of the important factors affecting the process of hair removal of cotton fiber from seed this will serve for efficient fiber separation in the process of ginning [1-3]. The following parameters we chose for optimization:

Using the results of the theoretical study including the literary survey of gins and also taking into account the primary one-factor experiment, the choice of the output parameters affecting the incoming factors was chosen as follows.

Feed rolls 1 feeding the pin drum 2, a bracket and a clamping bar 3, a brush drum 4, a shaft of the brush drum 5, a saw cylinder 6, an upper grate 7, a gin working chamber 8, a lower grate 9, a cement cylinder 10, a screw 11, knife-like mesh surface 12 (Table 1) and (Figure 1).
Table 1: Factor name and numbering.
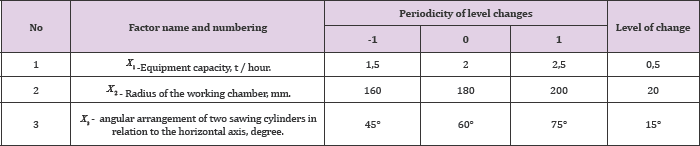
Figure 1: New Gin Machine.
The theoretical studies, it was justified to create a new design for two-cylinder gin. The main working body of the new design is an additional saw cylinder, which allows uniform rotation of the raw roller of productivity. To ensure the efficiency of fiber separation and increase productivity, it's necessary to choose the diameter of the working chamber correctly, the angle of the sawing cylinders in relation to the horizontal axis. These factors are the main factors effecting the productivity and quality of fiber in practical and theoretical studies. The process of ginning associated with many factors is investigated by modern mathematical methods of planning and is calculated by modern computer programs with the help of a computer [4-6]. These methods allow you to get the optimal solution with the least cost. On the basis of the indicators of natural factors, we turn to the coded indicators. The full-factorial test results showed that the investigated process is expressed by the high-level equation. Because of this, to obtain a regression mathematical model of the second degree, this model is considered to be simple and convenient in comparison with other methods, and also in the primary cotton processing enterprises, a non-method method is widely used in technological processes. It was chosen and used in the conducted experiment. The results of the central non composite experimental matrix are given in Table 2.
Table 2: Central non-composite experimental matrix.
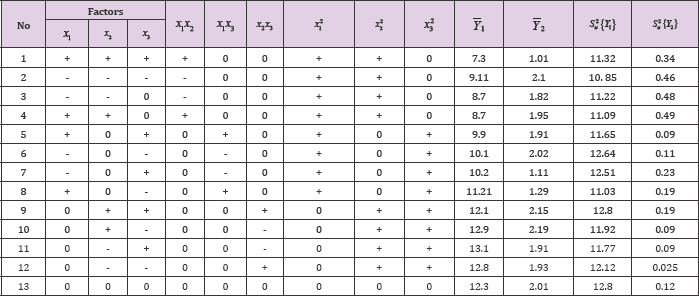
For each experiment it is necessary to use instruments with high accuracy of measurement. In our studies, to change the dimensions of the working chamber, we used already prepared working chambers of different diameters.The fiber performance we determined by the existing method and formula. When using a new working chamber, 100 kg of raw cotton was shipped from the feeder hopper. Each variant of the experiment was conducted five times. In the course of the experiment, the angular arrangement of the saw cylinders with respect to the horizontal axis exerted a great influence on the productivity. The design of the working chamber was made with a high level of measurement. The experiments were conducted according to the principle of randomization. After each experiment (at a certain time), the fiber yield level is determined. After the experiment, the samples were tested according to standard requirements in special laboratories for fiber and mechanical damage to the seeds. Based on the results obtained during the experiment, we use a multifactorial regression mathematical model of the second degree.

I. Calculation of the productivity of the fiber. Define the coefficients of regression:
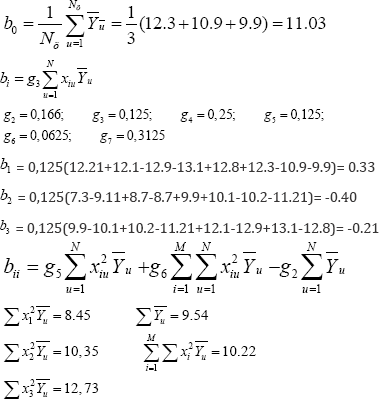

Write the equation according to a certain regression coefficient:
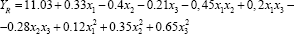
Let.com determine the regression coefficient by acceptability.
To do this, we define the variance of the output parameters
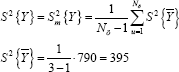
And based on the determination of the regression coefficient, we calculate the variance:
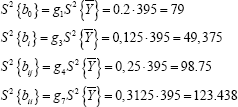
When determining the regression coefficient, we determine the standard deviation:

After this, using the following equation, we determine the indications by the Student's criteria:
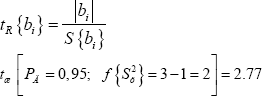
It is known that if the calculated criterion data are lower than those given in the data table, then the coefficient is not important and we derive the data from equation It was found that for the parameters under study, the coefficients of the experiments are not important and necessary:
Let.com re-write the equations with significant coefficients:
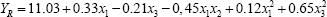
To determine the above regression mathematical model for adequacy and inadequacy, we use the test data of the Fisher criteria.
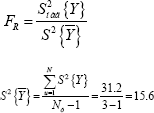
Here,
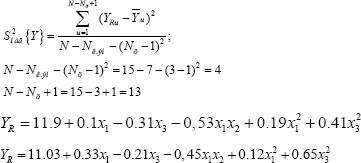
For the results of the output parameters, we use the three factorial two-power regression mathematical model of the equation:
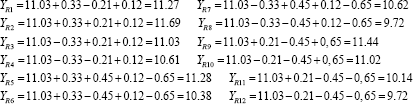
An analysis was made of the data obtained from the three factor mathematical regression model taking into account the necessary regression coefficients by the Student's criterion and also the results of the models tested for Fisher's adequacy.
After In order to simplify the calculations, we create a Table 3:
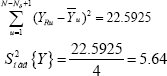
Table 3: Indicators of the Student's test can be taken from the application:
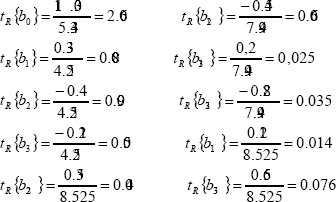
It is known that if the data of the calculation criteria is lower in comparison with the data given in the table, then this coefficient is adequate and this makes the calculations correct.
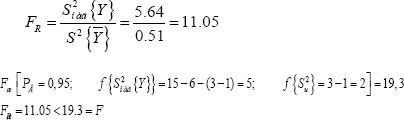
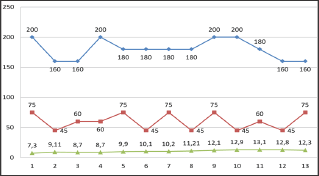
From this it follows that the regression mathematical model obtained fully characterizes the process of investigation (Table 4) and (Figure 2).
Table 4: Regression model

Conclusion
Comparison of the obtained data by the experimental method and the obtained regression mathematical model fully characterizes the process of research with accuracy. Thus, the optimal technological parameters of the single-chamber doublecylinder gin were determined. It can be seen from Figure 2 that when the saw cylinders are positioned at 450-600 degrees relative to the horizontal axis with a working chamber diameter of 180 mm, it makes it possible to increase the productivity by synchronizing the fiber quality. From this it follows that when designing a two-cylinder gin, it is necessary to comply with optimal regime for improving fiber quality and productivity.
Figure 2: Graph of the regression model.
Blue line-diameter of chamber;
Red line-saw cylinders positioned at 450-600 degrees
relative to the horizontal axis;
Green line-capacity of fiber kg/hour.
References
- GI Miroshnechenko (1972) Bases of Designing of Machines of Primary Processing of Cotton Book Theory of Ginning Machine, Moscow, USA.
- SN Nikiforov (1966) Resistance of materials Publishing house "Higher school”, Moscow, USA.
- Mamatovich, A Sh, Axmedhodjaev XT (2015) Theoretical Analysis of Gin Cylinder for Simulating Dual Saw Cylinder Chamber Gin for Increasing Wear proof, Energy Efficient, Saving Resources. Scientific Research 3(3): 91-99.
- Shuhrat Mamatovich Azizov, Xamit Tursunovich Axmedhodjaev (2016) the Optimal Modeling of an Angular Position of Saw Cylinders in SingleChamber Two Cylinders Gin. American Journal of Mechanical and Industrial Engineering 1(3): 103-106.
- Mamatovich, A Sh, Abdusamat K, Arras P (2013) The Mathematical Simulation of Brush Drums in a Dual Saw Cylinder Chamber Gin for the Purpose of Increasing the Quantity of Captured Cotton Fiber from Saw World Journal of Mechanics 3: 58-61.
- Mamamtovich AS (2016) Analysis of the Influence of Geometric Characteristics of the Saw and the Gasket of Saw Gin on the Life of Saw at Different Distances between the Saw. J Textile Sci Eng 6: 256.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...