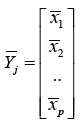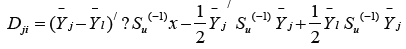Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2638-5910
Review Article(ISSN: 2638-5910) 
A Note on the Application of Discriminant Analysis in Medical Research Volume 2 - Issue 2
KC Bhuyan*
- Department of Statistics, Dhaka, Bangladesh
Received:May 27, 2019 Published: June 06, 2019
Corresponding author:KC Bhuyan, Department of Statistics, Dhaka, Bangladesh
DOI: 10.32474/ADO.2019.02.000132
Introduction
The social aspects of medical research and research in life science deal with data collected from randomly selected investigating units either by direct interview or by doing some controlled experiments. The objective of investigation is to verify the existence of some pre-assumed hypothesis and belief. Whatever be the objective of the research, the study is done using the collected data, where the data are either categorical or numerical or both. There are many advanced statistical methods [1] to handle the data, especially if the data are numerical. Limited number of methods of analysis is there to handle the categorical data. But proper statistical methods are to be applied to study the unknown characteristics in the population. Once the technique of analysis is identified, the analysis can be done using any one of the Statistical Packages available for the analysis. The major source of data in the field of life science and medical science is related to public health and the main aspect of analysis is to suggest ways and means to improve the health status of the public by controlling the diseases which are fatal as well as causes of health hazard in the society. Any type of health hazard is the cause of economic and social problems for the country as well as for the family. Thus, the health planners need the proper analytical findings to formulate the guidelines so that the health hazard is reduced to a great extent. The data are collected from each and every investigating unit.
Some of the data are age, height, weight, level of education, occupation, income, marital status, type of work, food habit, smoking habit, prevalence of obesity, diabetes, hypertension, etc. The prevalence of obesity is the cause of non-communicable diseases like diabetes and hypertension and the sources of these two are occupation, work type, food habit, smoking habit. There may be other sources of diseases. But the sources mentioned here are categorical (qualitative) variable. The quantitative variable income, age, weight, etc. are also the sources of non-communicable diseases [2]. The data mentioned above are the multivariate data. The analytical procedures of these data are different, and the procedures are broadly classified as
a)Dependence Analysis
b)Interdependence Analysis.
One of the techniques of dependence analysis is the Discriminant Analysis. This analysis is used to discriminate the investigated units according to some categorical variable and to identify the most responsible variable(s) for the discrimination. Accordingly, the health planners can suggest the ways and means so that proper action can be taken to control the sources responsible for the health hazard in the society.
Discriminant Analysis
Let xij be the i-th variable observed from j-th category of units [ i = 1, 2, ……..p ; j= 1, 2, …., k], where
Sj = Variance- Covariance matrix of (xi j) , Su = Combined variance- covariance matrix, where
Su = Σ nj Sj / ( n – k ). Here nj = number of observation in j- th category, n = Σ nj.
The k category of units can be discriminated by
a)ML Method of Discrimination
b)Bayes Discriminant Rule and
c)Fisher’s Discriminant Rule.
The ML method of discrimination needs to calculate the following statistic
where j ≠ k.If we consider that k = 3, then there exists linear relationship of the type
D12 + D23 = D13.
In such a situation the value of x will be allocated to a population as per the rule discussed below:
a) If D12>0 and D13>0, allocate x to the population -1
b) If D12<0 and D13>0, allocate x to the population -2
c) If D12<0 and D13<0, allocate x to the population -3.
The discriminant analysis is meaningful if the k mean vectors of variables are heterogeneous. For the analysis a model is considered when there are k = 2 groups, where the model is
D = B0 +B1 x1 + B2 x2 + …………. + Bp xp
Here Bi (i = 1, 2, ….,p) is the discriminant coefficient of the variable xi . The interpretation of these coefficients are closely follows the logic of multiple regression. The value Bi indicates the importance of the variable xi in discriminating between the two groups. For k=3 groups problem, one function is considered to discriminate between first group and combined second and third group. Another function is considered to discriminate between second and third group. The number of discriminant functions are (k – 1) if their k groups. In that case the interpretation of coefficients is made for each function separately. The coefficients are available using Statistical Packages. D is the discriminant score for different values of x when k=2. The correlation coefficient of discriminant score and the variable is used to decide an important variable for discrimination. The highest correlation coefficient indicates the most important variable for discrimination. Different functions may identify different important variables for discrimination.
Some Results of Discriminant Analysis
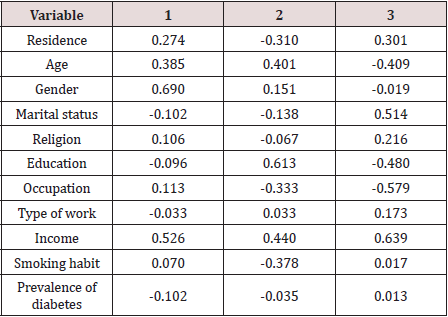
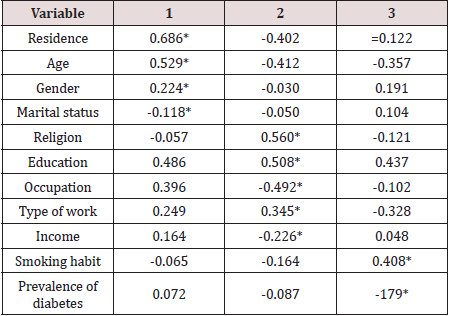
The following Discriminant Analysis was done [3] to discriminate 900 randomly selected adults of Bangladesh classified by levels of obesity. It was observed that levels of obesity were varied differently with the variation of different social factors. Thus, there were in search of identification of most important variables to discriminate the respondents according to various of levels of obesity. This was done by discriminant analysis. The analysis helps to identify the important variables for which the groups of respondents were significantly different [4]. The variables which were included in the analysis were sufficient to discriminate the different groups of respondents according to their level of obesity as Box’s M = 287.926 and the corresponding F= 1.403 with p –value = 0.000. The analysis provided 3 discriminant functions for 4 groups of respondents. The first function was significant as values of Wilk’s ∧ for first, second and third functions were 0.918, 0.973 and 0.994, respectively and the corresponding x2 values were 75.920( p-value=0.0000, 24.493 ( p-value=0.222) and 5.065 (p-value=0.829). The standardized canonical discriminant function coefficients were presented in Table 1. From the discriminant analysis the correlation coefficients of variables and the discriminant functions scores were calculated. These coefficients were shown in Table 2. The analysis indicated that the respondents of different levels of obesity were significantly different according to socio-demographic variables. The important variable for discrimination was residence followed by age. The other important variables were gender and marital status.
Table 2: Pooled within group correlations between discriminating variables and standardized discriminant function.
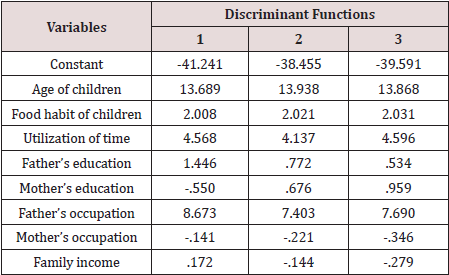
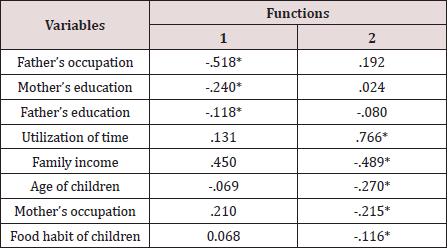
As a second example of discriminant analysis, 662 children and adolescents of some randomly selected affluent families were classified by their level of obesity [5]. There were 4 groups of respondents and for these 4 groups the variables age of the children, food habit of children, utilization of time by the children, father’s education, mother’s education, father’s occupation, mother’s occupation and family income were different and most of them were associated with the level of obesity. Therefore, these variables were included to discriminate the children. For 4 groups of children 3 Fisher’s linear discriminant functions were available. The coefficients of these functions for different variables were shown in Table 3. First function explained 92.7% variation of the children’s level of obesity and most important variable to explain this variation is father’s occupation followed by mother’s education and father’s education. This phenomenon was observed from pooled within groups correlations between discriminating variables and standardized canonical discriminant functions. The results of this pooled within groups correlations were given in Table 4. The most important variables identified by functions were shown by given asterix. Since first functions explained 92.7% variation in level of obesity and this function was statistically significant [ Wilk’s Lamda=0.834, Chi-square =97.811, p-value=0.000], the pooled within groups correlations were shown for this first function. Some variables were also found important by second function to discriminate children by level of obesity. However, the 2nd and 3rd functions were not statistically significant and the pooled within groups correlations of variables and 3rd function were not shown.
As a third example, let us present the results of discriminant analysis when discrimination was done according to the prevalence of non-communicable diseases [NCDs]. A group of adults of Bangladesh was investigated [2] to identify the responsible variable for the prevalence of NCDs. The data were recorded from randomly selected 785 adult people of Bangladesh. Among them, 49.4 percent were affected by at least one of the NCDs. The two groups of respondents were discriminated to identify the factors responsible for discrimination. The analysis indicated that the variables age, followed by marital status and weight were the most important variables in discriminating the two groups of respondents. The analytical results were presented in Table 5. As a fourth example, let us discuss the discrimination of students of public and private universities in respect of some social characters. The number of investigated students were 893 from private universities and 119 from public universities [6].
Table 5: Coefficient of discriminant function and pooled within groups correlation between variables and discriminant function score.
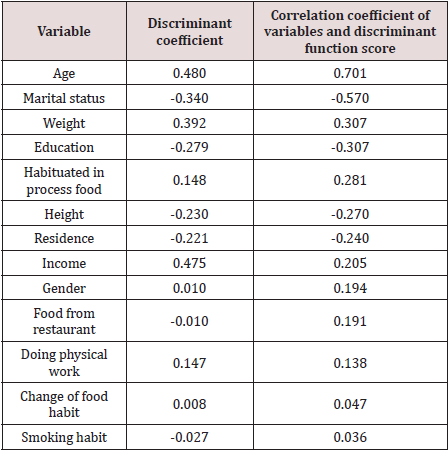
As there were two groups of students, viz. students of public university and students of private university, one discriminant function was derived. The function was
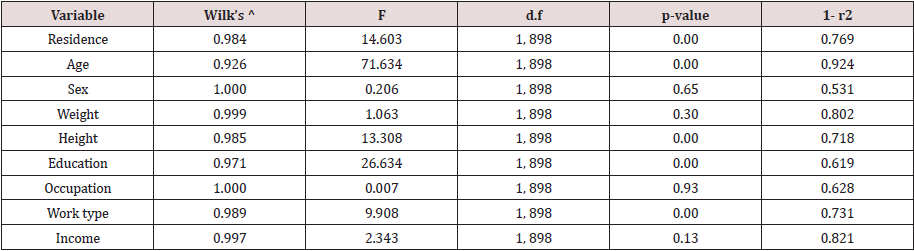
This function was significant as Wilks Lambda is 0.773 [χ2= 258.758, p=0.000, Bartlett (1947)] and it indicated that the students of private and public universities were significantly different in respect of some of the socioeconomic characteristics. The important socioeconomic characteristics were identified by the canonical correlation coefficients of the variables and the discriminant score. The correlation coefficients are shown in Table 6 in descending order of magnitude. It is seen that father’s education is very important social factor to discriminate between student of private and public universities followed by mother’s education, residential origin and age of students. As a fifth example, let us discuss the discrimination of 900 randomly selected adults of Bangladesh [7] in respect of the prevalence of diabetes. There were two groups of respondents, one group of 635 diabetic patients and another group of 235 normal respondents. In doing the discriminant analysis, there was an attempt to decide the inclusion of variables in the discriminant analysis. For this the value 1- r2 was calculated and was shown in Table 7. Here r is the multiple correlation coefficient when one variable was considered as dependent variable and others as independent variable. None of these calculated values was low and hence all the nine variables were included in the analysis.
Table 6: Correlation coefficient between variables and discriminant score in descending order of magnitude.
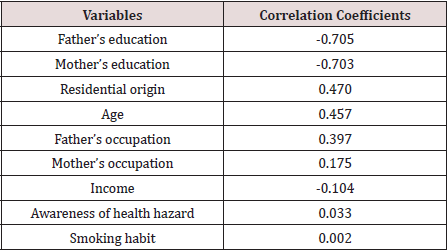
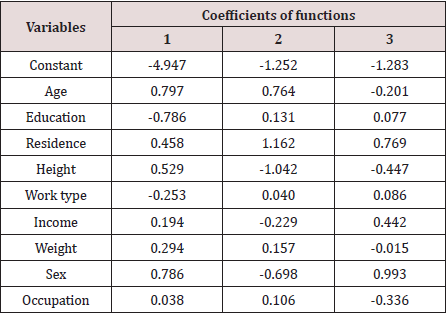
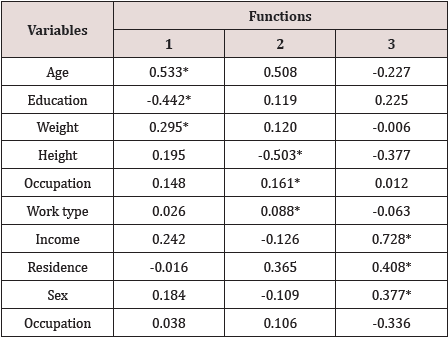
The discriminant coefficients were shown in Table 8 below. The results indicated that the variable residence had the highest discriminating power followed by work type, income and age. The importance of the variables was also observed from the study of the correlation coefficients of the variables with discriminant score. The correlation coefficients in descending order were shown below in Table 9. The function was found highly significant by Bartlett’s test (p<0.001). The test indicates that diabetic and non-diabetic respondents were significantly different. The important variable for discrimination was age followed by education and residence. This result was observed from the study of correlation coefficient of the variables and discriminant score. The same of respondents were also discriminated by the type of disease. The total diabetic patients were classified in to four classes, viz. patients of type I, type II, type III diabetes and another group of 269 patients who were ignorant about their type of diabetes. In the first three groups the number of patients were 136, 215 and 19 respectively.
Thus, the patients were classified into 4 groups and identified the groups by 1, 2, 3 and 4 respectively. The multivariate analysis of variance showed that the mean vectors of four groups of patients by type were significantly different (Wilk’s ^ = 0.891, F= 2.715, p ≤ 0.01The discriminant analysis also showed that the 3 discriminant functions were significantly different ( p ≤ 0.01). The results were shown in Table 10. The pooled within- groups correlations between discriminating variables and the standardized canonical discriminant functions were shown in Table 11. The first function discriminated well among groups of patients and the variables age and education were important to discriminate among patients of different types of diabetes. The second function discriminated well and the important variables for discrimination were occupation and work type. The third function discriminated well among different groups of patients of different types and the variables income, residence and sex were very important to discriminate well.
Introduction
- Bhuyan KC (2018) A note on the application of advanced statistical methods in medical Research. Biomed J Sci & Tech Res 11(3): 1-4.
- Bhuyan KC, Mortuza A Md, Fardus J (2018) Discriminating patients suffering from non-communicable diseases: A case study among Bangladeshi adults. Biomed J Sci & Tech Res 10(1): 7571-7577.
- Bhuyan KC, Fardus J (2019) Discriminating Bangladeshi adults by level of obesity. LOJ Med Sci 3(1): 184-190.
- Bhuyan KC (2004) Multivariate Analysis and its Application, New Central Book Agency (P) Ltd, India.
- Urmi AF, Bhuyan KC (2019) Discriminating Bangladeshi children and adolescents of affluent families by level of obesity. AJSE.
- Bhuyan KC, Urmi AF, Fardus J (2017) Discriminating students of public and private universities in respect of some social characters. Jour Stats Studies 34: 13-23.
- Fardus J, Bhuyan KC (2016) Discriminating diabetic patients of some urban and rural areas of Bangladesh: A Discriminant Analysis Approach. Euro Biomed Jour for Young Doctors 11(19): 134-140.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...