Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6744
Review articleOpen Access
Three New(?) Properties of an Ellipse and an Ellipsoid of Revolution (Computer Analysis) Volume 2 - Issue 4
A Kornyushkin*
- Moscow Institute of General and Applied Physics, Russia
Received: February 20, 2022; Published: March 02, 2023
*Corresponding author:A Kornyushkin, Moscow Institute of General and Applied Physics, Russia
DOI: 10.32474/CTCSA.2023.02.000143
Abstract
Found (on a computer, without proof) two Invariants and one correspondence for the motion of a beam in a mirror ellipse and an ellipsoid of revolution.
New(?) Ellipse Invariants
First invariant
basic circle (R) of the ellipse and sequences of reflections v.
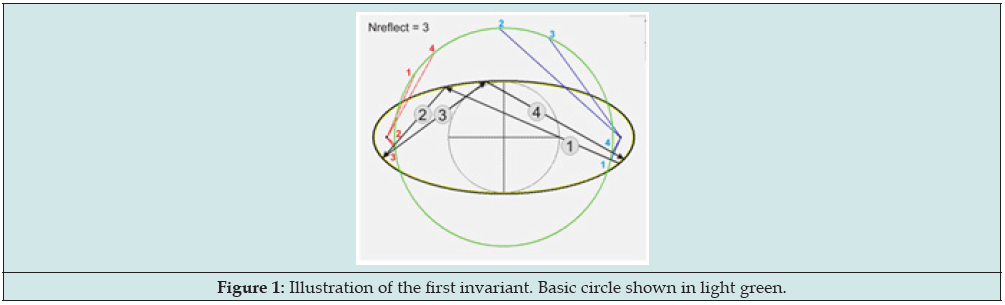
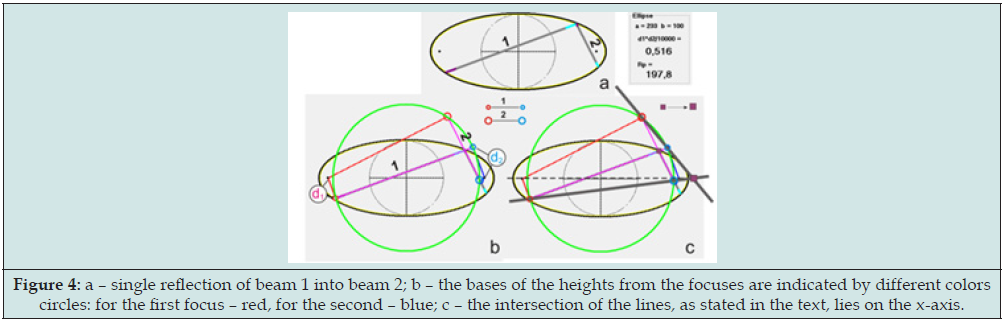
Let’s imagine a beam of light in a two-dimensional plane, which is inside a mirror ellipse with semi-axes a and b; a>b. A beam of light is successively reflected from it. Let’s call reflected rays (vectors): v1 -> v2 -> v3… ; lines on which they lie: p1, p2, p3... . Then the bases of the heights drawn to these lines from the focuses of the ellipse lie on a circle of radius R centered at the center of the ellipse. We call this circle the basic circle for the given ellipse and the given sequence v Figure 1.
Second invariant
For any line which the ray follows, the valid formula is.
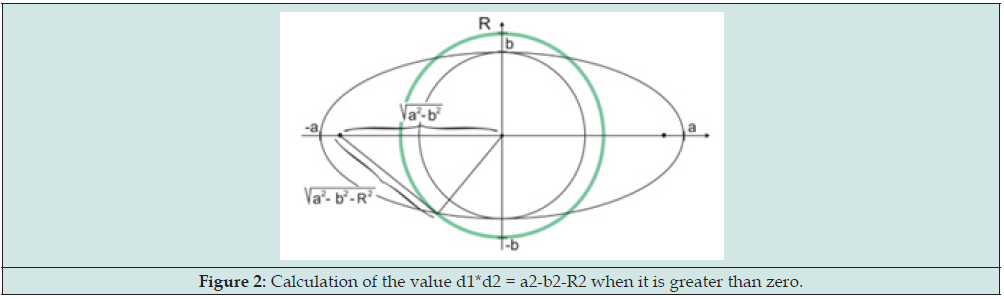
d1*d2=|a2-b2-R2| [1]
where d1 and d2 are the distance from the focus to this line.
It is surprising that this fact is absent anywhere! Everywhere [1,2] is only the fact that “product of distances from focuses to tangent to ellipse is a constant”, although this fact is the passage to the limit of our formula. The product d1*d2 can be either less than zero or greater Figure 2.
The third property.
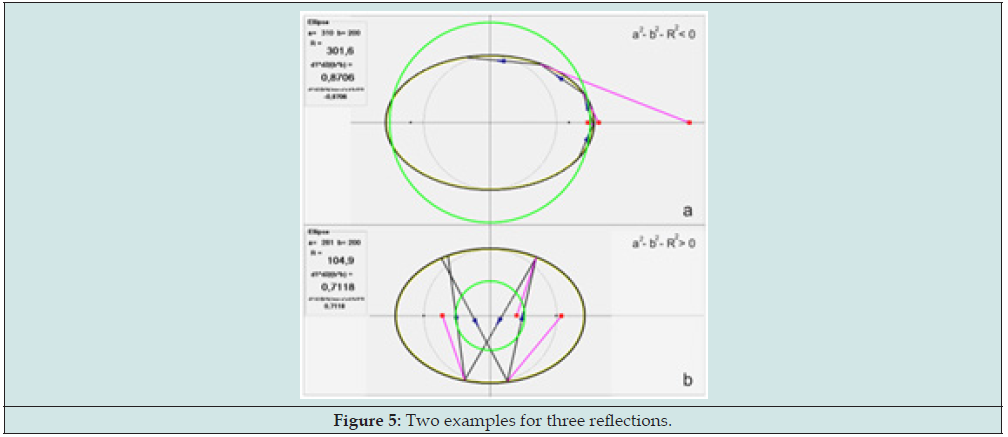
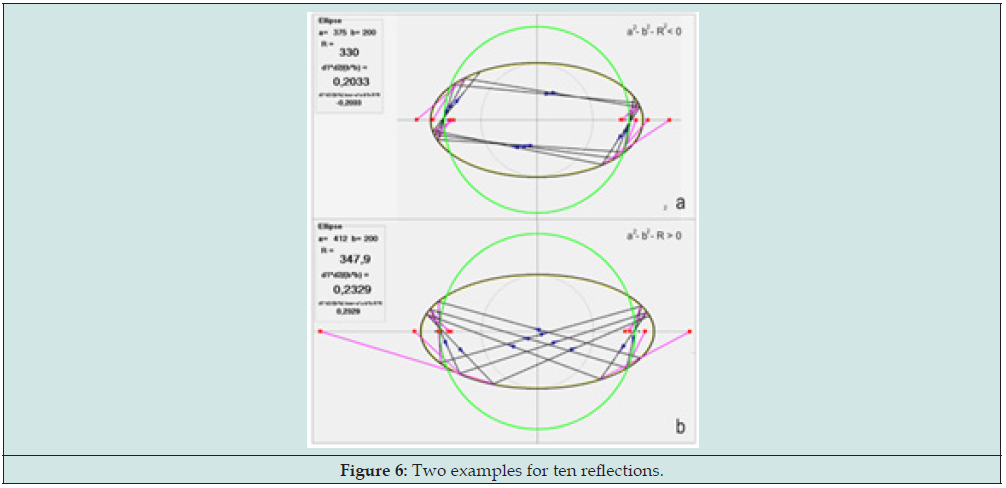
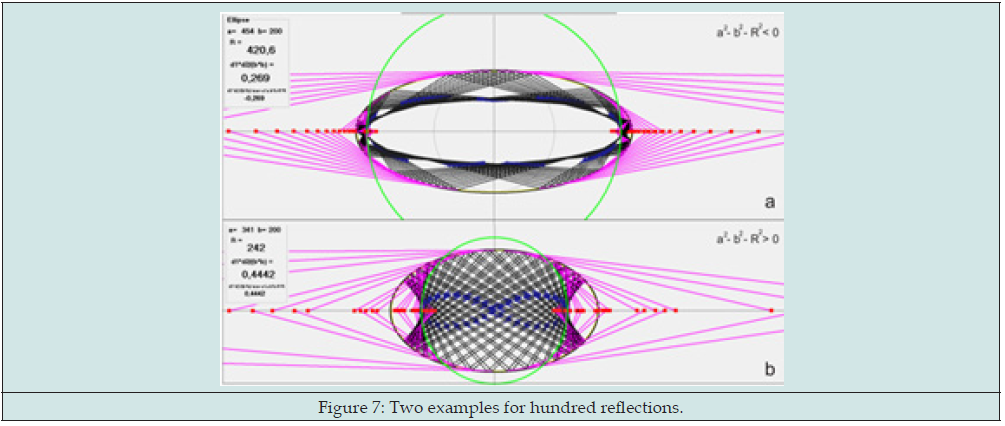
Let’s “color” the focuses of an ellipse with the different colors: the first in red; the second in blue. Then it follows from the first invariant that our vectors v1, v2… in the ellipse can be put in correspondence with a sequence of chords on the basic circle, one end of which will be red, the other blue Figure 3. Then if you connect the end of the blue n-1-th chord with the red end of the n-th chord, and the red end of the n-th chord with the blue end of the n-1 chord, then the intersection of this lines will lie on the X axis of the ellipse. That is, each point of reflection of the rays with ellipse corresponds with a point lying on the X axis. Figure 4. Three figures, for three different reflections are presented: Figures 3-5 reflections; Figures 6-10 reflections and Figure 7: 100 reflections. Each figure shows two examples with different signatures for the quantity a2-b2-R2. The value of the semi- axes of the ellipse in each case are taken differently.
Figure 3: a – the product d1*d2=a2-b2-R2 is greater than zero; b - the product is less than zero for an ellipse.
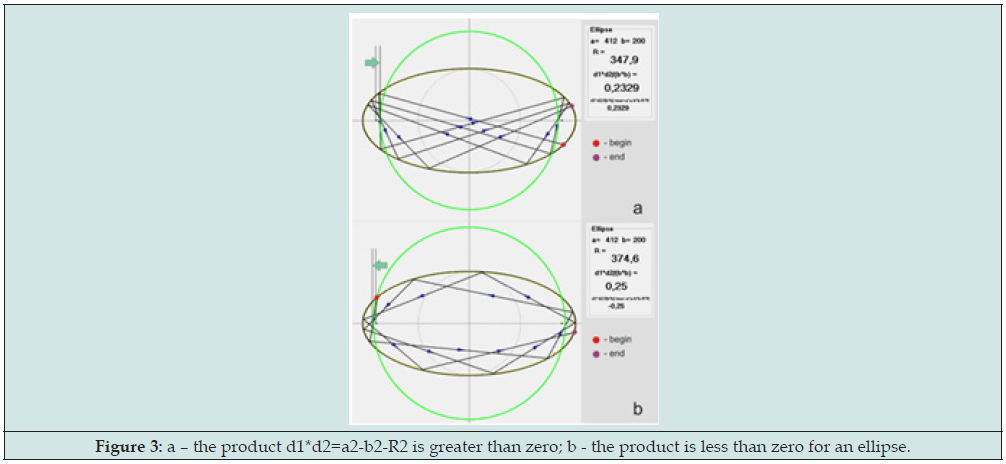
Figure 4: a – single reflection of beam 1 into beam 2; b – the bases of the heights from the focuses are indicated by different colors circles: for the first focus – red, for the second – blue; c – the intersection of the lines, as stated in the text, lies on the x-axis.
Invariants for ellipsoid of revolution in ndimensional space
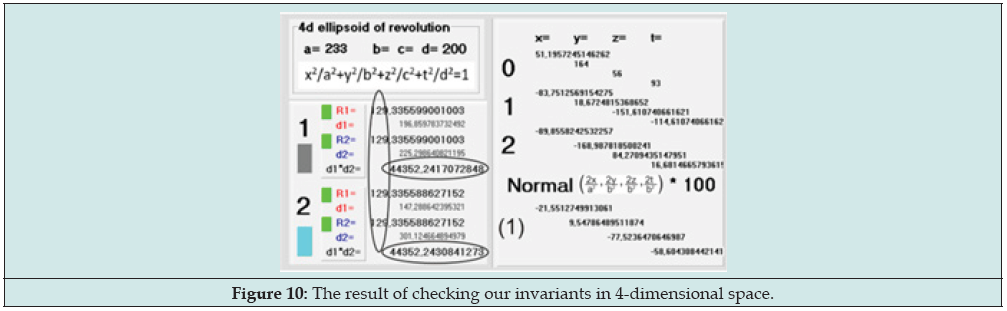
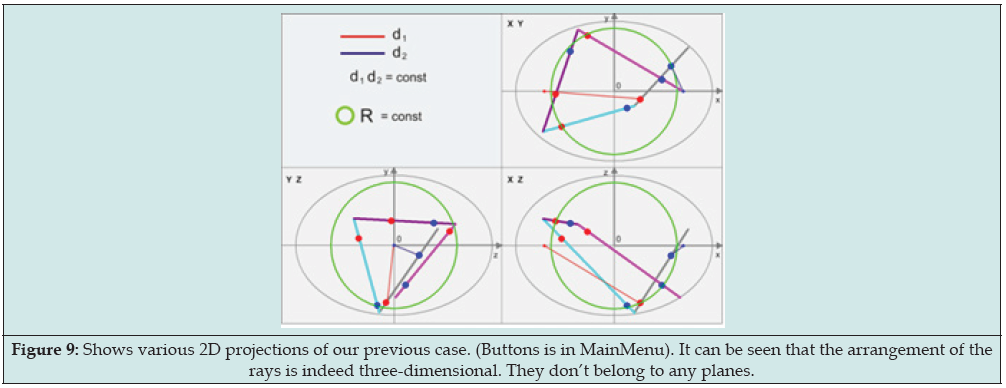
It is interesting that the first two invariants (not formula [1]!) is carry out over almost unchanged to any dimension Figure 7. Namely: the basic circle turns out into a basic sphere in n dimension, and the perpendicular from focuses to the lines turns out into perpendiculars to the lines in n- dimensional space [3]. There is a free program on the Internet at [4] that confirms this. (In it, to switch to 3d, select 3d -> Have 3d in the Main Menu and press the “New” button on the panel that appears) Figure 8. Ellipsoid parameters (a and b=c) can be changed (in Main Menu). By pressing the left mouse button and dragging on canvas, you can change the tilt of the z-axis Figure 9. The program has buttons to check our invariants in 4d. Figure 10 shows the calculation result for one reflection. It can be seen, as in 3D, the complete preservation of the results. It is obvious that these invariants are preserved in any dimensions.
Figure 8: a - The program produces three reflections of a random beam from a mirror (from the inside) ellipsoid of revolution. The ray in the image, after each reflection, is painted with a different color. The “gray” beam of light turns out into a “light blue”; then to “blue-red” (violet); then to “pink” (fuchsia). One focus (left) is colored red, the other colored blue. The bases of the heights are drawn with the same colors. All these bases are at equal distances from the center of the ellipsoid (vertical oval on Figure 8b). The products of distances from two focuses also coincide (horizontal ovals on Figure 8b). But at the same time, formula [1] no longer works!
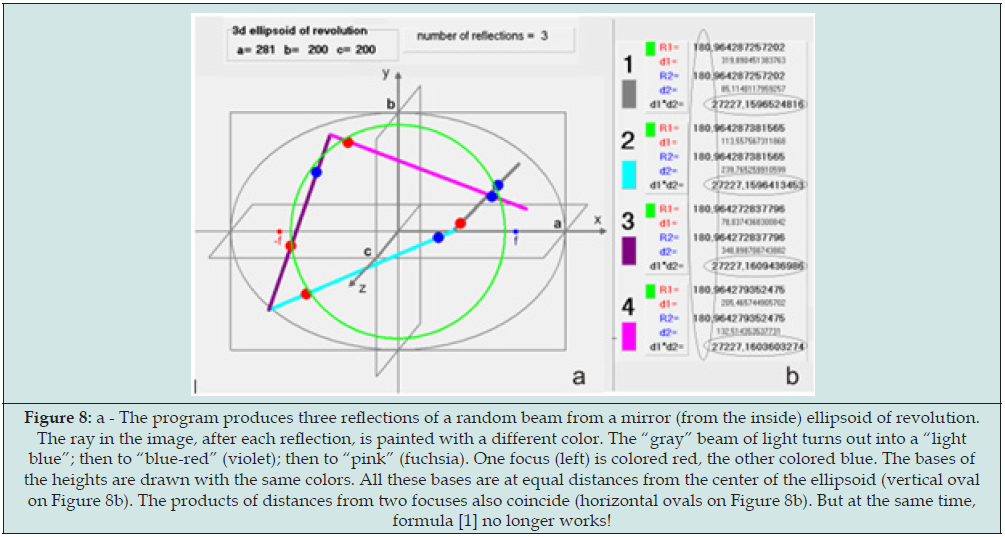
Figure 9: Shows various 2D projections of our previous case. (Buttons is in MainMenu). It can be seen that the arrangement of the rays is indeed three-dimensional. They don’t belong to any planes.
Conclusion
The web resource [4] contains the source code and formulas for calculation. They are very simple and transparent. Proposing a rigorous proof of these facts is a difficult and interesting task.
References
- Granino A Korn, Teresa M Korn (1961) Mathematical handbook for scientists and engineers; Definitions, theorems and formulas for reference and review.
- Aleksandrov P S (1968) Lectures on analytic geometry. Nauka, Moscow, Russia.
- http://math.phys.msu.ru/data/24/Zadachi_angeom.pdf
- https://disk.yandex.ru/d/AzqXOACqAZBsCA

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...