Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2643-6744
Research Article(ISSN: 2643-6744) 
Numerical Solution of Boundary Layer Flow of Viscous Fluid Via Successive Linearization Method Volume 1 - Issue 2
Faisal Salah2* and Abdelmgid OM Sidahmed1
- 1 Department of Mathematics, Saudi Arabia
- 2 Department of Mathematics, Sudan
Received:November 19, 2018; Published:December 04, 2018
*Corresponding author: Faisal Salah, Department of Mathematics, Saudi Arabia
DOI: 10.32474/CTCSA.2018.01.000108
Abstract
The aim of this work is to obtain the numerical solutions for the boundary layer flow of heat transfer of incompressible viscous fluid. The governing partial differential equations are converted into ordinary differential equation by using a similarity transformation. The nonlinear equation governing the flow problem is modeled and then solved numerically by means of a successive linearization method (SLM). The numerical results are derived in tables for comparisons. The important result of this comparison is to show the high precision of the SLM in solving system of nonlinear differential equations. Graphical outcomes of various parameters such as Prandtl number (Pr) and Eckert number (Ec) on the flow, field are discussed and analyzed. Besides this the present results have been tested and compared with the available published results in a limiting manner and an excellent agreement is found.
Keywords: Viscous fluid; Successive linearization; Boundary layer
Introduction
In the recent years, a great deal of interest has been gained to fluids applications. Some fluids not easy to expressed by particular constitutive relationship between shear rates and stress and which is totally different than the viscous fluids [1,2]. These fluids including many home items namely, toiletries, paints, cosmetics certain oils, shampoo, jams, soups etc. have different features and are denoted by non-Newtonian fluids. In general, the categorization of non-Newtonian fluid models is given under three class which are named the integral, differential, and rate types [3-6]. In the present study, the main interest is to discuss the heat transfer flow of hydrodynamic viscous fluid over a flat plate in a uniform stream of fluid with dissipation effect. The most phenomena in the field of engineering and science that occur is nonlinear. With this nonlinearity the equations become more difficult to handle and solve. Some of these nonlinear equations can be solved by using approximate analytical methods such as Homotopy analysis method (HAM) proposed by liao S [7,8], Homotopy Perturbation method (HPM) it was found by Ji-Huan [9] and Adomain decomposition method (ADM) Q Esmaili et al. [10], Makinde OD et al. [11] and Makinde OD [12].
However, some of these equations are solved via traditional numerical techniques such as finite difference method,shooting method and Keller box method, Runge-Kutta. Recently some studies have presented a new method called Successive Linearization Method (SLM). This method has been applied successfully in many nonlinear problems in sciences and engineering, such as the MHD flows of non- Newtonian fluids and heat transfer over a stretching sheet [13], viscoelastic squeezing flow between two parallel plates [14], two dimensional laminar flow between two moving porous walls [15] and convective heat transfer for boundary layer with pressure gradient [16,17]. Therefore, the effectiveness, validity, accuracy and flexibility of the SLM are verified among of all these successful applications. Presently a new investigation on the heat transfer flow of hydrodynamic viscous fluid over a flat plate in a uniform stream of fluid with dissipation effect is discussed. The numerical solution to the resulting nonlinear problem is computed by using the SLM approach. The embedded flow parameters are discussed and illustrated graphically.
Mathematical formulation of the problem
The governing equations are
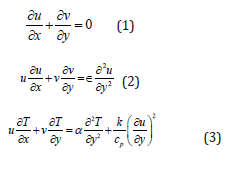
where (u,v ) are the components of velocity in (x , y) directions,
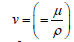 the kinematic viscosity T is temperature of fluid,
the kinematic viscosity T is temperature of fluid,
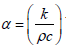 the thermal diffusivity
the thermal diffusivity
k the fluid thermal conductivity, ρc the fluid capacity heat and cp the specific heat. The relevant boundary conditions are defined as
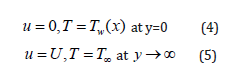
Where , Tw T∞ are constants. Introducing the following dimensionless variables
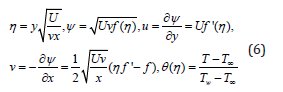
Utilizing equation (6), equation (1) is satisfied automatically and equations (2) and (3) characterize to the following problems statement
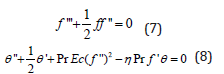
The related boundary conditions
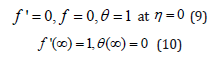
Solution of the problem
Here successive linearization method (SLM) [14-16] is implemented to obtain the numerical solutions for nonlinear system (8) and (10) corresponding to the boundary condition Eq. (11) – (13) (Table 1). The convergence for numerical values of f "(0) and −θ '(0) for different order of approximation when Ec = 0.01, Pr =1 and n =1.00 (Table 1).
Table 1: The convergence for numerical values of f "(0) and −θ '(0) for different order of approximation when Ec=0.01, Pr 1 and 1.00 Ec n=1.00.
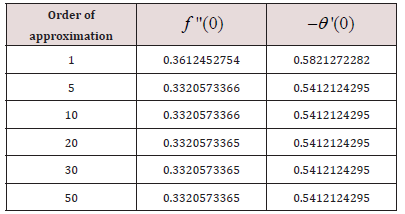
The numerical values of f (η ) and f '(η )when, n =1, Pr =1 for Ec= 0.01. (Table 2).
Table 2: The numerical values of f (η ) and f '(η ) when, n =1, Pr =1 for Ec = 0.01.
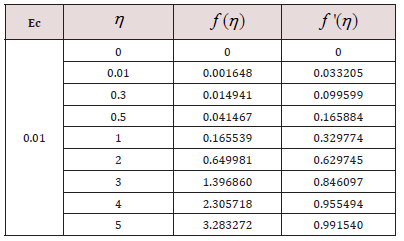
The numerical values of θ (η ) and −θ '(η )when, n =1, Pr =1 for Ec =0.01 (Table 3).
Table 3: The numerical values of θ (η ) and −θ '(η ) when, n =1, Pr =1 for Ec =0.01.
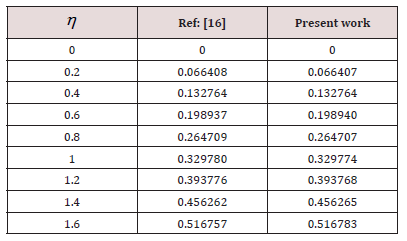
Comparison of numerical values of f (η ) with Ref: [16] when, n= Ec = 0, Pr =1 (Table 4).
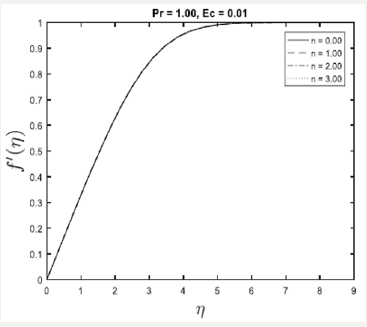
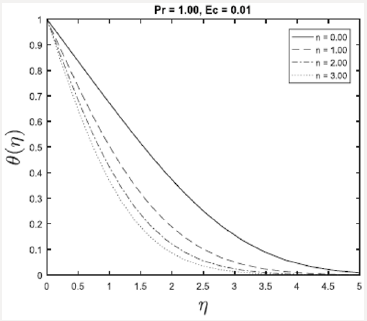
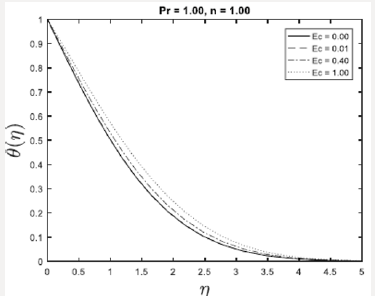
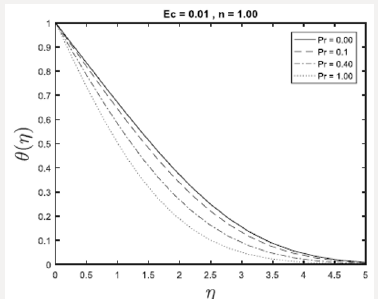
This section concerns with the graphical illustrations obtained by using successive linearization method for velocity, temperature profiles. These profiles show the variations of embedded flow parameters in the solution expressions for heat transfer analysis for an incompressible viscous fluid. The physical interpretation of the problem has been discussed in Figures 1 – 4. These figures are plotted in order to illustrate such variations. Here the graphs have been determined for the heat transfer flow of steady Newtonian fluid. Figures 1 & 2 shows the effects of the parameter on the velocity profile for f '(η ) and θ (η ) when Ec, Pr are fixed. It is worth noticing that by increasing the parameter η reveals that buoyancy because of augments of gravity which boosts on the velocity. Figure 3 is sketched for the variation of Prandtl number Pr on θ (η ) . It is noted that for lager Pr ,the thermal field is lower and then this reduce the temperature. In fact law Prandtl number Pr assist fluid with higher thermal conductivity and this create thicker thermal boundary layer than that for lager Pr. Finally, Figure 4 shows the effect of Ec on velocity and temperature profiles over the plate, and we note that by increasing in Ec parameter is seen that the effect is very big for the temperature.
Conclusion
In this research, the problem of heat transfer of an incompressible viscous fluid over flat pate is solved numerically. The numerical solutions are well established by SLM. The influence of various parameters is shown through different graphs. The present results have been tested and compared with the available published results in [16], in a limiting situation shown in tables v and an excellent agreement is found [17].
References
- R Ellahi, T Hayat, T Javed, S Asghar (2008) On the analytic solution of nonlinear flow problem involving Oldroyd 8-constant fluid. Mathematical and Computer Modelling 48(7-8): 1191-1200.
- T Hayat, Masood Khan, and M Ayub (2004) Couette and Poiseuille flows of an Oldroyd 6-constant fluid with magnetic field. Journal of mathematical analysis and applications 298(1): 225-244.
- C Fetecau, Sharat C Prasad, KR Rajagopal (2007) A note on the flow induced by a constantly accelerating plate in an Oldroyd-B fluid. Applied mathematical modelling 31(4): 647-654.
- F Salah, Z Abdul Aziz, C Ching, D Ling (2011) New exact solutions for MHD transient rotating flow of a second-grade fluid in a porous medium. Journal of Applied Mathematics.
- T Hayat, C Fetecau, M Sajid (2008) Analytic solution for MHD transient rotating flow of a second-grade fluid in a porous space. Nonlinear Analysis: Real World Applications 9(4): 1619-1627.
- R Cortell (2006) A note on flow and heat transfer of a viscoelastic fluid over a stretching sheet. International Journal of Non-Linear Mechanics 41(1): 78-85.
- SJ Liao (1992) The proposed homotopy analysis technique for the solution of nonlinear problems. Diss Ph D Thesis, Shanghai Jiao Tong University
- SJ Liao (2004) On the homotopy analysis method for nonlinear problems. Applied Mathematics and Computation 147(2): 499-513.
- JH He (1999) Homotopy perturbation technique. Computer methods in applied mechanics and engineering 178(3-4): 257-262.
- Q Esmaili, A Ramiar, E Alizadeh, DD Ganji (2008) An approximation of the analytical solution of the Jeffery-Hamel flow by decomposition method. Physics Letters A 372(19): 3434-3439.
- OD Makinde, PY Mhone (2006) Hermite-Padé approximation approach to MHD Jeffery-Hamel flows. Applied Mathematics and Computation 181(2): 966-972.
- OD Makinde (2008) Effect of arbitrary magnetic Reynolds number on MHD flows in convergent-divergent channels. International Journal of Numerical Methods for Heat & Fluid Flow 18(6): 697-707.
- S Shateyi, SS Motsa (2010) Variable viscosity on magnetohydrodynamic fluid flow and heat transfer over an unsteady stretching surface with Hall effect. Boundary Value Problems 1: 257568.
- Z Makukula, SS Motsa, P Sibanda (2010) On a new solution for the viscoelastic squeezing flow between two parallel plates. Journal of Advanced Research in Applied Mathematics 2(4): 31-38.
- ZG Makukula, P Sibanda, SS Motsa (2010) A novel numerical technique for two-dimensional laminar flow between two moving porous walls. Mathematical problems in Engineering pp. 15.
- MAM Ahmed, ME Mohammed, AA Khidir (2015) On linearization method to MHD boundary layer convective heat transfer with low pressure gradient. Propulsion and Power Research 4(2): 105-113.
- MS Abel, JV Tawade, MM Nandeppanavar (2012) MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 47(2): 385-393.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...