Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2637-4609
Review Article(ISSN: 2637-4609) 
Optimization of Chitosan+Activated Carbon Nanocomposite. DFT Study Volume 3 - Issue 5
David Hernández Benitez and Juan Horacio Pacheco Sánchez
- Division of Postgraduate Studies and Research of the Technological Institute of Toluca, Mexico
Received: October 01, 2018; Published: October 09, 2018
*Corresponding author:Juan Horacio Pacheco Sánchez, Division of Postgraduate Studies and Research of the Technological Institute of Toluca, Av. Tecnológico s/n, Agrícola Bellavista, 52149 México
DOI: 10.32474/AOICS.2018.03.000175
Abstract
First, the minimum energy (geometry optimization DFT-DMol3) is obtained among C48 optimized ring carbon-system, and one non-optimized chitosan copolymer unit. Second, C24 and C9 optimized rings, each one interacting with an optimized chitosan copolymer unit (Ch). With the aim to investigate structural properties, the first case is optimized by applying smearing; and the second without smearing. Two parallel hypothetical carbon chains of 12 carbon atoms, symmetrically arranged are optimized in C24 carbyne ring; and one hypothetical 5 carbon-chain parallel to another 4 carbon-chain end optimized in a cumulene C9-ring. These carbon-ring structures here defined as activated carbons (AC), correspond to big pore size diameter obtained without chemical agent acting on them. Single point calculations are to build potential energy surfaces with GGA-PW91 functional to deal with exchange correlation energies for unrestricted spin, all-electron with dnd basis set. Only in the first case, orbital occupation is optimized with diverse smearing values. To determine structure stability, the minimum energy criterion is applied on AC+Ch nanocomposite. To generate fractional occupation, virtual orbitals are formed in this occupation space, whether homo-lumo gap is small and there is certain density near Fermi level. This fractional occupation pattern depends on the temperature. It must be noticed that when AC and Ch are solids, there is no adsorption; however, by applying smearing it was possible to find potential energy surfaces with a high equilibrium energy indicating glass phase transition in Chitosan due to the chemisorption given at the minimum of energy. AC+Ch molecular complex nanocomposite is expected to be applied not only in medicine but also in high technology.
Introduction
With the aim to figure out a molecular complex formed through the interaction between a system of 48 carbons arranged in planar way and a copolymer unit of chitosan, potential energy surfaces were built [1,2] using single point step by step calculations. The problem is studied considering that a molecular complex is obtained by changing smearing value according to the energy value convergence. Considering that electrons occupy orbitals with the lowest energies and with an integral occupation number in calculations of density functionals, a smearing change indicates a fractional occupation in virtual orbitals within this space of occupation. The smearing calculations correspond to the explicit inclusion of the fractional occupation numbers of the DFT calculations, requiring an additional term to achieve a functional energy from variation theory [35]. The contribution of this term to the density functional force exactly cancels the correction term as a function of the change in the occupation number. For occupation numbers satisfying a Fermi distribution, the variation total-energy functional is identical in form to the grand potential [3-6]. From the grand canonical distribution or Gibbs distribution, the normalized probability distribution of finding the system in a state with n particles and energy 𝐸𝑛𝑟 [7], the Z grand partition function of the system, and the number of particles remains according to the Fermi energy ℰf =μ(T,V,n). When T = 0 the fermion gas is in the state of minimum energy in which the particles occupy the n states of 𝜓𝑖 of lower energy, since the exclusion principle of Pauli does not allow more than one particle in each state. Therefore, the Fermi function 𝑓(ℰ) gives the probability that certain states of available electron energy are occupied at a given temperature.
Other options for the shape of the occupancy numbers result from the different associated functional with finite temperature to DFT but without physical meaning, such as the temperature or the entropy associated with this term [3]. These terms, although numerically small must be included in the practical calculations that allow numbers of fractional occupation [3,8]. To consider the scope of smearing, it is known that electrons occupy orbitals with the lowest energies, and occupancy numbers are integers; nonetheless, there is a need for a fractional occupation in virtual orbitals within this space of occupation. We apply this when the HOMO-LUMO gap is small and there is especially a significant density near of Fermi level [9], thus in order to obtain the fractional occupation a kT term is implemented. This fractional occupation pattern depends on the temperature. The systems C48 carbinoid, C24 carbyne-ring, and C9 cumulene-ring (almost-planar) are arrangements obtained through DFT geometry optimization of two hypothetical parallel zigzag linear carbon chains. We consider these systems as carbon physically activated, due to the pore size diameter, and since no activating chemical agent has been applied. Carbyne is known as linear carbons alternating single and triple bonds (-C≡C-) n or with double bonds (=C=C=)n (cumulene) [10]. Polyyne is known as a allotrope carbon having H(-C≡C-) nH chemical structure repeating chain, with alternating single and triple bonds [11] and hydrogen at every extremity, corresponding to hydrogenated linear carbon chain as any member of the polyyne family HC2nH [12] with sp hybridization atoms. It is known that polyyne, carbyne and carbinoid have been actually synthesized as documented by Cataldo [13]. Bond length alternation (BLA) of carbyne pattern is retained in the rings having an even number of atoms [10]. Additional care must be taken with carbyne rings since the Jahn-Teller distortion (the counterpart of Peierls instability in non-linear molecules) is different in the C4N and C4N+2 families of rings [14-16]. There is a great variety of applications of activated carbon as an adsorbent material, and it has been used in areas related to the energy, and the environment, generating materials with a high-energy storage capacity [17].
Chitin is, after cellulose, the most abundant biopolymer in
nature. When the degree of deacetylation of chitin reaches about
50% (depending on the origin of the polymer), it becomes soluble
in aqueous acidic media and is called chitosan [18]. Chitosan is
applied to remediation of heavy metals in drinking water and other
contaminants by adsorption. The affinity of chitosan with heavy
metals makes the bisorption process stable and advantageous, being
only by the alginates present in brown algae matched [19]. The glass
transition temperature of chitosan is 203°C (476.15 K) according
to Sakurai et al. [20], 225°C (498.15 K) according to Kadokawa
[21], and 280°C (553.15 K) according to Cardona-Trujillo [22].
One can differentiate specific reactions involving the -NH2 group at
nonspecific reactions of -OH groups. This is important to difference
between chitosan and cellulose, where three -OH groups of nearly
equal reactivity are available [23,24]. In industrial applications,
several solids having pores close to molecular dimensions
(micropores < 20 Å) are used as selective adsorbents because
of the physicochemical specificity they display towards certain
molecules in contrast to the mesoporous substrates (20-500 Å) and
macropores (> 500 Å). Adsorbents with these selective properties
include activated carbon among others [25]. Chitosan-based highly
activated carbons have also application for hydrogen storage [26].
In principle, electronic structure of diatomic molecules has been
built through the overlapping knowledge of the interacting atomic
orbitals [27]. In this case, the orbitals correspond to bonding (σg,
πg) and antibonding (σu, πu) orbitals of hydrogen, carbon, nitrogen
and oxygen diatomic molecules, whose H2, C2, N2, and O2 groundstate
electronic configurations are 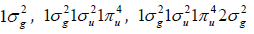 and
and 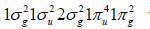 with 2, 8, 10 and 12 valence electrons,
respectively. Actually, the reactivity sites in a molecule correspond
to the highest occupied molecular orbitals (HOMO) and lowest
unoccupied molecular orbitals (LUMO). HOMO as base (donor), and
LUMO as acid (acceptor) are particularly important MOs to predict
reactivity in many types of reaction [28,29]. Activated carbon and
chitosan have been independently applied as sorption materials to
increase environmental quality standards. Then, we expect AC-Ch
nanocomposite to have a powerful handleable adsorption property
of pollutants that can be applied not only in wastewater treatment,
but also in medicine against intoxication, in batteries to increase
storage capacity, in electrodes of fuel cells, and in more possible
applications, according to the pore size distribution to be generated
on this new material.
with 2, 8, 10 and 12 valence electrons,
respectively. Actually, the reactivity sites in a molecule correspond
to the highest occupied molecular orbitals (HOMO) and lowest
unoccupied molecular orbitals (LUMO). HOMO as base (donor), and
LUMO as acid (acceptor) are particularly important MOs to predict
reactivity in many types of reaction [28,29]. Activated carbon and
chitosan have been independently applied as sorption materials to
increase environmental quality standards. Then, we expect AC-Ch
nanocomposite to have a powerful handleable adsorption property
of pollutants that can be applied not only in wastewater treatment,
but also in medicine against intoxication, in batteries to increase
storage capacity, in electrodes of fuel cells, and in more possible
applications, according to the pore size distribution to be generated
on this new material.
Methodology
The interaction between an activated carbon molecule (AC) and a unit of the chitosan copolymer (Ch) is studied by means of DFTDMol3 [30-32]. The AC system is a hypothetical model of two parallel linear chains of 24 carbons each one geometrically optimized using DFT, converging into a plane molecular carbon system. In this system six nodes were formed allowing 7 interconnected rings of different bond lengths and sizes: 2 of 6 carbons, 4 of 8 carbons and one of 16 carbons. By summing these quantities gives 54 carbons since the carbons are in the nodes double counted. When subtracted they are the 48 carbons of the AC system. This system has a length of 28.4Å comparable to that of the chitosan copolymer unit (Ch). The reactants are AC + Ch corresponding to C48 + C14H24N2O9.
Single point potential energy curves were constructed [1,2] by using smearing. The following conditions to find AC+Ch (Activated Carbon+Chitosan) interaction energy are: functional GGA-PW91 [31,33-36], unrestricted spin, dnd bases, and orbital occupation with various smearing values. Considering that we obtained a solution for the energy value convergence, the interaction by changing the smearing value was studied. Since electrons occupy orbitals with lower energies and integral occupation numbers in calculations of density functional, a smearing change indicates fractional occupation and virtual orbital within this occupation space [19]. When generating a fractional occupation, virtual orbitals are in this occupation space generated, if the HOMO-LUMO gap is small, and there is certain density near the Fermi level [1], then it is implemented the fractional occupation term kT. This pattern of fractional occupation depends on temperature. Covalent connectivity calculations [37] according to DMol3 on no-bonding to s- and f-shell scheme, bond type, and converting representation to Kekulé, for bond length tolerances from 0.6 to 1.15 Ǻ were accomplished in this molecular complex mostly composed of carbon. Area calculations have been carried out by inserting triangles in each amorphous carbon ring and using the
Heron formula: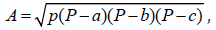 where P=(a+b+c)/2
is the perimeter of a triangle of a, b, c sides; while the pore size
diameter (PSD) is calculated as an approximation to the circle area.
Periodic systems can be constructed using amorphous builder
of BIOVIA Materials Studio, these are useful to calculate Radial
Distribution Functions and the area under the curve on a significant
interval.
where P=(a+b+c)/2
is the perimeter of a triangle of a, b, c sides; while the pore size
diameter (PSD) is calculated as an approximation to the circle area.
Periodic systems can be constructed using amorphous builder
of BIOVIA Materials Studio, these are useful to calculate Radial
Distribution Functions and the area under the curve on a significant
interval.
Results
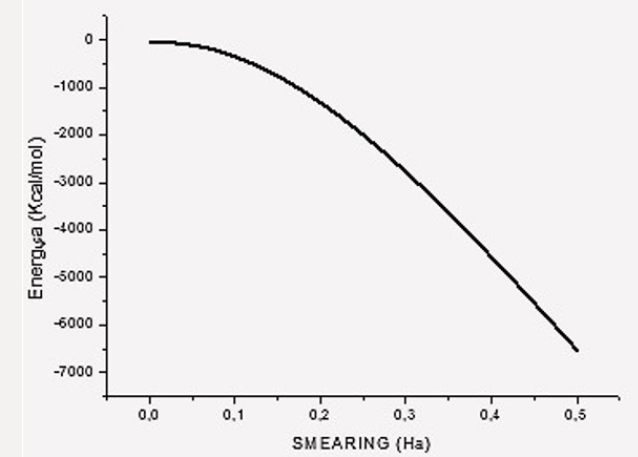
Chitosan Optimized by Applying Smearing
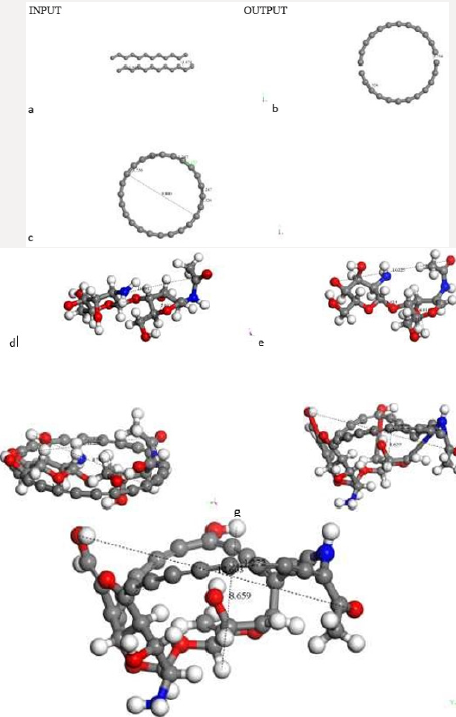
The default smearing value of 0.005Ha corresponds to T=1578.87 K and P=224.806 atm. We now exhibit electron smearing behavior using the known Fermi-Dirac statistic [38]. Facing two hydrogen atoms and using geometry optimization calculations, we built energy as a function of smearing value. Figure 1 shows the total energy variation when the system is optimized with respect to smearing value [39] (Figure 1). The fractional occupational pattern depends on the temperature, and this is derived from the energy change of Fermi distribution [6] as: 𝛿𝐸 = 𝑇𝑘; where k is Boltzmann constant. Considering a model in which the electrons are free and given that clouds of electrons are being a Fermi gas considered. The pressure is: 2/3 δE/δV [38]. From the latter two previous equations, temperature and pressure change is observed in Table 1 given the 𝛿𝐸 smearing energy. The planar molecular hypothetical system of 48 carbons is built by applying geometry optimization at two linear chains of 24 carbons as shown in Figure 2a, and the chitosan copolymer molecular system is built without applying geometry optimization, as observed in Figure 2b. Approaching enough these two molecular systems we studied a new molecular complex at different smearing values. The molecular model of carbon is symmetrically arranged in planar geometry, and it is physically activated through geometry optimization. We called activated carbon (AC) to the resulting planar carbon system. The length of this planar system is comparable to that one of chitosan (Ch). Each six-carbon ring has an area 4.34 Å2, each eight-carbon ring along with this has an area 8.74 Å2, each eight-carbon ring along with the sixteen-carbon ring has an area 8.55 Å2, and the sixteencarbon ring has an area 27.32 Å2. Considering each one of this area as circle areas the pore size diameter distribution is from 2.35 Å to 5.9 Å, which correspond to micropore size distribution of this carbon system. When considering the whole area of this system for calculating the pore size diameter 9.48 Å [40,41]. Chitosan is very well known to be macropore size [42] (Figure 2
Figure 2: C48 Carbon and Chitosan molecular systems. a) Input-Output of a C48 carbon system geometry optimization. Carbon atoms in gray color. b) Chitosan molecule (C14H24N2O9) without optimization. Hydrogen atoms in white color, Nitrogen in blue color and oxygen in red color.
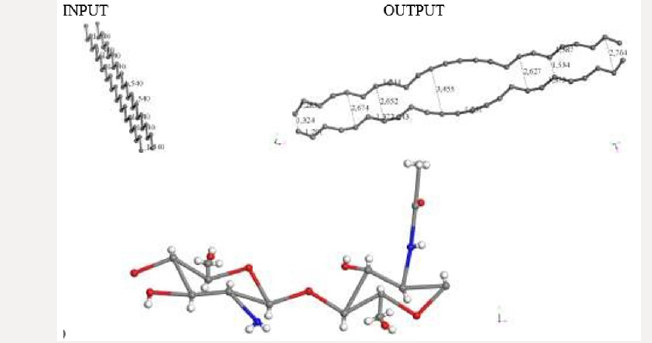
Figure 3: INPUT for interaction among activated carbon (AC) and one copolymer unit of Chitosan (Ch). a) Chitosan without geometry optimization. b) Potential energy curve with well depth of 30Kcal/mol for smearing: 0.05Ha. c) Potential energy curve with well depth of -1089 kcal/mol for smearing of 0.03 Ha.
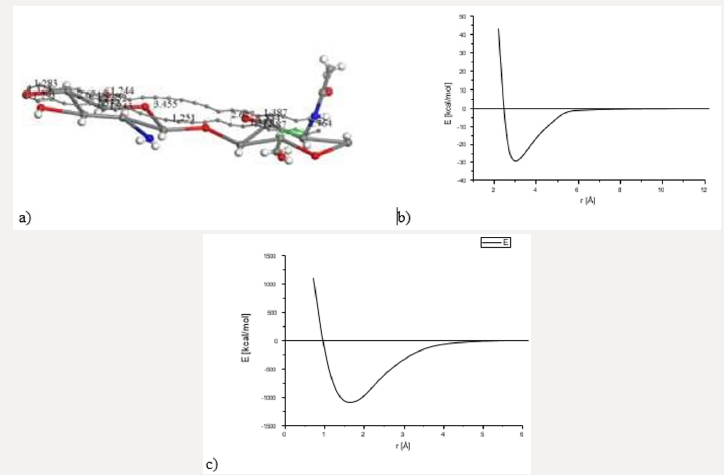
Searching for a new molecular complex, Figure 3 exhibits the potential energy curve of the interaction between AC and Ch having equilibrium at (1.6Å, -1089Kcal/mol). In this case chitosan was not geometrically optimized in order to build the potential energy curve observed in Figures 3b & 3c. It was really easy to build this curve using smearing energy 0.05 Ha for every single point calculated, and hard to build it at 0.03 Ha. We also tried lower values than this, and we obtained poor or none results (Figure 3). After applying geometry optimization at smearing 0.05 Ha, and subsequently at 0.03 Ha. The smearing at 0.02 Ha is shown in Figure 4a. Then, we built the potential energy curve as shown in Figure 4b in step by step single point calculations for AC + Ch face to face interaction, when 2.264 Å is the separation between their corresponding centers of mass. The latter has a potential well depth of 165 Kcal/ mol at a distance of 2.2 Å, meaning formation of a new molecular complex at an adsorption energy greater than 20 kcal/mol in the chemisorption range [43] (Figure 4). Covalent connectivity [37] to the resulting system in Figure 4a was applied under the conditions previously mentioned in methodology, and the molecular complex observed in Figure 5 is obtained. In this complex the reactants and products are C48 + C14H24N2O9 and C49H3O3 + CH2 + C4H6O2 + CH3NO + C2H2O + CH2O + C2H2 + CHNO + CH3, respectively. Carbon bonds are single, double, and triple, as an example the C12 ring has eight double bonds, one triple bond, and three single bonds, where all the carbon valence electrons are shared. Furthermore, C8 and C16 rings have double bonds in one side of the ring, and single and triple bonds in the other side; and C6 ring has four double bonds and two single bonds. This whole carbon system has been activated by chitosan, and double bonds, and single and triple bonds are the representative characteristics of carbine-type molecules (Figure 5).
Figure 4: OUTPUT for interaction among activated carbon (AC)and one copolymer unit of Chitosan (Ch) after DFT geometry optimization using smearing at 0.02Ha.
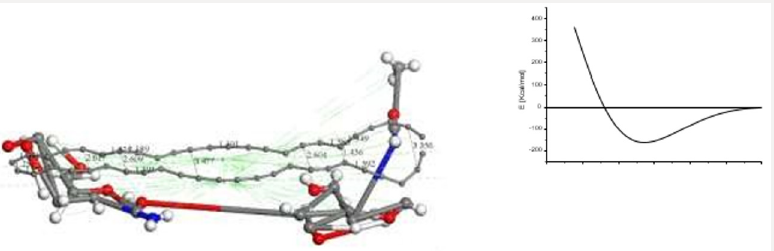
Figure 5: Connectivity applied after geometry optimization of CA+ Ch interaction (smearing at 0.02 Ha)
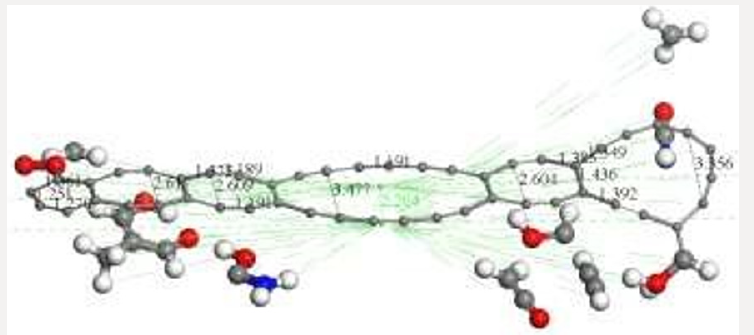
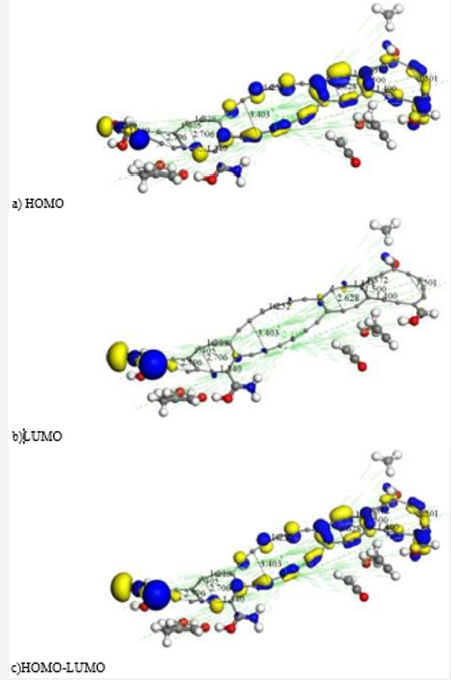
It must be noticed that geometry optimization of this whole system provides a lowest unoccupied molecular orbital (LUMO - electron acceptor) receiving an electron pair from the highest occupied molecular orbital (HOMO - electron donor). The donor HOMO from the base and the acceptor LUMO from the acid, combine with a molecular orbital bonding, which in our case corresponds to the orbitals 242-HOMO for E=-0.18317 Ha and 243-LUMO for E=- 0.17786, for a Fermi energy of -3136.28 Ha with A as irreducible representation of symmetry C1. The total orbitals number is 274. The orbital occupation is 202 A (2) plus 78 electrons in 65 orbitals, for a total number of 482 active electrons and binding energy of -22.997 Ha, at 2 steps. However, in order to get HOMO and LUMO drawn in this model, we run an energy calculation. Then, this molecular complex as seen in Figures 6a & 6b has HOMO-484 with E=-0.16398 Ha, LUMO-485 E=-0.16196 Ha, and Fermi energy Ef = -3161.44 Ha, for the reactivity sites with 482 active electrons. The total number of valence orbitals is 1070. The orbital occupation is 206 A (1) alpha and 206 A (1) beta, and 35.00 alpha electrons in 62 orbitals plus 35 beta electrons in 62 orbitals. HOMO as base-donor, and LUMO as acid-acceptor are the MOs locating possible reactivity in this reaction. An acid-acceptor can receive an electron pair in its lowest unoccupied molecular orbital from the base-donor highest occupied molecular orbital. That is to say, the HOMO from the base and the LUMO from the acid combine with a bonding molecular orbital in the ground state see Figure 6c.
Figure 6: We applied highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) to the previous AC+Ch molecular complex. a) HOMO. b) LUMO. c) HOMO-LUMO. Blue and yellow isosurfaces of the HOMO and LUMO denote positive and negative wave function phases, respectively.
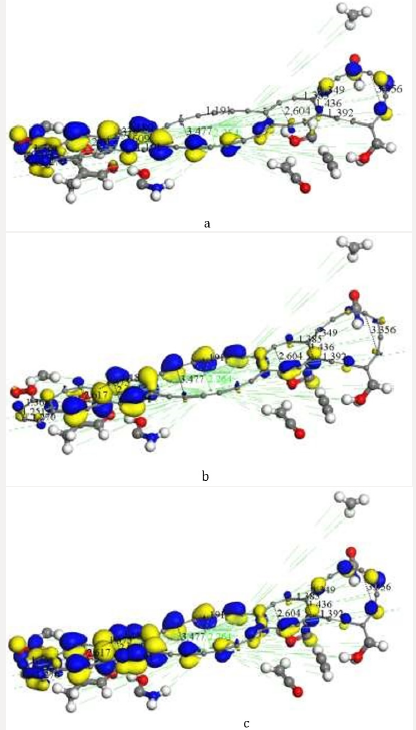
Figure 7: After covalent connectivity and another geometry optimization at smearing 0.02 Ha we mostly obtain highest occupied molecular orbitals a) HOMO; and we scarcely obtain lowest unoccupied molecular orbitals b) LUMO. The most molecular orbitals c) HOMOLUMO correspond to bonds of carbon atoms.
After applying covalent connectivity [37] to the resulting system in Figure 6, we again applied geometry optimization for smearing 0.02Ha, and we obtain different molecular orbitals in the results, as shown in Figure 7. This molecular complex as seen in Figure 7 has HOMO-482 with E=-0.17650 Ha, LUMO-483 E=0.16060 Ha, and Fermi energy Ef = -3162.004 Ha, for the reactivity sites with 482 active electrons. The orbital occupation is 204 A (1) alpha and 204 A (1) beta, and 37.00 alpha electrons in 62 orbitals plus 37 beta electrons in 62 orbitals. The molecular complex observed in Figure 7 has the same products previously mentioned. It must be noticed that the lowest unoccupied molecular orbitals (LUMO-acceptor) only draw orbitals in the CH3 product, the rest of the molecular orbitals correspond to the highest occupied molecular orbitals (HOMOdonor) complex. Then, this is a very stable molecular system only allowing reactivity through the methyl radical CH3 (Figure 7) The potential energy curve in Figure 3b is very near to physisorption; however, smearing energy in this case corresponds with a very high temperature, which actually occurrs little inside sun surface. In this work, we gradually get down smearing energy searching until reaching the glass transition temperature of chitosan. The smearing energy value 0.02 Ha corresponds with temperature 6315.49 K according to Table 1, and it is still too high; however, is this way we have been achieving geometry optimization to reach right smearing values according to experimental measurements. After successful convergence in geometry optimizations at 0.01, 0.007, 0.005, 0.003, and 0.002 smearing energies, the convergence at smearing energy 0.0017 Ha has been unsuccessful after more than 10000 SCF iterations for an oscillating energy with an energy tolerance of 0.00002 Ha. After these calculations, we continued rising the smearing energy until 0.00175, and after more than 5000 SCF, convergence is successfully accomplished. The temperature 552.6 K reached for smearing at 0.00175 agrees with glass transition temperature range [498.15K, 553.15K] of chitosan, according to experimental measurements [20-22].
Table 1: Change of temperature and pressure due to smearing variation 𝛿𝐸[𝐻𝑎] at temperature T [K] and pressure P [atm], for a volumen of 638 Å3.
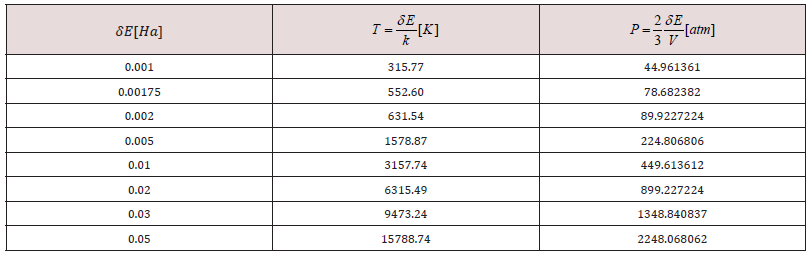
Figure 8 illustrates the final stage of the molecular complex formed. We can observe that while C48 has been deformed mainly in its planarity, the chitosan ended broken in the two initial groups of each polymer, also apparently divided in several smaller molecules. This fact is very well known experimentally, because one bonding solution (epichlorhydrine, glutaraldehyde, or EGDE -ethylene glycol glycidyl ether-) is commonly used to keep chitosan copolymer cross-linked for enhancing the resistance of sorbent beads against acid, alkali, or chemicals [19]. The products observed by applying covalent connectivity (under the bonding scheme for no bonding to s- and f- shell, covalent connectivity and bond type, and converting representation to Kekulé) are the following: C51H7NO4 + C4H6O2 + C2H2O + C2H2 + CH3O + CHNO + CH3. As it can be seen part of each polymer remain bonded to the AC system (Figure 8). Then, at smearing 0.00175 Ha we mostly obtain highest occupied molecular orbitals for the molecular complex observed in Figure 9. This output exhibits the orbitals a) HOMO-482 with an eigenvalue of -0.17013 Ha, b) LUMO-483 with an eigenvalue of -0.16923 Ha, and c) HOMOLUMO. The Fermi energy is Ef = 3162.0047053 Ha, for the reactivity sites with 482 active electrons. The orbital occupation is 238 A (1) alpha and 239 A (1) beta, and 2.96 alpha electrons in 5 orbitals plus 2.04 beta electrons in 4 orbitals (Figure 9)
Figure 8: OUTPUT of the AC+Ch interaction after geometry optimization using smearing at 0.00175 Ha, corresponding to 552.6 K and 78.68 atm according to Table 1.
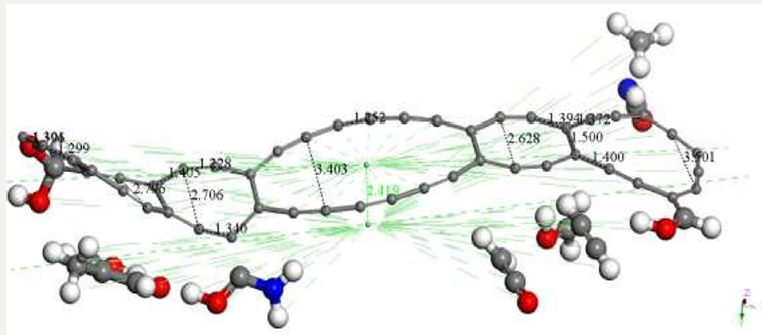
Figure 9: After another geometry optimization at smearing 0.00175 Ha: a) we mostly obtain highest occupied molecular orbitals HOMO, b) we scarcely obtain lowest unoccupied molecular orbitals LUMO, c) the greatest part of molecular orbitals HOMOLUMO correspond to bonds of carbon atoms.
Chitosan Optimized Without Smearing
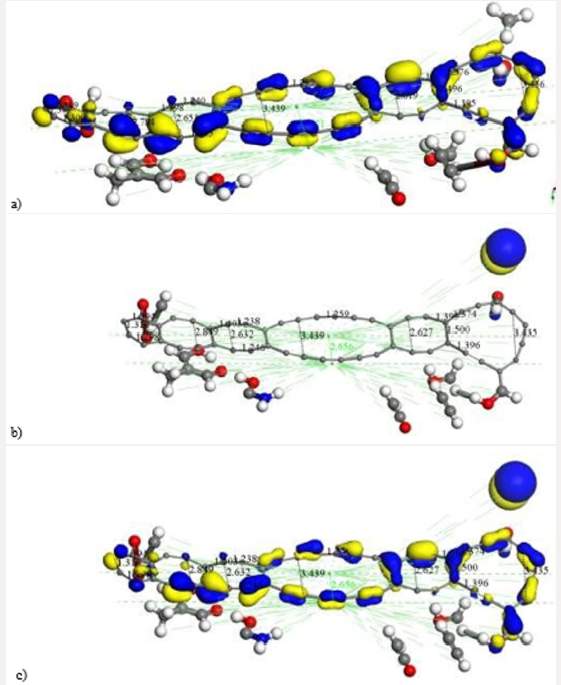
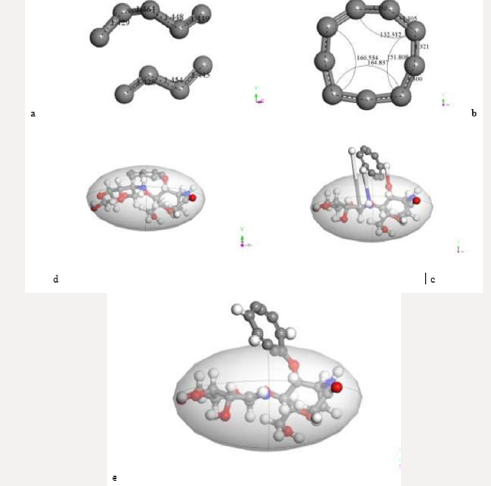
First of all, the C24 carbyne-type ring alternating single and triple bonds is obtained by applying connectivity [37] and bond type to a C24 carbon ring which is the output of the input shown in Figure 10a corresponding to the geometry optimization of two hypothetical C12-carbon chains (Figure 10b). Then, Figure 10c exhibits an alternating single and triple bonds C24-ring. Second, applying clean of BIOVIA Materials Studio on chitosan copolymer molecule designed in Figure 2b, we obtain the input of a chitosan copolymer molecule as in Figure10d, and the Output exhibiting geometry optimization of the previous molecule is shown in Figure 10e. As we can observe, in this case chitosan remained complete. We made this, after suspecting that the initial bonds lengths and angles were not right in our design of chitosan, because broken chitosan is not a satisfactory result. Then, mixing the optimized C24 and Ch systems as shown in Figure 10f in the Input of a C24-ring surrounding a chitosan copolymer molecule, and after applying geometry optimization we obtain the Output of the previous CA-Ch nanocomposite see Figure 10g. Finally, we applied bonding scheme criteria as in Figure 10h.The nanocomposite in Figure 10h is a good example of the possibility of modifying the pore size distribution of chitosan when it is embedded into activated carbon. Here we consider INPUT and OUTPUT for applying geometry optimization on activated carbon and chitosan C14H24N2O9 system after each part has been previously optimized, and we also applied bond criteria for connectivity, bond type and kekulé representation. The C24-ring is carbyne type, and the chitosan copolymer molecule has been optimized in three dimensions in this case. The position of C24- ring surrounding a chitosan copolymer molecule has been only proposed.
Figure 10: Here we consider INPUT and OUTPUT of the corresponding geometry optimization, and also applying bond criteria for connectivity, bond type and Kekulé representation. a) Input among two hypothetical C12-carbon chains. b) Output showing a disconnected C24-ring. c) The previous C24-ring linked using bond criteria. d) Input of a chitosan copolymer molecule. e) Output exhibiting the optimization of the previous molecule. f) Input of a C24-ring surrounding a chitosan copolymer molecule, g) Output of the previous CA-Chitosan, h) Bonding criteria applied to the previous output
From the interaction through geometry optimization of two linear carbon chains of four and five carbon atoms as in Figure 11a, cumulene C9-ring shown in Figure 11b is obtained. This is a clear evidence of Jahn-Teller effect, because we observe double bond lengths alternating long/short with a difference among .02 and .03 Å, and the angles in this non-planar (Figure 11b) cumulene molecule are also different. The expected angles in a planar symmetrical molecule should be the same according to a well-defined symmetry. We considered the interaction of chitosan with another almost planar carbon ring of nine carbon atoms, now one in front to the other as in Figure 11c. Then, in Figure 11d there is another example about building pore size distribution among chitosan and activated carbon. In this case, we consider INPUT and OUTPUT for geometry optimization of cumulene C9-ring and chitosan C14H24N2O9, each one previously optimized by applying geometry optimization to the whole system, and also considering the bond criteria for connectivity, bond type and Kekulé representation as shown in Figure 11e. The cumulene C9-ring and chitosan copolymer molecule have been optimized in three dimensions, and we clearly observe the cumulene passing from face to face to almost T-shape orientation taking three hydrogen atoms from chitosan. The input position of cumulene C9 ring face to face with chitosan in that precise location has been proposed, and the result has been excellent.
Figure 11: Here we consider INPUT and OUTPUT of the geometry optimization among a cumulene C9-ring and a Chitosan C14H24N2O9 molecule, and also applying bond criteria for connectivity, bond type and Kekulé representation. a) Input among a hypothetical C4- and C5- chains. b) Output showing a C9-ring. c) Input among the C9-ring and chitosan molecule. d) Output exhibiting the complex C9-ring into chitosan. e) Bonding criteria applied to the previous output.
Discussion
We consider each carbon ring as physically activated through geometry optimization, due to pore size diameter remains in the average size compared against experimental measurements [41]. The C48 optimized ring carbon-system and one non-optimized chitosan copolymer unit has been studied considering the result after geometry optimization, as a molecular complex obtained when smearing value changes for converging energy values. Different elongation among single and triple carbon bonds in the carbyne-type are due to Jahn-Teller effect [14]. Then, C24 carbynering when we optimize two carbon chains at 3.074 Å of separation distance, is due to the Jahn-Teller effect. The Jahn-Teller effect is also present in C48 carbinoid -ring for their C8- and C4- carbinoid -rings. Carbon rings C4N (N<~8) exhibit a substantial first-order Jahn-Teller distortion that leads to long/short (single/triple) bond alternation decreasing with increasing N [14]. Whether we want to draw HOMO-LUMO orbitals, it is necessary to ask for orbitals in the geometry optimization as input data. At this work, for smearing energy 0.02 Ha we found different HOMO LUMO orbital numbers among the initial system in Figure 5 without asking for orbitals in the geometry optimization calculation, and its output asking for orbitals in a new energy calculation shown in Figure 6. Again after practicing connectivity, bond type, and Kekulé representation at smearing energy 0.02 Ha, we asked for orbitals, and we found in Figure 7 a small change at the orbital numbers previously obtained, and the corresponding energies were little different to the previous ones. We infer that bonding type change produced the differences, and the correct values correspond to the correct bonding type in the new molecular complex system formed.
The strongly dependence on smearing means very closely spaced energy levels (high degeneracy) near Fermi level. When there is a degenerate electron state, any symmetrical position of the nuclei (except when they are collinear) is unstable. As a result of this instability, the nuclei move in such a way that the symmetry of their configuration is destroyed, the degeneracy of the term is being completely removed [44,45]. High degeneracy indicates a high symmetry of the molecule, then the system tends to be distorted, in such way that when moving, the occupied levels are down and the unoccupied ones are up [46]. When levels are very densely spaced, convergence is hard to reach, since very small changes will occupy completely different states, and we get oscillations. These can be damped by smearing out the occupancy over more states, so that we turn off the binary occupancy of the states. We get down smearing width to glass transition temperature by decreasing the smearing parameter in steps to gradually stabilize our molecular complex system at the right temperature.
We initially observe distortion of chitosan system, and then its possible breaking in some products. This is partially in agreement with the results presented by Chigo et al. [46] in a study of the interaction among graphene-chitosan for a relaxed system doped with boron, in which they consider the interaction of pristine graphene with the monomer of chitosan (G + MCh:C6H13O5N) in different configurations, whereas we consider a chitosan copolymer molecule: C14H24N2O9 in only one orientation. While Chigo et al. [46] found a perpendicular chitosan, molecule linked to a carbon nanotube system, we obtained a cumulene carbon ring almost perpendicularly linked to a chitosan copolymer molecule.
Conclusion
We found one mechanism to figure out an optimized big molecular complex system by using DFT geometry optimization. This mechanism is based on smearing calculations, and on decrements of smearing energy in the molecular complex system until reaching the glass transition temperature of one of the components, which in this case correspond to the chitosan copolymer molecule. In order to get a molecular complex system AC + Ch, it is needed a high temperature among them at least to the phase transition temperature of either AC or Ch, because when they are solids there is only a heterogeneous mixture at room temperature. The use of smearing allows to reach high temperatures because according to Table 1 temperature increases as the smearing energy increases. We observed that the use of smearing to optimize a molecule as complex as the chitosan causes this to be fractionated, nevertheless when putting it in a plate of coal we obtained the glass transition temperature of the chitosan reported experimentally. The potential well depth providing chemisorption indicates existence of phase transition in one of our two molecular systems. This phase change is attributed to chitosan, due to carbon is more stable, and because we reach glass transition temperature of chitosan when dealing with the whole molecular complex system. In addition, when applying covalent connectivity, the activated carbon is the most stable molecular system keeping its molecular structure. According to HOMO and LUMO in Figures 6 -9, the sites with the greatest reactivity correspond to double and triple bonds. Besides, Figure 9 exhibits one amine functional group linked to the carbon system now C51 carbon molecular complex formed with a particular pore size distribution. Considering that after geometry optimization physisorption provides bonding in two parts of the chitosan molecule, this is an indication of a more environmental linking than that caused by cross-linking solutions, because cross-linking solutions might be toxic in medicine applications. The first chitosan molecule used, and optimized using smearing resulted to be unstable, because finished broken in several products. The second chitosan molecule used, and optimized without smearing, or with a very small smearing value resulted to be very stable, on which we were able to add activated carbon and to obtain good results. We have been able to optimize chitosan and add activated carbon, and we have observed the change in pore size distribution, even though we are missing its calculation, to assign the type of material obtained (micropore, mesopore, or macropore). We are working on it.
References
- Morales AN, Pacheco JH (2010) Bonding of water to copper atom at an almost random interaction. Rev Mex Fís 56: 69-73.
- Zaragoza P, Pacheco JH, Echevarria I, Bravo A (2014) DFT study of interaction between a hydrogen molecule and AgY-zeolite. Rev Mex Fís 60: 460-465.
- Perdew JP, Wang Y (1992) Accurate and simple analytic representation of the electron-gas correlation energy. Phys Rev B 45: 13244-13249.
- Weinert M, Davenport JW (1992) Fractional occupations and densityfunctional energies and forces. Phys Rev B 45: 13709-13712.
- Delley B (1995) DMol, a standard tool for density functional calculations: Review and advances. In: Seminario JM, Politzer P (1st Edn.), Modern density functional theory: a tool for chemistry. Elsevier Amsterdam 2: 404.
- Janak JF (1978) Proof that ∂E∂ni=ε in density-functional theory. Phys Rev B 83: 7165-7168.
- Münster A (1969) Statistical thermodynamics. Vol I Springer, New York, USA.
- Mc Quarrie DA (1973) Statistical mechanics. Harper & Row, New York, USA.
- Michelini MC, Pis Diez R, Jubert AH (1998) A Density Functional Study of Small Nickel Clusters. Int J Quantum Chem 70: 693-701.
- Ye L, Freeman AJ, Delley B (1992) Local density functional study of the structural and electronic properties of C60 and XC60 (X=K, Rb, Cs). Chem Phys 160(3): 415-419.
- M Liu, VI Artyukhov, H Lee, F Xu, BI Yakobson (2013) Carbyne from First Principles: Chain of C Atoms, a Nanorod or a Nanorope. ACS Nano 7: 10075-10082.
- RH Baughmann (2006) Chemistry. Dangerously seeking linear carbon. Science 312: 1009-1110.
- H Ding, TW Schmidt, T Pino, F Güthe, JP Maier (2003) Towards bulk behaviour of long hydrogenated carbon chains? Phys Chem Chem Phys 5: 4772.
- Cataldo F (2005) Polyynes: Synthesis, Properties, and Applications (1st Edn.) CRC Press: Boca Raton pp. 528.
- Bylaska EJ, Weare JH, Kawai R (1998) Development of Bond-Length Alternation in Very Large Carbon Rings: LDA Pseudopotential Results. Phys Rev B 58: R7488-R7491.
- Torelli T, Mitas L (2000) Electron Correlation in C4N+2 Carbon Rings: Aromatic Versus Dimerized Structures. Phys Rev Lett 85: 1702-1705.
- Saito M, Okamoto Y (1999) Second-Order Jahn-Teller Effect on Carbon 4N+2 Member Ring Clusters. Phys Rev B 60(12): 8939-8942.
- Smisek M, Cerny S (1970) Active carbon: manufacture, properties and applications. Elsevier, New York, USA 12: 479.
- Rinaudo M (2006) Chitin and chitosan: properties and applications. Prog Polym Sci 31(7): 603-632.
- Guibal E, Milot C, Tobin J (1998) Metal-anion sorption by chitosan beads: equilibrium and kinetic studies. Ind Eng Chem Res 37(4): 1454-1463.
- Sakurai K, Maegawa T, Takahashi T (2000) Glass transition temperature of chitosan and miscibility of chitosan/poly (N-vinyl pyrrolidone) blends. Polymer 41(9): 7051-7056.
- Kadokawa JI (2014) In Han-Chan C, Hua-Chia C, Thomas S (1st Edn) Physical Chemistry of Macromolecules: Macro to Nanoscales, CRC Press, New Jersey, USA 13: 656.
- Cardona-Trujillo V (2012) (Spanish) Physicochemical and structural preparation and characterization of a chitosan-based conducting gel. Dissertation, Universidad del Valle, Santiago de Cali, Colombia.
- Rinaudo M, Reguant J (2000) Polysaccharide derivates. In: Frollini E, Leão AL, Mattoso LHC (eds) Natural polymers and agrofibers composites. CIPBRASIL, São Carlos Brésil, p.15-39.
- Wang C, Chang K, Chung T, Wu H (2004) Adsorption equilibria of aromatic compounds on activated carbon, silica gel, and 13x zeolite. J Chem Eng Data 49(3): 527-531.
- Wróbel-Iwaniec I, Díez N, Gryglewicz G (2015) Chitosan-based highly activated carbons for hydrogen storage. International Journal of Hydrogen Energy 40(17): 5788-5796.
- Atkins P, Friedman R (2005) Molecular Quantum Mechanics. (4th Edn.) Oxford University Press, New York, USA.
- Fukui K, Yonezawa T, Nagata C, Shingu H (1954) Molecular orbital theory of orientation in aromatic, heteroaromatic, and other conjugated molecules. J Chem Phys 22(8): 1433-1442.
- Lewis G (1923) Valence and the Structure of Atoms and Molecule. The Chemical Catalog Company, inc, USA pp. 172.
- BIOVIA Materials Studio (2017) Springer, New York, USA.
- Delley B (1998) An all‐electron numerical method for solving the local density functional for polyatomic molecules. J Chem Phys 92: 508-517.
- Auckenthaler T, Blum V, Bungartz HJ (2011) Parallel solution of partial symmetric eigenvalue problems from electronic structure calculations. Parallel Computing 37(12):783-794.
- Delley B (2000) From molecules to solids with the DMol3 approach. J Chem Phys 113(18): 7756-7764.
- Perdew JP (1991) Generalized gradient approximations for exchange and correlation: A look backward and forward. Physica B 172(1-2):1-6.
- Perdew JP, Wang Y (1986) Accurate and simple density functional for the electronic xchange energy: Generalized gradient approximation. Phys Rev B 33: 8800-8802
- Estrada E (2002) Physicochemical Interpretation of Molecular Connectivity Indices. J Phys Chem A 106: 9085-9091.
- Pathria RK (1972) Statistical Mechanics. Pergamon Press, New York, USA.
- Basiuk VA (2011) Electron smearing in DFT calculations: a case study of doxorubicin interaction with single-walled carbon nanotubes. Int J Quantum Chem 111: 4197-4205.
- Lozano Castelló D, Cazorla-Amorós D, Linares-Solano A (2002) Powdered Activated Carbons and Activated Carbon Fibers for Methane Storage: A Comparative Study. Energy & Fuels 16: 1321-1328.
- Pacheco Sánchez JH, Zaragoza-Rivera IP, Bravo-Ortega A (2017) Interaction of small carbon molecules and zinc dichloride: DFT study. Rev Mex Fís 63: 97-110.
- Khang G (2012) Handbook of Intelligent Scaffold for Tissue Engineering and Regenerative Medicine. CRC Press, Taylor and Francis, Boca Ratón, FL.
- Atkins P, De Paula J (2010) Using the Vapor Pressure of Pure Volatile Organic Compounds to Predict the Enthalpy of Vaporization and Computing the Entropy of Vaporization. Physical Chemistry. Freeman and Company, New York ,USA.
- Landau LD, Lifschitz EM (1977) Quantum Mechanics Nonrelativistic Theory. (3rd Edn), Pergamon Press, New York, USA, 3: 409.
- Jahn HA, Teller E (1937) Stability of Polyatomic Molecules in Degenerate Electronic States. I Orbital Degeneracy Proc R Soc London A 161: 220- 235
- Koppel H, Yarkony DR, Barentzen H (2009) The Jahn-Teller Effect: Fundamentals and Implications for Physics and Chemistry. Springer Series: Chemical Physics 97. Springer-Verlag, Berlin Heidelberg.
- Chigo Anota E, Torres-Soto A, Cocoletzi GH (2014) Studies of graphenechitosan interactions and analysis of the bioadsorption of glucose and cholesterol. Appl Nanosci 4: 911-918.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...