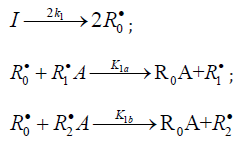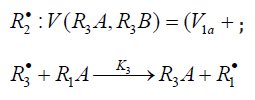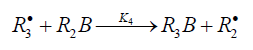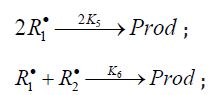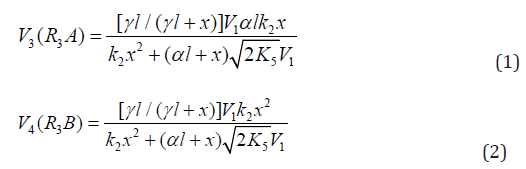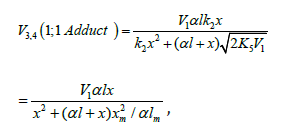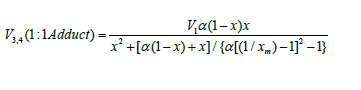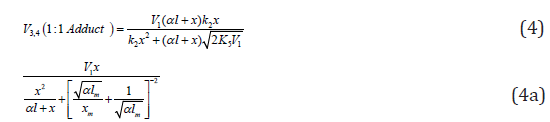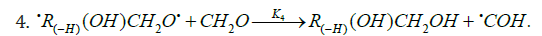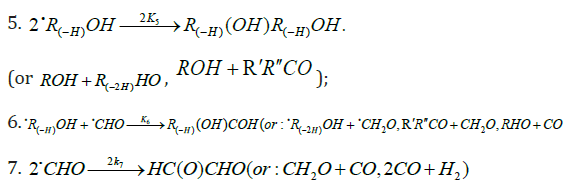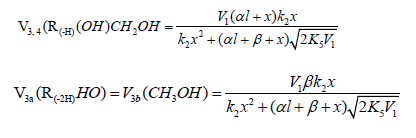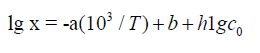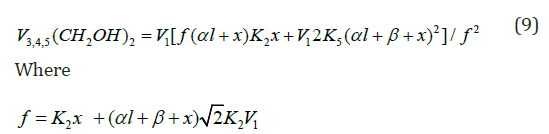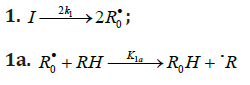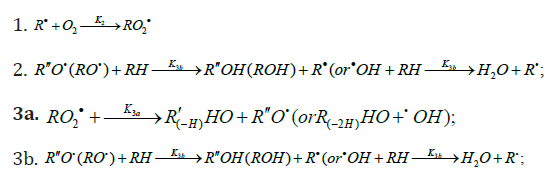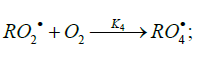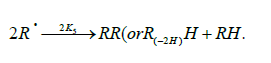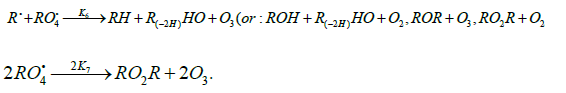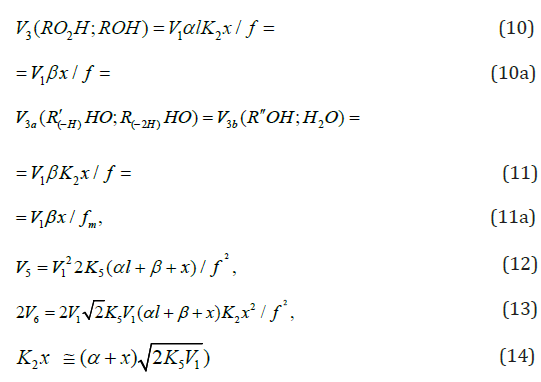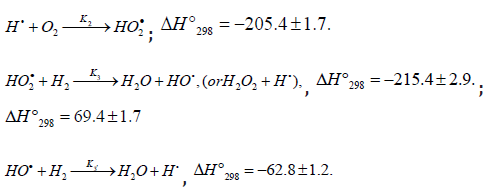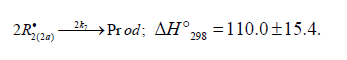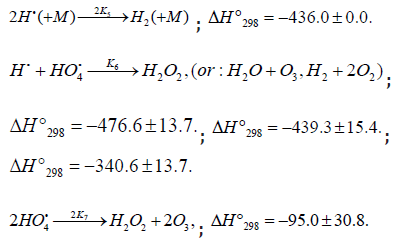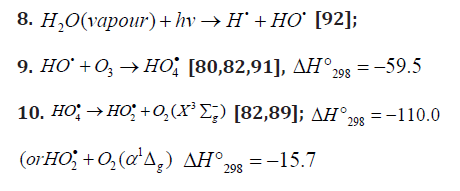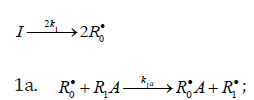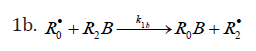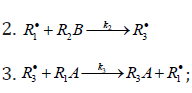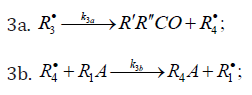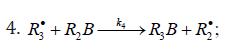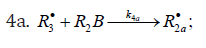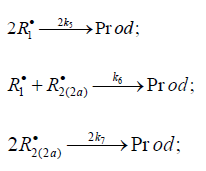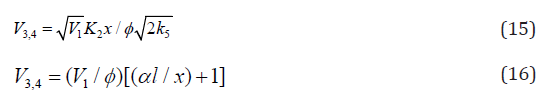Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2637-4609
Research Article(ISSN: 2637-4609) 
Kinetic Equations of Free-Radical Nonbranched- Chain Processes of Addition to Alkenes, Formaldehyde and Oxygen Volume 2 - Issue 5
Michael M Silaev*
- Chemistry Faculty, Lomonosov Moscow State University, Russia
Received: April 23, 2018; Published: May 17, 2018
*Corresponding author: Michael M Silaev, Chemistry Faculty, Lomonosov Moscow State University, Vorobievy Gory, Moscow 119991, Russia
DOI: 10.32474/AOICS.2018.02.000150
Abstract
The aim of this study was the conclusion of simple kinetic equations to describe ab initio initiated Nonbranched-chain processes of the saturated free-radical addition to the double bonds of unsaturated molecules in the binary reaction systems of saturated and unsaturated components. In the processes of this kind the formation rate of the molecular addition products (1:1 adducts) as a function of concentration of the unsaturated component has a maximum. Five reaction schemes are suggested for this addition processes. The proposed schemes include the reaction competing with chain propagation reactions through a reactive free radical. The chain evolution stage in these schemes involves three or four types of free radicals. One of them is relatively low-reactive and inhibits the chain process by shortening of the kinetic chain length. Based on the suggested schemes, nine rate equations (containing one to three parameters to be determined directly) are deduced using quasi-steady-state treatment. These equations provide good fits for the no monotonic (peaking) dependences of the formation rates of the molecular products (1:1 adducts) on the concentration of the unsaturated component in binary systems consisting of a saturated component (hydrocarbon, alcohol, etc.) and an unsaturated component (alkene, allyl alcohol, formaldehyde, or dioxygen). The unsaturated compound in these systems is both a reactant and an autoinhibitor generating low-reactive free radicals. A similar kinetic description is applicable to the Nonbranchedchain process of the free-radical hydrogen oxidation, in which the oxygen with the increase of its concentration begins to act as an oxidation autoingibitor (or an antioxidant). The energetics of the key radical-molecule reactions is considered.
Keywords: Low-reactive radical, Autoinhibitor, Competing reaction, Non branched-chain Addition, Thermochemical Data
Introduction
A free radical may be low-reactive if its unpaired p-electron may be delocalized, e.g., over conjugated bonds as in the case of allyl radical CH2=CHĊH2 or along a double bond from carbon to the more electron-affine oxygen as in the case of formyl radical HĊ=O. Note that the activity of a free radical is also connected to the reaction heat in which it participates. In Nonbranched-chain processes of reactive free radical (addend) addition to double bonds of molecules, the formation of rather low-reactive free radicals in reactions, which are parallel to or competing with propagation via a reactive radicals, lead to chain termination, because these lowreactive radicals do not participate in further chain propagation and because they de- cay when colliding with each other or with chaincarrier reactive radicals thus resulting in inefficient expenditure of the latter and process inhibition.
In similar processes involving the addend and inhibitor radicals in diffusion controlled bimolecular chain-termination reactions of three types, the dependences of the rate of mo- lecular 1:1 adduct formation on the concentration of the un- saturated component (which is the source of low-reactive free radicals in a binary system of saturated and unsaturated components) have a maximum, usually in the region of small (optimal) concentrations. The progressive inhibition of non- branched chain processes upon exceeding this optimal con- centration may be an element of self-regulation of the natural processes returning them to a steady state condition. Here, reactions of addition of reactive free radicals to multiple bonds of alkene, formaldehyde, and oxygen molecules to give 1:1 adduct radicals are taken as examples to consider the role of low-reactive free radicals as inhibitors of the non- branched chain processes at moderate temperatures. In the case of oxidation, there are tetraoxyl 1:2 adduct radical arising upon addition of a peroxyl 1:1 adduct radical to molecular oxygen at high enough concentrations of the latter.
The 1:1 adduct radical (which is the heaviest and the largest among the free radicals that result from the addition of one addend radical to the double bond of the molecule) may have an increased energy owing to the energy liberated in the transformation of a double bond into an ordinary bond (30-130kJ mol-1 for the gas phase under standard conditions [1-4]. Therefore, it can decompose or react with one of the surrounding molecules in the place of its formation without diffusing in the solution and, hence, without participating in radical-radical chain termination reactions. Which of the two reactions of the adduct radical, the reaction with the saturated component or the reaction with the unsaturated component, dominates the kinetics of the process will depend on the reactivity and concentration ratios of the components in the binary system.
Earlier [5,6], there were attempts to describe such peaking dependences fragmentarily, assuming that the saturated or unsaturated component is in excess, in terms of the direct and inverse proportionalities, respectively, that result from the simplification of a particular case of the kinetic equation set up by the quasi-steady-state treatment of binary copolymerization involving fairly long chains [5]. This specific equation is based on an irrational function, whose plot is a monotonic curve representing the dependence of the product formation rate on the concentration of the unsaturated component. This curve comes out of the origin of coordinates, is convex upward, and has an asymptote parallel to the abscissa axis. Replacing the component concentrations with the corresponding mole fractions generates a peak in this irrational function and thereby makes it suitable to describe the experimental data [7].
However, this circumstance cannot serve as a sufficient validation criterion for the mechanism examined, because the new property imparted to the function by the above artificial transformation does not follow from the solution of the set of algebraic equations that are set up for the reaction scheme accepted for the process in a closed system and express the equality of the steady-state formation and disappearance rates of the reactive intermediates. This publication presents a comprehensive review of the nonbranched-chain kinetic models developed for particular types of additions of saturated free radicals to multiple bonds [8-14]. It covers free radical additions to alkenes [10,11], their derivatives [8,9], formaldehyde (first compound in the aldehyde homological series) [8,9,12], and molecular oxygen [13,14] (which can add an unsaturated radical as well) yielding various 1:1 molecular adducts, whose formation rates as a function of the unsaturated compound concentration pass through a maximum (free radical chain additions to the С=N bond have not been studied adequately).
In the kinetic de-scription of these nontelomerization chain processes, the re-action between the 1:1 adduct radical and the unsaturated molecule, which is in competition with chain propagation through a reactive free radical (•PCl2, С2Н5CНОН, etc.), is included for the first time in the chain propagation stage. This reaction yields a low-reactive radical (such as СН2=С(СН3)CН2 or НC=О) and thus leads to chain termination because this radical does not continue the chain and thereby inhibits the chain process [8]. We will consider kinetic variants for the case of comparable component concentrations with an excess of the saturated component [10,11] and the case of an overwhelming excess of the saturated component over the unsaturated component [8,9,12]. Based on the reaction schemes suggested for the kinetic description of the addition process, we have derived kinetic equations with one to three parameters to be determined directly. Reducing the number of unknown parameters in a kinetic equation will allow one to decrease the narrowness of the correlation of these parameters and to avoid a sharp build-up of the statistical error in the nonlinear estimation of these parameters in the case of a limited number of experimental data points [15]. The rate constant of the addition of a free radical to the double bond of the unsaturated molecule, estimated as a kinetic parameter, can be compared to its reference value if the latter is known. This provides a clear criterion to validate the mathematical description against experimental data.
The kinetic equations were set up using the qua- si-steadystate
treatment. This method is the most suitable for processes that
include eight to ten or more reactions and four to six different free
radicals and are described by curves based on no more than three
to seven experimental points. In order to reduce the exponent of
the
2k5[ R1]2 term in the d[ R•1 ] / dt = 0 equation to unity[8], we used the
following condition for the early stages of the process: 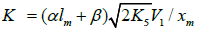 and, hence
and, hence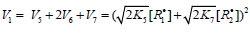 . Here, [R•1 ] and [R•2 ]
are the concentration of the addend radical and the low reactive
(inhibitor) radical, respectively. V1 is the initiation rate; V5, 2V6, and
V7 are the rates of the three types of diffusion-controlled quadraticlaw
chain termination reactions; 2k5 and 2k7 are the rate constants
of the loss of identical free radicals via the reactions. R•1 + R•1 and
R•2 + R•2 respectively; k6 is the rate constant of the loss of different
free radicals via the R•1+R•2 reaction (see Schemes 1-5). The kinetic
equations thus obtained fit the peaking rate curves well throughout
the range of unsaturated component concentrations in the binary
systems. Our mathematical simulation was based on experimental
data obtained for γ-radiation-induced addition reactions for which
the initiation rate V1 is known. The analysis of stable liquid-phase
products was carried out by the gas chromatographic method.
. Here, [R•1 ] and [R•2 ]
are the concentration of the addend radical and the low reactive
(inhibitor) radical, respectively. V1 is the initiation rate; V5, 2V6, and
V7 are the rates of the three types of diffusion-controlled quadraticlaw
chain termination reactions; 2k5 and 2k7 are the rate constants
of the loss of identical free radicals via the reactions. R•1 + R•1 and
R•2 + R•2 respectively; k6 is the rate constant of the loss of different
free radicals via the R•1+R•2 reaction (see Schemes 1-5). The kinetic
equations thus obtained fit the peaking rate curves well throughout
the range of unsaturated component concentrations in the binary
systems. Our mathematical simulation was based on experimental
data obtained for γ-radiation-induced addition reactions for which
the initiation rate V1 is known. The analysis of stable liquid-phase
products was carried out by the gas chromatographic method.
Addition to the С=С Bond of Alkenes and their Derivatives
When reacting with alkenes not inclined to free-radical polymerization, the free radicals originating from inefficient saturated telogens, such as alcohols [17] and amines [18], usually add to the least substituted carbon atom at the double bond, primarily yielding a free 1:1 adduct radical. This radical accumulates an energy of 90-130kJmol-1, which is released upon the transformation of the C=C bond to an ordinary bond (according to the data reported for the addition of nonbranched C1-C4 alkyl radicals to propene and of similar C1 and C2 radicals to 1-butene in the gas phase under standard conditions [1-4]. Such adduct radicals, which do not decompose readily for structural reasons, can abstract the most labile atom from a neighbor molecule of the saturated or unsaturated component of the binary reaction system, thus turning into a 1:1 adduct molecule. The consecutive and parallel reactions involved in this free-radical nonbranchedchain addition process are pre-sented below (Scheme 1). In the case of comparable compo- nent concentrations with a non over whelming excess of the saturated component, extra reaction (1b) ( 0) Ib K ≠ is included in the initiation stage [10,11]. In the case of an overwhelming excess of the saturated component reaction (1b) is ignored (KIb=0) = [8,9,12].
Comparable Component Concentrations
Scheme 1
Chain initiation
Chain propagation
Inhibition
Chain Termination
In this scheme, I is an initiator (e.g., a peroxide [5,12,13]); R•0 is a reactive (initiating) radical; A and B are hydrogen or halogen atoms [2,5,17-24]; R•1is •PCl2 [19], •CCl3 [20], alkyl [2,5], 1-hydroxyalkyl [5,6,17,22-24], or a similar functional- ized reactive addend radical [5]; R•2 is an alkenyl radical (allyl or higher) [2,5,17- 22], 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized low-reactive rad- ical (inhibitor) [5,18]; R•3 is a saturated reactive 1:1 adduct radical; R0A, R0B, and R1A are saturated molecules; R2B is an unsaturated molecule (alkene or its derivative); R3A and R3B are 1:1 adduct molecules; Prod designates the molecular products resulting from the dimerization or disproportionation of free radicals. The chain evolution (propagation and inhibi- tion) stage of Scheme 1 include consecutive reactions 2 and 3, parallel (competing) reaction pairs 3 and 4, and consecu- tive-parallel reaction pair 2-4.
The initiation reaction 1 is either the decomposition of a
chemical initiator [5,17,18] or a reaction induced by light [5,17,18]
or ionizing radiation [19-23]. The overall rate of chain initiation
(reactions 1, 1a, and 1b) is determined by the rate of the rate-limiting
step (k1b > k1a). The reaction between the free radical R•2 , which
results from reactions 1b and 4, and the saturated molecule R1А is
energetically unfavorable because it implies the formation of the
free radical R•1 , whichis less stable than the initial one. The addition
reaction 2 may be accompanied by the abstraction reaction 2a.
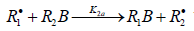 which yields the product R1B via a non chain
mechanism. Reaction 2a does not regenerate the addend radical R•1
and is not necessary for a kinetic description of the process, because
the rate ratio of reactions 2 and 2a, V2 /V2a = k2 /k2a is independent
of the concentration of the unsaturated component R2B in the
system. The inhibition of the non branched-chain addition process
is due to reaction 4, in which the adduct radical R•3 is spent in an
inefficient way, since this reaction, unlike reaction 3, does not
regenerate R•1 . The inhibiting effect is also due to the loss of chain
carriers R•1 through their collisions with low-reactive unsaturated
radicals R•2 , but to a much lesser extent.
which yields the product R1B via a non chain
mechanism. Reaction 2a does not regenerate the addend radical R•1
and is not necessary for a kinetic description of the process, because
the rate ratio of reactions 2 and 2a, V2 /V2a = k2 /k2a is independent
of the concentration of the unsaturated component R2B in the
system. The inhibition of the non branched-chain addition process
is due to reaction 4, in which the adduct radical R•3 is spent in an
inefficient way, since this reaction, unlike reaction 3, does not
regenerate R•1 . The inhibiting effect is also due to the loss of chain
carriers R•1 through their collisions with low-reactive unsaturated
radicals R•2 , but to a much lesser extent.
The rates of the formation (V, mol dm-3 s-1) of the 1:1 adducts R3A (via a chain mechanism) and R3B (via a non chain mechanism) in reactions 3 and 4 are given by the equations
where V1 is the rate of the initiation reaction 1; l = [R1A] and x= [R2B] are the molar concentrations of the initial components, with l > x; k2 is the rate constant of the addition of the R•1 radical from the saturated component R1А to the unsaturated molecule R2В (reaction 2); and γ = k1a/k1b and α = k3/k4 are the rate constant ratios for competing (parallel) reactions (α is the first chaintransfer constant for the free-radical telomerization process [5]).
The rate ratio for the competing reactions is V3/V4 = al/x, and the chain length is v = V3/V1.
Earlier mathematical simulation [8] demonstrated that replacing the adduct radical R3 with the radical R2 [5] in the reaction between identical radicals and in the reaction involving R1 gives rise to a peak in the curve of the 1:1 adduct formation rate as a function of the concentration of the unsaturated component. Reaction 1b, which is in competition with reaction 1a, is responsible for the maximum in the curve described by Eq. (2), and reaction 4, which is in competition with reaction (3), is responsible for the maximum in the curve defined by Eq. (1).
The number of unknown kinetic parameters to be determined
directly (k2, α, and γ) can be reduced by introducing the condition
γ ~= α, which is suggested by the chemical analogy between the
competing reactions pairs 1a-1b and 3-4. For example, the ratios of
the rate constants of the reactions of •OН, СН3О•, •СН3, NO•3 , and with
H2 PO•4 methanol to the rate constants of the reactions of the same
radicals with ethanol in aqueous solution at room temperature are
0.4-0.5 [25,26]. For the same purpose, the rate constant of reaction 2
in the kinetic equation can be replaced with its analytical expression
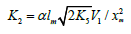 which is obtained by solving the quadratic equation
following from the reaction rate extremum condition which is
obtained by solving the quadratic equation following from the
reaction rate extremum condition ¶V3,4(1;1 Adduct ) = V3 + V4. After
these transformations, the overall formation rate equation for the
1:1 adducts R3A and R3B) (which may be identical, as in the case of
R3H [5,8,9,12,13,18-21]), appears as
which is obtained by solving the quadratic equation
following from the reaction rate extremum condition which is
obtained by solving the quadratic equation following from the
reaction rate extremum condition ¶V3,4(1;1 Adduct ) = V3 + V4. After
these transformations, the overall formation rate equation for the
1:1 adducts R3A and R3B) (which may be identical, as in the case of
R3H [5,8,9,12,13,18-21]), appears as
where lm and xm are the component concentrations l and x at the points of maximum of the function. Provided that V1 is known, the only parameter in Eq. (3a) to be determined directly is α. If V1 is known only for the saturated component R1A, then, for the binary system containing comparable R1A and R2B con-centrations, it is better to use the quantity λV1 , where λ = l/(l + x) is the mole fraction of R1A, in place of V1 in Eqs. (3) and (3a).
The two variable concentrations in the kinetic equation (3)
- l and x - can be reduced to one variable by replacing them with
the corresponding mole fractions. Substituting the expression
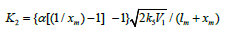 derived from the rate extremum
condition, into this transformed equation for the binary system
containing comparable component concen-trations, we obtain
derived from the rate extremum
condition, into this transformed equation for the binary system
containing comparable component concen-trations, we obtain
where 1 - χ = l/(l + x) and χ = x/(l + x) are the mole fractions of the components R1A and R2В (0 < χ <1), respectively, and χm is the χ value at the point of maximum. The overall formation rate of the 1:1 adducts R3A and R3B is a sophisticated function of the formation and disappearance rates of the radicals
Figure 1: Reconstruction of the functional dependences (curves) of the product formation rates V3, 4 (1, ) on the mole fraction of the unsaturated component (χ) from empirical data (symbols) using Eq. (3b) (model optimization with respect to the parameter α) for the phosphorus trichloride– methylpropene reaction system at 303K [19] (standard deviation of SY = 2.58 * 10–6) and (2, ○) on the concentration of the unsaturated component (x) from empirical data (symbols) using Eq. (4a) (model optimization with respect to V1, хm, and α) for the 2-propanol–2-propen-1-ol system at 433K [23] (SY = 5.91 10–7).
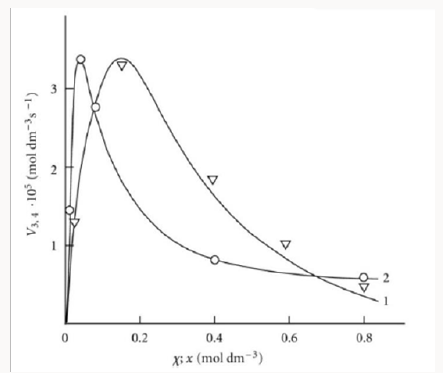
R•1 and R•2 :V(R3A,R3B)=(V1a+V3-V5)-(V1b+V4-V7). The application of the above rate equations to particular single nonbranched-chain additions is illustrated in Figure 1. Curve 1 represents the results of simulation in terms of Eq. (3b) for the observed 1:1 adduct formation rate as a function of the mole fraction of the unsaturated component in the phosphorus trichloride-methylpropene1 reaction system at 303K [19]. In this simulation, the 60Co γ-radiation dose rate was set at P = 0.01 Gy s-1 and the initiation yield was taken to be G(•PCl2) = 2.8 particles per 100eV (1.60 × 10-17 J) of the energy absorbed by the solution [19]. The product of reaction 3 is Cl2PCH2C(Cl)(CH3) CH3 (two isomers), V1 = 4.65×10-9 mol dm-3 s-1 at χ = 0, and 2k5 = 3.2 × 108 dm3 mol-1 s-1. This leads to α = (2.5 ± 0.4) × 103, and the rate constant of reaction 2 derived from this α value is k2 = (1.1 ± 0.2) × 104 dm3 mol-1 s-1.
Note that, if the R2-B bond dissociation energy for the unsaturated component of the binary system is approximately equal to or above, not below, the R1-A bond dissociation energy for the saturated component, then the rate of reaction 4 relative to the rate of the parallel reaction 3 (chain propagation through the reactive free radical R•1 ) will be sufficiently high for adequate description of R3A and R3B adduct formation in terms of Eqs. (1)-(3b) only at high temperatures [20]. In the phosphorus trichloride-propene system, the difference be-tween the R2-B (B = H) and R1-A (A = Hal) bond dissociation energies in the gas phase under standard conditions [1] is as small as 5kJ mol-1, while in the tetrachloro-methanemethylpropene (or cyclohexene) and bromoeth-ane-2-methyl- 2-butene systems, this difference is 20.9 (37.7) and ~24 kJ mol-1, respectively.
Excess of the Saturated Component
If the concentration of the saturated component exceeds the concentration of the unsaturated component in the binary system, reaction 1b can be neglected. If this is the case (k1b = 0), then, in the numerators of the rate equations for reactions 3 and 4 (Eqs. (1) and (2)), γ l / (γ l + x) = 1 and the overall rate equation for the formation of the 1:1 adducts R3A and R3B will appear as
where the parameters are designated in the same way as in
Eqs. (1)-(3a), l >> x, and 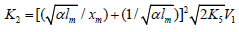 is determined
from the condition k ¶
V3, 4 (1:1 Adduct) / ¶x=0.
is determined
from the condition k ¶
V3, 4 (1:1 Adduct) / ¶x=0.
The rate equations for the chain termination reactions 5-7 (Scheme 1, k1b = 0) are identical to Eqs. (12)-(14) (see below) with β = 0.
Note that, if it is necessary to supplement Scheme 1 for k11 = 0 with the formation of R1B via the possible non chain reaction 2a (which is considered in the Section 2.1), the parameter K2a should be included in the denominator of Eq. (4) to obtain
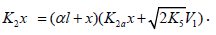
The analytical expression for k2 in the case of k2a¹0 is identical to the expression for k2 for Eq. (4). The equation for the rate k2a(R1B) can be derived by replacing K2 with k2a in the numerator of Eq. (4) containing k2a in its denominator. Curve 2 in Figure 1 illustrates the good fit between Eq. (4a) and the observed 1:1 adduct formation rate as a function of the concentration of the unsaturated component in the reaction system 2-propanol-2-propen-1-ol at 433K [8,9]. In this description, we used a 60Co γ-radiation dose rate of P = 4.47 Gy s-1 [23]. The product of reactions 3 and 4 is СН3(СН3) С(ОН)СН2СН2СН2ОН, and 2k5 = 1.0´1010 dm3 mol-1 s-1. The following parameters were obtained: V1 = (3.18 ± 0.4) × 106mol dm-3 s-1, xm = (3.9 ± 0.5) × 10-2mol dm-3, and α = (6.8 ± 0.8) × 10-2. The rate constant of reaction 2 derived from this α is k2 = (1.0±0.14)´105 dm3 mol-1 s-1.
Addition to the C=O Bond of Formal-dehyde
Free radicals add to the carbon atom at the double bond of the carbonyl group of dissolved free (unsolvated, monomer) formaldehyde. The concentration of free formaldehyde in the solution at room temperature is a fraction of a percent of the total formaldehyde concentration, which includes formalde-hyde chemically bound to the solvent [27]. The concentration of free formaldehyde exponentially increases with increasing temperature [28]. The energy released as a result of this addi-tion, when the C=O bond is converted into an ordinary bond, is 30 to 60Jmol-1 (according to the data on the addition of С1-С4 alkyl radicals in the gas phase under standard conditions [1-4]). The resulting free 1:1 adduct radicals can both abstract hydrogen atoms from the nearestneighbor molecules of the solvent or unsolvated formaldehyde and, due to its structure, decompose by a monomolecular mechanism including isom-erization [9,12].
Addition of Free 1-Hydroxyalklyl Radicals with Two or More Carbon Atoms
Free 1-hydroxyalkyl radicals (which result from the abstraction of a hydrogen atom from the carbon atom bonded to the hydroxyl group in molecules of saturated aliphatic alcohols but methanol under the action of chemical initiators [29,30], light [17,31], or ionizing radiation [32,33]) add at the double bond of free formaldehyde dissolved in the alcohol, forming 1,2-alkanediols [8,9,12,29-36], carbonyl compounds, and methanol [8,33] via the chaining mechanism. (The yields of the latter two products in the temperature range of 303 to 448K are one order of magnitude lower.) In these processes, the determining role in the reactivity of the alcohols can be played by the desolvation of formaldehyde in alcohol-formaldehyde solutions, which depends both on the temperature and on the polarity of the solvent [28,33]. For the γ-radiolysis of 1(or 2)-propanol-formaldehyde system at a constant temperature, the dependences of the radiation-chemical yields of 1,2-alkanediols and carbonyl compounds as a function of the formaldehyde concentration show maxima and are symbatic [8,32]. For a constant total formaldehyde concentration of 1mol dm-3, the dependence of the 1,2-alkanediol yields as a function of temperature for 303-473K shows a maximum, whereas the yields of carbonyl compounds and methanol in-crease monotonically [33] (along with the concentration of free formaldehyde [28]). In addition to the above products, the nonchain mechanism in the γ-radiolysis of the solutions of formaldehyde in ethanol and 1- and 2-propanol gives ethane-diol, carbon monoxide, and hydrogen in low radiation-chemical yields (which, however, exceed the yields of the same products in the γ-radiolysis of individual alcohols) [8,9,33]. The available experimental data can be described in terms of the following scheme of reactions:
Scheme 2:
Chain propagation
Inhibition
Chain termination
In these reactions, I is an initiator, e.g., a peroxide [29,30]; R•0 , some reactive radical (initiator radical); R, an alkyl; ROH, a saturated aliphatic alcohol, either primary or secondary, beginning from ethanol; CH2O, the unsaturated molecule - free formaldehyde; •СН2ОН, the 1-hydroxymetyl fragment radical; •R(-H)OH, the reactive 1-hydroxyalkyl addend radical, beginning from 1-hydroxyethyl; R(-H)(ОH)СН2О•, the reactive hydroxyalkoxyl 1:1 adduct radical; •СНО, the low-reactive formyl radical (inhibitor radical); R0H, the molecular product; R(-H)(OH)СН2ОН, 1,2-alkanediol; R(-2H)HO, an aldehyde in the case of a primary alcohol and an R’R”CO ketone in the case of a secondary alcohol; R(-H)(ОH)R(-H)ОH, a vicinal alkanediol; R(-H)(OH)CHO, a hydroxyl aldehyde. The chain evolution stage of Scheme 2 includes consecutive reaction pairs 2-3, 2-3a, and 3a-3b; parallel (competing) reaction pairs 3-3a, 3-3b, 3-4, and 3a-4; and consecutive-parallel reactions 2 and 4.
Scheme 2 does not include the same types of radi-cal-molecule reactions as were considered in Section 2.1 for Scheme 1. In addition, it seems unlikely that free adduct rad-icals will add to formaldehyde at higher temperatures the re-action of adding is unlikely because this would result in an ether bond. The addition of hydroxymethyl radicals to for-maldehyde, which is in competition with reaction 3b, is not included as well, because there is no chain formation of ethanediol at 303-448K [33]. At the same time, smallamounts of ethanediol can form via the dimerization of a small fraction of hydroxymethyl radicals, but this cannot have any appreciable effect on the overall process kinetics. The addition of free formyl radicals to formaldehyde cannot proceed at a significant rate, as is indicated by the fact that there is no chain formation of glycol aldehyde in the systems examined [33].
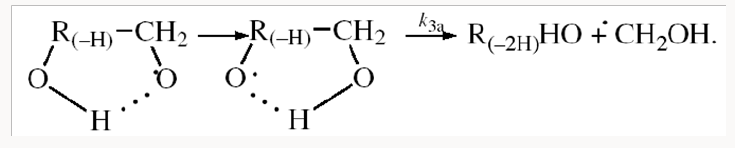
The mechanism of the decomposition of the free adduct radical via reaction 3a, which includes the formation of an intramolecular H···О bond and isomerization, can be repre-sented as follows [8,9,12]: (Picture 1)
The probability of the occurrence of reaction 3a should increase with increasing temperature. This is indicated by experimental data presented above [8,9,12]. The decomposition of the hydroxyalkoxyl radical. R(-H)(ОH)СН2О• (reaction 3a) is likely endothermic. The endothermic nature of reaction 3a is indirectly indicated by the fact that the decomposition of simple C2−C4 alkoxyl radicals RО• in the gas phase is ac-companiedby heat absorption: ( Δ298° =30−90kJmol-1 [2−4]). Reaction 3b, subsequent to reaction 3a, is exothermic, and its heat for C2−C3 alcohols in the gas phase is = Δ298° −40 to −60kJmol-1 [2-4]. As follows from the above scheme of the process, reactions 3a and 3b, in which the formation and consumption of the highly reactive free radical hydroxymethyl take place (at equal rates under steady-state conditions), can be represented as a single bimolecular reaction 3a,b occurring in a “cage” of solvent molecules.
The free formyl radical resulting from reaction 4, which is in competition with reactions 3 and 3a, is comparatively low-reactive because its spin density can be partially delocal-ized from the carbon atom via the double bond toward the oxygen atom, which possesses a higher electron affinity [1]. For example, in contrast to the methyl and alkoxyl π-radicals, the formyl σ-radical can be stabilized in glassy alcohols at 77K [37]. In the gas phase, the dissociation energy of the C-H bond in formyl radicals is half that for acetyl radicals and is about 5 times lower than the dissociation energy of the Сα-Н bond in saturated C1-C3 alcohols [1].
As distinct from reactions 3 and 3a,b, reaction 4 leads to an inefficient consumption of hydroxyalkoxyl adduct radicals, without regenerating the initial 1-hydroxyalkyl addend radi-cals. Reaction 4 together with reaction 6 (mutual annihilation of free formyl and chain-carrier 1-hydroxyalkyl radicals) causes the inhibition of the nonbranched-chain process. For the disproportionation of the free radicals, the heats of reac-tions 5−7 for C1−C3 alcohols in the gas phase vary in the range of = Δ298° -135 to -385kJmol-1 [1−4].
The rates of the chain formation of 1,2-alkanediols in reaction 3 (and their nonchain formation in reaction 4), carbonyl compounds in reaction 3a, and methanol in reaction 3b are given by the following equations:
As
where V1 is the initiation rate, l is the molar concentration of the saturated alcohol at a given total concentration of formal-dehyde2 dissolved in it, x is the molar concentration of free formaldehyde (l >> x), k2 is the rate constant of reaction 2 (addition of 1-hydroxyalkyl free radical to free formaldehyde), and α = k3/k4 and β = k3а/k4 (moldm-3) are the ratios of the rate constants of the competing (parallel) reactions. Estimates of 2k5 were reported by Silaev et al. [39,40]. From the extremum condition for the reaction 3a rate function, ∂V3a/ ∂ =0 derived the following analytical expression:
The overall process rate is a complicated function of the formation and disappearance rates of the •R(-H)OH and •СНО free radicals: V(R(-H)(OH)CH2OH, R(-2H)HO, CH3OH) = V1a + V3 + V3b - V4 - V5 + V7. The ratios of the rates of the competing reactions are V3/V4 = αl/x and V3a/V4 = β/x, and the chain length is ν = ( V3 + V3a)/V1. The ratio of the rates of formation of 1,2-alkanediol and the carbonyl compound is a simple linear function of x: V3, 4(R(-H)(OH)CH2OH)/ V3a(R(-2H)HO) = ( k4/ k3а)х + ( k3/ k3а)l. The equations for the rates of chain-termination reactions 5-7 are identical to Eqs. (12)-(14) (see below, Section 4.1).
Neutral formaldehyde solutions in alcohols at room temperature primarily consist of a mixture of formaldehyde pol-ymer solvates reversibly bound to alcohols; these polymer solvates differ in molecular mass and have the general formula RO(CH2O) nH, where n = 1-4 [27]. The concentration of for-maldehyde that occurs in solution as a free, unsolvated active species chemically unbound to the solvent (this species is capable of scavenging free radicals) at room temperature is lower than a percent of the total formaldehyde concentration [27]. The concentration x of the free formaldehyde species in solutions was determined by hightemperature UV spectro-photometry in the range 335-438 K at the total formaldehyde concentration c0 (free and bound species including the con-centration of polymer solvates) of 1.0-8.4moldm-3 in water, ethanediol, methanol, ethanol, 1-propanol, 2-propanol, and 2-methyl-2-propanol [28] (see Table of the Appendix). This concentration increases with temperature according to an exponential law, and it can be as high as a few percent of the total concentration in solution under the test conditions, up to 19.3% in the case of 2-methyl-2-propanol at a total concen-tration of 1.0mol dm-3 and a temperature of 398 K. The fol-lowing empirical equation relating the concentration x (mol dm-3) of free formaldehyde to temperature T (K) and the total concentration c0 in the solution (measured at room tempera-ture), was developed by the treatment of 101 data points [28,39]:
Appendix: The experimental concentrations x (mol dm-3) of free formaldehyde at different temperatures T (K) and total formalde- hyde concentrations c0 (mol dm-3) in various solvents.
where the coefficients a and b were calculated as the parameters of a straight-line equation by the least-squares technique from the dependence of lg x on 1/T at c0 = 1.0moldm-3 for various solvents, and the coefficient h was obtained as the average value of the slopes of lg x as linear functions of lg c0 at various series of fixed temperatures. The Appendix summarizes these coefficients for each solvent. As regards the experi-mental data, the error in the calculations of the concentration x of free formaldehyde made by Eq. (7) in the specified tem-perature range was no higher than 25%.
On the assumption that the dependence of the density of a given solution on the concentration of formaldehyde is similar to the analogous linear dependence found for aqueous for-maldehyde solutions (0-14mol dm-3; 291 K) [27], the con-centrations lT (mol dm-3) of alcohols in alcohol-formaldehyde solutions at a certain temperature can be estimated by the equation
where c0 is the total formaldehyde concentration (moldm-3); M is the molecular mass (gmol-1) of the solvent; d and dT are the solvent densities (gcm-3) at room and given temperatures, respectively; the coefficients 8.4×10-3 and 21.6 have the units of 103 g mol-1 and g mol-1, respectively [38].
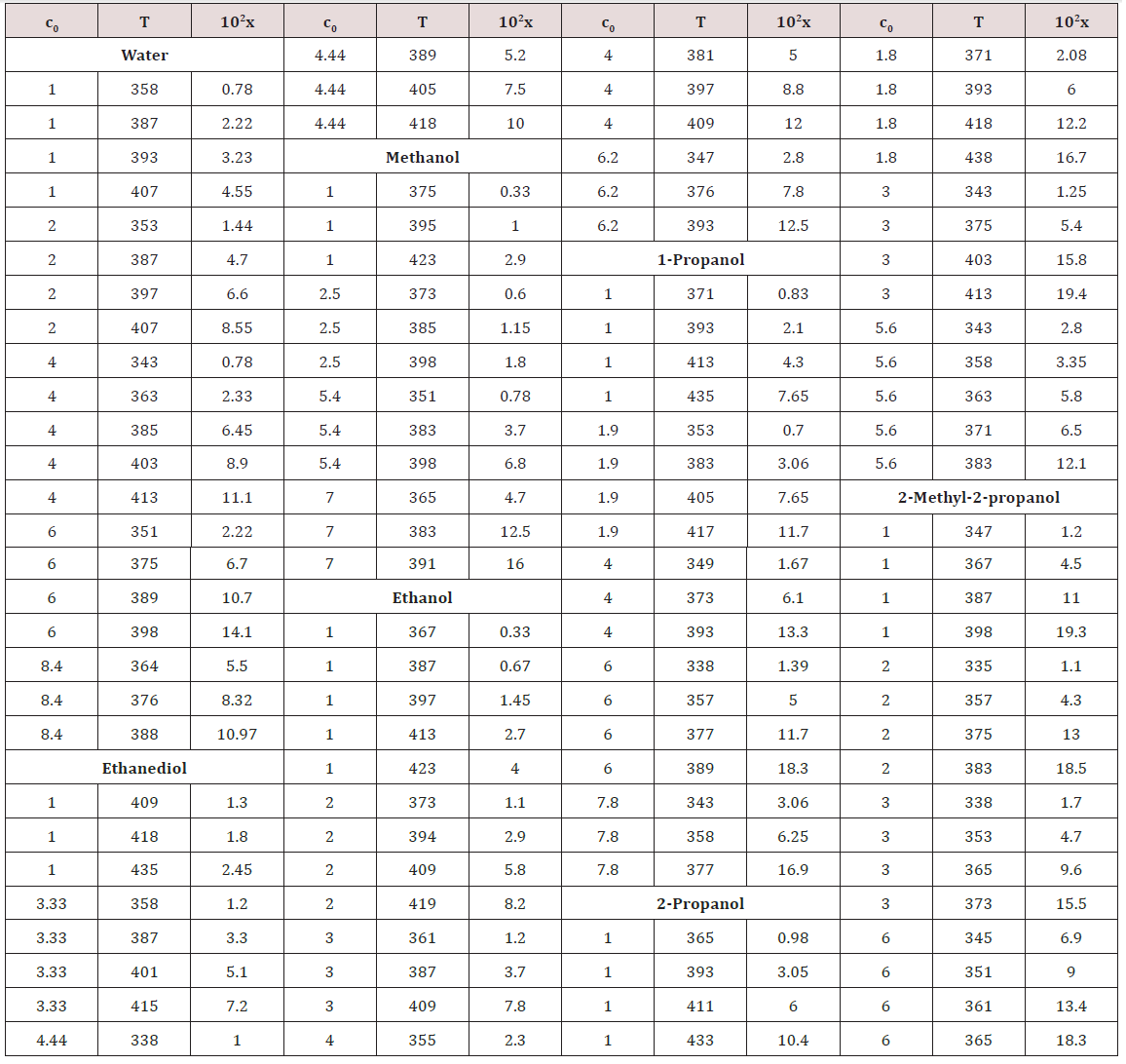
Earlier [28], it was found that the concentration x of the free formaldehyde species decreased with the solvent permittivity D298 at a constant temperature. Water is an exception. Alt-hough water is more polar than alcohols, the concentration x of free formaldehyde in an aqueous solution is anomalously high and reaches the level of its concentration in 2-propanol, all other factors being the same (see Figure 2) [28, 39]. This can be due to the specific instability of hydrated formaldehyde spe-cies and the ease of their conversion into free formaldehyde with increasing temperature.
Figure 2: Logarithmic plot of the experimental concentrations x(moldm-3) of free formaldehyde at its total concentration c0= 1.0 moldm-3 and 395±3K in () water, ( ) methanol, ( ) ethanol, (↓)1-propanol, (≤) 2-propanol, and (σ) 2-methyl-2-propanol as functions of the permittivity D298 of these solvents (+ refers to the concentrations xin the above solvents calculated by empirical Eq. (8)).
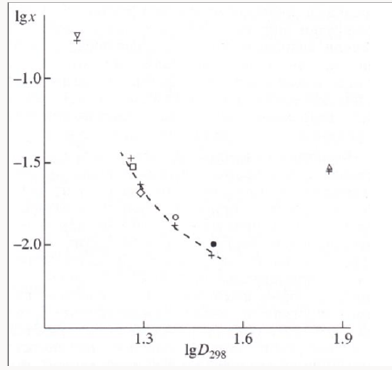
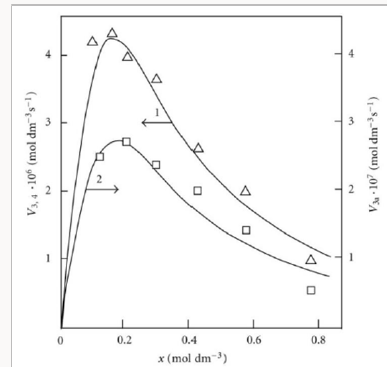
Figure 3 illustrates the use of Eqs. (5) and (6) for describing the experimental dependences of the formation rates of 1,2-butanediol (curve 1) in reactions 3 and 4 and propanal (curve 2) in reaction 3a on the concentration of free formal-dehyde in the 1-propanol-formaldehyde reacting system at a total formaldehyde concentration of 2.0 to 9.5mol dm-3 and temperature of 413K [8,9,41]. The concentration dependence of the propanal formation rate was described using the esti-mates of kinetic parameters obtained for the same dependence of the 1,2-butanediol formation rate. We considered these data more reliable for the reason that the carbonyl compounds forming in the alcohol-formaldehyde systems can react with the alcohol and this reaction depends considerably on the temperature and acidity of the medium [27]. The mathematical modeling of the process was carried out using a 137Cs γ-radiation dose rate of P = 0.8Gys-1 [32,41], a total initiation yield of G( CH3СН2ĊНОН) = 9.0 particles per 100 eV [8,9] (V1 = 4.07 × 10-7 moldm-3 s-1), and 2k5 = 4.7 × 109dm3 mol-1 s-1). The following values of the parameters were obtained: α = 0.36 ± 0.07, β = 0.25 ± 0.05 mol dm-3, and K2 = (6.0 ± 1.4) × 103dm3 mol-1 s-1.
Figure 3: Reconstruction of the functional dependence (curves) of the product formation rates V3,4 and V3а on the concentration x of free formalde-hyde (model optimization with respect to the parameters α, β and K2) from empirical data (symbols) for the 1-propanol–formaldehyde system at 413 K [8,9,41]: (1, ) calculation using Eq. (5), standard deviation of SY = 2.20 10–7; (2, □) calculation using Eq. (6), SY = 2.38 10–8.
Note that, as compared to the yields of 1,2-propanediol in the γ-radiolysis of the ethanol-formaldehyde system, the yields of 2,3-butanediol in the γ-radiolysis of the ethaetha-nol-acetaldehyde system are one order of magnitude lower [41]. Using data from [8,9], it can be demonstrated that, at 433 K, the double bond of 2-propen-1-ol accepts the 1-hydroxyethyl radical 3.4 times more efficiently than the double bond of formaldehyde [42].
Addition of Hydroxymethyl Radicals
The addition of hydroxymethyl radicals to the carbon atom at the double bond of free formaldehyde molecules in methanol, initiated by the free-radical mechanism, results in the chain formation of ethanediol [34]. In this case, reaction 3a in Scheme 2 is the reverse of reaction 2, the 1-hydroxyalkyl radical •R(-H)OH is the hydroxymethyl radical •СН2ОН, so reaction 3b is eliminated ( k3b = 0), and reaction 5 yields an additional amount of ethanediol via the dimerization of chain-carrier hydroxymethyl radicals (their disproportionation can practically be ignored [43]). The scheme of these reactions is presented in [35].
The rate equation for ethanediol formation by the chain mechanism in reaction 3 and by the nonchain mechanism in reactions 4 and 5 in the methanol-formaldehyde system has a complicated form3 as compared to Eq. (1) for the formation rate of the other 1,2-alkanediols [12]:
If the rate of ethanediol formation by the dimerization mechanism in reaction 5 is ignored for the reason that it is small as compared to the total rate of ethanediol formation in reactions 3 and 4, Eq. (9) will be identical to Eq. (5). After the numerator and denominator on the right-hand side of Eq. (5) are divided by k-2 ≡ k3a, one can replace K2 in this equation with K2 = K2/k-2, which is the equilibrium constant for the reverse of reaction 2. Ignoring the reverse of reaction 2 ( k3a = 0, β = 0) makes Eq. (5) identical to Eq. (4) for Scheme 1 at k3b = 0 (see the Section 2.1). In this case, the rate constant K2 is effec-tive.
Addition to Oxygen
The addition of a free radical or an atom to one of the two multiply bonded atoms of the oxygen molecule yields a per-oxyl free radical and thus initiates oxidation, which is the basic process of chemical evolution. The peroxyl free radical then abstracts the most labile atom from a molecule of the com-pound being oxidized or decomposes to turn into a molecule of an oxidation product. The only reaction that can compete with these two reactions at the chain evolution stage is the addition of the peroxyl radical to the oxygen molecule (provided that the oxygen concentration is sufficiently high). This reaction yields a secondary, tetraoxyalkyl, 1:2 adduct radical, which is the heaviest and the largest among the reactants. It is less reactive than the primary, 1:1 peroxyl adduct radical and, as aconsequence, does not participate in further chain propagation. At moderate temperatures, the reaction proceeds via a non-branched-chain mechanism.
Addition of Hydrocarbon Free Radicals
Usually, the convex curve of the hydrocarbon (RH) autooxidation rate as a function of the partial pressure of oxygen ascends up to some limit and then flattens out [6]. When this is the case, the oxidation kinetics is satisfactorily describable in terms of the conventional reaction scheme [2,5,6,16,44,45], which involves two types of free radicals. These are the hy-drocarbon radical R• (addend radical) and the addition product (1:1 adduct radical). However, the existing mechanisms are inapplicable to the cases in which the rate of initiated ox-idation as a function of the oxygen concentration has a maximum (Figures 4 & 5) [46,47]. Such dependences can be described in terms of the competition kinetics of free-radical chain ad-dition, whose reaction scheme involves not only the above two types of free radicals, but also the radical (1:2 adduct) inhibiting the chain process [13,14].
Figure 4: (1, ) Reconstruction of the functional dependence of the 2-methylbenzyl hydroperoxide formation rate V3(R O2H) on the dissolved oxygen concentration x from empirical data (points) using Eq. (3a) (model optimization with respect to the parameter α) for the o-xylene–oxygen system at 373K [46] (standard deviation of SY = 5.37 10–7. (2, □) Reconstruction of the functional dependence of the total hydrogen peroxide formation rate V3, 7(Н2О2) on the dissolved oxygen concentration x from empirical data (symbols) using Eqs. (3a) and (14a) with β = 0 (model optimization with respect to the parameter α) for the γ-radiolysis of water saturated with hy-drogen and containing different amounts of oxygen at 296 K [63] (SY = 1.13 10–8). The dashed curve described V3(H2 O2) as a function of the oxygen concentration x based on Eq. (3a) (model optimization with respect to α) and the experimental data of curve 2 (SY = 1.73 10–8).
Scheme 3:
Chain propagation
Inhibition
Chain Termination
The only difference between the kinetic model of oxidation represented by Scheme 3 and the kinetic model of the chain addition of 1-hydroxyalkyl radicals to the free (unsolvated) form of formaldehyde in nonmethanolic alco-hol-formaldehyde systems [8,9] (Scheme 2, Section 3.1) is that in the former does not include the formation of the mo-lecular 1:1 adduct via reaction 4.
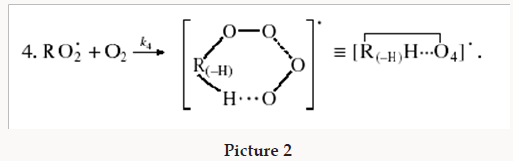
The decomposition of the initiator I in reaction 1 yields a reactive radical 0 R• , which turns into the ultimate product R0H via reaction 1a, generating an alkyl radical R•, which participates in chain propagation. In reaction 2, the addition of the free radical R• to the oxygen molecule yields a reactive alkylperoxyl 1:1 adduct radical 2 RO• [45], which possesses increased energy owing to the energy released upon the con-version of the O=O bond into the ordinary bond RО-О• (for addition in the gas phase under standard conditions, this energy is 115-130 kJ mol-1 for C1-C4 alkyl radicals [1,2,4] and 73 kJmol-1 for the allyl radical [4]). Because of this, the ad-duct radical can decompose (reaction 3a) or react with some neighbor molecule (reaction 3 or 4) on the spot, without dif-fusing in the solution and, accordingly, without entering into any chain termination reaction. In reaction 3, the interaction between the radical adduct 2 RO• and the hydrocarbon mole-cule RH yields, via a chain mechanism, the alkyl hydroper-oxide R O2H (this reaction regenerates the chain carrier R• and, under certain conditions, can be viewed as being reversible [2]) or the alcohol ROH (this is followed by the regeneration of R• via reaction 3b). The latter (alternative) pathway of reaction 3 consists of four steps, namely, the breaking of old bonds and the formation of two new bonds in the reacting structures. In reaction 3a, the isomerization and decomposition of the al-kylperoxyl radical adduct with O-O and C-O or C-H bond breaking take place [6,44], yielding the carbonyl com-pound R′(-Н)НО or R(-2Н)НО. Reaction 3b produces the alcohol R′¢OH or water and regenerates the free radical R• (here, R′ and R′′ are radicals having a smaller number of carbon atoms than R). As follows from the above scheme of the process, consecutive reactions 3a and 3b (whose rates are equal within the quasisteady- state treatment), in which the highly reactive fragment, oxyl radical R′′О• (or •ОН) forms and then disap-pears, respectively, can be represented as a single, combined bimolecular reaction 3a,b occurring in a “cage” of solvent molecules. Likewise, the alternative (parenthesized) pathways of reactions 3 and 3b, which involve the alkoxyl radical RО•, can formally be treated as having equal rates. For simple alkyl C1-C4 radicals R, the pathway of reaction 3 leading to the alkyl hydroperoxide R O2H is endothermic ( ΔÍ•298 = 30-80kJ mol-1) and the alternative pathway yielding the alcohol ROH is exothermic (= ΔÍ•298 -120 to -190kJ mol-1), while the parallel reaction 3a, which yields a carbonyl compound and the alkoxyl radical R′′О• or the hydroxyl radical •ОН, is exothermic in both cases (ΔÍ 2•98 = -80 to -130kJ mol-1), as also is reaction 3b ( ΔÍ•298 = -10 to -120kJmol-1), consecutive to reaction 3a, according to thermo chemical data for the gas phase [2-4]. In reaction 4, which is competing with (parallel to) reactions 3 and 3a (chain propagation through the reactive radical R•), the resulting low-reactive radical that does not participate in further chain propagation and inhibits the chain process is supposed to be the alkyltetraoxyl 1:2 radical adduct4,5 4 RO• , which has the largest weight and size. This radical is possibly stabilized by a weak intramolecular H···O hydrogen bond [54] shaping it into a sixmembered cyclic structure 6 (sev-en-membered cyclic structure in the case of aromatic and certain branched acyclic hydrocarbons) [56,57]: (Picture 2)
Reaction 4 in the case of the methylperoxyl radical 3 2 CH O• adding to the oxygen molecule to yield the methyltetraoxyl radical 3 4 CH O• takes place in the gas phase, with heat ab-sorption equal to 110.0±18.6kJ mol-1 [49] (without the energy of the possible formation of a hydrogen bond taken into account). The exothermic reactions 6 and 7, in which the radical R• or 4 RO• undergoes disproportionation, include the isomerization and decomposition of the radical7. The latter process is likely accompanied by chemiluminescence typical of hydrocarbon oxidation [52]. These reactions regen-erate oxygen as O2 molecules (including singlet oxygen8 [52,59]) and, partially, as O3 molecules and yield the carbonyl compound R(-2H)HO (possibly in the triplet excited state [52]). Depending on the decomposition pathway, the other possible products are the alcohol ROH, the ether ROR, and the alkylperoxide R O2R. It is likely that the isomerization 4 RO• and decomposition of the radical via reactions 6 and 7 can take place through the breaking of a C-C bond to yield carbonyl compounds, alcohols, ethers, and organic peroxides containing fewer carbon atoms than the initial hydrocarbon, as in the case of the alkylperoxyl radical 2 RO• in reaction 3a. At later stages of oxidation and at sufficiently high temperatures, the resulting aldehydes can be further oxidized into respective carboxylic acids. They can also react with molecular oxygen so that a C-H bond in the aldehyde molecule breaks to yield two free radicals ( 2 HO• and •R′(-H)O or •R(-2H)O). This process, like possible ozone decomposition yielding an •O• atom or peroxide decomposition with O-O bond breaking, leads to degenerate chain branching [6]. The equations describing the formation rates of molecular products at the chain propagation and termination stages of the above reaction scheme, set up using the quasi-steady-state treatment, appear as follows:
where V1 is the initiation rate, l = [RH] and x = [
O2] are the
molar concentrations of the starting components (l >> x), α =
k3/
k4 and β =
k3a/
k4 (mol dm-3) are the ratios of the rate constants
of the competing (parallel) reactions,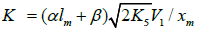 is the rate constant of the addition of the alkyl radical R• to the
oxygen molecule (reaction 2) as determined by solving the
quadratic equation following from the rate function extremum
condition ∂V3,3a/∂x=0, lm and xm are the values of l and x at the
maximum point of the function
is the rate constant of the addition of the alkyl radical R• to the
oxygen molecule (reaction 2) as determined by solving the
quadratic equation following from the rate function extremum
condition ∂V3,3a/∂x=0, lm and xm are the values of l and x at the
maximum point of the function 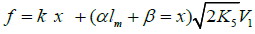 and
and
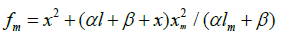
The ratios of the rates of the competing reactions are V3/V4 = αl/x and V3a/V4 = β/x, and the chain length is ν = (V3 + V3a)/V1. Eq. (11) is identical to Eq. (6). Eqs (10a) and (10a) were ob-tained by replacing the rate constant K2 in Eqs. (10) and (11) with its analytical expression (for reducing the number of unknown parameters to be determined directly).
For αl >> β ( V3 >> V3a), when the total yield of alkyl hydroperoxides and alcohols having the same number of carbon atoms as the initial compound far exceeds the yield of carbonyl compounds, as in the case of the oxidation of some hydro-carbons, the parameter β in Eqs. (10) and (10a) can be ne-glected (β = 0) and these equations become identical to Eqs. (3) and (3a) with the corresponding analytical expression for K2.
In the alternative kinetic model of oxidation, whose chain termination stage involves, in place of R• (Scheme 3), 2 RO• radicals reacting with one another and with 4 RO• radicals, the dependences of the chain formation rates of the products on the oxygen concentration x derived by the same method have no maximum:
In the kinetic model of oxidation that does not include the
competing reaction 4 (
k4 = 0) and involves the adicals R• and 2 RO•
(the latter instead of 4 RO• in Scheme 3) in reactions 5-7, the reaction
rate functions
V3 and
V3a obtained in the same way are fractional
rational functions in the form of a0x/(b0x + c0), where a0, b0, and c0
are coefficients having no extremum. For a similar kinetic model in which reactions 3a,b and 4 appearing in the above scheme
are missing (
k3a=
k4=0), Walling [5], using the quasi- steady-state
treatment in the long kinetic chain approximation, when it can be
assumed that V2 =
V3, without using the substitution 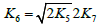 [5,6,16] (as distinct from this work), found that V2 =
V3 is an
irrational function of x:
[5,6,16] (as distinct from this work), found that V2 =
V3 is an
irrational function of x: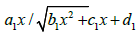 where a1, b1, C1, and d1 are
coefficients. Again, this function has no maximum with respect to
the concentration of any of the two components.
where a1, b1, C1, and d1 are
coefficients. Again, this function has no maximum with respect to
the concentration of any of the two components.
Thus, of the three kinetic models of oxidation mathematically analyzed above, which involve the radicals R• and 2 RO• in three types of quadratic-law chain termination reactions (reactions 5-7) and are variants of the conventional model [2,5,6,16,44,45], the last two lead to an oxidation rate versus oxygen concentration curve that emanates from the origin of coordinates, is convex upward, and has an asymptote parallel to the abscissa axis. Such monotonic dependences are observed when the oxygen solubility in the liquid is limited under given experimental conditions and the oxygen concentration attained9 is [ O2]top≤xm.
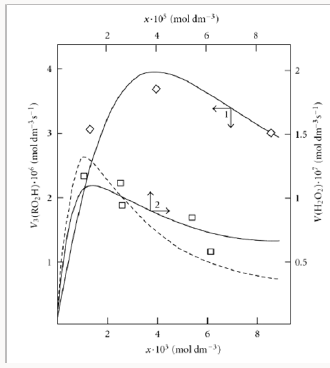
Figure 5: (1, 2) Quantum yields of (1, ●) hydrogen peroxide and (2, ○) water resulting from the photochemical oxidation of hydrogen in the hydro-gen–oxygen system as a function of the oxygen concentration x (light wave-length of 171.9– 172.5nm, total pressure of 105Pa, room temperature [64]). (3, 4) Hydrogen peroxide formation rate V(Н2О2) (dashed curves) as a function of the rate V(О2) at which molecular oxygen is passed through a gas-discharge tube filled with (3, ) atomic and (4, □) molecular hydrogen. Atomic hydrogen was obtained from molecular hydrogen in the gasdischarge tube before the measurements (total pressure of 25–77Pa, temperature of 77K [47]). The symbols represent experimental data.
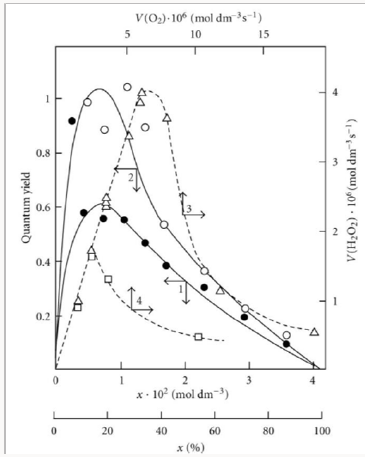
Unlike the conventional model, the above kinetic model of freeradical nonbranched-chain oxidation, which includes the pairs of competing reactions 3-4 and 3a-4 (Scheme 3), allows us to describe the non monotonic (peaking) dependence of the oxidation rate on the oxygen concentration (Figure 4). In this oxidation model, as the oxygen concentration in the binary system is increased, oxygen begins to act as an oxidation auto inhibitor or an antioxidant via the further oxidation of the alkylperoxyl 1:1 adduct radical 2 RO• into the low-reactive 1:2 adduct radical 4 RO• (reactions 4 and 6 lead to inefficient consumption of the free radicals 2 RO• and R• and cause shortening of the kinetic chains). The optimum oxygen concentration xm, at which the oxidation rate is the highest, can be calculated using kinetic equations (10a) and (11a) and Eq. (3a) with β = 0 or the corresponding analytical expression for K2. In the familiar monograph Chain Reactions by Semenov [60], it is noted that raising the oxygen concentration when it is al-ready sufficient usually slows down the oxidation process by shortening the chains. The existence of the upper (second) ignition limit in oxidation is due to chain termination in the bulk through triple collisions between an active species of the chain reaction and two oxygen molecules (at sufficiently high oxygen partial pressures). In the gas phase at atmospheric pressure, the number of triple collisions is roughly estimated to be 103 times smaller than the number of binary collisions (and the probability of a reaction taking place depends on the specificity of the action of the third particle) [60]. Note that in the case of a gas-phase oxidation of hydrogen at low pressures of 25-77 Pа and a temperature of 77 К [47] when triple collisions are unlikely, the dependence of the rate of hydrogen peroxide formation on oxygen concentration (the rate of passing of molecular oxygen via the reaction tube) also has a pronounced maximum (see curves 3 and 4 in Figure 5) that in-dicates a chemical mechanism providing the appearance of a maximum (see reaction 4 of Scheme 4).
Curve 1 in Figure 4 illustrates the fit between Eq. (3a) at αl >> β and experimental data for the radiation-induced oxidation of o-xylene in the liquid phase at 373K in the case of 2-methylbenzyl hydroperoxide forming much more rapidly than o-tolualdehyde ( V3>> V3a and αl >> β) [46]. The oxygen concentration limit in oxylene is reached at an oxygen concentration of [ O2]top > xm, which corresponds to the third ex-perimental point [46]. The oxygen concentration was calcu-lated from the oxygen solubility in liquid xylene at 373K [61]. The following quantities were used in this mathematical description: 60Co γ-radiation dose rate of P = 2.18Gy s-1 and total initiation yield of G(o-СН3С6Н4ĊН2) = 2.6 particles per 100 eV of the energy absorbed by the solution [46]; V1 = 4.73 × 10-7 mol dm-3 s-1, and 2k5 = 1.15 × 1010 dm3 mol-1 s-1. The resulting value of the parameter α is (9.0±1.8) × 10-3; hence, K2 = (3.2±0.8)´105 dm3 mol-1 s-1. From the data presented in [62], it was estimated that k4 = k3/α = (5.2 ± 1.2) × 102 dm3 mol-1 s-1.
Addition of the Hydrogen Atom
A number of experimental findings concerning the autoinhibiting effect of an increasing oxygen concentration at modest temperatures on hydrogen oxidation both in the liquid phase [63] (Figure 4, curve 2) and in the gas phase [47,64,65] (Figure 5), considered in our earlier work [13, 56, 57, 66], can also be explained in terms of the competition kinetics of free radical addition [14,67]. From Figure 5 shows that the quantum yields of hydrogen peroxide and water (of products of photochemical oxidation of hydrogen at atmospheric pressure and room temperature) are maximum in the region of small concentrations of oxygen in the hydrogen-oxygen system (curves 1 and 2, respectively) [64].
Scheme 4
Nonbranched-chain oxidation of hydrogen and changes in enthalpy (ΔÍ 2•98 , kJ mol-1) for elementary reactions10
Scheme 4:
Chain propagation
Inhibition
Chain termination
The hydroperoxyl free radical [75-78] resulting from reaction 2 possesses an increased energy due to the energy released the conversion of the О=О multiple bond into the НО-О• ordinary bond. Therefore, before its possible decomposition, it can interact with a hydrogen or oxygen molecule as the third body via parallel (competing) reactions 3 and 4, respectively. The hydroxyl radical НО• that appears and disap-pears in consecutive parallel reactions 3 (first variant) and 3′ possesses additional energy owing to the exothermicity of the first variant of reaction 3, whose heat is distributed between the two products. As a consequence, this radical has a sufficiently high reactivity not to accumulate in the system during these reactions, whose rates are equal ( V3 = V3′) under quasi- steady-state conditions, according to the above scheme. Parallel reactions 3 (second, parenthesized variant) and 3′ regenerate hydrogen atoms. It is assumed [56,57] that the hydrotetraoxyl radical (first reported in [79,80]) re-sulting from endothermic reaction 4, which is responsible for the peak in the experimental rate curve (Figure 4, curve 2), is closed into a five-membered [Î Î ─Í Î Î ]• cycle due to weak intramolecular hydrogen bonding [54,81]. This structure imparts additional stability to this radical and makes it least reactive.
The 4 HO• radical was discovered by Staehelin et al. [82] in a pulsed radiolysis study of ozone degradation in water; its UV spectrum with an absorption maximum at 260nm 2 1 4 280 ( ) 320 15 nm ε HO• = ± m mol− was reported. The spectrum of the 4 HO• radical is similar to that of ozone, but the molar absorption coefficient 4 max ε (HO• )λ of the former is almost two times larger [82]. The assumption about the cyclic structure of the 4 HO• radical can stem from the fact that its mean lifetime in water at 294K, which is (3.6±0.4) × 10-5 s (as estimated [66] from the value of 1/k for the reaction 4 2 2HO• k→HO•+ O [82] is 3.9 times longer than that of the linear 3 HO• radical [68, 83] estimated in the same way [66] for the same conditions [84], (9.1±0.9)×10-6 s. MP2/6-311++G** calculations using the Gaussian-98 program confirmed that the cyclic structure of 4 HO• [85] is energetically more favorable than the helical structure [68] (the difference in energy is 4.8-7.3kJmol-1, depending on the computational method and the basis set)11. For example, with the MP2(full)/6-31G(d) method, the difference between the full energies of the cyclic and acyclic 4 HO• conformers with their zero-point energies (ZPE) values taken into account (which reduces the energy difference by 1.1kJ mol-1) is -5.1kJmol-1 and the entropy of the acyclic-to-cyclic 4 HO• transition is –1 – 98 1 2 ΔS = −1.6 kJ mol K . Therefore, under standard conditions, 4 HO• can exist in both forms, but the cyclic structure is obviously dominant (87%, Keq = 6.5) [85].
Reaction 4 and, to a much lesser degree, reaction 6 inhibit the chain process, because they lead to inefficient consumption of its main participants 2 −HO• and Н•.
The hydrogen molecule that results from reaction 5 in the gas bulk possesses an excess energy, and, to acquire stability within the approximation used in this work, it should have time for deactivation via collision with a particle M capable of accepting the excess energy [87]. To simplify the form of the kinetic equations, it was assumed that the rate of the bimo-lecular deactivation of the molecule substantially exceeds the rate of its monomolecular decomposition, which is the reverse of reaction 5 [2].
Reactions 6 and 7 (taking into account the principle of detailed balance for the various pathways) regenerate hydrogen and oxygen (in the form of 3 2 ( ) g Î X −Σ− molecules, including the singlet states with 1 1 298 2 ( , ) 94.3 f g ΔH o a Δ = kjmol− [49, 70] and 1 1 298 2 ( , ) 161.4 f g ΔH o B Σ− = kjmol− [70] which are deactivated by collisions, and in the form of O3) and yield hydrogen peroxide or water via a nonchain mechanism, presumably through the intermediate formation of the unstable hydrogen tetraoxide molecule H2O4 [88] 12. Ozone does not interact with molecular hydrogen. At moderate temperatures, it decomposes fairly slowly, particularly in the presence of 3 Î 2 (X Σ−g ) [70]. The reaction of ozone with Н• atoms, which is not impossible, results in their replacement with НО• radicals. The relative contributions from reactions 6 and 7 to the process kinetics can be roughly estimated from the corresponding enthalpy increments (Scheme 4).
When there is no excess hydrogen in the hydrogen-oxygen system and the homomolecular dimer O4 [71-74,89,90], which exists at low concentrations (depending on the pressure and temperature) in equilibrium with O2 [70], can directly capture the Н• atom to yield the heteronuclear cluster 4 HO• ,13 which is more stable than O2 [70] and cannot abstract a hydrogen atom from the hydrogen molecule, nonchain hydrogen oxida-tion will occur to give molecular oxidation products via the disproportionation of free radicals.
The low-reactive hydrotetraoxyl radical 4 HO• [82], which presumably has a high-energy density [71], may be an intermediate in the efficient absorption and conversion of biolog-ically hazardous UV radiation energy the Earth upper atmos-phere. The potential energy surface for the atmospheric reac-tion 3 HO• +O in which the adduct 2 4HO• ( A) was considered as an intermediate, was calculated by the DMBE method [91]. From this standpoint, the following reactions are possible in the upper troposphere, as well as in the lower and middle stratosphere, where most of the ozone layer is situated (altitude of 16-30 km, temperature of 217-227K, pressure of 1.0 × 104-1.2 × 103 Pa [92]; the corresponding 298 ΔH reaction values are given in kJ mol-1 [49]):
The 4 HO• radical can disappear via disproportionation with a molecule, free radical, or atom in addition to dissocia-tion. Note that emission from 1 2( )g O aΔ and 1 2 ( ) g Î b Σ+ is observed at altitudes of 30-80 and 40-130km, respectively [93]. Staehelin et al. [82] pointed out that, in natural systems in which the concentrations of intermediates are often very low, kinetic chains in chain reactions can be very long in the ab-sence of scavengers since the rates of the chain termination reactions decrease with decreasing concentrations of the in-termediates according to a quadratic law, whereas the rates of the chain propagation reactions decrease according to a linear law.
The kinetic description of the noncatalytic oxidation of hy-drogen, including in an inert medium [87], in terms of the simplified scheme of free-radical non branched-chain reactions (Scheme 4), which considers only quadratic-law chain termi-nation and ignores the surface effects [47], at moderate tem-peratures and pressures, in the absence of transitions to un-steady-state critical regimes, and at a substantial excess of the hydrogen concentration over the oxygen concentration was obtained by means of quasisteady- state treatment, as in the previous studies on the kinetics of the branched-chain free-radical oxidation of hydrogen [76], even though the ap-plicability of this method in the latter case under unsteady states conditions was insufficiently substantiated. The method was used with the following condition:14 6 5 7 K = 2K 2K (see Introduction). The equation for the rate of the chain formation of hydrogen peroxide and water, 3 2 2 2 3 2 V (H O ; H O) =V (H O) , via reactions 3 and 3′ is identical to Eq. (3, 3a) with the cor-responding analytical expression for K2. The ratio of the rates of the competing reactions is V3/V4 = αl/x, and the chain length is ν = V3/V1. The rates of nonchain formation of hydrogen peroxide and water via reactions (6) and (7) quadratic-law chain termination are identical to Eqs. (13) and (14) provided that β = 0. In these equations, l and x are the molar concentra-tions of hydrogen and oxygen (l >> x), lm and xm are the re-spective concentrations at the maximum point of the function, V1 is the rate of initiation (reaction 1), α = k3/ k4, the rate con-stant 2 2 5 1 2 / m m K =αl K V x is derived from the condition ∂ V3/∂x = 0, and 2k5 is the rate constant of reaction 5 (hydrogen atom recombination), which is considered as bimolecular within the given approximation.15
In the case of nonchain hydrogen oxidation via the above
addition reaction
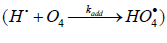
the formation rates of the molecular oxidation products in reactions 6 and 7 (Scheme 4, K2 = k3 = k4 = 0) are defined by modified Eqs. (13) and (14) in which β = 0, (αl + x) is replaced with 1, and K2 is replaced with kaddKeq (kaddKeq is the effective rate constant of Н• addition to the О4 dimer, Кeq = k/k′ is the equilibrium con-stant of the reversible reaction 2 4 2O ⇔O with k′ >> kadd[Н•]). The formation rates of the stable products of non-chain oxidation ( k3 = 0), provided that either reactions (2) and (4) or reaction (2) alone ( k4 = 0) occurs (Scheme 4; in the latter case, reactions 6 and 7 involve the 2 HO• radical rather than 4 HO• ), are given by modified Eqs. (13) and (14) with β = 0, (αl + x) replaced with 1, and х2 replaced with х.
Note that, if in Scheme 4 chain initiation via reaction 1 is due to the interaction between molecular hydrogen and molecular oxygen yielding the hydroxyl radical НО• instead of Н• atoms and if this radical reacts with an oxygen molecule (reaction 4) to form the hydrotrioxyl radical 3 HO• (which was obtained in the gas phase by neutralization reionization (NR) mass spectrometry [83] and has a lifetime of >10-6 s at 298K) and chain termination takes place via reactions 5-7 involving the HO• and 3 HO• radicals instead of HO• and 4 HO• respectively, the expressions for the water chain formation rates derived in the same way will appear as a rational function of the oxygen concentration x without a maximum: V3 (H2O) =V1 k3l / ( k4x + 2k5V1) .
Curve 2 in Figure 4 describes, in terms of the overall equation 3 2 3,7 1 ( ) / m m V =V x αlf + x f for the rates of reactions 3 and 7 (which was derived from Eqs. 3a and 14, respectively, the latter in the form of 4 2 7 1 / m V =V x f (14a) [96] in which K2 is replaced with its analytical expression derived from Eq. (10) with β = 0 everywhere), the dependence of the hydrogen peroxide formation rate (minus the rate 2 2 5.19 10 8 3 1 H O V = × − moldm− s− of the primary formation of hydrogen peroxide after completion of the reactions in spurs) on the concentration of dissolved oxygen during the γ-radiolysis of water saturated with hydrogen (at the initial concentration 7×10−4moldm−3 ) at 296K [63]. These data were calculated in the present work from the initial slopes of hydrogen peroxide buildup versus dose curves for a 60Co γ-radiation dose rate of Р = 0.67Gy s-1 and absorbed doses of D ≅ 22.5-304.0 Gy. The following values of the primary radiation-chemical yield G (species per 100 eV of energy absorbed) for water γ-radiolysis products in the bulk of solution at pH 4-9 and room temperature were used (taking into account that V = GP and V1 = GHP): 2 2 0.75 H O G = and 0.6 H G = (initiation yield; see below) [94]; V1 = 4.15 × 10-8mol dm-3 s-1; 2k5 = 2.0 × 1010 dm3 mol-1 s-1 [94]. As can be seen from Figure 4, the best description of the data with an in-crease in the oxygen concentration in water is attained when the rate V7 of the formation of hydrogen peroxide via the non chain mechanism in the chain termination reaction 7 (curve 1, α = (8.5±2) × 10-2) is taken into account in addition to the rate V3 of the chain formation of this product via the propagation reaction 3 (dashed curve 2, α = 0.11±0.026). The rate constant of addition reaction 2 determined from α is substantially underestimated: K2 = 1.34 × 107 (vs. 2.0 × 1010 [94]) dm3 mol-1 s-1. The difference can be due to the fact that the radiation chemical specifics of the process were not considered in the kinetic description of the experimental data. These include oxygen consumption via reactions that are not involved in the hydrogen oxidation scheme [66,97,98] and reverse reactions resulting in the decomposition of hydrogen peroxide by intermediate products of water radiolysis ( aq e− , Н•, НО•), with the major role played by the hydrated electron [94].
General Scheme of the Addition of Free Radicals to Molecules of Alkenes, Formaldehyde, and Oxygen
The general scheme of the non branched-chain addition of a free radical from a saturated compound to an alkene (and its functionalized derivative), formaldehyde, or dioxygen (which can add an unsaturated radical as well) in liquid homogeneous binary systems of these components includes the following reactions [57,97,98].
Scheme 5
for addition to an alkeneat comparable component concen-trations,Initiation
Chain propagation
for addition to О2and the 1-hydroxyalkyl radical to СН2О,
Inhibition
For addition to an alkeneor СН2О,
for addition to О2,
Chain termination
In this scheme, I is the initiator, for example, a peroxide [5,17,18,29,30]; 0 R• is any reactive radical (initiator); A is an atom of hydrogen [2,5,6,17,18,22-24,29-32] or halogen [2,5,19-21]; B is an atom of hydrogen [5,17-21,23,24, 29-32], halogen [22], or oxygen (in oxidation) [2,5 6,16,44-46]; 1 R• is a radical such as •PCl2 [19], •CCl3 [20], an alkyl [2,5,6,21], a 1-hydroxyalkyl [5,6,17,22-24,29,32], or a similar functional ized radical [5] (addend); 2 R• is the formyl 8,9,29], an alkenyl (propenyl or higher) [2 5,17-22], a 1-hydroxyalkenyl [5,17,18,23,24], or a similar functionalized low-reacrtive rad-ical [5,18] (inhbitor) or the oxygen atom (in oxidation) [2,5,6,13,14,16, 44-46,56,57, 96-98]; 2a R• is the low-reactive alkyltetraoxyl 1:2 adduct radical 4 R• [13,14,56,57,96-98] (inhibitor); 3 R• is the active 1:1 adduct radical; 4 R• is an active fragment radical, such as hydroxymethyl [8,9,12,29,32], an alkoxyl radical, or hydroxyl (in oxidation) [2,5,6,13,14,16,44,46,56,57,96-98]; R0A, R0B, R1A, and R4A are saturated molecules; R2B is an unsaturated molecule, viz., an alkene [2,5,11,17-22], formaldehyde [8,9,12,29-32], or dioxygen (in oxidation) [2,5,6,13,14,16,44-46,56,57,96-98]; R¢R′′CO is a carbonyl compound viz., aldehyde [2,6,8,9,12,14,29-32,44] or ketone [2,6,14,29,32,44]; R3A and R3B are molecular products (1:1 adducts); and Prod stands for molecular products of the dimerization and disproportionation of free radicals.
The chain evolution stage of Scheme 5 includes consecutive reactions 2, 3; 2, 3a; and 3a, 3b; parallel (competitive) reactions 3, 3a; 3, 3b; 3, 4 (or 4a); and 3a, 4 (or 4a); and consecutive- parallel reactions 2 and 4 (or 4a). Addition to alkenes is described by reactions 1-3, 4, and 5-7 and the corresponding rate equations (1)- (4a). Addition to the carbonyl carbon atom of the free (unsolvated) form of formaldehyde is represented by reactions 1, 1a, 2-4 (the main products are a 1,2-alkanediol, a carbonyl compound, and methanol), and 5-7 and is described by Eqs. (5) and (6). In the case of hydroxymethyl addition, the process includes reactions 1, 1a, 2, 3, 5a, 4 (the main product is ethanediol), and 5-7 and is described by Eq. (9). If the nonchain formation of ethanediol in reaction 5 is ignored, the process is described by Eq. (5). Addition to the oxygen molecule is described by reactions 1, 1a, 2-3b, 4a (the main products are an alkyl hydroperoxide, alcohols, carbonyl compounds, and water), and 5-7 and Eqs. (10) and (11).
The main molecular products of the chain process - R3А, R¢R′′СО, and R4А - result from reactions 3, 3a, and 3b - chain propagation through the reactive free radical 1 R• or 4 R• , R¢R′′CO. The competing reaction 4, which opposes this chain propagation, yields the byproduct R3B a nonchain mechanism. The rate of formation of the products is a complicated function of the formation rates ( V3a = V3b) and disappearance rates of the free radicals
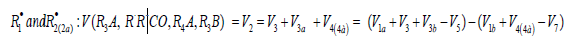
The rates of reactions 5-7 at k11 = 0 ([R1A] >> [R2B]) are given by Eqs. (12)-(14). The rate ratios of the competing reactions are V3/V4(4а) = αl/x and V3а/V4(4а) = β/x (where α = k3/ k4(4а), β = k3а/ k4(4а) mol dm-3, and l and x are the molar concentrations of the reactants R1A and R2B, respectively), and the chain length is ( ) 3 3 1 / a v = V +V V . Unlike the dependences of the rates of reactions 4a (or 4 at k11 = 0, with V4(4a) ≤ V1), 5, and 7 (for the last two - Eqs. (12) and (14)), the dependences of the rates V of reactions 3, 3a,b, 4 (at k11 ≠ 0), and 6 (Eqs. (1), (3)-(6), (10), (11), and (13)) on x have a maximum. Reaction 1b, which competes with reaction 1a, gives rise to a maximum in the dependence described by Eq. (2), whereas reaction 4 or 4a, competing with reactions 3 and 3a,b, is responsible for the maxima in the dependences defined by Eqs. (1), (3)-(6) or (10) and (11). The low-reactive radicals 16 2 R• and 2a R• , resulting from reactions 4 and 4a, inhibit the non branched-chain addition of two alkenes (or formaldehyde) and dioxygen, re-spectively. Reaction 4a leads to non-productive loss of 3 R• adduct radicals.
For approximate estimation of the parameters of the kinetic
equations (3), (4), (10), and (11), Eq. (4) under the conditions (a)
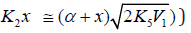 (ascending branch of a peaked curve) and
(ascending branch of a peaked curve) and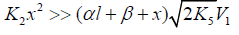 (descending branch) is transformed
into simple functions (direct and inverse propor-tionality,
respectively) of the concentration x of the unsaturated compound.
These functions allow tentative estimates of the parameters K2 and
α to be derived from the experimental product formation rate V
provided that V1 and 2k5 are known:
(descending branch) is transformed
into simple functions (direct and inverse propor-tionality,
respectively) of the concentration x of the unsaturated compound.
These functions allow tentative estimates of the parameters K2 and
α to be derived from the experimental product formation rate V
provided that V1 and 2k5 are known:
where ϕ = 1 under conditions (a) and (b) and ϕ = 2 at the point
of maximum (where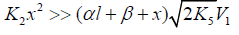 Equations (10) and
(11) under the condition
Equations (10) and
(11) under the condition 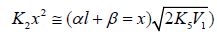 (descending
branch of a peaked curve) can be transformed into Eqs. (17) and
(18), respectively, which express the simple, inversely proportional
dependences of reaction rates on x and provide tentative estimates
of α and β:
(descending
branch of a peaked curve) can be transformed into Eqs. (17) and
(18), respectively, which express the simple, inversely proportional
dependences of reaction rates on x and provide tentative estimates
of α and β:
where ϕ = 2 at the point of maximum (where 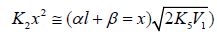 and ϕ = 1 for the descending branch of
the curve. Equation (3) for
V3, 4 under condition (b) transforms into
Eq. (17). For radiation-chemical processes, the rates V in the kinetic
equations should be replaced with radiation-chemical yields G
using the necessary unit conversion factors and the relation-ships V
= GP and 1 V1 =ε1G(R• )P ,where P is the dose rate, e1 is the electron
fraction of the saturated component R1A in the reaction system
[100], and 1 G(R• ) is the initial yield of the chain-carrier free radicals
(addends) - initiation yield [39,94].
and ϕ = 1 for the descending branch of
the curve. Equation (3) for
V3, 4 under condition (b) transforms into
Eq. (17). For radiation-chemical processes, the rates V in the kinetic
equations should be replaced with radiation-chemical yields G
using the necessary unit conversion factors and the relation-ships V
= GP and 1 V1 =ε1G(R• )P ,where P is the dose rate, e1 is the electron
fraction of the saturated component R1A in the reaction system
[100], and 1 G(R• ) is the initial yield of the chain-carrier free radicals
(addends) - initiation yield [39,94].
Conclusion
In summary, the material on the kinetics of non-branchedchain addition of free saturated radicals to multiple bonds of alkene (and its derivative), formaldehyde, or oxygen molecules makes it possible to describe, using rate equations (1)-(6), (9)-(11) obtained by quasi-steady-state treatment, experimental dependences with a maximum of the formationrates of molecular 1:1 adducts on the concentration of an un-saturated compound over the entire region of its change in binary reaction systems consisting of saturated and unsatu-rated components (Figures 1, 3, 4).
The proposed addition mechanism involves the reaction of a free 1:1 adduct radical with an unsaturated molecule yielding a low-reactive free radical (the reaction 4 competing with the chain propagation reactions in Schemes 1-5). In such reaction systems, the unsaturated compound is both a reactant and an autoinhibitor, specifically, a source of low-reactive free radi-cals shortening kinetic chains. The progressive inhibition of the nonbranchedchain processes, which takes place as the concentration of the unsaturated compound is raised (after the maximum process rate is reached), can be an element of the self-regulation of the natural processes that returns them to the stable steady state
A similar description is applicable to the nonbranched-chain free-radical hydrogen oxidation in water at 296K [63] (Figure 4, curve 2). Using the hydrogen oxidation mechanism considered here, it has been demonstrated that, in the Earth’s upper at-mosphere, the decomposition of O3 in its reaction with the НО• radical can occur via the addition of the latter to the ozone molecule, yielding the radical 4 HO• , which is capable of ef-ficiently absorbing UV radiation [82].
The optimum concentration xm of unsaturated component in the binary system at which the process rate is maximal can be derived with the help of obtained kinetic equations (3a), (4a), (10a), and (11a) or from the corresponding analytical expres-sions for K2 if other parameters are known. This opens a way to intensification of some technological processes that are based on the addition of free radicals to the double bonds of un-saturated molecules and occur via a nonbranched-chain mechanism through the formation of 1:1 adducts.
References
- LV Gurvich, GV Karachevtsev, VN Kondrat’ev, YuA Lebedev, VA Medvedev, et al. (1974) Bond Dissociation Energies, Ionization Potentials, and Electron Affinity, VN Kondrat’ev, Editor, Nauka, Moscow.
- SW Benson (1976) Thermo chemical Kinetics: Methods for the Estimation of Thermo chemical Data and Rate Parameters, (2nd edn), Wiley, New York, USA.
- JB Pedley, RD Naylor, SP Kirby (1986) Thermo chemical Data of Organic Compounds, (2nd Ed), Chapman & Hall, London.
- YuD Orlov, YuA Lebedev, ISh Saifullin (2001) Thermochemistry of Organic Free Radicals, AM Kutepov, Editor, Nauka, Moscow.
- Ch Walling (1958) Free Radicals in Solution, Wiley, New York, USA.
- NM Emanuel, ET Denisov, ZK Maizus (1965) Chain Oxidation Reactions of Hydrocarbons in the Liquid Phase, Nauka, Moscow.
- VA Poluektov, EI Babkina, IR Begishev (1974) On the Dependence of the Rate of a Chain Reaction on the Reactant Ratio, Dokady Akademii Nauk SSSR 215(3): 649-652.
- MM Silaev, LT Bugaenko (1992) Mathematical Simulation of the Kinetics of Radiation Induced Hydroxyalkylation of Ali- phatic Saturated Alcohols, Radiation Physics and Chemistry 40(1): 1-10.
- MM Silaev, LT Bugaenko (1994) Kinetics of the Addition of α-Hydroxyalkyl Radicals to 2-Propen-1-ol and Formaldehyde, Kinetics and Catalysis 35(4): 509-513.
- MM Silaev (1999) Competition Kinetics of Nonbranched Chain Processes of Free-Radical Addition to Double Bonds of Molecules with the Formation of 1:1 Adducts, Kinetics and Catalysis 40(2): 256-259.
- MM Silaev (2007) Simulation of the Nonbranched-Chain Addition of Saturated Free Radicals to Alkenes and Their Derivatives Yielding 1:1 Adducts, Theoretical Foundations of Chemical Engineering 41(3): 273- 278.
- MM Silaev (2007) Simulation of Nonbranched Chain Processes for Producing 1, 2-Alkanediols in Alcohol-Formaldehyde Systems, Theoretical Foundations Chemical Engineering 41(4): 357-361.
- MM Silaev (2001) A New Competitive Kinetic Model of Radical Chain Oxidation: Oxygen as an Auto inhibitor, Bio-physics 46(2): 202-207.
- MM Silaev (2007) Simulation of the Initiated Addition of Hydro-carbon Free Radicals and Hydrogen Atoms to Oxygen via a Nonbranched Chain Mechanism, Theoretical Foundation of Chemical Engineering 41(6): 831-838.
- Y Bard (1974) Nonlinear Parameter Estimation, Academic, New York, USA.
- L Bateman (1954) Alkene Oxidation, Quarterly Reviews 8(2): 147-167.
- WH Urry, FW Stacey, ES Huyser, OO Juveland (1954) The Peroxide and Light-Induced Additions of Alcohols to Alkenes, Journal of the American Chemical Society 76(2): 450-455.
- Urry WH, Juveland OO (1958) Free Radical Additions of Amines to Alkenes, Journal of the American Chemical Society 80(13): 3322-3328.
- AG Shostenko, PA Zagorets, AM Dodonov, AA Greish (1970) γ-Radiation- Induced Addition of Phosphorus Trichloride to Isobutylene, Khimiya Vysokikh Energii 4(4): 357.
- V Kim, AG Shostenko, MD Gasparyan (1979) Reactivity of Polychloroalkyl Radicals in the Telomerization of CCl4 with 1-Propene and 2-Methyl-1- Propene, Reaction Kinetics and Catalysis Letters 12(4): 479-484.
- VE Myshkin, AG Shostenko, PA Zagorets, KG Markova, AI Pchelkin (1977) Determination of Absolute Rate Constants for the Addition of the Ethyl Radical to Alkenes, Teoretich- eskaya i Eksperimental’naya Khimiya 13(2): 266-271.
- RA Zamyslov, AG Shostenko, IV Dobrov, NP Tarasova (1987) Kinetics of γ-Radiation-Induced Reactions of 2-Propanol with Trifluoropropene and Hexafluoropropene, Kinetika i Katalyz 28(4): 977-979.
- MM Silaev (1990) Dependence of Radiation-chemical γ-Diol Yields on the 2-Propen-1-ol Concentration in the Radiolysis of Aliphatic Saturated C1-C3 Alcohol + 2-Propen-1-ol Systems, Khimiya Vysokikh Energii 24(3): 282-283.
- MM Silaev (1994) γ-Diol Formation via the Auto oxidation of 2-Propen- 1-ol Solutions in Saturated Alcohols, Vestnik Mos- kovskogo Universiteta, Ser. 2: Khimiya 35(1): 40-42.
- LT Bugaenko, MG Kuzmin, LS Polak (1993) High-Energy Chemistry, Horwood Hall, New York, USA, p. 112.
- JK Thomas (1967) Pulse Radiolysis of Aqueous Solutions of Methyl Iodide and Methyl Bromide. The Reactions of Iodine Atoms and Methyl Radicals in Water, The Journal of the Physical Chemistry 71(6): 1919- 1925.
- JF Walker (1957) Formaldehyde, Reinhold, New York, 1953, English Translation under the title Formal’degid, Goskhimizdat, Moscow, p. 106.
- MM Silaev, AV Rudnev, EP Kalyazin (1979) Formaldehyde. III. Concentration of Free Formaldehyde as a Function of Temperature, Polarity of Solvents, and Total Concentration of Formaldehyde in Solution, Zhurnal Fizicheskoi Khimii 53(7): 1647-1651.
- Oyama M (1965) A Free-Radical Reaction of Primary and Secondary Alcohols with Formaldehyde, The Journal of Organic Chemistry 30(7): 2429-2432.
- GI Nikishin, D Lefor, ED Vorob’ev (1966) Free Radical Reaction of Primary Alcohols with Formaldehyde, Izvestiya Akademii Nauk SSSR, Ser. Khimiy 15(7): 1226-1227.
- MB Dzhurinskaya, AV Rudnev, EP Kalyazin (1984) High Temperature UV Photolysis of Formaldehyde in Liquid Methanol, Vestnik Moskovskogo Universiteta, Ser. 2: Khimiya 25(2): 173-176.
- EP Kalyazin, EP Petryaev, OI Shadyro (1977) Reaction between Oxyalkyl Radicals and Aldehydes, Zhurnal Or- ganicheskoi Khimii 13(2): 293-295
- AI Novoselov, AI Silaev, MM, LT Bugaenko (2004) Effect of Temperature on the Yields of Final Products in the γ-Radiolysis of Formaldehyde Solutions in C1-C3 Alkanol, High Energy Chemistry 38(4): 236-238.
- AI Novoselov, MM Silaev, LT Bugaenko (2008) Dependence of Ethanediol Yield on Formaldehyde Concentration in γ-Radiolysis of Methanol- Formaldehyde System at 373-473 K, High Energy Chemistry 42(1): 69- 70.
- AI Novoselov, MM Silaev, LT Bugaenko (2010) γ-Induced Single-Step Synthesis of Ethylene Glycol from Methanol-Formaldehyde Solution, Theoretical Foundation of Chemical Engineering 44(4): 432-435.
- AI Novoselov, MM Silaev, LT Bugaenko (2007) Dependence of 1,2-Propanediol Yield on Formaldehyde Concentration in γ-Radiolysis of Ethanol-Formaldehyde System at 373-473 K, High Energy Chemistry Vol 41(1): 53-54.
- SYa Pshezhetskii, AG Kotov, VK Milinchuk, VA Roginskii, VI Tupikov, et al. (1972) ESR of Free Radicals in Radiation Chemistry, Khimiya, Moscow.
- MM Silaev (1993) Estimating the Solvent Concentration in Formaldehyde Solutions at Various Temperatures, Zhurnal Fizi- cheskoy Khimii 67(9): 1944.
- MM Silaev (2002) Applied Aspects of the γ-Radiolysis of C1-C4 Alcohols and Binary Mixtures on Their Basis, High Energy Chemistry 36(2): 70- 75.
- MM Silaev, LT Bugaenko, EP Kalyazin (1986) On the Possibility of Adequately Estimating the Rate Constants for the Reaction of Hydroxyalkyl Radicals with Each Other Using the Self-Diffusion Coefficients or Viscosities of the Corresponding Alcohols, Vestnik Moskovskogo. Univiversiteta, Ser. 2: Khimiya 27(4): 386-389.
- OI Shadyro (1975) Radiation-chemical Conversions of Aldehydes in Various Systems, Ph.D. Thesis (Chemistry), Belarusian State University, Minsk.
- MM Silaev (1993) Relative Reactivity of α-Hydroxyethyl Radicals for 2-Propene-1-ol and Formaldehyde Double-Bond Addition, Vestnik Moskovskogo Universiteta, Ser. 2: Khimiya, 34(3): 311.
- H Seki, R Nagai, M Imamura (1968) γ-Radiolysis of a Binary Mixture of Methanol and Water. The Formation of Formaldehyde in the Radiolysis of Liquid Methanol, Bulletin of the Chemical Society of Japan 41(12): 2877-2881.
- VYa Shtern (1964) Mechanism of the Gas-Phase Oxidation of Hydrocarbons, Akademiya Nauk SSSR, Moscow.
- HLJ Bäckström (1934) Der Kettenmechanismus bei der Autoxydation von Aldehyden, Zeitschrift für physikalische Chemie (B), Bd. 25(1-2): Sn. 99-121.
- AA Aliev, VV Saraeva (1983) Isomerization of Peroxy Radicals Resulting from the Radiation-Induced Oxidation of oXylene, Vestnik Moskovskogo Universiteta, Ser. 2: Khimiya 34(4): 371-374.
- EJ Badin (1948) The Reaction between Atomic Hydrogen and Molecular Oxygen at Low Pressures. Surface Effects, Journal of the American Chemistry Society 70(11): 3651-3655.
- AL Buchachenko (1984) Complexes of Radicals and Dioxygen with Organic Molecules, IP Beletskaya, Editor, Nauka, Moscow.
- JS Francisco, IH Williams (1988) The Thermochemistry of Polyoxides and Polyoxy Radicals, International Journal of Chemical Kinetics 20(6): 455-466.
- VN Kokorev, NN Vyshinskii, VP Maslennikov, IA Abronin, GM Zhidomirov, et al. (1981) Electronic Structure and Chemical Reactions of Peroxides: I. MINDO/3 Calculation of the Geometry and Enthalpy of Formation of the Ground States of Organic and Organoelement Peroxides, Zhurnal Strukturnoi Khimii 22(4): 485-491.
- F Dmitruk, VV Lobanov, LI Kholoimova (1986) Role of Tetroxide Conformation in the Mechanism of Peroxy Radical Recombination Teoreticheskaya i Experimental naya Khimiya 22(3): 363-366.
- VA Belyakov, RF Vasilev, NM Ivanova, BF Minaev, OV Osyaeva, et al. (1987) Electronic Model of the Excitation of Chemiluminescence in the Oxidation of Organic Compounds, Izvestiya Akademii Nauk SSSR, Ser.: Fizika, 51(3): 540-547.
- P Ase, W Bock, A Snelson (1986) Alkylperoxy and Alkyl Radicals. 1. Infrared Spectra of CH3 O2 and CH3O4 CH3 and the Ultraviolet Photolysis of CH3 O2 in Argon + Oxygen Matrices. The Journal of Physical Chemistry 90(10): 2099-2109.
- GC Pimentel, AL McClellan (1960) The Hydrogen Bond, L Pauling, Editor, Freeman, San Francisco, pp. 200.
- GA Russell (1957) Deuterium Isotope Effects in the Auto oxidation of Aralkyl Hydrocarbons: Mechanism of the Interaction of Peroxy Radicals. Journal of the American Chemical Society 79(14): 3871-3877.
- MM Silaev (1999) The Competition Kinetics of No branched Chain Processes of Free Radical Addition to Double Bonds of Molecules with the Formation of 1:1 Adducts and the Inhibition by the Substrate”, Oxidation Communication 22(2): 159-170.
- MM Silaev (1999) The Competition Kinetics of Radical Chain Addition Zhurnal Fizicheskoi Khimii. 73(7): 1180-1184 English Translation in: Russian. Journal of Physical Chemistry 73(7): 1050-1054.
- AP Darmanyan, DD Gregory, Y Guo, WS Jenks, L Burel, et al. (1998) Quenching of Singlet Oxygen by Oxygen and Sulfur Centered Radicals: Evidence for Energy Transfer to Peroxy Radicals in Solution Journal of the American Chemistry Society 120(2): 396-403.
- JR Kanofsky (1986) Singlet Oxygen Production from the Reactions of Alkylperoxy Radicals. Evidence from 1268nm Chemilu minescence. The Journal of Organic Chemistry 51(17): 3386-3388.
- NN Semenov (1934) Tsepnye reaktsii (Chain Reactions), Goskhimtekhizdat, Leningrad, pp. 241, 203.
- M Reznikovskii, Z Tarasova, B Dogadkin (1950) Oxygen Solubility in Some Organic Liquids Zhurnal Obshchei Khimii 20(1): 63-67.
- JA Howard, KU Ingold (1967) Absolute Rate Constants for Hydrocarbon Auto oxidation. VI. Alkyl Aromatic and Alkeneic Hydrocarbons. Canadian Journal of Chemistry 45(8): 793-802
- NF Barr, AO Allen (1959) Hydrogen Atoms in the Radiolysis of Water. The Journal of Physical Chemistry 63(6): 928-931.
- HA Smith, A Napravnik (1940) Photochemical Oxidation of Hydrogen. Journal of the American Chemistry Society 62(1): 385-393.
- PB Pagsberg, J Eriksen, HC Christensen (1979) Pulse Radiolysis of Gaseous Ammonia Oxygen Mixtures. The Journal of Physical Chemistry 83(5): 582-590.
- MM Silaev (2003) Competitive Mechanism of the Non branched Radical Chain Oxidation of Hydrogen Involving the Free Cyclohydrotetraoxyl Radical [ОО···Н···ОО]• which Inhibits the Chain Process, Khimiya Vysokikh Energii 37(1): 27-32. English Translation in: High Energy Chemistry, 37(1): 24-28.
- MM Silaev (2008) Simulation of Initiated Non branched Chain Oxidation of Hydrogen: Oxygen as an Auto inhibitor, Khimiya Vysokikh Energii 42(2): 124-129. English Translation in: High Energy Chemistry 42(1): 95-100.
- DJ McKay, JS Wright (1998) How Long Can You Make an Oxygen Chain? Journal of the American Chemistry Society 120(5): 1003-1013.
- NP Lipikhin Dimers (1975) Clusters, and Cluster Ions of Oxygen in the Gas Phase. Uspekhi Khimii 44(8): pp. 366-376.
- SD Razumovskii (1979) Kislorod elementarnye formy i svoistva (“Oxygen: Elementary Forms and Properties”), Khimiya, Moscow.
- KM Dunn, GE Scuceria, HF Schaefer (1990) The infrared spectrum of cyclotetraoxygen O4: a theoretical investigation employing the single and double excitation coupled cluster method. The Journal of Chemical Physics 92(10): 6077-6080.
- L Brown, V Vaida (1996) Photo reactivity of Oxygen Dimers in the Ultraviolet. The Journal of Physical Chemistry 100(19): 7849-7853.
- V Aquilanti, D Ascenzi, M Bartolomei, D Cappelletti, S Cavalli, et al. (1999) Molecular Beam Scattering of Aligned Oxygen Molecules. The Nature of the Bond in the O2- O2 Dimer. Journal of the American Chemistry Society 121(46): 10794-1080.
- F Cacace, G de Petris, A Troiani (2001) Experimental Detection of Tetra oxygen. Angewandte Chemie, Internation Edition (in English) 40(21): 4062-4065.
- HS Taylor (1926) Photosensitization and the Mechanism of Chemical Reactions. Transactions of the Faraday Society 21(63(3)): 560-568.
- AB Nalbandyan, VV Voevodskii (1949) Mekhanizm okisleniya i goreniya vodoroda (“Mechanism of Hydrogen Oxidation and Combustion”), VN Kondratev, Editor, Akad. Nauk SSSR, Moscow.
- SN Foner, RL Hudson (1962) Mass spectrometry of the H O2 free radical. The Journal of Chemical Physics 36(10): 2681.
- CJ Hochanadel, JA Ghormley, PJ Ogren (1972) Absorption Spectrum and Reaction Kinetics of the H O2 Radical in the Gas Phase. The Journal of Chemical Physics 56(9): 4426-4432.
- JB Robertson (1954) A Mass Spectral Search for H2O4 and HO4 in a Gaseous Mixture Containing H O2 and O2. Chemistry and Industry 48: 1485.
- D Bahnemann, EJ Hart (1982) Rate Constants of the Reaction of the Hydrated Electron and Hydroxyl Radical with Ozone in Aqueous Solution. The Journal of Physical Chemistry 86(2): 252-255.
- ND Sokolov (1981) Vodorodnaya svyaz: Sbornik statei (“The Hydrogen Bonding: Collection of Articles”) Editor, Nauka, Moscow.
- J Staehelin, RE Bühler, J Hoigné (1984) Ozone Decomposition in Water Studied by Pulse Radiolysis. 2. OH and HO4 as Chain Intermediates. The Journal of Physical Chemistry 88(24): 5999-6004.
- F Cacace, G de Petris, F Pepi, A Troiani (1999) Experimental Detection of Hydrogen Trioxide. Science 285(5424): 81-82.
- RF Bühler, J Staehelin, J Hoigné (1984) Ozone Decomposition in Water Studied by Pulse Radiolysis. 1. H O2/O - and HO3/O - as Intermediates. The Journal of Physical Chemistry 88(12): 2560-2564.
- IV Trushkov, MM Silaev, ND Chuvylkin Acyclic and Cyclic Forms of the Radicals 4 HO• , 3 4 CH O• , 2 5 4 C H O•Ab Initio Quantum Chemical Calculations”, IzvestiyaAkademii Nauk, Ser.: Khimiya, No. 3, 2009, 479-482, English Translation in: Russian Chemical Bulletin, International Edition, Vol. 58, No. 3, 2009, 489-492.and 1176-1182.
- A Mansergas, JM Anglada, S Olivella, MF Ruiz López (2007) On the Nature of the Unusually Long OO Bond in HO3 and HO4 Radicals. Phys. Chem. Chem. Phys. 9(44): 5865-5873.
- W Wong, DD Davis (1974) A Flash Photolysis Resonance Fluorescence Study of the Reactions of Atomic Hydrogen and Molecular Oxygen: H + O2 + M → H O2 + M. International Journal of Chemical Kinetics, 6(3): pp. 401-416.
- X Xu, RP Muller, WA Goddard (2002) The Gas Phase Reaction of Singlet Dioxygen with Water: a Water Catalyzed Mechanism. Proceedings of the National Academy Sciences of the United States of America 99(6): 3376- 3381.
- ET Seidl, HF Schaefer (2000) Is There a Transition State for the Unimolecular Dissociation of Cyclotetraoxygen (O4)? The Journal of Chemical Physics 96(2): pp.Chemistry 40(1): 29-35.
- R Hernández Lamoneda, A Ramírez Solís (2000) Reactivity and Electronic States of O4 along Minimum Energy Paths. The Journal of Chemical Physics 113(10): 4139-4145.
- AJC Varandas, L Zhang (2000) Test Studies on the Potential Energy Surface and Rate Constant for the OH + O3 Atmospheric Reaction. Chemical Physics Letters 331(5-6): 474-482.
- (1991) Atmosfera Spravochnik (“Atmosphere: A Handbook”), Gidrometeoizdat, Leningrad.
- H Okabe (1978) Photochemistry of Small Molecules. Wiley, New York, USA.
- AK Pikaev (1986) Sovremennaya radiatsionnaya khimiya. Radioliz gazov i zhidkostei (“Modern Radiation Chemistry: Radiolysis of Gases and Liquids, Nauka, Moscow.
- AW Boyd, C Willis, OA Miller (1971) A Re examination of the Yields in the High Dose Rate Radiolysis of Gaseous Ammonia. Canadian Journal of Chemistry 49(13): 2283-2289.
- MM Silaev (2000) Competition Mechanism of Substrate Inhibited Radical Chain Addition to Double Bond Neftekhimiya, Vol.C H O•: Ab Initio Quantum Chemical Calculations, Izvestiya 40(1): pp. 33-40, English Translation in: Peroleum 2 5 4.
- MM Silaev (2003) Competition Kinetics of Non branched Chain Processes of Free Radical Addition to the C=C, C=O, and O=O Double Bonds of Molecules. Neftekhimiya 43(4): pp. 302-307, English Translation in: Petroleum Chemistry 43(4): 258-273.
- MM Silaev (2005) Low reactive Free Radicals Inhibiting Non-branched Chain Processes of Addition. Biofizika 50(4): pp. 585-600, English Translation in: Biophysics, 50(4): 511-524.
- RT Sanderson (1982) Radical Reorganization and Bond Energies in Organic Molecules. The Journal of Organic Chemistry 47(20): 3835- 3839.
- IV Vereshchinskii, AK Pikaev (1963) “Vvedenie v radi atsionnuyu khimiyu” (“Introduction to Radiation Chemistry”), Spitsyn, VI. Editor, Akademiya Nauk SSSR, Moscow, pp. 190.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...