Lupine Publishers Group
Lupine Publishers
Menu
Review Article (ISSN: 2770-5447)
Physics of the Ventricular Vortex in Dilated Cardiomyopathy Volume 3 - Issue 3
Trainini Jorge MD, PhD*1,Lowenstein Jorge MD2, Beraudo Mario MD3, Wernicke Mario MD4, Jesús Valle, PhD5, Lowenstein-Haber Diego MD2, Labrada Luis MD6, Trainini Alejandro MD1,3 and Bastarrica María Elena MD3
- 1Department of Cardiac Surgery, Hospital Presidente Perón, Buenos Aires, Argentina.
- 2Department of Cardiology, Investigaciones Médicas, Buenos Aires, Argentina.
- 3Department of Cardiac Surgery, Clínica Güemes , Luján , Buenos Aires, Argentina.
- 4Department of Pathology, Clínica Güemes , Luján , Buenos Aires, Argentina.
- 5National Institute for Aerospace Technology - General Subdirectorate for Naval Systems, Madrid, España.
- 6Deparment of Cardiology, Clínica Havanamed. Medellín, Colombia
Received:April 08, 2021; Published: April 20, 2021
Corresponding author: Trainini Jorge MD, PhD, Department of Cardiac Surgery, Hospital Presidente Perón, Buenos Aires, Argentina
DOI: 10.32474/ACR.2021.03.000165
Abstract
The role of the vortex in cardiac remodeling should be understood as an etiopathogenic factor in the myocardial wall with its consequent dilation and not as a cause of this wall’s alteration. It is not necessary to consider the random molecular behavior in the intraventricular vortex as maximum unpredictability. Randomness becomes uniformity. For example, in a balloon, particles move in all directions but exert the same pressure. This is analogous to the left ventricle: molecules collide against each other as a dense and anarchic crowd. A fluid applies pressure on the surface with which it makes contact, but if the chaotic elements become ordered, we have regularity. A milliliter of blood contains around one hundred trillion particles. It is impossible to combine their equations. Probability in statistics was used to find regularity in global and average behavior. The random state of molecular chaos (turbulence) that occurs in the intraventricular vortex alters the wall. Remodeling leading to volume overload starts when 20% of the ventricular mass is compromised. With increased volume there is more sphericity and vice versa. Thus, fluid becomes a sculptor of the ventricular wall through the velocity of fluid particles colliding against its walls.
Keywords: Intraventricular vortex; Dilated cardiomyopathy; Myocardial torsion
Ventricular Vortex
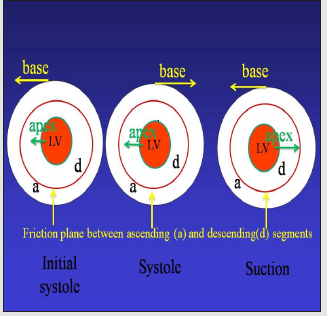
The blood vortex generated in the left ventricle resulting in systolic ejection can be explained through the theory of “dissipative structures”, developed by Ilya Prigogine[1]. The helical anatomy of the heart and the ensuing torsion arising from this structure determine the intraventricular vortex (Figures 1 to 3).[2,3] The ejected blood flow is derived from a source of instability. It occurs through the coexistence of structure (ventricular chamber) and function (ejection). This trinomial of structure, function and flow implies a feedback system in which flow is subjected to continuous fluctuations leading to the reorganization of the system. What happens with the origin and progression of the intraventricular vortex? The helical arrangement of the myocardium leads in its function to an opposite rotation between the apex and the base of the heart, a situation that allows ventricular twisting (systolic contraction) and untwisting (ventricular suction) (Figure 3).[4,5] The anatomical basis is determined by the arrangement of the descending and ascending segments, which rotate in opposite directions allowing ventricular twisting-untwisting. This divergent direction in the apical and base rotation produces ventricular blood content instability and the development of a vortex, a consequence arising from the need of the myocardial mass to generate the necessary force to pump blood throughout the whole system. Ventricular torsion is a functional requirement that correlates with the image in 8 adopted by the myocardium.
Figure 1: Myocardial band. RV: right ventricle; PIS: posterior interventricular sulcus; AIS: anterior interventricular sulcus; LV: left ventricle.
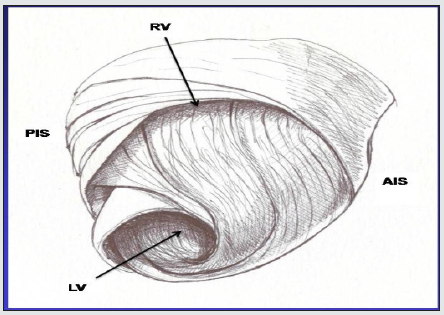
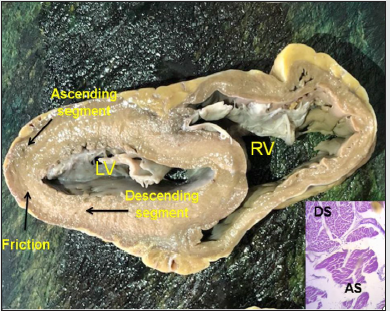
Figure 2: Transverse section of the left and right ventricles (human heart). The black arrows indicate the direction of motion of each segment during systole and the plane of friction between both segments. The histology shows the different orientation of the longitudinal fibers of the ascending segment (AS) in relation to the transverse fibers of the descending segment (DS).
The “dissipative structures” theory is based on the concept
of the physicist Henri Bénard (1874-1939), which describes the
instability of a stationary system leading to its auto-organization.
In this experiment, a thin fluid layer is submitted to a thermal
difference between the heated inferior layer and the superior layer
in contact with the environment. The instability is produced by a
vertical temperature gradient in the horizontal fluid layer. The
inferior layer attains a higher temperature than the superior one,
producing an upward heat flow. For small gradients, heat diffuses
by conduction, but if it reaches a critical value, there is convection.
Upon achieving an adequate temperature threshold, the resting
state of the fluid becomes unstable: there is convection, that is,
the coherent movement of an enormous amount of molecules.
The threshold is thus the critical value from which the system
becomes unstable, producing fluctuations. If these go beyond the
stability threshold, the system is transformed leading to its autoorganization,
with the emergence of a qualitatively different mode
of function.
Hydrodynamics, due to turbulence, constitutes a good example
of Bénard’s instability. When convection appears in inestability it
leads to the spatial auto-organization of the system. If the system is
observed vertically (at its output), a regular hexagonal arrangement
is seen, similar to the cells of a beehive. These fluctuations lead to
an order, produced by non-equilibrium.
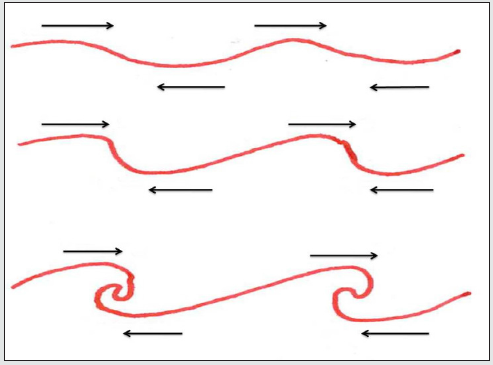
Figure 4: Evolution of instability. Turbulence. The process developing turbulence is produced as a consequence of the radical change in speed at both sides of the separation.
Blood flows from the left ventricle towards the aorta forming
a vortex that presents two established shapes: spiral and funnel.
Ventricular torsion produces this turbulence because of the
different speed at both sides of its surface (Figure 4). The anatomical
arrangement (structure) described by the myocardial band theory
and the resulting function contributes to its development. This is
echocardiographically supported by the presence of greater radial
strain at the basal and medial levels of the left ventricle due to the
prevalence of transverse fibers, while oblique fibers towards the
apex are responsible of greater longitudinal and circumferential
strain with a clear predominance of apical rotation. This opposing
motion from the base to the apex gives origin to systolic torsion
[6-8].
As a result, blood increases its speed as it gets near the aortic
output orifice. At first, flow tends to be uniform, but does not
preserve this condition due to the irregularities present in the
ventricular chamber and in blood motion. This situation triggers
an afference difference in the rotational spiral motion of blood
flow, increasing radial as well as rotational speed as the vortex
diameter decreases. Blood moves with a helical motion, describing
a pipe of narrowing flow lines, called vortex. The pipe of this
vortex is constrained by the blood that applies pressure on all its
circumference This decreases its radius and increases rotation,
thus developing instability in the initial uniform flow.
Ventricular muscle pressure and blood pressure and the
progressively reduced radius combine to accelerate the helical
motion of blood with the concomitant increase in velocity.
Eventually, a miniature eddy is formed (Figure 5), generating linear
and non-linear structures. The forces acting to shape the vortex feed
back unto themselves allowing it to act as a unit. In this instability,
there is rupture in the spatial symmetry of the vortex leading
from chaos to coherence. The trapped molecules in this vortex are
no longer independent of one another. Figures 6 and 7 show the
change of the non-linear chaos, forming the blood vortex, to a linear
orderliness of blood flow at the aortic output [9]. This linear aortic
flow implies a reorganization throughout the non-linearity of the
intraventricular vortex. The system’s turbulence leads it into a new
state. It is an organizer. The price is a permanent creation of chaos.
Figure 5: Echocardiographic vortex imges of the left ventricule and outflow tract with heigh frame rate without contrast.
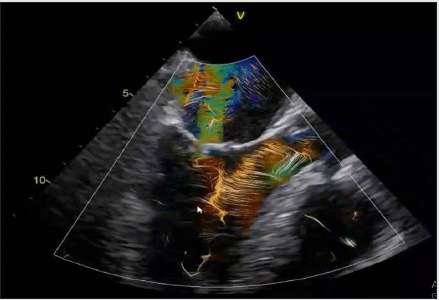
Figure 6: Left ventricule vortex with contrast agent showing the change from non-linear chaos forming the blood eddy ( small arrows) to the orderliness of blood flow towards the aorta ( larger arrows) modified from Hong et al. J Am Coll Cardiol Img.2008;1: 705-717.
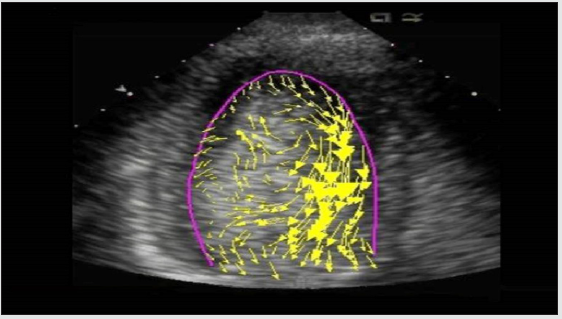
Figure 7: Left ventricular modeling . The figures shows the new order of ventricular outflow in systole compared with end diastole.
In Bénard’s vortices there is a temporal symmetry rupture.
The molecules abandon the incoherent motion they had to
adopt coherence. There are new states far from equilibrium.
Independently of gaseous, liquid or crystalline equilibrium states,
they all respond to an essential trait that differentiates them from
the non-equilibrium states described in vortices or turbulences.
Vorticity appears when there is a relative rotation of some
particles of the fluid with respect to others. The dynamics established
by ventricular torsion, due to the crossover of the descending and
ascending segment, causes the intraventricular fluid to adopt the
characteristics of a vortex with turbulent flow that tends to linearity
when it is ejected. Laminar flow is irrotational, this means that
there cannot be vorticity. Why is there an intraventricular turbulent
flow which we call vortex? Turbulence modifies parameters such as
resistance to friction, heat transmission and mixing ability. Maybe
the answer is to homogenize the blood to be distributed throughout
the body, but it should also be acknowledged that this turbulence is
the result of the ventricular torsion necessary to eject the fluid at
high velocity.
In the ventricle, there can be no laminar flow, as the flow
velocity is high and the chamber diameter is not small, a situation
that invalidates parallel currents, called laminar movements. As
the fluid is disturbed by ventricular torsion, a turbulent motion is
established. The characteristic of this flow is its irregular, dissipative
nature. If no energy is delivered, turbulence declines and this is
what happens with the energetic slope during the ejective period,
between the more active and less active phases of the cardiac cycle.
These turbulent motions are always rotational and threedimensional.
There are no two-dimensional flows. Turbulence is
not a property of fluid but of flow and is produced by ventricular
torsion. Small perturbations make flow unstable. Infinitesimal
perturbations grow spontaneously. The process of vortex
development is produced due to the radical change in speed as a
result of ventricular torsion. This torsion not only has the effect of
generating enough energy but also of avoiding the blood content
from affixing in peripheral ventricular locations by thoroughly
washing its walls with the vortex.
Turbulence is determined by a maze of eddies which are
drawn by gradients of velocity and by the interaction with other
eddies. This process of division continues until the scale of eddies
is so small that, with logically low Reynolds numbers, they prevent
the persistence of instability. To determine the regime in which a
fluid is, in internal flows, the Reynolds number is used, (Re) which
is a dimensionless number (without physical dimensions) that
takes into account the speed of the fluid, the local diameter of the
geometry, dynamic viscosity and fluid density: whenever Re <2300
the flow will be laminar, if Re> 4000 the flow will be turbulent, and
between 2300 and 4000 the flow is transitional.
Molecular Chaos
Blood is a Brownian, non-Newtonian fluid; therefore, it is not
homogeneous and subject to molecular chaos. Leucippus, in 440
BCE, introduced a word whose meaning implied “that it cannot be
cut”. He thus inaugurated the concept of atom. Democritus (V-IV
BCE) progressed in its study, leading to the existence of vacuum,
denied by Anaxagoras (500-428 BCE) and defended by Epicurus
(341-270 BCE). It was necessary to wait untilLucretius (95-55
BCE) to renew its interest, but the microscopic movement was
only developed by Daniel Bernoulli (1700-1782) in 1738 when he
sustained that gases were composed of small particles (a theory
extended to fluids). In view of the possibility that the whole
universe was composed of moving and colliding atoms, Pierre-
Simon Laplace (1749-1827), established a determinist concept:
“[For a superior intelligence]… the future, as well as the past, would
be present before its eyes”.
The challenge was to extend this idea to mechanics, which
was inaugurated by Nicholas Léonard Sadi Carnot (1796-1832),
when he tried to optimize the efficiency of steam engines. In 1824
he established the efficiency of fuel in steam engines, laying the
foundation of thermodynamics. Heat had to flow from a hot to a
cold body. Benjamin Thompson (1753-1814) gave an essential
step in heat compression by stating that this was produced by the
random movement of atoms (Figure 8).
Figure 8: Motion and collisions of a particle determine a random path. Rudolph Clausius formulated the term “average free path” before collision of a particle with another one.

Rudolph Clausius (1822-1888) is a fundamental figure. He
confirmed that heat goes from a hot to a cold body and progresses in
a direction where, if processes are irreversible, time is an arrow. He
developed the concept of the second law of thermodynamics called
entropy, which comes from the Greek word “trope” and means
evolution or transformation. Entropy measures the amount of
molecular disorder in a system. Clausius also established the basis
of the kinetic theory of gases. In 1854, Hermann von Helmholtz
(1821-1894) explained the end of this dissipation of heat in the
universe until reaching thermal death.
James Clerk Maxwell (1831-1879) introduced probability.
He postulated that a distribution function is the practical
characterization of a huge set of molecules. It was more logical to
ask oneself how many particles are in a certain range of velocities
than looking at each particle individually. He established that what
is important is not the trajectory of each particle but their mean
behavior. Fluids should be considered a collection of molecules with
random behavior, colliding between them and against the walls
of the receptacle (Figure 8). Pressure is no more than the effect
of collisions between molecules and the walls of the container.
Temperature is a measure of the energy of particles and the average
kinetic energy behaves the same as temperature. The greater the
turbulence, the greater the velocity of collision with temperature
increase. The state of the system is given by the number of molecules
and their energy charges.
The concept of Brownian motion belongs to Robert Brown
(1773-1858), who observed the frenzied dance of pollen grains
in water. Albert Einstein (1879-1955) explained this diffusion
which was later corroborated by him and Jean Perrin (1870-1942).
Thermodynamics was developed since the Industrial Revolution.
Almost at the same time, Ludwig Boltzmann (1844-1906) was
born, who applied probability to physics. He thus considered that
thermodynamics was reduced to the complementarity between
mechanics and probability. He supported this concept with the
atomic theory, assuming that due to the reduced size and great
number of atoms, the way of understanding a set of particles was
through statistics. Boltzmann devoted all his life to explain the
second law of thermodynamics in mechanical terms. He associated
entropy with probability. The greater the probability, the higher the
entropy. In 1866 he published “The mechanical significance of the
second law of thermodynamics” and in 1872 “New studies on the
thermal equilibrium of gas molecules”. He based his study in the
law of the atomic theory and used Daniel Bernoulli’s kinetic theory
of gases, who had declared that fluids were aggregates of particles
in constant motion.
Consequence of Vortex in Dilated Cardiomyopathy
Diagnosis and treatment of heart failure is limited by the
difficult acquisition of noninvasive quantitative indices of cardiac
physiology. The study of velocity vectors, movable geometry,
pressure-volume loops, left ventricular elastic wall stress-strain
relationships, the importance of the vortex and its role as mechanical
energy storage, together with the dependence of its properties, can
provide accurate information for therapeutic decision-making,
follow-up and prognosis [10].
Intraventricular blood fluid (molecular chaos) models the
preservation of dilated cardiomyopathy though the vortex, which
is the result of myocardial torsion. It must be understood that for
the elastic walls of a container such as the myocardium, blood
fluid in the ventricular chamber behaves in the vortex mechanism
as a chaotic molecular state, perpetuating remodeling [11]. This
process is due to the continuous collision of particles and their
constant change of direction. The simulation of biological processes
is an unexplored field with a limited number of devices that have
started to develop computational simulation models almost always
directed to a virtual visualization concept and lacking an adequate
scientific model of fluid behavior.
It is not known how to model blood from a dynamic-fluid
perspective. Blood is a much more complex fluid than any other
homogeneous liquid. It is defined as a non-Newtonian fluid, whose
viscosity changes with the gradient of tension applied to it, and
whose frictional shear stresses are directly proportional to the
velocity gradient. As a result, different from a Newtonian fluid, a non-
Newtonian fluid does not have a constant defined viscosity. It is also
necessary to couple fluid simulation to an elastic deformable system
such as arteries and the heart. Studies carried out so far provided
stiff geometries, so it is necessary to integrate fluid mechanics
with elastic or deformable structures. Imaging techniques supply
sufficient information for therapeutic decision-making. However,
there are groups of patients with inadequate indication provided
by these techniques to make therapeutic decisions based on
scientific evidence. As examples we can mention patients with
small diameter aneurysms but at risk of rupture or those with
heart failure and preserved ejection fraction. The diagnosis can
be enhanced with the development of simulation systems able
to study intraventricular flow velocities and characteristics,
pressure differences and quantitative myocardial contractility and
distensibility indices. The characterization of these indices will
deliver the necessary information for precise therapeutic decisionmaking,
predict the behavior of a specific repair and assess the riskbenefits
of a surgical intervention.
In fact, the role of the vortex in cardiac remodeling should be
understood as an etiopathogenic factor in the myocardial wall with
its consequent dilation and not as a cause of this wall’s alteration. It
is not necessary to consider the random molecular behavior in the
intraventricular vortex as maximum unpredictability. Randomness
becomes uniformity. For example, in a balloon, particles move in
all directions but exert the same pressure. This is analogous to
the left ventricle: molecules collide against each other as a dense
and anarchic crowd. A fluid applies pressure on the surface
with which it makes contact, but if the chaotic elements become
ordered, we have regularity. A milliliter of blood contains around
one hundred trillion particles. It is impossible to combine their
equations. Probability in statistics was used to find regularity in global and average behavior. The random state of molecular chaos
(turbulence) that occurs in the intraventricular vortex alters the
wall. Remodeling leading to volume overload starts when 20% of
the ventricular mass is compromised. With increased volume there
is more sphericity and vice versa. Thus, fluid becomes a sculptor of
the ventricular wall through the velocity of fluid particles colliding
against its walls.
References
- Prigogine I (1967) “Introduction to thermodynamics of irreversible processes”. Intersciences, New York,
- Trainini JC, Lowenstein J, Beraudo M, Wernicke M, Trainini A, et al. (2020) Myocardial torsion and cardiac fulcrum (Torsion myocardique et pivot cardiaque). Morphologie 105(348): 15-23.
- Mora Llabata V, Roldán Torresa I, Saurí Ortiza A, Fernández Galera R (2016) Monteagudo Viana M, Romero Dorta E, Cosín Aguilar JA, Trainini J, Lowenstein J. Correspondence of myocardial strain with Torrent-Guasp’ s theory. Contributions of new echocardiographic parameters. Rev Arg Cardiol 84: 541-549.
- Mora V, Roldán I. Romero E, Saurí A, Romero D, et al. (2018) Myocardial contraction during the diastolic isovolumetric period: analysis of longitudinal strain by means of speckle tracking echocardiography. J Cardiovasc Dev Dis 5(3): 41.
- Trainini JC, Elencwajg B, López-Cabanillas N, Herreros J, Lowenstein J Bustamante-Munguira J, et al. (2017) Ventricular torsion and cardiac suction effect: The electrophysiological analysis of the cardiac band muscle. Interventional Cardiol 9 (1): 45-51.
- Wu MT, Tseng WYI, Su MYM, Liu ChP, Chiou KR, et al. (2006) Diffusion tensor magnetic resonance imaging mapping the fiber architecture remodeling in human myocardium after infarction. Correlation with viability and wall motion. Circulation 114(10): 1036-1045.
- Sengupta PP, Krishnamoorthy VK, Korinek J, Narula J, Vannan MA, et al. (2007) Left ventricular form and function revisited: applied translational science to cardiovascular ultrasound imaging. J Am Soc Echocardiogr 20(5): 539-551.
- Carreras F, Ballester M, Pujadas S, Leta R, Pons-Lladó G (2006) Morphological and functional evidences of the helical heart from non-invasive cardiac imaging. Eur J Cardiothoracic Surg 29(Suppl 1): S50-55.
- Valle J, Herreros J, Trainini J, García-Jimenez E, Talents M, et al. (2017) Three-dimensional definition of Torrent Guasp´s ventricular muscle band and its correlation with electric activation of the left ventricle (abstract). XXIII Congreso SEIQ, Madrid, España,. BJS, vol 105: s2.
- Álamo JC, Marsden AL, Lasheras JC (2009) Avances en mecánica computacional para el diagnóstico y tratamiento de la enfermedad cardiovascular. Rev Esp Cardiol 62: 781-805.
- Gómez Doblas JJ, De Teresa E, Lamas GA (1999) Geometría ventricular e insuficiencia cardiaca. Rev Esp Cardiol 52: 47-52.

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...