A novel improved PNGV model parameter identification of lithium battery based on double exponential fitting Volume 1 - Issue 2

Xiao Yanga, Shunli Wanga*, Wenhua Xua, Carlos Fernandezb, Chunmei Yua, Yongcun Fana, Wen Caoa

• School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China
• School of Pharmacy and Life Sciences, Robert Gordon University, Aberdeen AB10-7GJ, UK.

Received: September 08,2020   Published: September 30, 2020

Corresponding author: Shun-Li Wang, School of Information Engineering, Southwest University of Science and Technology, Mianyang 621010, China

DOI: 10.32474/JBRS.2020.01.000110

 

Abstract PDF

Abstract

In order to establish a more accurate battery equivalent model, the polarization circuit of the existing PNGV equivalent model is extended to characterize the polarization characteristics of the battery better. The double exponential fitting method is used in the parameter identification to improve the accuracy of parameter identification of battery equivalent model. With the results of hybrid pulse power characterization experiment, the parameters of improved model are identified. And obtain the functional relationship between parameters and state of charge through fitting. At last, a real-time simulation model is established. The simulation results show that the error value between the simulation model voltage and the actual voltage is less than 1.2%, the model accuracy is high. This lays the foundation for the estimation of the state of charge of the lithium battery in the follow-up work.

Keywords: Lithium Battery; Parameter Identification; improved PNGV model; double exponential fitting

Introduction

With the rise of new energy technology, power battery technology has developed rapidly, and lithium batteries are the main body of power batteries now [1]. In the process of energy storage and energy supply, the working status monitoring and energy management of the battery are completed by the battery management system. As a key factor in evaluating the quality of a battery management system, accurate estimation of State of Charge (SOC) is essential [2].
To estimate the SOC value of lithium batteries accurately, a reasonable battery equivalent model must be established [3]. The Rint model, PNGV model, Thevenin model and GNL model are widely used [4]. The above models perform well in simulating battery operating characteristics, but the model structure is complicated and the parameter solving is difficult [5].
In order to improve the accuracy of battery simulation and simplify the parameter calculation process, the existing PNGV model has been improved. The double exponential fitting method is used in the process of model parameter identification, finally the parameter identification results are verified by simulation. This laid the foundation for the SOC estimation of lithium batteries in follow-up research.

Mathematical analysis

a. Equivalent modeling

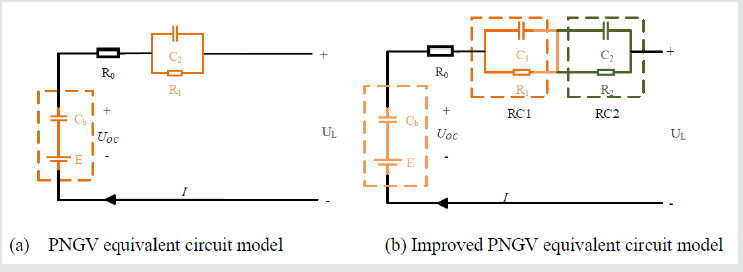
Traditional PNGV model has insufficient simulation accuracy in terms of battery capacity and the nonlinear relationship between UOC and SOC, so an improved PNGV equivalent model is established [6]. The improved model optimizes the polarization circuit, so that the dynamic characteristics of the battery can be better expressed. The PNGV model and its improved model are shown in Figure [1].
In Figure 1(b), the R1C1 and R2C2 respectively represents the process of rapid change and slow stability of the circuit voltage. Assuming that the current direction in the figure are positive, the voltages at both ends of the R1C1 and R2C2 network are represented by U1 and U2. For the circuit KVL equation, as shown in Eq. 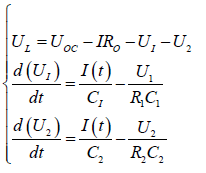(1).

(1)

b. Curve fitting and parameter identification

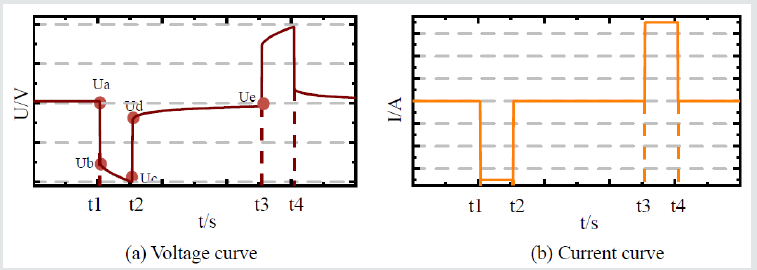
[Figure 2] shows the graph of the voltage and current changes during one cycle of charging and discharging in the Hybrid Pulse Power Pharacterization (HPPC) experiment. In the [figure] t1 is the discharge start time, t2 is the discharge stop time, and t3 is the static stop time.

It can be seen in the figure that, affected by the internal resistance of the battery R0, the terminal voltage of the battery will change dramatically at the time when the discharge start and stop [7]. So, the internal resistance of the equivalent circuit model can be deduced from Ohm’s law, and the internal resistance calculation formula is shown in Eq. 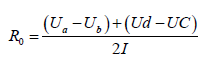(2).

(2)

The values of R1, R2, C1, and C2 can be obtained by curve fitting of experimental data. The double exponential fitting method is used in the parameter identification of the improved PNGV model. During a period of standing after the discharge, the circuit current value is zero and the RC circuit has no input [8]. The above parameters are relatively simple to obtain by fitting the voltage curve of this section. Therefore, this curve is selected for fitting to obtain the above parameters. According to the circuit principle, the output equation of the battery terminal voltage can be obtained [9]. Let τ1 represents the time constant of the parallel circuit of R1 and C1, τ2 represents the time constant of the parallel circuit of R2 and C2. In order to reduce the difficulty of parameter identification and calculation, the correlation coefficient of the equation is simplified, and the result is shown in Eq. 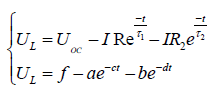(3).

(3)

To establish a simulation model to verify the accuracy of the relevant parameters, a function of the parameter with respect to the SOC needs to be obtained [10]. The function can be obtained by fitting parameters with SOC values, and the function of UOC on SOC is fitting with fifth-order polynomial. The functions of parameters R1, R2, C1, C2 and R0 on SOC are fitting with four [11]. The fifthorder fitting polynomial is shown in Eq. 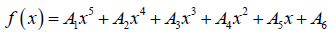(4).

(4)

In Eq. (4), the independent variable x represents the SOC value, the dependent variable f(x) represents the parameter to be fitted UOC, A1~A6 are polynomial undetermined coefficients.

Experimental analysis

c. Parameter identification

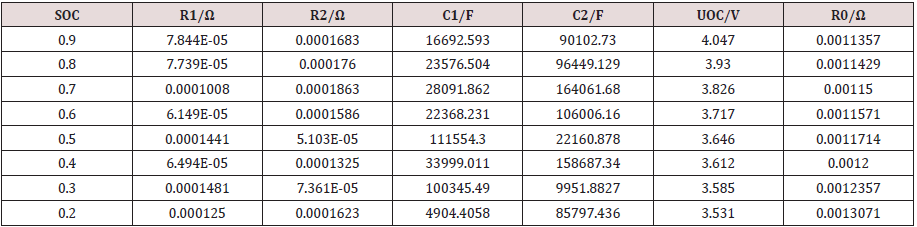
Process the result data obtained from the HPPC experiment, calculate the battery ohmic resistance value under different SOC values from Eq. (2), and then use Eq. (3) as the target formula to fit the relevant data. The identification results are shown in (Table1).

From the results shown in (Table 1), it can be seen that as the battery capacity decreases, the internal resistance of the battery will continue to increase non-linearly. When the discharge is about to end, the amount of change in internal resistance increases. The SOC of the lithium battery has a great influence on the parameters of the equivalent model, and each parameter has a huge change in different SOC values.

d. Simulation model establishment and parameter identification

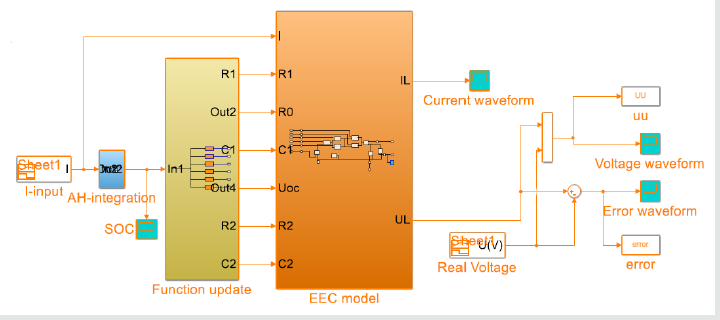
The simulation circuit of the improved PNGV model is established. In the model, the SOC update link is mainly used to calculate the SOC value at different times through ampere-hour integration. The parameter update link is used to input the function of the parameter on the SOC [12]. The model voltage output link is used to output the simulation voltage. The simulation model is shown in [Figure 3].

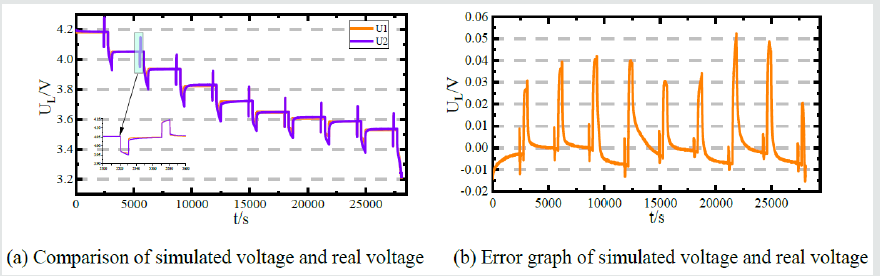
Extract the charge and discharge current values and the battery terminal voltage values in the experimental results of the HPPC characteristics, and import them into the simulation model input module, and then import the function into the update module [13]. Carry on the simulation experiment to the model, the simulation result is shown in [Figure 4]

In [Figure 4], U1 represents the actual voltage, U2 represents the simulated voltage. Due to the influence of measurement deviation and environmental factors, when the current pulse arrives, the terminal voltage of the battery will change dramatically, and then the error between the experimental value and the simulation value will increase. When the battery discharge is about to end, the violent chemical reaction inside the battery causes the parameter values. The change has caused the error between the simulated voltage and the actual voltage to increase. The overall system error is less than 0.01V, and the system parameter identification accuracy is high

Conclusion

In order to describe the dynamic and static characteristics of lithium batteries better, the traditional PNGV model has been improved. The double exponential fitting method was applied in parameter identification to simplify the calculation. The verification results shown that the improved PNGV model has a simple circuit structure and a better simulation effect. The double exponential fitting method greatly reduced the difficulty of model parameter calculation and improved the accuracy of parameter identification. The establishment of the improved model and the use of the double exponential fitting method solved the problem of insufficient accuracy of the battery simulation model and large amount of calculation for parameter identification. It created conditions for the research of SOC estimation.

Acknowledgments

The work was supported by National Natural Science Foundation of China (No. 61801407), Sichuan science and technology program (No. 2019YFG0427), China Scholarship Council (No. 201908515099) and Fund of Robot Technology Used for Special Environment Key Laboratory of Sichuan Province (No. 18kftk03).

References

1. Chen, Han Sun, GuangzhongDong, JingwenWei,JiWu, et al. (2019) Particle filter-based state-of-charge estimation and remaining-dischargeable-time prediction method for lithium-ion batteries. Journal of Power Sources 414: 158-166.
2. Tang XP, FurongGao, ChangfuZou, KeYao, Wengui Hu, et al. (2019) Load-responsive model switching estimation for state of charge of lithium-ion batteries. Applied Energy 238: 423-434.
3. Chen ZW, LiwenYang, XiaobingZhao, YourenWang, ZhijiaHe et al. (2019) Online state of charge estimation of Li-ion battery based on an improved unscented Kalman filter approach. Applied Mathematical Modelling 70: 532-544.
4. Wang HY, Chen Chen, Tao Tao, Zeyu Qiao, Youyou Fan, et al. (2019) Novel estimation solution on lithium-ion battery state of charge with current-free detection algorithm. Iet Circuits Devices & Systems 13(2): 245-250.
5. Shen JN, Jia-Jin Shen, Yi-Jun He, Zi-Feng Ma (2019) Accurate State of Charge Estimation With Model Mismatch for Li-Ion Batteries: A Joint Moving Horizon Estimation Approach. Ieee Transactions on Power Electronics 34(5): 4329-4342.
6. Ouyang M, Xin Lai, Wenkai Gao, Li Jianqiu, Long Zhou, et al. (2019) A comparative study of global optimization methods for parameter identification of different equivalent circuit models for Li-ion batteries. Electrochimica Acta 295: 1057-1066.
7. Gou Y, Han X (2018) Study of SOC dynamic estimation method of power lithium battery. IOP Conference Series: Materials Science and Engineering 452(3): 032057.
8. Liu X, Chaoyi Zheng, Ji Wu, Jinhao Meng, Daniel-Ioan Stroe, et al. (2020) An Improved State of Charge and State of Power Estimation Method Based on Genetic Particle Filter for Lithium-ion Batteries. Energies 13(2): pp. 478.
9. Li J, Liu M (2019) State-of-charge estimation of lithium-ion batteries using composite multi-dimensional features and a neural network. IET Power Electronics 12(6): 1470-1478.
10. Li K, Boon-Hee Soong, King Jet Tseng, Feng Wei (2018) et al. A Practical Lithium-Ion Battery Model for State of Energy and Voltage Responses Prediction Incorporating Temperature and Ageing Effects. IEEE Transactions on Industrial Electronics 65(8): 6696-6708.
11. Wei X, Yimin M, Feng Z (2019) Lithium-ion Battery Modeling and State of Charge Estimation. Integrated Ferroelectrics 200(1): 59-72.
12. Schaltz E, SS Madani, SK Kaer (2018) A Review of Different Electric Equivalent Circuit Models and Parameter Identification Methods of Lithium-Ion Batteries 87(1): 23-37.
13. Smirnov MA, Fedotov IV, Moiseev SA, et al. (2019) Analysis of the charge state of nitrogen-vacancy centers in diamond driven by an infrared laser field. Journal of Physics: Conference Series 1410(1): 012143.