Lupine Publishers Group
Lupine Publishers
Menu
ISSN: 2641-1687
Research Article(ISSN: 2641-1687) 
Accommodated Tonic Detrusor Pressure Determined by The Combination of Variable Elastic Volume and Variable Elastic Compliance Explained by Means of Sliding Filaments Model Volume 4 - Issue 1
Wim A van Duyl1,2*
- 1Formerly at Department of Medical Physics and Technology, Erasmus University Rotterdam, Netherlands
- 2Department of Electronic Instrumentation Technical University Delft, Netherlands
Received: December 13, 2022; Published: December 19, 2022
Corresponding author: Wim A. van Duyl, Formerly at Department of Medical Physics and Technology Erasmus University Rotterdam and at Department of Electronic Instrumentation Technical University Delft, Netherlands
DOI: 10.32474/JUNS.2022.04.000176
Abstract
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
Purpose: Experimental observations in a previous study have revealed that detrusor pressure accommodated to volume is not determined by total volume but by the combination of elastic volume and elastic compliance. In this article is looked for an explanation of this remarkable phenomenon by means of a new concept for the interpretation of the cystometry of the passive and the active bladder.
Method: Consideration of experimental data of elastic volume VE, elastic compliance CE and detrusor pressure pd in a state of equilibrium between elasticity and plasticity of pig bladder ex-vivo in relation to sliding filaments model of smooth muscle cells.
Results: Strain and contraction history affect the equilibrium condition of a passive accommodated bladder and the contractility of stimulated bladder. The observed combined variation of elastic volume VE and elastic compliance CE can be explained by variation of a distribution function n(h) which reflects the elastic elongated condition of the smooth muscle cells in a network. In the development of pressure of an isovolumetric stimulated bladder elastic volume VE is constant.
Conclusion: Bladder mechanics is more complicated than is assumed by the usual interpretation of slow filling cystometry and of isovolumetric contractility measurement in-vivo. A certain detrusor pressure accommodated to a certain volume can be obtained by different values of the ratio: elastic volume VE/rest volume VR. This property is masked in standard cystometrograms. Mechanics of the bladder are complicated because the elongated states of the actomyosin units, distributed in a network of smooth muscle cells, are different and varying. Observed variation of VE and CE is related to the variations in the distribution function n(h) of the elastic elongated states of the actomyosin units. History of strain and contraction and of spontaneous micromotions of the bladder affects rest volume VR and consequently the distribution function n(h). It has been hypothesized that the actual elastic volume VE of an isovolumetric not-stimulated bladder just before stimulation, is maintained during stimulation.
Keywords: Urinary bladder; elastic compliance; spontaneous contractions; strain and contraction history; actomyosin unit
Abbreviations
C-Compliance parameter
CE-Elastic compliance
CE-Contractile element in Hill’s model
F-Force
h-Elastic elongation of a chain of cells
hmax-Maximum elastic elongation chain of cells
n-Number of chains
n(h,t)-Distribution function of elastic elongations of chains of cells
np (h,t)-Distribution function of elastic elongations of chains of cells of passive bladder
na (h,t)-Distribution function of elastic elongations of chains of cells of activated bladder
PCE-Plasto/contractile element in van Duyl’s model
pd-Detrusor pressure generated by stress in the wall
pdp-Passive detrusor pressure
pda-Active detrusor pressure
pdt-Tonic component of detrusor pressure
pdw-Wavy component of detrusor pressure
Δ-Change in a variable
ΔlE-Elastic elongation
SEE-Serie elastic element
t-Time
v-Velocity of shortening
V-Bladder Volume
VE-Elastic volume
VR-Rest volume
Vr-Residual volume
Introduction
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
During physiological filling of the bladder and in clinical slowfilling cystometry (<1 ml/s) detrusor pressure pd is low and the graph of pressure pd-vs-volume V, with pd in the range of e.g., 5-10 cm H2O for V in the range of 100 to 400 ml, has a small almost linear upwards slope. The ratio of a volume change ΔV and associated change in detrusor pressure Δpd is defined as compliance: C= ΔV/ Δpd. In cystometry compliance is evaluated as a clinical parameter to judge the reservoir function of the bladder. In humans the normal compliance, as defined by ICS-Standardizing Committee [1], is in the range of 20-40 ml/cm H2O. Also, steepness of the upwards slope of the cystometrogram Δpd/ΔV, which is equal to the reciprocal value of C, is clinically also taken as a measure of compliance. In this article compliance C that is derived from steepness of cystometrogram will be referred to as cystometrographic compliance. A linear upwards slope of the cystometrogram means that cystometrographic compliance is a constant. Determination and clinical meaning of bladder compliance is still questionable [2].
In particular the value of differential ratio ΔV/Δpd depends on the rate of applied volume change dV/dt: the higher the rate of filling of the bladder the lower is ratio ΔV/Δpd [3]. It is supposed that in slow filling cystometry filling rate is low enough to obtain a continued visco-elastic accommodated state of detrusor pressure to the increasing volume. If ΔV is applied as fast as possible, ideally stepwise, then this causes an upwards step Δpd in pressure. This step response to pressure is ascribed to elasticity of bladder wall. Therefore, we define the differential ratio ΔV/Δpd derived from a step response as elastic compliance CE [4]. An upwards step in pressure, caused by a stepwise increase in volume, is followed by a gradual pressure decay, denoted as pressure relaxation, which ends at a higher steady pressure level than before the stepwise increase of volume. In a similar way, a downwards step in pressure -Δpd, caused by a stepwise decrease in volume -ΔV, is followed by a gradual pressure increase, denoted as pressure recovery, which ends at a higher steady pressure level. Pressure relaxation is ascribed to passive properties of bladder tissue and pressure recovery is ascribed to active properties of the contractile component of bladder tissue.
Commonly the clinical determination of bladder compliance is limited to non-activated bladders and the determination of clinical bladder contractility is limited to activated bladders. We concentrate on the mechanical properties of the bladder and exclude effects of central nervous system on the mechanical state of a bladder by studying the bladder ex-vivo. Mechanical characteristics of the bladder in the collection phase, in particular concerning the relation of detrusor pressure pdp to volume V, are supposed to be dominated by the passive properties of bladder tissue and characteristics of the bladder in the evacuation phase, in particular detrusor pressure pda related to volume V, are supposed to be dominated by the active mechanical properties of the muscular tissue component. The amount of volume ΔV that needs to be withdrawn stepwise out of a bladder with volume V to obtain just zero detrusor pressure has been defined as the elastic volume VE of the bladder [4]. Such a quick release of the elastic elongated state can be applied on a passive, non-activated bladder and on an activated bladder. If within a certain range of V, the elastic compliance CE = ΔV/Δpdt is a constant, then also holds CE = VE/pdt. The step-in pressure from an accommodated level to zero level of a not-activated bladder is equal to the actual value of the steady or tonic detrusor pdt.
The remaining volume, after withdrawal of the elastic volume VE out of the bladder, is denoted as rest volume VR of the bladder, so that V=VE+VR. Rest volume VR of a not-activated bladder is determined by the circumferential rest length of tissue strips as part of the bladder, if the bladder is approximated as a sphere. It is relevant to note that because VR is part of V, detrusor pressure pd is not determined by total bladder volume V but by its part VE. During the physiological collection phase or during artificial slow filling of the bladder, starting from rest volume VR, the gradual pressure increase is caused by the increase only of elastic volume VE, in combination with the actual value of CE. The intravesical pressure built up during filling from V=0 till V=VR is caused only by the increasing hydrostatic pressure in the bladder and this pressure increase is accompanied by a heterogeneously distributed elastic elongation of the bladder wall. For V>VR a more homogeneously distributed component of elastic elongation is added, developed by enclosing the volume V that is larger than rest volume VR.
Usually in clinical cystometry rest volume VR is not considered as a variable parameter, either VR is implicitly assumed to be constant. Increasing the volume of the bladder implies thinning of bladder wall. Consequently, for a constant elastic compliance CE, with reference to a constant rest volume VR, the stiffness of the elasticity of tissue of circumferential strips with constant rest length, needs to increase progressively with the elongated length. Such a progressive stiffness of elasticity of bladder tissue has been confirmed experimentally on tissue strips [5]. Minimal rest volume of the bladder is obtained after a completed micturition. Clinically this smallest rest volume is called residual volume Vr. Normally residual volume Vr is almost zero. Rest volume VR normally is normally is considerably larger than residual volume VR: VR>Vr. Circumferential length of the bladder needs to be considerably reduced to enclose the small size of residual volume Vr after micturition. When rest volume VR is reduced by the activation of contractile tissue, eventually enclosing zero residual volume Vr , then its wall is still composed of all contractile tissue and all elastic tissue. However, because circumferential rest length is reduced by contraction, rest length of elastic tissue is part of total rest length. Hence bladder wall is characterized by contractile and elastic tissue in series.
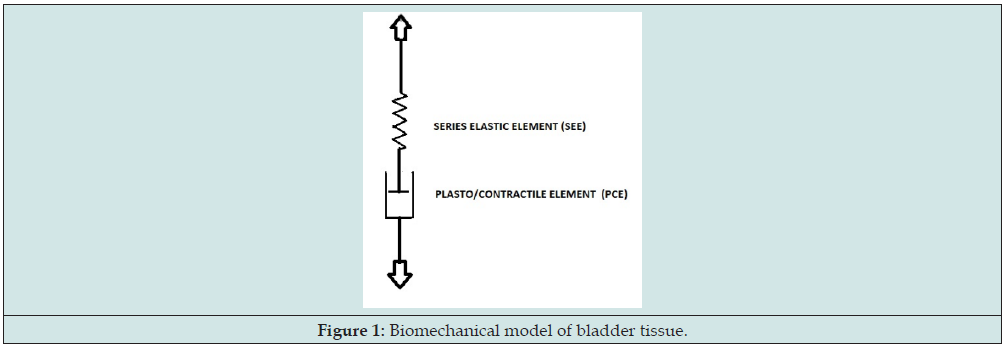
It has been observed that rest length of not-activated pig bladder strips also is variable [6]. This variation of rest length has been ascribed to plasticity of bladder tissue. Only when a certain threshold value of tension across the strip is passed, a certain increase of rest length of the strip is obtained. The higher is the previously attained plastic elongated state of a strip, the higher is the threshold which needs to be passed to get more plastic elongation. Because of this plastic property of bladder wall a tonic detrusor pressure pdt can be maintained by the combination in series of plastic and elastic tissue. Phenomenologically passive plastic elongation and active muscular contraction can be considered as antagonistic processes in tissue strips [7]. To account for these antagonistic effects on the actual length of a tissue strip or of a circumferential strip as part of bladder wall, a plasto/contractile element PCE has been introduced, shown in Figure 1. In the mechanical model of Figure 1 all elasticity distributed in bladder wall is represented by element SEE. This means that in a strip, that is fixed at a certain length, the elongated state of both elements is variable, but set by attained plastic elongation and by stimulated or spontaneous contractions. According to this mechanical model the tonic detrusor pressure pdt at a certain volume V also is a state of equilibrium between the actual length of PCE and the elongated state of SEE of tissue of bladder wall. By means of the model of Figure 1 the mechanics of passive, activated and spontaneous active bladder can be described [8,9].
In this way passive and active bladder mechanics is considered by separating the conditions of just two different tissue components, represented by the two biomechanical elements SEE and PCE, which correspond to the separation of total bladder volume V in respectively elastic volume VE and rest volume VR. According to this model the elastic compliance CE is determined by the characteristic parameters of SEE. The difference of elastic compliance of a passive and of active bladder tissue is expressed in differences in the characteristics of SEE. The property of increasing threshold for plastic elongation with increasing elongated state of PCE is taken as a particular characteristic parameter of PCE. Gradual slowly straining of a strip of tissue is accompanied by lengthening, but partly by elastic lengthening of SEE and partly by plastic lengthening of PCE. The progressive stress in bladder wall with increasing bladder volume, generated by elasticity with progressive stiffness of SEE, needs to be withstood by the threshold of PCE for plastic elongation. Therefore, we expect, for a not-activated bladder with certain parameter values of SEE and PCE, that the attained maximum value of elastic volume VE and attained value of rest volume VR are related. In the clinical contractility measurements, it is intended to evaluate the characteristics of the activated PCE and this time in particular to evaluate the velocity of shortening v of the activated PCE. Provided that the characteristics of SEE of bladder wall are known, the velocity of shortening of activated PCE of bladder wall can be derived from the increase of detrusor pressure of a stimulated isovolumetric bladder. This was the basis of an initially proposed procedure [10].
Elastic Compliance CE, Elastic Volume VEand Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
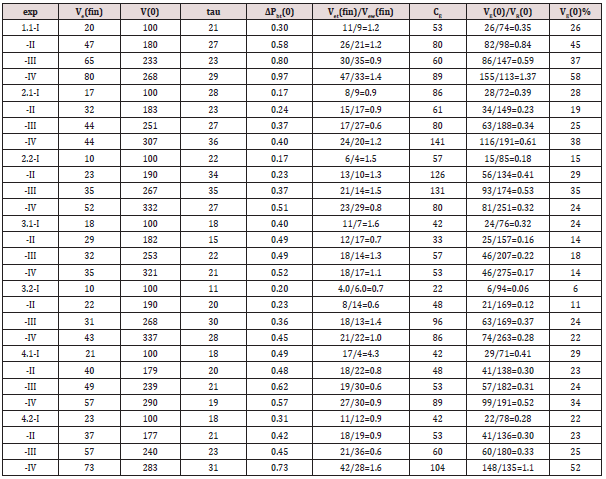
We are interested in the elastic compliance of the bladder when detrusor pressure is accommodated to a certain volume. As explained before the elastic volume VE can be determined by measuring the volume that needs to be withdrawn stepwise to reduce the accommodated detrusor pressure to zero. Because detrusor pressure of a not-activated bladder is low, the application of this procedure is tricky. An alternative method to determine CE and VE was applied, which was based on the analysis of the gradual decay of bladder pressure during autonomous driven expulsion of fluid via a known flow resistor. We shortly describe here that experimental procedure. The procedure was applied on pig bladders in-vitro, submerged in a bath of oxygenated metabolic solution at 37°C. In the experimental setup for slow emptying cystometry the hydrostatic force on the expulsion, caused by the weight of fluid in the bladder, was excluded. During each expulsion of a pig bladder the intravesical pressure p(t) and the expelled volume VE(t) were recorded. The recorded expulsions started from an initial detrusor pressure pd that was accommodated to different amounts of initial bladder volume V(0). For the considered dynamical aspects of an accommodated state we refer to [4].
The procedure on a particular bladder was subdivided into four phases (1,2,3,4). In phase 1 the bladder was filled by infusion of metabolic fluid at 37°C at a low rate of approximately 1 ml/s to initial volume V(0) = 100 ml. In phase 2 detrusor pressure was allowed to accommodate to volume V(0) for approximately 5 minutes. In phase 3 the initial detrusor pressure started an autonomous expulsion, limited by a low hydrostatic pressure in the collection reservoir of expelled volume. In phase 4 equilibrium of hydrodynamic pressure between bladder and the collection reservoir was re-instated. After phase 4 an amount of 100 ml was added to the remaining volume of the bladder after a previous expulsion, so that the following expulsion started at an initial volume V(0) that is larger than at the start of previous expulsion. In this way four successive expulsions (I,II,III,IV), each consisting of four phases (1,2,3,4), were recorded on each bladder with successively larger initial volume V(0). In this procedure the initial values of detrusor pressure pd and volume V(0) at the start of each expulsion can be taken to correspond to a point of a slow filling cystometrogram that otherwise could have been made of the bladder.
The four points (pd, V(0)), concerning different initial conditions and supposed to correspond to four points of a hypothetical slow filling cystometrogram, are illustrated in Figure 2. For more experimental details and for the mathematical analysis of the data we refer to [4] Figure 3 is an example of the recording during an autonomic expulsion of the decaying pressure and of the simultaneously increasing amount of expelled volume Ve(t) gathered in the collection reservoir (exp.nr.4.2-III). Both recordings in this Figure eventually end at a steady level. In the experiments all recordings of detrusor pressure show transient waves, like in Figure 3. Similar pressure waves are seen in clinical cystometrograms and are ascribed to spontaneously generated contractions in bladder wall. Such spontaneous contraction waves may be associated with urological complaints. Recently spontaneous activity has been ascribing also a physiological role in the accommodation of detrusor pressure to volume [9]. Commonly the transient pressure waves pdw are considered to be superimposed on tonic pressure component pdt. In the pressure recordings the decaying tonic component pdt has been defined by the lowest pressure values attained after the transient waves, which are fit to the tonic pressure, in Figure 3 marked by numbers.
Figure 2: Illustration of four autonomous expulsions starting from initial accommodated condition of pd to V(0) corresponding to points of a hypothetical cystometrogram.
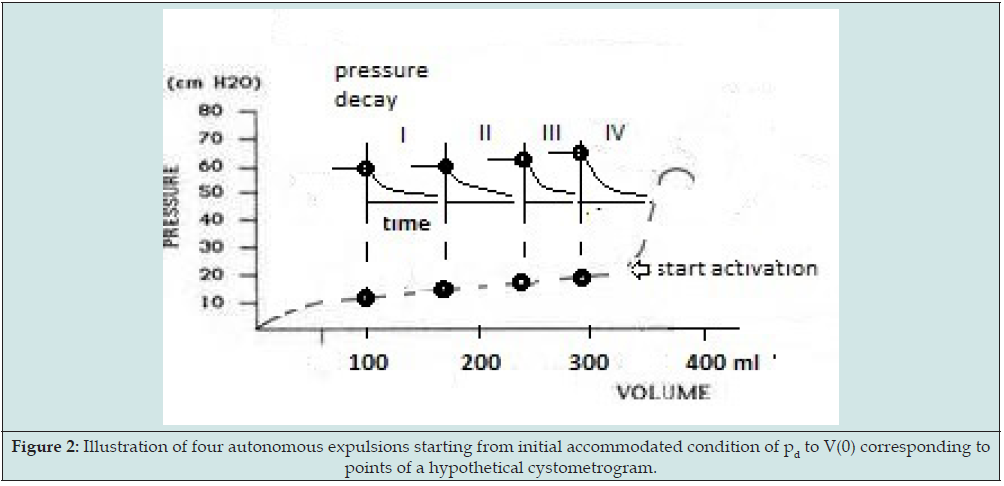
Figure 3: Example of recording (phase 3 of expulsion III of exp. nr. 4.3) of bladder pressure p(t) (upper recording) and of expelled volume Ve(t) (lower recording). In the upper recording the smooth curve is the fitted mono-exponential component representing decaying tonic pressure.
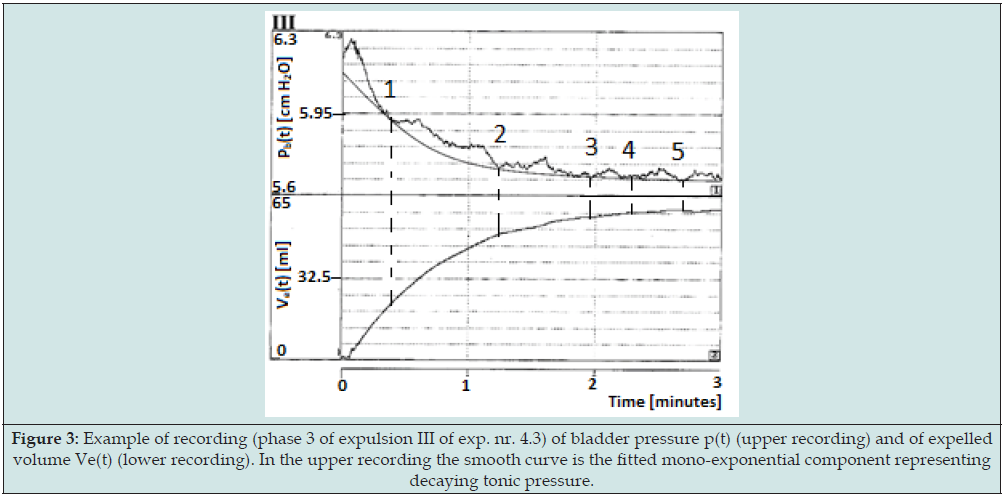
The separated tonic pressure components could be fitted by a mono-exponentially decaying function determined by a certain time constant (tau). In Figure 3 it is the fitted mono-exponential function that has been added to the recording. The mono-exponential function has been ascribed to the expulsion of the bladder by elasticity of bladder wall. From the fitted time constant the value of CE has been calculated. Obviously during an expulsion, the elastic compliance CE is constant. In most recordings of detrusor pressure pd(t) the spontaneously generated contraction waves pdw(t) are completely transient and clearly separable from tonic detrusor pressure component pdt(t). Sometimes, however, spontaneous contraction activity is accompanied by an increasing tonic detrusor pressure level. This indicates that, despite the applied separation, spontaneous activity and tonic pressure somehow have become interrelated. Spontaneous increase of isotonic detrusor pressure may be taken a particular type of bladder instability and be a cause of incontinence.
Summary of Published Experimental Results
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
We recapitulate remarkable results of the expulsion experiments in order to give finally an explanation in terms of a sliding filaments model of bladder tissue. Figure 4 is a graphic representation of the values of the elastic compliance CE taken from Table 1 in [4]. By multiplying CE with the initial amplitude of tonic detrusor pressure pdt(0) the values of the elastic volume VE(0) at the start of an expulsion were derived: VE(0) = CE.pdt(0). Figure 5 is a graphic representation of the values VE(0), also taken from Table 1. Each point in the graphs of Figures 4 & 5 refers to the result of an expulsion from a certain initial volume V(0) plotted along the horizontal axis. In the expulsion experiments VE(0) varied in the range of 10-55% of V(0). Subtraction of elastic volume VE(0) from initial volume V(0) yields the initial value of rest volume VR(0): V(0) -VE(0)= VR(0). Hence variation of VR(0) was in the range of 90- 45% of V(0). Between separate expulsions ratio VE(0)/VR(0) varied between 0.1 and 0.8.
Figure 4: Variation of elastic compliance CE with increasing initial bladder volume V(0) derived from elastic expulsions.
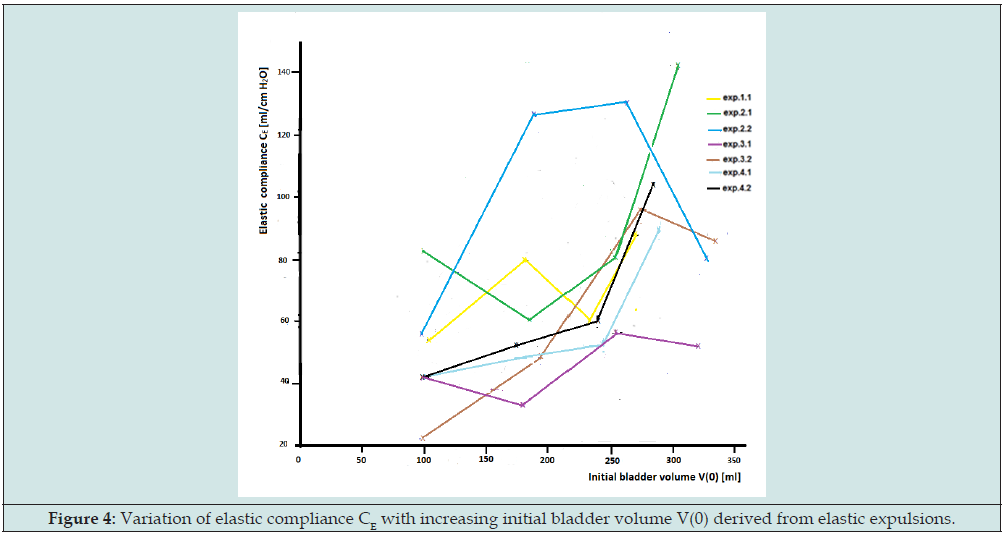
Figure 5: Variation of elastic volume VE(0) with increasing initial bladder volume V(0) derived from elastic expulsions.

Figure 4 shows that the series of expulsions I,II,III,IV illustrated in Figure 2 yields values of elastic compliance with large variations. Yet the initial accommodated detrusor pressure before each expulsion is in the small range of accommodated detrusor pressure as could be found in a slow filling cystometry. The large variation in CE is not observed in a similar large variation in detrusor pressure Δpdt , because in Δpdt = ΔVE/CE the effect of variation in CE on Δpdt is reduced by a similar change in elastic volume ΔVE , shown in Figure 5. The expulsion experiments have revealed that a certain accommodated detrusor pressure pdt can be attained by equilibrium with different values of ratio VE/VR. After each expulsion final rest volume VR(fin) can be derived by subtraction of elastic volume VE from measured final total amount of expelled volume Ve(fin): VR(fin) = Ve(fin)-VE. If fluid were expelled only by the elasticity of bladder wall, then the final rest volume VR(fin) would be equal to initial rest volume VR(0).
It turned out, however, that in all cases the finally expelled volume Ve(fin) is larger than the calculated amount expelled by the elasticity that generates the tonic component, so always: VR(fin) < VR(0). The extra amount of fluid is expelled by the pressure waves pdw (t) superimposed on the tonic pressure pdt(t). Of course, this extra amount varies because spontaneous contraction activity in bladder wall varies. In the experiments the ratio of the volume finally expelled by the tonic component Vet(fin) and the volume finally expelled by the wavy component Vew(fin), Vet(fin)/ Vew(fin), varied between 0.5 and 1.5. Hence the amount expelled by spontaneous activity is relatively considerable. The volume expelled by the pressure waves equals the reduction of rest volume VR during expulsion. In terms of the model of Figure 1, during an autonomous expulsion bladder, volume V is reduced by the reduction of elastic elongated state of SEE and simultaneously extra reduced by spontaneous contraction of the plastic state of PCE.
Mechanical Explanation
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
Strain and contraction history of bladder wall by repeated emptying and refilling of the bladder in each series of four expulsion experiments on a bladder is different from history of strain by continuing slow filling in standard cystometry. Next, we consider this difference in history as the cause of the observed variation in CE and in the accommodated state expressed in variation of VE/VR. Although Figure 4 shows that CE varies in successive expulsions, CE appears to be constant during an autonomous expulsion. It can be proven theoretically that a bladder having elasticity with a certain value of stiffness that is progressive with elongation, referred to constant circumferential rest length, has a constant elastic compliance within a limited range of volume [11]. The assumption of a constant rest length of SEE as a parameter contradicts the observation that during autonomous expulsion circumferential rest length decreases by reduction of plastic elongated state of PCE caused by spontaneous contractions. So, we need to look for another explanation for the constant CE during the expulsions. The assumption of constant parameters of elasticity is also in contrast to the phenomenon of “strain softening” [12].
When a strip of bladder tissue is released after been strained by a certain force and restrained to a length equal to the length in previous straining, then in the second case the needed force is smaller than before. This reducing effect of repeated strain on elasticity is called “strain softening”. The increased values of CE in the series of expulsion experiments may be caused by “strain softening” after refilling of the bladder to a larger volume. According to our model of Figure 1, we need however to distinguish in the results of “strain softening” change of stiffness of SEE from increase of plastic elongated state of PCE. Moreover, the graphs of Figure 4 also show large decreased values of CE with increasing volume V. If a decrease of stiffness is supposed to be caused also by strain history of the bladder, then we may speak also of an effect of “strain stiffening”. Besides considering the effects of straining history on CE, we also consider effects of spontaneous contraction activity on CE. The effect of spontaneous contraction activity on elasticity has been studied separately on pig bladder strips [13].
The results of stress-strain measurements on strips, submerged in a Krebs solution, have been compared with the results obtained on strips submerged in a Ca-free EGTA solution that suppresses contractile activity. Because of the large statistical variations in the fitted parameters no significant difference was detected in the elasticity parameters that could be ascribed exclusively to suppression of spontaneous contractile activity. So, these results do not contradict our observation that transient pressure waves, superimposed on tonic pressure during the expulsions, show no significant effect on the value of elastic compliance. The observed maintenance of a certain value of elastic compliance during an autonomous expulsion, despite reduction of rest length by spontaneous contraction activity, concerns a particular manifestation of bladder wall that has been ascribed to the localized nature of the transient spontaneous contractions [14]. The expulsion experiments have shown that small regions with completely transient contractions return to the elastic elongated state that is determined by the actual dominating tonic pressure component [4].
So, for completely transient spontaneous pressure waves the local increased stiffness also is completely transient and does not affect the course of elastic expulsion, although the spontaneous localized contractions decrease during expulsion rest volume. In contrast to completely transient waves of localized spontaneous contractions, stimulated steady contractions evidently have a large effect on elastic compliance. Increase of stiffness has also been observed on stimulated strips of pig bladder. Isometrically fixed strips have been electrically stimulated to contract, while the development of activated force F(t) across the strip has been recorded. Quick release of length with ΔlE of the activated strip, needed just to attain zero force and starting such a release from different levels of developing force F(t), has been measured. The remarkable result is that the needed quick release of ΔlE appears to be independent of the developed level of force F(t) [14]. Between separate experiments the needed ΔlE varies however considerably, between 4.5-20.5 % of the initial length of different strips. Of course, we ascribe force F(t) across a strip to the elongated state of SEE in Figure 1.
The quick release studies indicate that during development of F(t) the elongated state of SEE does not change but stiffness of SEE increases. In other words, the more the activated state has developed, the stiffer is SEE. The needed quick releases of ΔlE of activated strips has been studied also on previously strained strips [15]. That study revealed that ΔlE is composed of two parts. The main part of ΔlE still is the part of elastic elongation that is independent on the level of activated force F(t). The other part depends on force across the strip and is ascribed to elasticity of connective tissue and is not affected by activation. In the model of Figure 1 both forcedependent and force-independent parts of elasticity can be ascribed to the characteristics of SEE. The value of the force-independent part of ΔlE increases almost linearly with the strained state of the strip. We conclude from these quick release studies on stimulated pig bladder trips that ΔlE may vary considerably but is a constant of a particular strip during its development of isometric force.
In terms of total bladder this conclusion means that the development of detrusor pressure of an activated isovolumetric bladder is accompanied by reduction of CE and not by increasing of VE. Obviously during development of stress in bladder wall, there is a certain value of ΔlE concerning the elastic part of circumference that is not affected by stimulation. Earlier we stated that the elastic elongated state and plastic elongated state of a not-stimulated bladder, previous to stimulation, depend on properties which are determined by strain and contraction history of bladder wall. Now we hypothesize that the observed maintained value of ΔlE of a stimulated isometrical fixed strip even corresponds to the previous existing elastic elongated state of the passive strip. In other words, the hypothesis is that during transition of an isovolumetric bladder from passive state to activated state the elastic volume VE of passive bladder is supposed to be maintained, while CE reduces.
When we translate the observed variation in ΔlE of 4.5-20.5% of the initial length of a strip to an equivalent variation of elastic volume VE of an isovolumetric activated bladder with total volume V, then we get an equivalent variation of approximately 13-50% of total volume V. This range of equivalent variation in VE is about equal to the range of variation of elastic volume we experimentally have found for an accommodated not-stimulated bladder in the expulsion experiments, being 10-50% of volume V between 100 and 300 ml in Figure 4. These almost equal ranges of variation in VE strengthen our hypothesis that the maintained elastic volume VE during isovolumetric stimulation is equal to the VE of the passive bladder just before stimulation. Based on this hypothesis it has been suggested to evaluate VE during isovolumetric contraction of a bladder in-situ as a clinical experimental parameter [16]. Electrical stimulated contractions have an increasing effect on stiffness. Contractions are also stimulated by straining of bladder wall.
Such myogenic induced contractions may also increase stiffness during phase 1 of refilling of the bladder in the expulsion experiments and may contribute to variation in CE. The conclusion, drawn from the expulsion experiments and from the quick release experiments, that the characteristics of SEE are variable and depend on strain and contraction history and on contracted state of a bladder, have of course undermined the validity of earlier, though sometimes still recommended clinical contractility measurements, which are based on the development of detrusor pressure during stimulated isovolumetric contractions [17]. Because spontaneous contraction activity and micromotions may be regional and migrating and because of the history of strain and contraction, the mechanical state of bladder wall is not constant but dynamic and heterogenous. To imply heterogeneity of the mechanical state in our explanation of the experimental results of the expulsion experiments, we need a more detailed consideration of bladder smooth muscle.
Application of The Sliding Filaments Model
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
Since the publication about contraction of striated muscle by Huxley in 1957, based on overlapping myosin and actin filaments which can slide along each other by the kinetics of cyclical generated cross-bridges between the filaments [18], many authors have presented measurements indicating that the filaments contribute variable components to the stiffness of elasticity of muscular tissue. Mechanical experiments, similar to those on tissue strips of smooth muscle, have been performed on single smooth muscle cells [19,20]. Kinetics of cross-bridges have been studied also on smooth muscle. Within a smooth muscle cell bundles of filaments make up a micro network anchored with dense bodies to the cell membrane, Figure 6A. Myosin filaments and thinner actin filaments forming an actomyosin unit in a cell can slide along each other, Figure 6B. Myosin filaments can become attached to actin filaments by bridges, Figure 6C. Myosin and actin filaments which are not attached to each other can freely slide along each other. If filaments are attached by bridges, a force can elongate an actomyosin unit by resistant passive slippage of the filaments along each other, or an actomyosin unit can shorten by slippage in the direction of the opposing force due to the kinetics of bridges.
The kinetic of a bridge is a cyclic process of attachment, detachment and re-attachment by heads of the myosin filaments to the surrounding bundle of actin filaments. During this cycling process the heads of myosin filaments are bending, so that when attached they move along the actin filament. Force across a cell causes elastic elongation of the structure within the cell in the direction of the force and in particular causes elastic elongation of the inside filaments. Stiffness of elasticity of a particular actomyosin unit depends on the number of attachments between the filaments. This implies that stiffness of an actomyosin unit is not a fixed characteristic. In a similar way stiffness of a strip of smooth muscle is not a fixed characteristic parameter of the tissue but depends on the attached filaments in the smooth muscle cells of that strip. The stiffness of a strip of tissue is larger if the number of fixed bridges is higher. Within the network of cells in bladder wall the ratio of attached and not-attached filaments of actomyosin units is variable. In smooth muscle cells two types of attached states between the filaments have been distinguished: weak binding and strong binding attachments [21].
Weak binding bridges resist a lower force across the actomyosin unit than strong binding bridges. Strong binding bridges are generated during an activated contraction. Transition of an attached state of bridges to a detached state needs the involvement of Ca2+. The availability of Ca2+ dependents on a process of phosphorylation. Attached de-phosphorylated bridges keep attached to a location on an actine filament by weak binding. These weak binding attachments are called latch-bridges [22], see Figure 6C. Recruitment of the stronger cross-bridges in actomyosin units is initiated upon a transient increase of Ca2+ in plasma concentration, that also triggers release of Ca2+ stored in sarcoplasmic reticulum. Hence Ca2+ is the physiological activator for the dynamics of a contraction of an actomyosin unit, hence for muscular contractility. The sensitivity of an actomyosin unit for Ca2+ to generate force is a variable that depends on the mechanical state of the bridges in the unit. If the velocity of shortening of an activated actomyosin unit is mechanically limited, then the stimulated contraction generates a force that is higher for a lower allowed velocity and this force is at a maximum when zero velocity is allowed.
Figure 6: Smooth muscle cell with bundles of actomyosin units and sliding filaments model in actomyosin unit (modified after Squide).

Generally, the activated force generated by cross-bridges is considerably higher than the force that can be resisted by the notstimulated actomyosin unit with latch-bridges. Three muscular layers can be distinguished in bladder wall by their shape and orientation. The thickest middle layer of circular shaped cells is sandwiched between an inner and outer smaller layer of longitudinal oriented cells [23]. Each smooth muscle cell has a constant volume, so that a cell cannot elongate in all directions. This means that in an elongated bladder wall the smooth muscle cells are elongated in limited directions, accompanied by a passive compression in transversal directions. When a layer elongates the cells in it flatten. Flattening of cells causes compression of actomyosin units and consequently a decrease of the distance between the filaments, as illustrated by arrows in Figure 6B. Probably a decrease of distance between filaments increases the sensitivity of the actomyosin unit for Ca2+ and makes the sensitivity of a actomyosin unit dependent on its compressed state. This may explain that generated stress in the wall of a stimulated bladder is higher for more compressed bladder wall, hence for larger bladder volume.
This adaptation of activated stress response to bladder volume determines pressure-volume relation of stimulated bladders, similar to the well-known Frank-Starling mechanism of the heart [24]. A similar adaptation of stress to volume exists for the passive bladder. The filaments of a not-stimulated actomyosin unit are attached by latch-bridges. The attached latch-bridges maintain a certain contracted or elongated state of the filaments as long as force across the unit is below a threshold level, while utilizing energy at a low level. When the weak binding force of its latchbridges is surpassed then the heads of myosin filaments slip along the actin filaments, until a certain location on the actin filament is reached where a new attachment maintains that position. The intracellular slippage of latch-bridges corresponds mechanically to the mechanical property of plastic elongation [25].
The threshold of plastic elongation of a not-stimulated bladder is higher for larger rest volume of the bladder. Hence the threshold of plastic elongation of actomyosin units, determined by fixation of the latch-bridges, also needs to be higher for a more plastic elongated state. Similar to the cross-bridges in case of activated bladder, this force of fixation by the number of latch-bridges of a passive bladder may be larger also for increased transversal compression accompanying an increased rest volume. Slippage of the filaments in the actomyosin units of cells in the network of a strip of tissue will take place mainly in the direction of the applied force across the strip. Therefore, after an elongation of a strip in a certain direction the distribution of rest lengths in the network of cells is no longer homogeneous. By filling of the bladder, the existing heterogeneity of elongations of actomyosin units in bladder wall will change. The elongated rest lengths of the actomyosin units are reset by a stimulated contraction and possibly by spontaneous contractions or micromotions.
The cyclic process of the bridges, initiated by stimulation accompanied by phosphorylation, implies a transition of existing weak binding latch-bridges to strong-binding cross-bridges. This means that the elongated states of not stimulated actomyosin units is transferred to the activated state, at least at the initial phase of activation. This also sustains our hypothesis of maintenance of elastic volume VE in the transition of the bladder from passive to activated state. Strain and contraction of an actomyosin unit can be represented also by the model of Figure 1. So, to represent a piece of smooth muscle tissue or bladder wall we can use the model of Figure 1 as elements connected in a network. By means of such a network we can represent distributed and varying local mechanical properties of muscular wall of a bladder. Such a network has been used earlier to illustrate that varying patterns of micromotions in a strip of tissue are not always seen in variation of force across the strip [9]. Here we use the network to consider consequences of the history of strain and contraction for the mechanical properties of bladder wall, in particular for CE . The network of Figure 7 is a collection of connected elements equal to Figure 1, as a model of connected smooth muscle cells in a strip of tissue.
The elements are in a certain elongated or contracted state by a force across the network in one direction. The connected elements are arranged in chains in the direction of the applied force and in the direction of our observation of mechanical reactions. In Figure 7 chains of elements are illustrated in parallel. Connections of the cells alongside a chain by surrounding connective tissue are ignored in this network model. We suppose that in a piece of tissue the force across each cell of a particular elongated chain will be equal to the force across that chain. Each chain has a certain rest length equal to the sum of the lengths of the PCE’s of the elements and has an elastic elongated state equal to the sum of elastic elongations of the SEEs of the elements. Elongation of a particular chain is resisted by plasticity and elasticity of the elements in that chain. Elongation of a strip of smooth muscle in one direction implies elongation of chains of cells parallel in that direction.
Figure 7: Network of parallel chains of elements representing mechanical properties of cells in one direction, loaded by force in one direction.
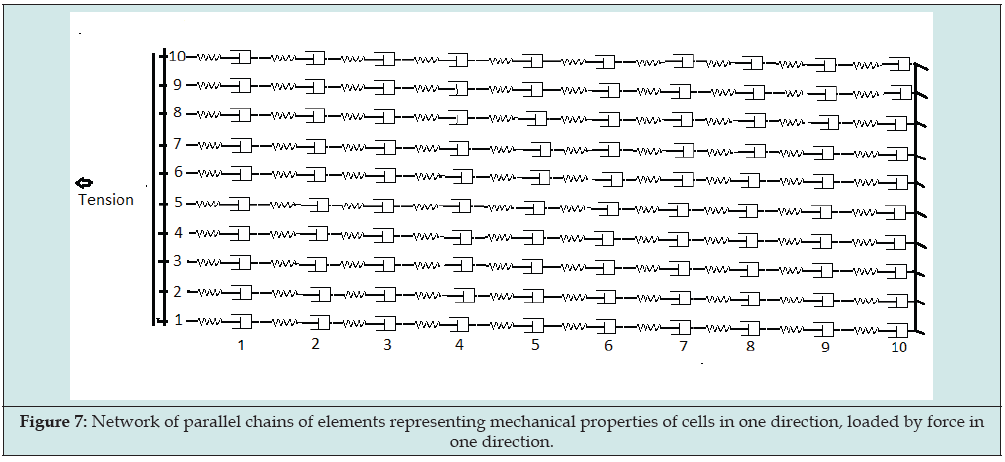
The plastic elongated part of a chain is fixed at the locations by attached latch-bridges of the actomyosin units in that chain. A higher threshold for longer plastic elongation is related to a larger number of attached latch-bridges. An increase of the number of attached latch-bridges has been ascribed to a decrease of the distance between the filaments in the actomyosin units, caused by the transversal force on the actomyosin units accompanying their elongations. Reduction of the plastic elongated state by contraction is supposed to imply reduction of the number of latch-bridges and consequently lowering of the threshold. Because the plastic elongated states of the units depend on the history of strain and contraction of a chain, the plastic elongated parts of the chains may be different. So, if a certain force is applied across a strip the elastic elongation of the chains, denoted by h, are also different. In the case of a small number of latch-bridges the elastic elongation of some chains may be almost zero. Hence the number of chains n with elastic elongation h between h = 0 and a maximum elongation h = hmax, can be represented by a distribution function, denoted by n(h). Each parallel chain contributes to overall force across the strip with a component depending on its elastic elongation h.
Change of distribution function n(h) implies change of stiffness of the elasticity of the strip. Distribution function n(h) of passive tissue np(h) will differ from distribution function na (h) of activated tissue. Ongoing contraction activity makes the distribution function n(h) a function of time: n(h,t). Changing of stiffness of the wall in any direction is built up by changing of the contributions of the chains of cells to elasticity of tissue in that direction, hence by changing of distribution function n(h,t) of the involved chains. Recruitment of latch-bridges in passive tissue or cross-bridges in activated tissue implies an increased resistance to elongation of the chains, hence implies an increased stiffness of elasticity. By means of the model of the Figure 7 we are finally able to explain the observation of changed value of CE (Figure 4) and simultaneous similar changed value of VE (Figure 5), combined so that a low and almost not changed detrusor pressure pdt is accommodated to the same volume V. Assume that recent history of straining and contraction has changed rest volume VR. When VR is smaller, then bladder wall is thicker, and as explained we expect that the number of latch-bridges is smaller and that the number of chains in n(h) which almost do not resist elongation is larger.
This means that the elastic compliance CE of the bladder is larger, so that with a certain detrusor pressure pdt the elastic volume VE is larger. This larger elastic volume is added to the smaller rest volume VR, so that total volume V can be equal to the volume without reduced VR. In a similar way we can explain that a larger rest volume VR, caused by the history of strain and contraction, implies a reduced elastic compliance CE and a smaller elastic volume VE for about the same combination of detrusor pressure pdt and total volume V. During the expulsions the elastic compliance is constant while the superimposed contraction waves cause reduction of rest volume. This seems to be in contradiction to our expectation that a decreased rest volume implies an increase of elastic compliance. Spontaneous transient varying detrusor pressure is generated by transient active cross-bridges. Then the plastic elongated states of the actomyosin units in the contracted region are reduced and the positions of the latch-bridges are adapted to the reduced state. If after a contraction wave the number of latch-bridges is not changed, then the elastic compliance is not changed and by the actual tonic pressure the latch-bridges will be slipped up to a position of shorter actomyosin units corresponding to a lower actual tonic detrusor pressure.
In other words, our explanation of the course of tonic detrusor with constant elastic compliance and reduction of rest volume by spontaneous activity is based on the exclusion that transient contraction by kinetics of cross-bridges has consequences for the shortened position of the latch-bridges but not for the number of latch-bridges. Further we conclude that release of the elastic elongation in bladder wall to zero stress at last needs the release of those chains in distribution function n(h) having the largest elongated state, hence the release of the n(hmax) strains. Quick releases have shown that during development of stress in the wall of an isovolumetric stimulated bladder a certain value of hmax of some of these chains does not change. In connection to the distribution function our hypothesis is that during transition function n(h,t) changes from np(h,t) to na(h,t), while h is maintained within the range from 0 to the maintained hmax . This corresponds to the earlier formulation of the hypothesis that during transition from passive to activated state of an isovolumetric bladder with total volume V the elastic volume VE and rest volume VR are maintained while compliance CE decreases.
Conclusion and Discussion
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
We started with defining compliance, different to Standardizing Committee, as elastic compliance CE, which relates tonic detrusor pressure pdt to elastic elongation of bladder wall, expressed by elastic volume VE as a part of total bladder volume V. With this definition we intended to ascribe the small increase of low detrusor pressure Δpdt with increasing bladder volume, in physiological filling and in slow filling cystometry, to ratio ΔVE/CE= Δpdt. However, CE appears to be not a characteristic fixed parameter of a bladder, as CE may vary considerably and the small variation of tonic detrusor pressure pdt is obtained by a simultaneous similar change of elastic volume VE. The combined variation of CE and VE, for the same volume V and detrusor pressure pdt, has been explained by a change of rest volume VR. Change of rest volume VR, caused by the history of strain and contraction of bladder wall, can change the elastic compliance CE. This makes rest volume VR a relevant variable to characterize the state of a bladder. Rest volume VR after reset of the bladder by micturition, also is relevant for the properties derived in the following cystometry.
Distribution function n(h,t), which represents the distribution of elastic elongation of filaments of actomyosin units in chains of smooth muscle cells, determines stiffness of the elastic of bladder tissue. We have distinguished distribution function hp(n,t), determined by the fixation of latch-bridges, from distribution function ha(n,t) for stimulated bladder determined by fixation of cross-bridges. It has been concluded that during isovolumetric stimulation the elastic volume VE and rest volume VR are constant, while elastic compliance CE decreases by the recruitment of cross-bridges in chain of cells. It has been hypothesized that VE of previously not-stimulated bladder and VE during isovolumetric contraction are equal. Finally, we mention some consequences of our new concept of the bladder. Colhoun et al [26] reported a reduction of stiffness of human bladder tissue from one filling to another during repeated bladder filling and passive emptying. They pointed also on the effect that stiffness is reversed after active emptying of the bladder and introduced the term “dynamic elasticity”. They have suggested that dynamic elasticity can be clinically applied as a factor for regulation to treat overactive bladder. Recently Duval et al. [27] have suggested applying the effect of “strain softening” in patients as a therapeutic non-invasive procedure to decrease bladder pressure and to increase bladder capacity.
However, according to our observations the condition of bladder wall attained by “strain softening” will be reset by a generalized contraction of the bladder during micturition, as is concluded also by Colhoun et al. So, from this point of view the procedure proposed does not offer the suggested therapeutic perspective. In case of overstrained bladder, the lost adaptation of passive and activated tonic pressure to normal bladder volume can be explained by overlap of actin and myosin filaments that is too much reduced so that these overstrained actomyosin units can be reset by contraction and rest volume VR or residual volume Vr that is larger than normal. This larger rest volume will affect the properties to be derived from cystometry. Leakage of a bladder caused by tonic pressure is comparable to the autonomous expulsions considered in this study. Our results indicate that during such a slow expulsion the elastic volume VE decreases while the elastic compliance CE may be constant. But, superimposed spontaneous contraction activity during leakage causes reduction of rest volume VR. Our Consideration of results of basic mechanical experiments, particularly obtained from autonomic expulsions of pig bladders, makes clear that compliance of passive and activated bladder reflect a much more complicated nature of the bladder than is suggested by the common interpretation of cystometry of passive and of stimulated bladder. We hope that our consideration and new concept inspires us to do more basic research and related clinical investigations.
References
- Abstract
- Introduction
- Elastic Compliance CE, Elastic Volume VE and Rest Volume VR derived from Autonomous Expulsion of Accommodated Pig Bladders Ex-Vivo with Varied Initial Volume
- Summary of Published Experimental Results
- Mechanical Explanation
- Application of The Sliding Filaments Model
- Conclusion and Discussion
- References
- P Abrams, J G Blaivas, S L Stanton, J T Andersen (1988) I.C.S. The standardization of terminology of lower urinary tract function. The International Continence Society Committee on Standardization of Terminology. Scand J Urol Nephrol Suppl 114: 5-19.
- Wyndaele JJ, GammieA, Bruschini H, De Wachter S, Fry CH, et al. (2011) Bladder compliance what does it represent: can we measure it, and is it clinically relevant? Neurourol Urodyn 30(5): 714-722.
- Coolsaet B (1985) Bladder compliance and detrusor activity during the collection phase. Neurourol Urodyn 4(4): 263-273.
- Duyl WA van (2021) Biomechanics of urinary bladder: slow-filling and slow-emptying cystometry and accommodation. Bladder 8(1): e45.
- Mastrigt R van, Coolsaet BLRA, Duyl WA van (1978) Passive properties of the urinary bladder in the collection phase. Med Biol Eng Comput 16(5): 471-482.
- Griffiths DJ, Mastrigt R van, Duyl WA van, Coolsaet BLRA (1979) Active mechanical properties of the smooth muscle of the urinary bladder. Med Biol Eng Comp 17(3): 281-290.
- Duyl W.A. van (1985) A model for both the passive and active properties of urinary bladder tissue related to bladder function. Neurourol Urodyn 4(4): 275-283.
- Hill AV (1938) The heat of shortening and the dynamic constants of muscle. Pro R Soc Ser B 126(843): 136-195.
- Duyl WA van, Coolsaet BLRA (2021) Biomechanics of the urinary bladder: spontaneous contraction activity and micromotions related to accommodation. Int Urol Nephrol 53(7): 1345-1353.
- van Duyl WA, Coolsaet BLRA, Van Mastrigt R (1978) A new clinical parameter for the assessment of the contractility of the urinary bladder. Urol Int 33(1-3): 31-39.
- Mastrigt R van (1977) A systems approach to the passive properties of the urinary bladder in the collection phase. Thesis, Erasmus University Rotterdam, Netherlands.
- Ratz PH, Speich JE (2010) Evidence that actomyosin cross bridges contribute to “passive” tension in detrusor smooth muscle. Am J Physiol Renal Physiol 298(6): F1424-1435.
- Coolsaet BLRA, Mastrigt R van, Duyl WA van, Rees Vellinga F van (1978) Some influences of the contractile element on the visco-elastic properties of bladder wall strips. Eur Urol 4(6): 450-456.
- Mastrigt R van, Tauecchio EA (1982) Series-elastic properties of strips of smooth muscle from pig urinary bladder. Med Biol Eng Comput 20(5): 585-594.
- Mastrigt R van (1988) The length dependence of the series elasticity of pig bladder smooth muscle. J Muscle Res Cell Motil 9(6): 525-532.
- Duyl WA van (2021) Fundamental aspects of isovolumetric contractility measurements of urinary bladder: A Review. Recent developments in Medicine and Medical Research 4: 62-70.
- Duyl WA van (1985) Spontaneous contractions in urinary bladder smooth muscle: preliminary results. Neurourol Urodyn 4(4): 301-307.
- Huxley AF (1957) Muscle structure and theories of contraction. Prog Biophys Biophys Chem 7: 255-318.
- Warshaw DH, Fay FS (1983) Cross-bridge elasticity in single smooth muscle cells. J Gen Physiol 82(2): 157-199.
- Glerum JJ, Mastrigt R van, Koeveringe AJ van (1990) Mechanical properties of mammalian single smooth muscle cells. III. Passive properties of pig detrusor and human a terme uterus cells. J Muscle Res Cell Motil 11(5): 453-462.
- Murphy RA, Rembold CM (2005) The latch-bridge hypothesis of smooth muscle contraction. Can J Physiol Pharmacol 83(10): 857-864.
- Sugi H (1992) Muscle Contraction and Cell Motility. Advances in comparative and environmental physiology 12.
- Gosling JA, Dizon JS, Humpherson JR (1983) Functional anatomy of the urinary tract. London and New York Gower Medical Publishing 316-318.
- Tombe PP, Mateja RD, Kittipong-Tachampa, Younss Alt Mou, Farman GP, et al. (2010) Myofilament length dependent activation. J Mol Cell Cardiol 48(5): 851-858.
- Eddinger TJ (2017) Reversible plasticity of detrusor smooth muscle: evidence for a key role of “slipping” actomyosin cross-bridges in the control of urinary bladder compliance. Am J Physiol Renal Physiol 313(4): F862-F863.
- Colhoun AF, Klausner AP, Nagle AS, Carroll AW, Barbee RW, et al. (2017) A pilot study to measure dynamic elasticity of the bladder during urodynamics. Neurourol Urodyn 36(4): 1086-1090.
- Duval DLM, Weprin S, Nandanan N, Cullingsworth ZE, Balthazar A, Magino M, Speich JE, Klausner AP 2021: Regulation of bladder dynamic elasticity: a novel method to increase bladder capacity and reduce pressure using pulsatile external compressive exercises in a porcine model. Vol 53,July Int Urology and Nephrology DOI: 10.1007/s11255-021-02863-1

Top Editors
-

Mark E Smith
Bio chemistry
University of Texas Medical Branch, USA -

Lawrence A Presley
Department of Criminal Justice
Liberty University, USA -

Thomas W Miller
Department of Psychiatry
University of Kentucky, USA -

Gjumrakch Aliev
Department of Medicine
Gally International Biomedical Research & Consulting LLC, USA -

Christopher Bryant
Department of Urbanisation and Agricultural
Montreal university, USA -

Robert William Frare
Oral & Maxillofacial Pathology
New York University, USA -

Rudolph Modesto Navari
Gastroenterology and Hepatology
University of Alabama, UK -

Andrew Hague
Department of Medicine
Universities of Bradford, UK -

George Gregory Buttigieg
Maltese College of Obstetrics and Gynaecology, Europe -

Chen-Hsiung Yeh
Oncology
Circulogene Theranostics, England -
.png)
Emilio Bucio-Carrillo
Radiation Chemistry
National University of Mexico, USA -
.jpg)
Casey J Grenier
Analytical Chemistry
Wentworth Institute of Technology, USA -
Hany Atalah
Minimally Invasive Surgery
Mercer University school of Medicine, USA -

Abu-Hussein Muhamad
Pediatric Dentistry
University of Athens , Greece

The annual scholar awards from Lupine Publishers honor a selected number Read More...